机器学习算法：关联规则分析

公众号：尤而小屋
作者：Peter
编辑：Peter

大家好，我是Peter~

今天给大家分享一个经典的机器学习算法：关联规则分析，从理论到代码到实战，全部拉满。

本文主要内容：

文章过长，建议收藏

经典案例

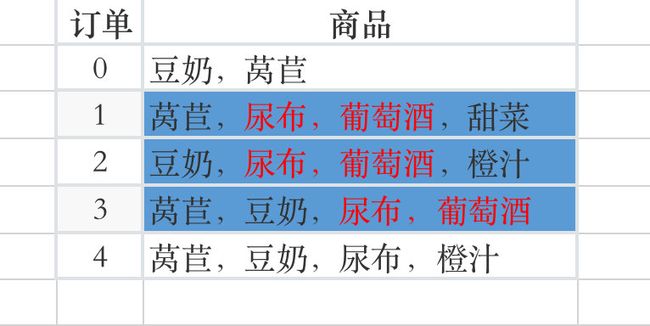
关联分析是一种从大规模的数据集中寻找有趣关系的方法。一个经常被用到关联分析的例子：购物篮分析。

通过查看哪些商品经常在一起被顾客购买，可以帮助商店去了解用户的购买行为。

经典的啤酒和尿布的案例：

某家超市的销售管理人员在分析销售订单时发现，啤酒与尿布这两件看起来毫不关联的商品竟然经常会出现在同一个订单中。

后来跟踪调查发现，原来年轻夫妇一般在周五晚上妻子会安排丈夫去超市购买尿布，而丈夫在购买尿布时总会忍不住顺便给自己买上几罐啤酒。

这就是为什么啤酒和尿布这两件看起来毫不关联的商品经常会出现在同一个购物篮中。

为了解决啤酒和尿布同时出现的问题，这样便引出了关联规则分析的算法。

关联规则如今还被用在许多应用领域中，包括网络用法挖掘、入侵检测、连续生产及生物信息学中。

相关术语

在利用关联规则（分析）的过程中，经常会遇到几个术语：

事务库

上面的商品购物的数据就是一个事务库，记录的每条数据。

事务

事务库中的每条记录称之为一笔事务。一笔事务就是一次购买行为。

k-项集

在上面的例子中，每个商品称之为一个“项”。项的集合称之为项集。比如**{尿布},{尿布,啤酒},{尿布,莴苣},{尿布,啤酒,莴苣}**等都是项集，也就是不同商品的组合。

含有k个项的项集称之为k-项集，1-项集，2-项集，….,k-项集

关联规则

关联规则association rules：暗示物品之间可能存在很强的关系，是形如$A—>B$的形式。

其中A称之为前件，B称之为后件，表示：如果用户购买了A商品，也会购买B商品。

在这里，AB可以是单一的商品，也可以是某个项集

比如：{A,B} —>{C}表示的就是如果用户购买了AB商品，那么也会购买C商品。

频繁项集

频繁项集frequent item sets：是指经常出现在一块的物品的集合。比如上面例子中的{尿布，葡萄酒}就是一个很好的例子。

支持度（下面）大于等于人为指定的阈值（这个阈值称之为最小支持度）的项集，称之为频繁项集。

假设最小支持度是50%，如果得到某个项集{啤酒，尿布}的支持度是70%（假定），我们把{啤酒，尿布}称之为频繁项集。

评估标准

关联规则中的评估指标有3个：

1. 支持度Support
2. 置信度Confidence
3. 提升度Lift

支持度

支持度Support：数据集中包含该项集的记录所占的比例。比如上面总共有5条记录，其中{尿布，葡萄酒}共有3条。因此{尿布，葡萄酒}的支持度就是3/5。

用公式可以表示为：

$$support(XY)=\frac{num(XY)}{num(samples)}$$

支持度是针对项集的。在实际的需求中，可以指定一个最小支持度，从而来保留满足最小支持度的项集，起到数据过滤的作用。

可信度/置信度

可信度/置信度 Confidence：是针对一条诸如{尿布}—>{葡萄酒}的关联规则来进行定义的。我们可以将可信度定义为：

支持度{尿布, 葡萄酒} / 支持度{尿布}

在上面的例子中：支持度{尿布, 葡萄酒} = 3/5；支持度{尿布}=4/5。那么：可信度就是(3/5) / (4/5) = 3/4=75%

这样的含义就是：在所有包含尿布的订单中，有75%的包含葡萄酒

如果用条件概率的公式可以表示为：

$$Confidence(X—>Y)=P(Y|X)=\frac{P(XY)}{P(X)}$$

也就是：在X发生的条件下Y发生的概率 = XY同时发生的概率 / X发生的概率

在上面的例子中，假定有一条关联规则**{尿布,啤酒} —>{莴苣}**可以表示为：

$$P(莴苣|(尿布,啤酒))=\frac{P(莴苣,啤酒,尿布)}{P(尿布,啤酒)}$$

提升度

提升度Lift表示含有X的条件下，同时含有Y的概率，与Y总体发生的概率之比。也就是X对Y的置信度与Y总体发生的概率之比：

$$Lift(X—>Y)=\frac{P(Y|X)}{P(Y)}=\frac{Confidence(X—>Y)}{P(Y)}$$

提升度反映了关联规则中的X与Y的相关性强弱

• 提升度>1且越高表明正相关性越高
• 提升度<1且越低表明负相关性越高
• 提升度=1表明没有相关性

强关联规则

一个重要的概念：强关联规则。在实际的应用中，通常是：

1. 先寻找满足最小支持度的频繁项集
2. 然后在频繁项集中寻找满足最小置信度的关联规则

这样找出来的关联规则称之为强关联规则。

案例

通过一个简单的例子来理解3个指标。假定一个班级40个同学，男女各20个，统计他们对篮球和乒乓球的兴趣：

性别	篮球	乒乓球
男（共20人）	18	20
女（共20人）	0	12

假定：X = {喜欢篮球}，Y={喜欢乒乓球}，求出**关联规则{X—>Y}（既喜欢篮球，又喜欢乒乓球）**3个指标

1、针对男生

Support{X,Y}=18/20   # 18个人同时喜欢；20是男生总数
Confidence{X,Y}=P(Y|X)=P(XY)/P(X)=18/18=1 # 第一个18：表示同时喜欢的人数，第二个表示喜欢篮球人数
Lift{X,Y}=Confidence{X,Y} / P(Y)=1/1=1

此时提升度为1，说明XY是相互独立，彼此互不影响。也就是说，在男生中喜欢篮球和乒乓球没有任何关联。

虽然支持度和可信度都挺高的，但它们也不是一条强关联的规则。

2、针对女生

Support{X,Y}=0/20=0  # 没有女生喜欢篮球
Confidence{X,Y}=P(Y|X)=P(XY)/P(X) = 0
Lift{X,Y}=0

在女生中完全没有任何关联

3、针对整体

Support{X,Y}=18/40=9/20
Confidence{X,Y}=P(Y|X)=P(XY)/P(X)=(18/40) / (18/40)=1
Lift{X,Y}=Confidence{X,Y}/P(Y) = 1 / (32/40)=5/4

在整体中支持度和可信度都挺高，而且提升度也大于1，说明XY是强关联的规则。

Apriori算法

关联分析的最终目标是找出强关联规则。Apriori算法是著名的关联规则挖掘算法之一。算法的主要步骤：

1. 设定最小支持度和最小置信度
2. 根据最小支持度找出所有的频繁项集
3. 根据最小的置信度发现强关联规则

商品组合

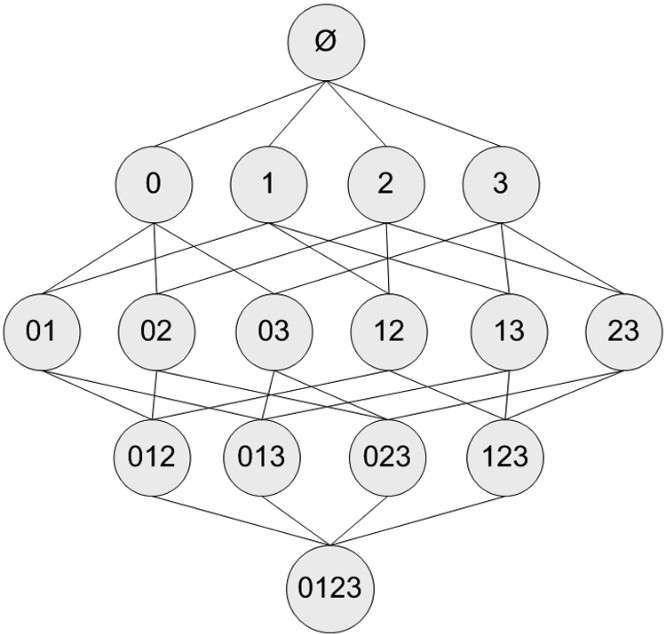
假设有4种商品：商品0、商品1、商品2、商品3。可以快速理清被一起购买的商品组合。比如0号商品：

• 单独被购买
• 和某商品一起：01、02、03
• 和2种商品一起：012、013、023
• 和3种商品一起：0123

注释：第一个集合是$\varphi$。表示的是空集或者不包含物品的集合

支持度计算

某个集合的支持度：是指有多少比例的交易记录包含了该集合。比如{0,3}集合的支持度的计算：

• 遍历每个记录检查是否包含{0,3}。如果包含记录数加1
• 在遍历完全部数据之后，使用得到的支持度为：包含集合的总记录数 / 总的交易记录数

上面的例子中，仅有4种商品，从【项集组合图】中我们看到：需要遍历15次。当有N个商品，遍历的次数就是$2^N-1$次。

数据量会剧增，计算时间随之大量增加。为了解决这个问题，Apriori算法来了。

算法假设：如果某个项集是频繁的，那么包含它的所有子集也是频繁的。

浅理解下：如果项集{1,3}是频繁的，那么{1}或者{3}也是频繁的。也就是说：如果某个项集是非频繁项集，那么它的所有超集都是非频繁项集。

在下图中灰色表示的非频繁项集。如果**{2,3}是非频繁项集**，那么它的超集{023}、{123}、{0123}都是非频繁项集。

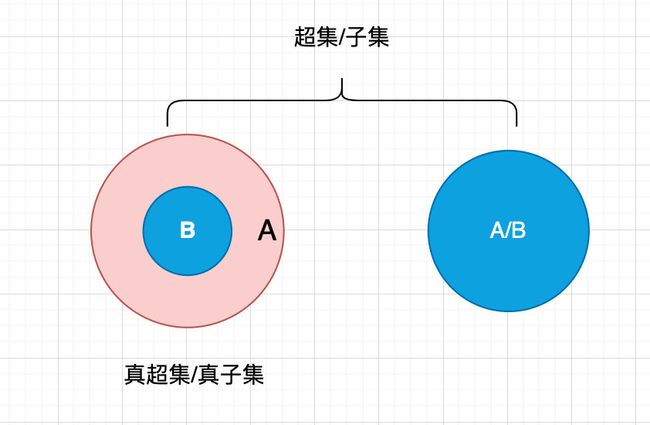
关于超集和子集

如果集合A包含集合B中的全部元素，且集合A可能存在集合B中不存在的元素，那么集合A就是集合B的超集，反之集合B就是就是集合A的超集。

如果集合A中一定存在集合B中不存在的元素，那么A就是B的真超集，反之B是A的真子集。

算法流程

1. 给定一份数据或者模拟一份数据集dataSet
2. 从原始数据集中创建C1（只含有一个元素的项集）
3. 通过scan函数来扫描数据，找到满足大于最小支持度的频繁项集L1
4. 将L1中的每个1-项集进行两两组合，重复步骤3，找到频繁项集L2
5. 重复步骤3,4直到k-项集循环完为止

• C1到Ck代表1-项集，k-项集
• L1到Lk代表的是含有k个数据集的频繁项集
• scan方法：扫描整个数据集。对数据进行过滤，去除那些不满足最小支持度的数据

生成候选项集

1、模拟数据

def loadData():
    """
    模拟需要的数据
    """
    dataSet = [[1,3,4],[2,3,5],[1,2,3,5],[2,5]]
    return dataSet

2、生成基于单个元素的项集

必须使用frozenset，后续作为字典的键

def createC1(data):
    """
    功能：生成第一个候选数据集C1
    参数：原始数据集dataset
    返回：frozenset形式的候选集合C1
    """
    
    C1 = []
    for transaction in data:  # 遍历data的每条元素，比如：[1,3,4] 当做一个元素
        print(transaction)
        for item in transaction:  # 遍历data元素中的每个元素，比如：1,3,4,2,3,5...
            print(item)
            if not [item] in C1:  # 单个元素当做列表追加到C1中 [item]是为每个物品构建一个集合
                C1.append([item])
                print(C1)
                
    C1.sort()   # [[1], [2], [3], [4], [5]]
    return list(map(frozenset, C1))  # 对C1中的每个元素执行frozenset函数的功能

在生成C1的过程中，如果某个元素已经在其中，则大列表中不会在进行添加。

3、生成候选项集

def scanD(D, Ck, minSupport):
    """
    参数：
        D：传入数据dataset
        Ck：候选集列表
        最小支持度
    """
    ssCnt = {}
    for tid in D:  # 遍历原始数据
        for can in Ck:  # 遍历k项集中的每个数据
            if can.issubset(tid):  # 判断can是否是tid的子集，返回的是布尔类型数据
                if can not in ssCnt.keys():  # 如果不在ssCnt的key里面，就赋值为1
                    ssCnt[can] = 1
                else:  # 否则再加1
                    ssCnt[can] += 1  
                    
    numItems = float(len(D))  # 数据集的长度
    retList = []  # 频繁项集
    supportData = {}  # 存放候选项集Ck的支持度字典：key-候选项  value-支持度
    
    for key in ssCnt:  # 对key进行遍历
        support = ssCnt[key] / numItems  # 取出key对应的支持度
        supportData[key] = support  # 存放候选项集的支持度
        if support >= minSupport:  # 判断如果大于最小支持度就追加到列表中
            retList.append(key)
    return retList, supportData  # 频繁项集 候选项集

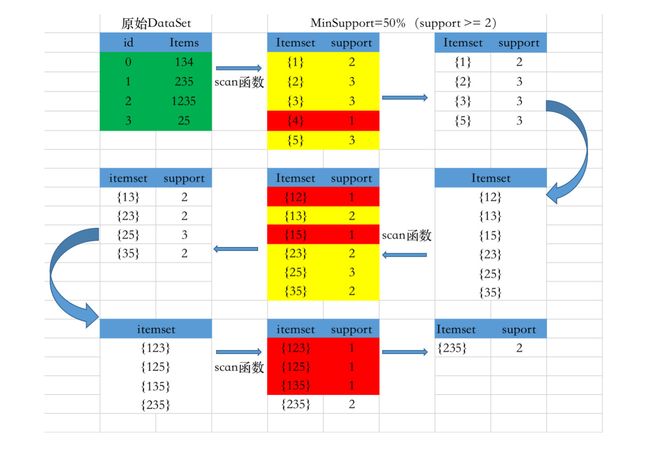
其中{4}项集的置信度小于阈值0.5，直接被舍弃了。

生成频繁项集

算法的伪代码：

当集合中项的个数大于0时:
  构建一个k个项组成的候选项集的列表
  检查数据以确认每个项集都是频繁的
  保留频繁项集并构建k+1项组成的候选项集的列表

def aprioriGen(Lk,k):
    """
    功能：生成频繁项集
    参数：
        Lk：包含k个元素的频繁项集
        k：项集的元素个数
    返回：
        Ck：候选项集列表
    """
    
    Ck = []  # 频繁项集，比如 {0、1}{0、2}和{1、2}
    length = len(Lk)  # 项集的数量，上面例子的话就是3
    
    for i in range(length):  
        for j in range(i+1, length):  
            # 前k-2个项集相同的话，就将两个集合合并，得到k的元素的集合
            L1 = list(Lk[i])[:k-2]
            L2 = list(Lk[j])[:k-2]
            L1.sort()  # 排序操作
            L2.sort()
            
            if L1==L2:
                Ck.append(Lk[i] | Lk[j])  # 合并
                
    return Ck  # 候选项集列表

关于上述代码中k-2的解释：

1. 假如我们利用{0}、{1}、{2}，可以快速构建{0、1}{0、2}和{1、2}
2. 当使用{0、1}、{0、2}和{1、2}来构建{0、1、2}的时候，如果我们将集合两两合并，就会得到{0、1、2}、{0、1、2}、{0、1、2}，也就是说数据是重读了三次。
3. 当接下来扫描3个元素的项集列表来得到非重复结果，需要确保遍历列表的次数最少。如果比较集合{0、1}{0、2}和{1、2}的第一个元素，并且只对第一个元素相同的进行合并操作，就可以得到集合{0、1、2}

再看二项集生成三项集的例子，假如有多个二项集的元素：{0,1}、{0,2}、{0,3}、{1,2}、{1,3}、{2,3}。

最终合成后是：{0,1,2}、{0,1,3}、{0,2,3}、{1,2,3}。其中{1,2,3}是最先由{1,2}、{1,3}生成的，且重复元素还在第一位，而不是{1,3}、{2,3}

类推下，如果是3项集生成4项集的话，就是首2位相同；生成n项集的就是前面的0到k-2位元素相同

aprioriGen(L1, 2)   # 调用函数

[frozenset({1, 3}),
 frozenset({1, 2}),
 frozenset({1, 5}),
 frozenset({2, 3}),
 frozenset({3, 5}),
 frozenset({2, 5})]

主函数

def apriori(D, minSupport=0.5):
    """
    功能：主函数
    函数：
        D：原数据
        minSupport：支持度
    返回值：
        L：频繁项集
        supportData：支持度数据
    """
    C1 = createC1(D)  # 先生成C1候选项集
    L1, support = scanD(D, C1, minSupport)  # 扫描原始数据，找出满足minSupport的数据
    L = [L1]
    k = 2
    
    while (len(L[k-2]) > 0):
        Ck = aprioriGen(L[k-2], k)
        Lk, supK = scanD(D, Ck, minSupport)
        supportData.update(supK)
        L.append(Lk)
        k += 1
    return L, supportData

运行下主函数

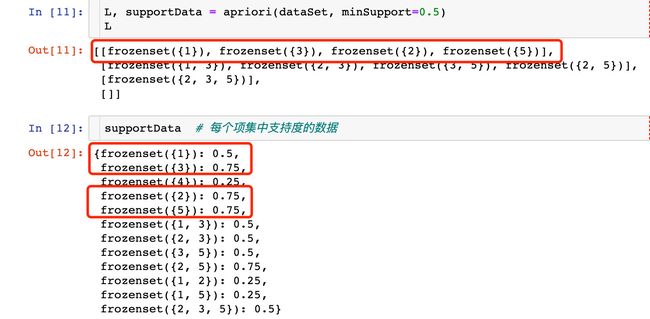
L, supportData = apriori(dataSet, minSupport=0.5)

结论：当minsupport=0.5的时候，我们可以看到1-项集中满足条件的数据

改变支持度的效果：

apriori(dataSet, minSupport=0.7)

([[frozenset({3}), frozenset({2}), frozenset({5})], [frozenset({2, 5})], []],
 {frozenset({1}): 0.5,
  frozenset({3}): 0.75,
  frozenset({4}): 0.25,
  frozenset({2}): 0.75,
  frozenset({5}): 0.75,
  frozenset({1, 3}): 0.5,
  frozenset({2, 3}): 0.5,
  frozenset({3, 5}): 0.5,
  frozenset({2, 5}): 0.75,
  frozenset({1, 2}): 0.25,
  frozenset({1, 5}): 0.25,
  frozenset({2, 3, 5}): 0.5})

流程

1. 首先从原始数据中经过扫描函数得到1-项集和相应的置信度；选择满足置信度大于等于0.5，也就是support>=2的频繁项集（右侧拐弯的大箭头）
2. 然后将1-项集进行两两组合，得到2-项集。再次经过扫描函数，对原始数据再次进行扫描，查看2-项集中每个元素的置信度，找出选择满足置信度大于等于0.5的频繁项集（左侧拐弯的大箭头）
3. 将2-项集中的数据两两组合，得到3-项集中的每个元素，对原始数据再次进行扫描，查看3-项集中每个元素的置信度，最后找到只有{235}满足

参考书籍

1. 《机器学习实战》
2. 《关联分析算法（Association Analysis）Apriori算法和FP-growth算法初探》