leetcode每天5题-Day11

1.多数元素

leetcode169. 多数元素-简单
给定一个大小为 n 的数组 nums ，返回其中的多数元素。多数元素是指在数组中出现次数 大于 ⌊ n/2 ⌋ 的元素。
你可以假设数组是非空的，并且给定的数组总是存在多数元素。
①Map
数字为key，重复次数为value

var majorityElement = function(nums) {
const n=nums.length;
if(n==1) return nums[0];
const little=Math.floor(n/2);

const map=new Map();
for(const num of nums){
    if(!map.get(num)){
        map.set(num,1);
    }else{
        map.set(num,map.get(num)+1);
        if(map.get(num)>little){
            return num;
        }
    }
    
}
};

②排序
如果将数组 nums 中的所有元素按照单调递增或单调递减的顺序排序，那么下标为⌊2/n⌋ 的元素（下标从 0 开始）一定是众数。

var majorityElement = function(nums) {
    nums.sort((a,b)=>a-b);
    return nums[Math.floor(nums.length/2)];
};

时间复杂度：O(nlogn)。将数组排序的时间复杂度为O(nlogn)。
空间复杂度：O(logn)。如果使用语言自带的排序算法，需要使用O(logn)的栈空间。如果自己编写堆排序，则只需要使用O(1)的额外空间。
③分治
④Boyer-Moore 投票算法

2.2 的幂

leetcode231. 2 的幂-简单
给你一个整数 n，请你判断该整数是否是 2 的幂次方。如果是，返回 true ；否则，返回 false 。
如果存在一个整数 x 使得 n == 2的x次方 ，则认为 n 是 2 的幂次方。
①循环

var isPowerOfTwo = function(n) {
    if(n==0) return false;
    if(n==1) return true;
    while(n>=2){
        n=n/2;
    }
    if(n==1){
            return true;
        }else{
            return false;
        }
};

进阶：你能够不使用循环/递归解决此问题吗？
②二进制表示
将n的二进制表示中的最低位中的1提取出来，再判断剩余数值是否为0。
两种常见的与二进制表示中最低位相关的位运算技巧：

1. n&(n-1)—>将最低位1移除

var isPowerOfTwo = function(n) {
   return n > 0 && (n & (n - 1)) === 0;
};

2. n&(-n)—>获取最低位的1
   由于负数是按照补码规则在计算机中存储的，-n的二进制表示为n的二进制表示的每一位取反再加上1。
   如果n是正整数并且n & (-n) = n，那么n就是2的幂

var isPowerOfTwo = function(n) {
    return n > 0 && (n & -n) === n;
};

时间复杂度：O(1)。
空间复杂度：O(1)。

③判断是否为最大2的幂的约数
取巧做法：在题目给定的32位有符号整数的范围内，最大的2的幂为 2^{30} = 10737418242 。我们只需要判断n是否是 2^{30}的约数即可。

var isPowerOfTwo = function(n) {
    const BIG = 1 << 30;
    return n > 0 && BIG % n === 0;
};

时间复杂度：O(1)。
空间复杂度：O(1)。

3.二叉搜索树的最近公共祖先

leetcode235.二叉搜索树的最近公共祖先-简单
给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。
①非递归解决
根据p、q值的大小与根节点值的大小，如果p和q分别在r两侧，那么r就是答案。

var lowestCommonAncestor = function(root, p, q) {
    // q p 在同一侧
    while((root.val-p.val)*(root.val-q.val)>0){
        root=p.val>root.val?root.right:root.left;
    }
    return root;
};

4.最小时间差

leetcode539. 最小时间差-中等
题目：给定一个 24 小时制（小时:分钟 “HH:MM”）的时间列表，找出列表中任意两个时间的最小时间差并以分钟数表示。
①排序
排序后，最小时间差必然出现在相邻的两个时间或首尾时间中。
chatCodeAt()：返回指定位置的字符的 Unicode 编码

var findMinDifference = function(timePoints) {
    timePoints.sort();
    let ans=Number.MAX_VALUE;
    let t0Time=getMinutes(timePoints[0]);
    let preTime=t0Time;
    for(let i=1;i<timePoints.length;i++){
        const minutes=getMinutes(timePoints[i]);
        ans=Math.min(ans,minutes-preTime);
        preTime=minutes;
    }
    ans=Math.min(ans,t0Time+1440-preTime);
    return ans;
};
const getMinutes=(t)=>{
    return ((t[0].charCodeAt()-'0'.charCodeAt())*10+(t[1].charCodeAt()-'0'.charCodeAt()))*60+(t[3].charCodeAt()-'0'.charCodeAt())*10+(t[4].charCodeAt()-'0'.charCodeAt())
}

时间复杂度：O(nlogn)，其中n是数组timePoints的长度。排序需要O(nlogn)的时间。
空间复杂度：O(n)或O(logn)。为排序需要的空间，取决于具体语言的实现。

substring和substr的区别

var findMinDifference = function(timePoints) {
    // 把数组里的每一项转为分钟
    const timeArray=timePoints.map(item=>{
        return item=parseInt(item.substr(0,2))*60+parseInt(item.substr(3,2));
    }).sort((a,b)=>a-b);
    const numList=[];
    timeArray.forEach((item,i)=>{
        if(i>0){
            numList.push(Math.min(Math.abs(timeArray[i]-timeArray[i-1]),1440-Math.abs(timeArray[i]-timeArray[i-1])));
        }
    })
    const lastTime=Math.abs(timeArray[timeArray.length-1]-timeArray[0]);
    numList.push(Math.min(lastTime,1440-lastTime));
    numList.sort((a,b)=>a-b);
    return numList[0];
};

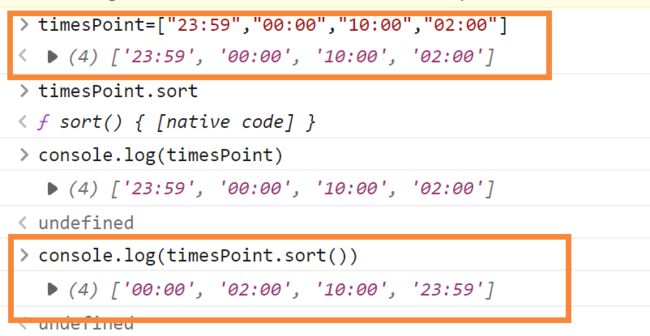
注意： 排序这里有个坑，对于字符串数组，即该题中的timePoints，可以直接用sort()排序。但对于数值型的数组，要写成Array.sort((a,b)=>a-b)的形式，因为Js是弱类型语言，它看不出里面int类型的数字。

字符串数组排序成功：

数值型数组(sort()是原地排序，不生成新数组)：

关于undefined：在浏览器里面的脚本代码段里面写一条语句为什么会在输出结果后面显示一个undefined

②鸽巢原理
根据题意，一共有24×60=1440种不同的时间。由鸽巢原理可知，如果timePoints的长度超过1440，那么必然会有两个相同的时间，此时可以直接返回0。

const n = timePoints.length;
    if (n > 1440) {
        return 0;
    }

5.数组的最小偏移量

leetcode1675. 数组的最小偏移量-困难

①有序队列
一个数的变化范围有限, 比如所有的奇数都只能做一次乘 2 操作, 偶数可以做若干次除以 2 的操作.
把所有数都变成自己可变化范围的最大值. （即所有奇数都乘2），然后再缩小范围
而偏移量 = 最大值 - 最小值, 所以我们要做的就是缩小最大值. (缩小其他数值也无法优化偏移量)
那么操作就是: 不断缩小当前的最大值即可, 直到不能缩小, 期间不断维护答案.
这里可以使用有序队列来维护一个有序的数组，slist[0]为最小值，slist[-1]为最大值。

class Solution:
    def minimumDeviation(self, nums: List[int]) -> int:
            from sortedcontainers import SortedList
            slist=SortedList()
            for num in nums:
                if num%2:slist.add(num*2)
                else:slist.add(num)
            ans=slist[-1]-slist[0]
            while slist[-1]%2==0:
                MAX=slist.pop()
                slist.add(MAX//2)
                ans=min(slist[-1]-slist[0],ans)
            return ans;

参考这篇
②最大堆