Android 网络编程之HTTPS详解
前言:HTTPS涉及相关的知识,总是很难的将其归纳总结起来,本文旨在带你学习详细的HTTPS相关知识点,看完本文后,你会了解到以下相关知识点;
- HTTPS的工作原理
- HTTPS为什么要这样设计
- 密码学相关原理
那么接下来让我们开启HTTPS的学习之旅吧!
本章目录
- 1、HTTPS是什么?
- 2、什么是加密?
- 3、什么是对称加密?
- 4、什么是非对称加密?
- 5、数字证书
- 6、什么是SSL/TSL?
本章结构图
1、HTTPS是什么?
1.1、HTTPS的介绍
HTTPS简称:超文本传输安全协议(英语:HyperText Transfer Protocol Secure,缩写:HTTPS);
乍一看,好像和HTTP没啥区别,但是仔细一看,多了安全两个字,这表示啥呢?
表示HTTPS是安全的超文本传输协议,那么它和HTTP有啥关系呢?因为这两看着确实太像了;
没错,它两确实有关系,HTTPS是基于HTTP协议,通过一些方式(下面会讲)来进行数据的安全传输,我们知道HTTP的传输是不安全的,而HTTPS解决了这个问题;
HTTPS协议发明出来的主要目的就是保护互联网的传输过程中,保护数据的隐私和完整性,最开始是由网景公司(Netscape)在1994年首次提出的协议,后来就扩展到互联网上了;
那么接下来让我们来继续深入了解吧;
1.2、HTTP的痛点
HTTP协议,是我们目前使用最多,也是最广泛的协议,几乎我们无时无刻不在使用着它,但是HTTP有一个致命的缺点,就是不能进行安全的传输;
网络的世界是很复杂的,如果有人想要窃取或者篡改某些你要传输的数据,那么在HTTP协议上是很容易出现的,比如登录、转账这些极其敏感的操作,如果不使用安全的传输协议,那么就很容易被不法分子所利用,导致损失惨重;
那么安全的传输协议也是必不可少了;
1.3、HTTPS是怎么工作的?
HTTPS是基于HTTP的基础上进行工作的,通过加密协议对通信进行加密,该协议称之为传输层安全性(TLS),以前是被称作为SSL;
该协议通过非对称加密的方式来对通信进行加密,通信的双方使用不同的公钥和私钥,以此来保证数据传输的安全性;
私钥:为客户端或者浏览器端所持有,不为外部得知,用于解密公钥加密的信息;
公钥:为公开的秘钥,所有人都可以持有公钥,用公钥加密的数据,只有私钥才可以解开;
1.4、HTTPS可以被抓包吗?
那么HTTPS是具有安全性的通信协议,那么HTTPS可以被抓包吗?
答案是:无法避免被别人抓包;
我们先来看看抓包的原理,其中一个为代理模式,也就是中间人;
中间人:在客户端和服务端中间有一个中转站,对于客户端来说,伪造成服务端,对于服务端来说,伪造成客户端,这种就造成了数据的传输都会经过这个中转站,从而被获取到;
这个我们下面再讲,我们这里结论先行;
如果感兴趣的请参考:为什么使用了https还是可以被抓包
2、什么是加密?
2.1、加密
将内容转换为无法识别的密文,这个过程就叫做加密;
比如有一串中文:我是祖国的花朵。
那么加密后可能就变成:HSUUI&&*768SASKD&7980%8SHOS%^$hUSHHD&6788
那么上面的那一串密文是无法直接读取过来的,必须要通过解密后,才可以看到内容;
而加密的方式有很多,这里就先讲讲几种主要使用的加密方式;
2.2、哈希
哈希算法是不可逆加密算法;
为啥叫不可逆呢?
因为加密后的内容是无法被转化为原来的内容的,那么到这里你是否会有疑问?
既然加密后不能转化为原来的内容,那么这个加密还有什么用呢?
不可逆加密的用途,大多都是用于数据校验,不可逆加密算法有一个很大的特点就是,和原内容强相关,什么意思呢?
就是说原内容,经过不可逆算法生成的值,是和原内容息息相关的,如果原内容被篡改了一个字符或者几个字符时,生成的值就和原来的大不相同了;
所以这种特点非常适合于传输过程中的数据校验,判断数据在传输过程中是否被篡改了;
但是并不能避免数据被篡改,只是可以洞察到这种被篡改的情况;
3、对称加密
3.1、什么是对称加密
对称加密,简而言之就是解密和解密使用的秘钥是一致的;
也就是说使用对称加密的双方,都持有相同的秘钥,用于加密和解密;
下面我们从一张图里可以形象的看出对称加密算法加密解密的流程;
对称加密中,有几种常见的数学算法,目的是为了让被加密的数据尽可能的复杂,避免被很容易的破解,那么常用的数学算法有哪些呢?
3.2、对称加密涉及的数学计算有哪些?
(1) 移位和循环移位
移位就是数码按照一定的顺序进行移动,比如有一段数码为12345678,那么其右移后变成23456781,左移后变成81234567;
(2)置换
将数码中的数据根据置换表,进行移位,移动后的数据会变得杂乱无章;
比如一段置换表为:2,4,1,5,3,6; 那么123456这个数据根据这个置换表,进行置换后,数据就变成了:315246;
当然我这里只是举例,实际的置换表有64位,远远比这个复杂;
(3)扩展
将数码中的数据扩展为比原来更长的数据,可以利用置换表进行扩展;
(4)压缩
将数码中的数据压缩为比原来更短的数据,同理可以利用置换表进行压缩;
(5)异或
为二进制布尔代数运算
(6)迭代
进行多次重复的运算,这在加密算法里很常见,可以让数据变得更复杂和更难以破解;
3.3、DES算法的工作原理
下面我们来分析一下最常见的对称加密算法DES,以及其对应的工作原理;
(1):DES描述
DES算法全称为Data Encryption Standard,即数据加密算法,是IBM公司研发出来的对称加密算法,DES算法是典型的分组加密算法,也是应用最广泛的对称加密算法;
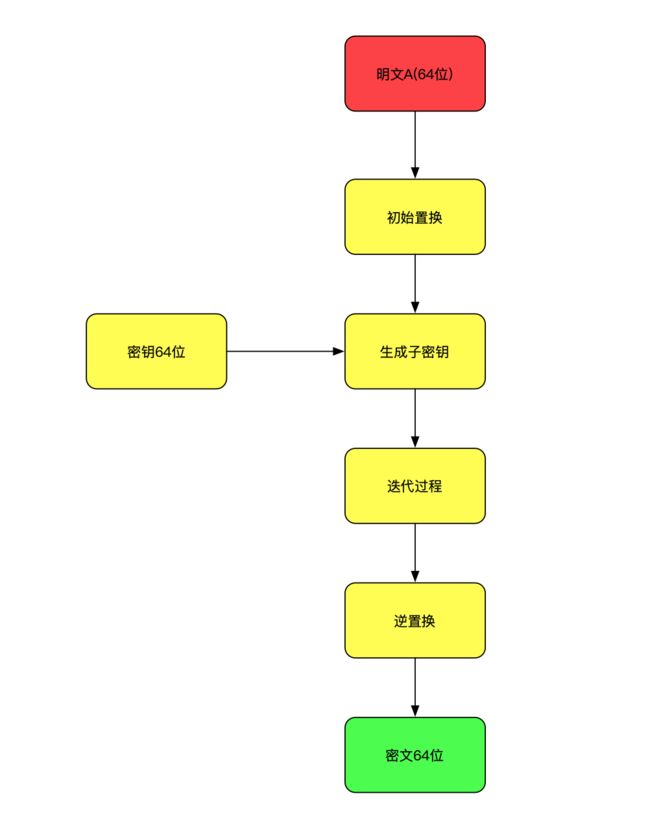
(2):DES工作原理
先来看一张流程图:
这里涉及太多复杂的操作,一时半会讲不完,这里就先缩略了,感兴趣的可以看看这位大佬写的文章:算法科普:神秘的 DES 加密算法
DES非对称加密算法是最为常见的分组加密算法,其核心在于置换与移位的数学运算,由于其加密算法是公开的,那么密钥的保密就非常的关键了,只要密钥泄露了,那么数据就会轻而易举的被破解了;
4、非对称加密
4.1、非对称加密是什么?
非对称加密,理解起来很简单,就是加密和解密的密钥不一样,正如这个名称所说的非对称;
下面我们以RSA非对称加密来举例;
非对称加密有两组密钥,一组为公钥,一组为私钥,这里为啥要组来称呼呢? 这个与非对称加密的原理有关,请继续往下看!
非对称加密的密钥格式为(a,b),a和b可以为任何整数,比如公钥(1234,12),私钥(1234,34)这种;当然我这里只是举例,这里的公钥和私钥没有关联关系;
上面为啥要说我这里随便写的没有关联关系呢?因为公钥和私钥是一一对应的,也就是说用公钥加密的,只能用对应的私钥才能解开;
那么到这里你是否有疑问了,为什么非对称的加密和解密的秘钥不一致?而不和对称加密一样,通过算法可以加密和解密内容;
4.2、RSA非对称加密算法
下面我们来讲讲RSA的加密和解密算法;
假设我们加密的公钥为(n,e);
加密算法:
$ m^e $ ≡ ≡ ≡ $ c$ ($ mod $ $ n$ )
RSA的加密算法为上面这个公式,所谓的加密,就是求这个公式的c,这里的m表示明文;
这个公式的解读:m的e次方除以n的余数为c,求c的值;
假如我们的明文m为12,公钥为(3233, 17);
那么代入公式后: $12^{17} $ ≡ ≡ ≡ c c c ( m o d mod mod 3233 3233 3233)
那么得到的结果c为:1730,那么1739就是用公钥加密后的结果;
接下来来看看解密算法;
假设我们解密的私钥为(n, d);
解密算法:
c d c^d cd ≡ ≡ ≡ m m m ( m o d mod mod n n n )
RSA的解密算法为上面这个公式,所谓的解密,就是求这个公式的m,这里的c表示密文;
这个公式的解读:c的d次方除以n的余数为m,求m的值;
这里解密的私钥为(3233,2753),经过公钥加密后的密文c为:1730;
那么代入公式后:$1730^{2753} $ ≡ ≡ ≡ m m m ( m o d mod mod 3233 3233 3233)
那么得到的结果为:12;
到这里RSA的加密解密算法就讲完了,RSA的加密解密和对称加密算法DES还不一样,没有DES的操作那么复杂,各种对数据进行置换,迭代,逆置换之类的,RSA的加密解密就是简单粗暴的进行n次方计算,最后求余数;
这里只是举了两个简单的密钥,而实际上的密钥不可能这么短,目前已有公开的破解的是768位,比较安全的是1024位,超级安全的是2048位;
那么到这里你是否已经明白,为什么RSA非对称加密算法相对对称加密算法会比较耗时呢?
这是因为RSA算法的加密解密都会进行多次的平方,密钥越长,那么经过的平方也就越多,因此会导致运算变慢;
4.3、RAS非对称加密算法的原理
上面我们讲了RSA非对称加密和解密算法,那么你是否会有疑问?
两组不相同的秘钥,通过不同的算法确认将明文加密后,正常解密为原来的明文,这是怎么做到的呢?那么让我们带着疑问继续看下去;
在开始之前,我们先来讲讲非对称加密涉及的数学原理;
1. 互质关系
什么是互质关系呢?
解读:如果两个正整数,除了1以外,没有其他公因子,我们就称这两个数是互质关系(coprime);
比如15和11,24和19,这个关系相信理解起来并不难;
2. 欧拉函数
什么是欧拉函数?
请思考一个问题:给出一个正整数,求小于这个正整数的互质数有多少个?
上面这个问题的求证过程就是欧拉函数,欧拉函数是用于求小于某个数的互质数的个数,用 φ ( n ) φ(n) φ(n)来表示;
比如 φ ( 10 ) = 5 φ(10) = 5 φ(10)=5 ,表示10的互质数分别有:9,7,5,3,1,那么加起来就为5个;
3. 欧拉定理
欧拉定理指的是:如果有两个整数a和b互质,那么下面的公式就会成立;
a φ ( b ) a^{φ (b)} aφ(b) ≡ ≡ ≡ 1 1 1 ( m o d mod mod b b b )
解读:a的 φ ( b ) φ (b) φ(b)次方除以b的余数为1; φ ( b ) φ (b) φ(b)就是欧拉函数;
对于欧拉定理的证明比较复杂,这么我们就不过多深入了,以免跑题;
4. 模反元素
模反元素指的是:如果两个正整数a和b互质,那么一定可以找到整数k,使得 ak-1 被b整除,或者说ak被b除的余数是1。
公式为:$ ak $ ≡ ≡ ≡ $ 1$ ($ mod $ $ b$ )
欧拉定理可以用来证明上面的公式必然成立;
如: a a a × \times × a φ ( b ) − 1 a^{φ (b) -1 } aφ(b)−1 ≡ ≡ ≡ 1 1 1 ( m o d mod mod b b b )
那么到这里,涉及的数学知识就讲完了,接下来我们就来讲讲非对称加密的公钥和私钥是怎么生成的;
密钥生成步骤:
第一步:随机选择两个互质数p和q;
第二步:将这两个质数想相乘,那么得到的结果为n;
第三步:求这个结果的欧拉函数,也就是 φ ( n ) = ( p − 1 ) ( q − 1 ) φ (n) = (p-1)(q-1) φ(n)=(p−1)(q−1)
第四步:随机选择一个整数e,e要大于1且小于 φ ( n ) φ (n) φ(n);
第五步:计算e对于于 φ ( n ) φ (n) φ(n)的模反元素d,也就是求公式:$ ed $ ≡ ≡ ≡ $ 1$ ($ mod $ $ φ (n)$ );
最终我们有了六个数据,分别为:p,q,n, φ ( n ) φ (n) φ(n),e,d;
这里将n和d封装成公钥(n,e),然后将n和d封装成私钥(n,d),当然这里只是举例,实际情况是用ASN.1格式来表示的;
接下来我们来看看RSA非对称加密的安全性,由上面生成的密钥可知,对外公布的公钥为(n,e),那么我们能不能在已知公钥的情况下,推导出私钥呢?
已知n,要解出d的值;
根据上面的步骤五的公式,$ ed $ ≡ ≡ ≡ $ 1$ ($ mod $ $ φ (n)$ ) ,要求出d的值就得先知道 φ ( n ) φ (n) φ(n)和e的值,才能求出来;
而根据上面的步骤三的公式, φ ( n ) = ( p − 1 ) ( q − 1 ) φ (n) = (p-1)(q-1) φ(n)=(p−1)(q−1), φ ( n ) φ (n) φ(n)的值得先知道p和q才能求出来;
而要求出p和q的值,就得对n做因数分解,但是对于大整数的分解是极其困难的,目前公布的被破解的RSA密钥最长为768位,而1024位的是比较安全的,2048位是极其安全,4096位是变态安全;
对于私钥解密公式的证明,这里就不过多深入探究了,感兴趣的请看这位巨佬写的两篇文章,超级详细;
RSA算法原理(一)
RSA算法原理(二)
5、数字证书
5.1、什么是数字签名?
刚看完非对称加密,接下来我们来看看数字签名;
在看下去之前,我们来思考一个问题,在通信的双方,如果发生了第三方攻击,也就是有黑客截取了主机A发送给主机B的数据,并且进行篡改后,在发送给主机B,而这时候主机B拿到的已经不是主机A发过去的原始数据了,数据已经被篡改了,那么我们怎么避免这种情况发生呢?
答案是:数字签名
那么这里可能会有疑问了?我使用非对称加密不就行了吗,第三方就算截取了我的数据,但是还是解密不了;
没错,非对称加密虽然可以防止被破解,但是还是不能防止被篡改,要是攻击者,把截取到的密文,修改了几个字符,那么接收者通过私钥解密后的内容就已经不是原来的内容了,所以这种方案还是不严谨;
我们先来看一下什么是数字签名?
数字签名其实就相当于人类的签名,数字签名就是通信的时候对数据进行签名,签名的作用就是通信的双方可以辨识该数据的身份,以免被伪造身份;
那么数字签名是怎么实现的呢?
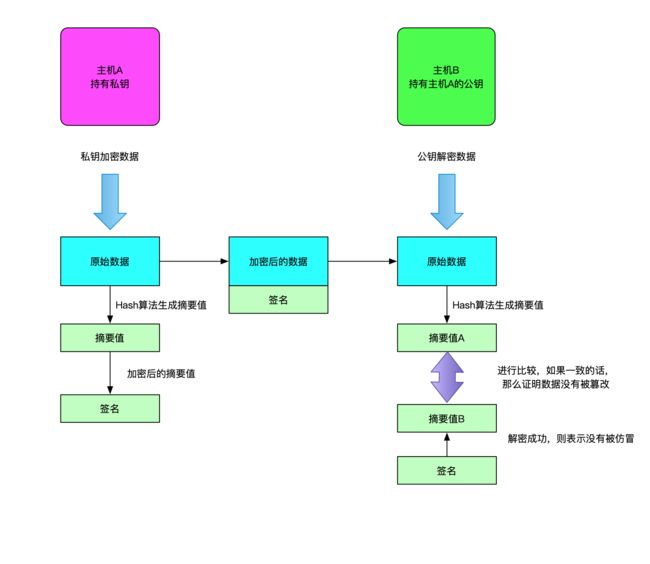
假如正在通信的主机A和主机B,主机A持有私钥,主机B持有主机A的公钥;
首先,主机A使用Hash算法对数据生成一段摘要值,然后再用私钥对这个摘要值加密,并将这个摘要值附在数据后面,发送给主机B;
主机B接收到数据后,使用公钥对这个摘要进行解密,然后再使用Hash算法对数据生成摘要值,将生成的摘要值,和解密后的摘要值进行比较,如果一致,那么则认为该数据持有的人是对的人,而不是被假冒的第三方;
第一种情况,使用公钥加密,私钥解密:
第二种情况,使用私钥加密,公钥解密:
看到这里,你是否会有疑惑,这两种情况是否还存在风险呢?
假如第一种情况,公钥被别人盗取了,那么别人就可以用这个公钥来假冒身份进行通信,而通信的对方识别不出来;
第二种情况,私钥泄露了,那么同理别人也可以用这个私钥来假冒身份进行通信;
那么怎么解决以上这两种问题呢?
那么就轮到我们的主角登场了,那就是:数字证书;
5.2、数字证书
数字证书是什么?
说的通俗易懂的,数字证书其实就相当于身份证,用于证明你是你,而不是被别人冒充的你,而数字证书的作用,用于在服务器出示证书验证身份用的;
作用就是为了避免第三方攻击,也就是别人冒充你去和对方进行通信,在通信的时候起到鉴别身份的作用;
数字证书是怎么起到鉴别身份的作用呢?
数字证书是由一个权威机构颁发的,这个权威机构叫CA,英文全称:certificate authority,又被称为证书中心;
这个CA中心,类似于公安局那种权威机构,给我们办理的身份证就是权威的,其他机构可信任的;
而CA中心就是这种原理,颁发的证书,可以被浏览器和客户端所信任;
接下来我们来看看证书都包含着哪些内容?
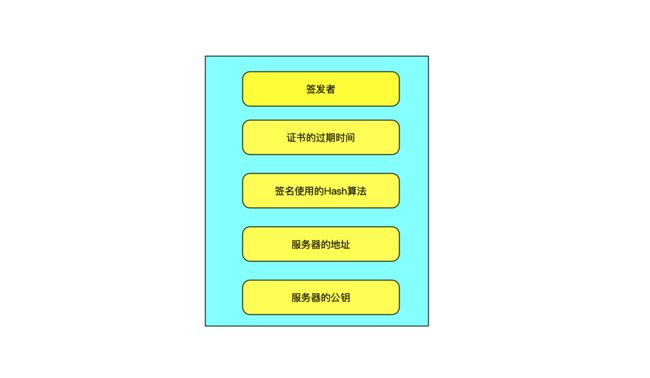
其实有一个很简单的方法,打开浏览器,输入百度的地址,然后点击左上角的锁头就能看到百度网站使用的证书,如图:
从上图可以看出,证书主要包含的主要内容有:
下面我们来看看数字证书是怎么验证身份的;
假设浏览器和服务器正在进行HTTPS通信:
首先,服务器会先把他的数字证书发送给浏览器,也就是上面图片这个,但是这个证书的相关内容是被CA的私钥加密过的;
浏览器持有CA内嵌的证书,包含有CA的公钥,而这个内嵌的证书叫做根证书,浏览器收到服务器发送过来的数字证书,那么就用CA的公钥对这个证书进行解密,解密成功,则表示该证书可信任,那么就认为服务器的身份正常;
然后浏览器将验证解密后的数字证书,会验证证书的有效期,还有服务器的地址是否正确(避免钓鱼网站),提取证书里服务器的公钥验证签名,如果都验证通过了,那么才会进行正常的通信,如果验证不过,那么就会建立连接失败,或者是提示用户,该网站不可信,请谨慎访问,给用户选择权;
那么到这里你是否会有疑问了?黑客照着这个证书仿照一个不行吗?这样不就可以骗过浏览器了?
黑客拿不到CA机构的私钥,所以没法伪造证书,因此这个问题不成立;
那么你是否又会有疑问了,黑客去权威机构申请一个证书不就行了吗?
答案是不行的,为啥呢? 因为证书的申请是有一个严谨的流程的;
假设浏览器和服务器通过非对称算法来加密数据,那么下面我们通过流程图来看看浏览器和服务器是怎么通过数字证书来校验身份的;
6、SSL/TSL
6.1、什么是SSL?
SSL简称安全套接字协议,SSL协议是HTTPS的保障,HTTPS等于HTTP+SSL;
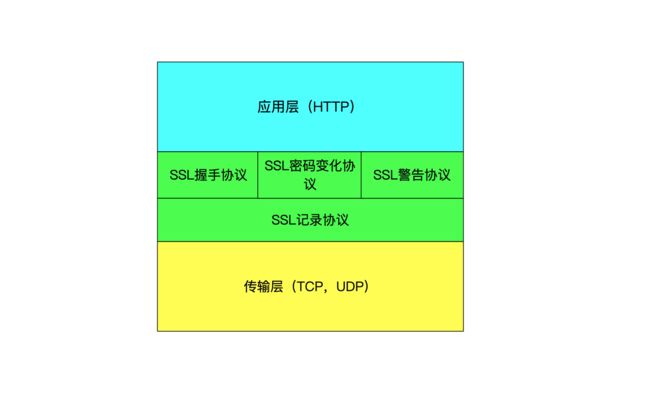
SSL协议位于应用层和传输层之间,用于保障通信双方的安全传输;
如图所示:
而TSL是SSL的升级版,虽然我们大多数时候称呼安全协议为SSL,但是大部分使用的都是TSL的协议;
我们上面讲的方案是使用非对称加密来进行安全传输的,而事实是非对称加密使用的算法比较耗时,那么我们真正商用的时候,不可能使用这种非对称算法来进行数据的加解密;
那么怎么解决这种缺陷呢?
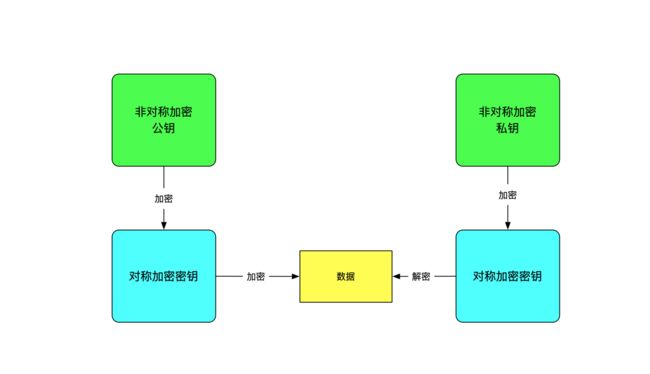
既然非对称加密算法比较耗时,而对称加密算法则不会很耗时,但是对称加密算法的密钥不安全,那么我们可以结合这两种加密算法来进行安全传输;
如图所示:
1,使用对称加密来加密数据;
2,使用非对称加密来加密对称加密的密钥;
那么SSL协议具体是怎么实现的呢?
SSL协议的具体实现并不像上面这种简单的实现,实际情况是,通过几次握手来进行密钥的协商,最终协商出通信双方使用的对称加密的密钥;
6.2、SSL协议
SSL协议的具体划分:
SSL体系分为SSL握手协议层和SSL记录协议层;
SSL握手协议层包含SSL握手协议,SSL密码变化协议,SSL警告协议,主要用于SSL的信息交换,协商加密算法以及密钥生成等操作;
SSL记录协议层主要针对应用层协议HTTP协议进行特别的设计,使HTTP协议能够在SSL协议层正常运行,主要用于加密解密,以及MAC校验等安全操作;
说了这么多,那么SSL协议是怎么来保证安全传输的呢?
别急,且听我细细道来;
6.3、SSL协议层是怎么建立连接的?
在上一篇文章,我讲了TCP连接是通过握手来建立连接的;
Android 网络编程之TCP、UDP详解
而SSL协议,促使通信的双方,通过SSL握手来建立通信的安全通道,那么SSL是怎么让HTTP达到安全传输的目的的呢?
在开始讲之前,我们来思考几个问题;
(1)SSL握手总共有几次?
(2)SSL握手是怎么协商密钥的?
(3)SSL安全通道是否可复用?
接下来,让我们带着这几个问题,来学习SSL握手吧;
我们先来看一下SSL握手的流程图:
假设我们通过客户端访问百度网站,客户端向服务器发起请求,此时双方还没有建立起安全通信;
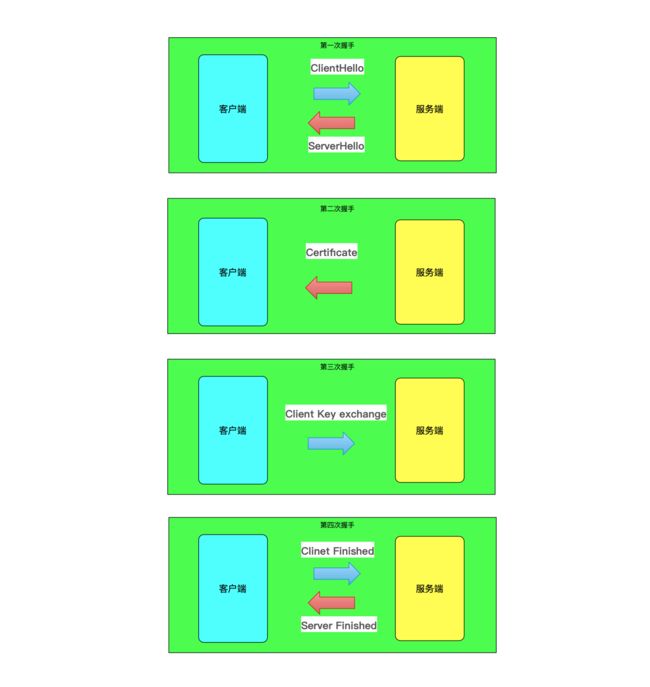
第一次握手:
客户端向服务器发送ClientHello消息,这个消息包含一个随机数 Random1(用于后续生成密钥使用),客户端支持哪种加密的相关信息(加密套件),SSL版本等信息;
服务器收到消息后,那么就会回客户端一个ServerHello消息,包含一个随机数Random2,以及服务器使用哪种加密的相关信息(加密套件),那么这时候客户端和服务器都有了两个随机数:Random1 + Random2;
从上面可以看出,第一次握手的主要作用的沟通协商通信双方支持的加密信息,以及生成随机数;
第二次握手:
第二次握手由服务器发起,服务器向客户端发送Certificate消息,消息包含数字证书,然后客户端验证服务器发送过来的证书,验证完毕后,取出证书中公钥,这里客户端是怎么通过数字证书验证身份的,上面已经讲过了,这里就不再多说;
从上面可以看出第二次握手主要作用是校验身份,这里主要是客户端校验了服务器的身份,如果服务器要求客户端也要校验身份,那么客户端也需要将数字证书发送给服务端;
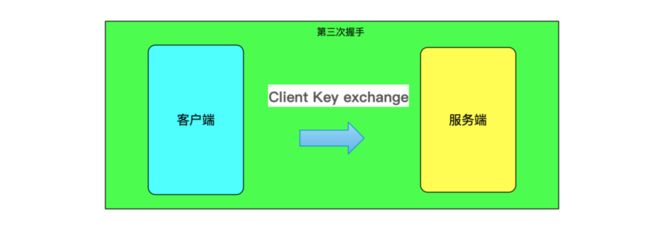
第三次握手:
第三次握手由客户端发起,客户端向服务器发送Client Key exchange消息,客户端生成一个随机数Random3,然后使用服务器的公钥加密这个随机数Random3,生成pre-master,然后将这个加密后的pre-master发送给服务器;
服务器接收到这个使用公钥加密后的pre-master,然后服务器使用私钥解密这个pre-master,得到Random3,那么这时候服务器和客户端都持有Random1 + Random2 + Random3;
那么这个东西是用来干嘛的呢?
答案是:对称机密
服务端和客户端使用这一串随机数,使用相同的算法生成对称加密的密钥,用于通信的双方的数据加密;
而这一串随机数的生成,避免了对称加密的密钥泄露的问题;
第四次握手:
第四次握手客户端向服务器发送一个加密后的消息,使用对称密钥加密消息,使用非对称密钥加密对称加密的密钥,然后使用非对称密钥进行签名,这个上面已经讲过了,这里就不再多说;
而服务器也使用同样的操作向客户端发送一个加密后的消息;
第四次握手的主要作用是用于检验通信的双方协商的密钥是否有效;
下面请看具体的流程图:
当然,实际的握手比这个还要复杂,因为涉及到太多计算机专业术语,这里不打算讲太多,容易把人绕晕,能理解过程就可以了;
如果有想要深入了解的小伙伴,可以看看这篇文章,讲的很详细:
SSL/TLS协议详解
6.4、SSL协议优化
那么看到这里,你是否会有疑问,如果客户端和服务端每次进行HTTPS通信的时候,都需要进行四次握手来建立安全通道,那么这样会造成很大的开销,而HTTPS作为商用的通信机制,那么肯定是已经考虑过这个问题了,那么到底是怎么解决的呢?
答案是:SSL会话复用;
会话复用,说白了就是已经建立过一次HTTPS连接的双方,当再次通信时,可以复用之前已经建立好的通道;
那么到底是怎么做到复用的呢?
有两种方案:
第一种方案:session ID机制;
1,首先,如果客户端和服务器已经成功建立连接,那么服务器就会返回一个session ID给客户端,服务器会保存这个session ID相关的通信信息;
2,当客户端再次发起HTTPS请求时,会将这个session ID传给服务器;
3,服务器接收到session ID后,通过session ID获取本地的缓存,判断缓存是否过期,如果没有过期,那么则继续复用该session ID对应的通信信息,于是直接跳过了前三次握手,直接进去第四次握手;
4,如果第四次握手双方验证数据成功后,那么就表示第四次握手成功,双方可以进行通信了;
看到这里你是否发现了一个问题,如果每个服务器将每个客户端的session ID相关信息都保存到服务器的话,那么就会面临占用资源过大的问题,如果客户端较少,那么该问题不存在,但是现实是客户端的数量是巨大的,服务器得考虑性能问题;
那么这个问题要怎么解决呢? 请看第二种方案;
第二种方案:session ticket;
1,如果客户端和服务端已经建立起连接了,那么服务器会将使用公钥加密后的session ticket发送给客户端,由客户端来保存;
2,如果客户端需要和服务端再次建立连接,那么就会将session ticket相关的加密信息发送给服务端;
3,如果服务器可以正常解密这个session ticket,那么表示该session ticket有效,那么服务器就会进入第四次握手,如果解密失败,那么按正常的握手流程走;
4,如果客户端解密服务器的数据成功后,那么第四次握手成功;
方案二与方案一不同的地方,在于将对应的通信信息,放到客户端来保存,由非对称密钥来保证安全性,大大的降低了服务器的压力;
很高兴再次见到你!
上面我们讲了一堆东西,Hash,对称加密,非对称加密,数字证书,SSL等相关知识,那么HTTPS具体是怎么实现的呢?
那么请看下面最后的总结
总结
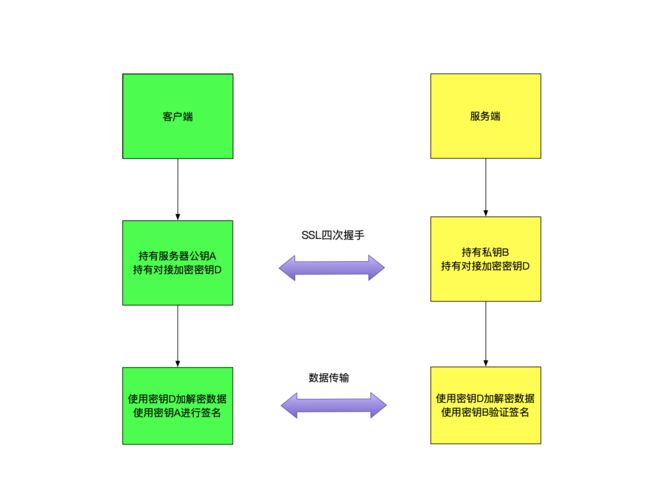
HTTPS的实现原理
HTTPS的实现,等于HTTP+SSL,而SSL协议做的主要工作是,帮助通信的双方,建立起通信的安全通道,通过四次握手,进行身份验证,密钥协商等操作,让服务器与客户端通过对称加密算法进行数据的加密,然后通过非对称加密算法来进行数据的签名,保证数据的完整性,以此来达到安全传输的目的;
请看最后总结的流程图:
从这里可以看出,最重要的一步,就是SSL协议,是HTTPS的基石;
那么到这里HTTPS相关的知识就已经讲完了,如果你有更好的观点,或者文中有哪些不合理的,都可以在评论区留言;
参考&感谢
算法科普:神秘的 DES 加密算法
RSA算法原理(一)
RSA算法原理(二)
通俗理解数字签名,数字证书和https
证书颁发机构
SSL/TLS协议详解
SSL/TLS 握手过程详解
HTTPS系列干货(一):HTTPS 原理详解
SSL/TLS 握手过程详解
其他
Android 你不得不学的HTTP相关知识
Android 网络编程之TCP、UDP详解
关于我
兄dei,如果我的文章对你有帮助的话,请帮我点个赞吧️,也可以关注一下我的Github和博客;