五、卷积神经网络CNN3（2D与3D卷积、池化）

2D卷积

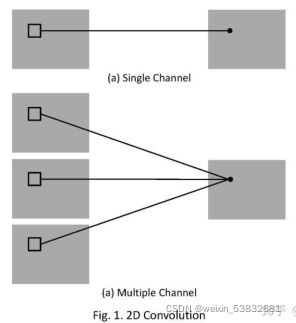
2D 卷积操作如图 1 所示，为了解释的更清楚，分别展示了单通道和多通道的操作。且为了画图方便，假定只有 1 个 filter，即输出图像只有一个 chanel。

其中，针对单通道，输入图像的 channel 为 1，卷积核尺寸为 (k_h, k_w, 1)，卷积核在输入图像上的的空间维度（即(height, width)两维）上进行进行滑窗操作，每次滑窗和 (k_h,k_w) 窗口内的 values 进行卷积操作（现在都用相关操作取代），得到输出图像中的一个value。

针对多通道，假定输入图像的 channel 为 3，卷积核尺寸为 (k_h, k_w, 3)， 卷积核在输入图像上的的空间维度（即(h, w)两维）上进行进行滑窗操作，每次滑窗与 3 个 channels上的 (k_h, k_w) 窗口内的所有的 values 进行相关操作，得到输出图像中的一个 value。

3D卷积

3D 卷积操作如图 2 所示，同样分为单通道和多通道，且只使用一个 filter，输出一个channel。

其中，针对单通道，与 2D 卷积不同之处在于，输入图像多了一个 length 维度，卷积核也多了一个 k_l 维度，因此卷积核在输入 3D 图像的空间维度（height 和 widthw 维）和 length维度上均进行滑窗操作，每次滑窗与 (k_h, k_w, k_l) 窗口内的 values 进行相关操作，得到输出 3D 图像中的一个value.

针对多通道，则与 2D 卷积的操作一样，每次滑窗与 3 个 channels 上的 (k_h, k_w, k_l)窗口内的所有 values 进行相关操作，得到输出 3D 图像中的一个 value。

池化方法

在卷积神经网络中，我们经常会碰到池化操作，而池化层往往在卷积层后面，通过池化来降低卷积层输出的特征向量，同时改善结果（不易出现过拟合）。
为什么可以通过降低维度呢？
因为图像具有一种“静态性”的属性，这也就意味着在一个图像区域有用的特征极有可能在另一个区域同样适用。因此，为了描述大的图像，一个很自然的想法就是对不同位置的特征进行聚合统计，例如，人们可以计算图像一个区域上的某个特定特征的平均值 (或最大值)来代表这个区域的特征。

一般池化（General Pooling ）

 池化作用于图像中不重合的区域（这与卷积操作不同），过程如下图。

我们定义池化窗口的大小为 sizeX，即下图中红色正方形的边长，定义两个相邻池化窗口的水平位移/竖直位移为 stride。一般池化由于每一池化窗口都是不重复的，所以 sizeX=stride。

最常见的池化操作为平均池化 mean pooling 和最大池化 max pooling：
平均池化：计算图像区域的平均值作为该区域池化后的值。
最大池化：选图像区域的最大值作为该区域池化后的值。

重叠池化（OverlappingPooling ）

重叠池化正如其名字所说的，相邻池化窗口之间会有重叠区域，此时 sizeX>stride。

空金字塔池化（Spatial Pyramid Pooling ）

空间金字塔池化可以把任何尺度的图像的卷积特征转化成相同维度，这不仅可以让 CNN处理任意尺度的图像，还能避免 cropping 和 warping 操作，导致一些信息的丢失，具有非常重要的意义。

一般的 CNN 都需要输入图像的大小是固定的，这是因为全连接层的输入需要固定输入维度，但在卷积操作是没有对图像尺度有限制，所有作者提出了空间金字塔池化，先让图像进行卷积操作，然后转化成维度相同的特征输入到全连接层，这个可以把 CNN 扩展到任意大小的图像。

空间金字塔池化的思想来自于 Spatial Pyramid Model，它一个 pooling 变成了多个 scale 的pooling。用不同大小池化窗口作用于卷积特征，我们可以得到 1X1,2X2,4X4 的池化结果，由于 conv5 中共有 256 个过滤器，所以得到 1 个 256 维的特征，4 个 256 个特征，以及 16 个 256维的特征，然后把这 21 个 256 维特征链接起来输入全连接层，通过这种方式把不同大小的图像转化成相同维度的特征。

 对于不同的图像要得到相同大小的 pooling 结果，就需要根据图像的大小动态的计算池化窗口的大小和步长。假设 conv5 输出的大小为 a*a，需要得到 n*n 大小的池化结果，可以让窗口大小 sizeX[a/n] 为 ，步长为[a/n] 。下图以 conv5 输出的大小为 13*13 为例。

疑问：如果 conv5 输出的大小为 14*14，[pool1*1]的 sizeX=stride=14，[pool2*2]的
sizeX=stride=7，这些都没有问题，但是，[pool4*4]的 sizeX=5，stride=4，最后一列和最后一行
特征没有被池化操作计算在内。
SPP 其实就是一种多个 scale 的 pooling，可以获取图像中的多尺度信息；在 CNN 中加入SPP 后，可以让 CNN 处理任意大小的输入，这让模型变得更加的 flexible。