关联规则挖掘之FPGrowth算法实现

1 关联规则挖掘之FPGrowth算法实现

Apriori算法通过利用频繁集的两个特性，过滤了很多无效集合，提高了算法效率。但是算法每一次对频繁项集的筛选都需要扫描一次原始数据集，对于大规模数据集Apriori的算法效率不尽如人意。

FPGrowth算法由韩家炜[1]等人于2004年提出，其中FPTree是使得这一算法相比Apriori等算法较为高效的关键数据结构，FPTree将数据库中的所有事务(Transactions)高度压缩成树的路径，所有的频繁项(Frequent Items, FIs)都成为树的一个节点，每个节点都拥有相应的计数，代表该FIs在数据库中出现的次数，其中叶子节点的计数等于前向遍历路径中的FIs出现在数据库中的次数。因此所有的挖掘工作都以最初的FPTree为中心展开，而在构建一棵FPTree时，核心步骤在于对每一条事务进行降序排序。

1.1 FPTree的构建

• 树结构设计

def __init__(self,idName,count=1):
    """构造函数
    Args:               Type        Meaning
        idName          String      编号
        count           int         计数
        next            FpNode      下一个id号相同的结点
        parent          FpNode      父结点
        children        List[FpNode]孩子结点
    """
    self.idName = idName    #根结点为None
    self.count = count      #根结点为-1
    self.next = None             
    self.parent = None      
    self.children = []

• 算例演示

  同样我们以在关联规则挖掘之Apriori算法实现中的购物篮数据集为例演示FPTree的构造，频繁项的绝对支持度设置为3。

  TID	Items
  T1	{牛奶，面包，1}
  T2	{面包，尿布，啤酒，鸡蛋，1}
  T3	{牛奶，尿布，啤酒，可乐，1}
  T4	{面包，牛奶，尿布，啤酒，1}
  T5	{面包，牛奶，尿布，可乐，1}

表中每一条记录中的数字表示记录出现的次数，如T1，{牛奶，面包，1}中的1表示同时购买牛奶，面包的记录出现了1次。

• Step1：第一次扫描原始数据集，得到所有满足最小支持度阈值的频繁1项集，并按照项的计数降序排列；

  Item	Count(desending)
  牛奶	4
  面包	4
  尿布	4
  啤酒	3

• Step2：第二次扫描原始数据集，删除每条数据中的非频繁1项集，并按照计数降序排列每条数据中的项；

  注意：这里降序排列时，一定要保证项的相对顺序，如这里选择了频繁1项集的排序为牛奶、面包、尿布、啤酒，那么数据集中的每一条数据（这里已经去除了非频繁1项集）都应该按照频繁1项集中项的相对顺序排列。

  构建FPTree，初始时，新建一个标记为None的空节点。按顺序扫描记录，将记录中项添加到FPTree中。

  • 第1条记录：{牛奶，面包，1}降序排列够得到{牛奶，面包，1}，新建一个结点，idName为**“牛奶”，将其插入到根节点下，并设置count为记录中的数字即1，然后新建一个“面包”结点，插入到“牛奶”**结点下面。插入后如下所示：

同时，为了便于候选在FPTree上挖掘频繁项集，我们构建了一个线索表，线索表中元素由频繁1项集按照计数降序排列组成。随着FPTree的构建，将同idName的结点地址相连。如示例中的线索表为{牛奶：[牛奶结点地址]，面包：[面包结点地址]，尿布：[尿布结点地址]，啤酒：[啤酒结点地址]}。

• 第2条记录：{面包，尿布，啤酒，鸡蛋，1}，删除非频繁1项集再降序后得到：{面包，尿布，啤酒，1}。访问FPTree的根结点None，发现其子结点没有包含面包，因此新建一个面包结点，将其作为根节点None的第2个子结点，随后新建尿布结点上接新建面包结点，下接新建啤酒结点，并根据新建结点更新线索表，新建结点的计数均为所在记录的计数。

• 第3条记录：{牛奶，尿布，啤酒，可乐，1}，删除非频繁1项集再降序后得到：{牛奶，尿布，啤酒，1}。访问FPTree的根结点None，发现其子结点上含有牛奶结点，则将牛奶结点的计数+新记录中的计数（这里为1）；接着访问牛奶结点的子结点，发现牛奶结点的子结点中无尿布结点，因此新建尿布结点，上接已有牛奶结点，下接新建啤酒结点，并根据新建结点更新线索表，新建结点的计数均为所在记录的计数。
  
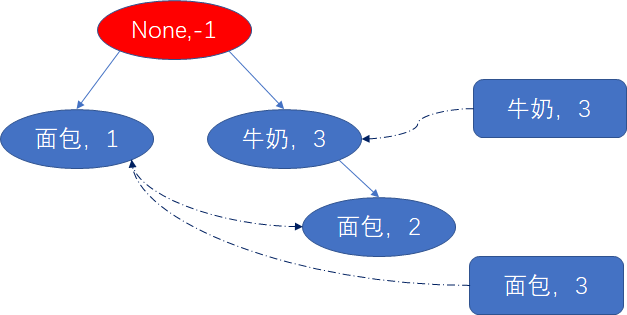
• 第4条记录：{面包，牛奶，尿布，啤酒，1}，删除非频繁1项集再降序后得到{牛奶，面包，尿布，啤酒}。访问FPTree的根结点None，发现其子结点上含有牛奶结点，则牛奶结点计数+当前记录的计数；继续访问牛奶结点的子结点，子结点中含有面包结点，同样将面包结点计数+当前记录的计数；继续访问面包结点的子结点，发现子结点中并无尿布结点，因此新建尿布结点上接面包结点，下接新建啤酒结点，并根据新建结点更新线索表；同样，新建结点的计数均为所在记录的计数。

• 第5条记录：{面包，牛奶，尿布，可乐，1}，删除非频繁1项集再降序后得到：{牛奶，面包，尿布，1}。访问FPTree的根结点，发现其子结点上包含牛奶结点，将牛奶结点计数+当前记录的计数；继续访问牛奶结点的子结点，包含面包结点，则将面包结点计数+当前记录的计数；继续访问面包结点的子结点，包含尿布结点，将尿布结点的计数+当前记录的计数。

  

1.2 利用FPTree挖掘频繁项集

频繁项集的挖掘从线索表表头的最后一项开始，依次从后往前挖掘，如此例中，线索表的表头为[牛奶，面包，尿布，啤酒]，那么挖掘顺序为啤酒$\to$尿布$\to$面包$\to$牛奶。挖掘流程如下：

1. 此例中从啤酒开始，根据啤酒的线索链找到所有包含啤酒的结点，然后找出每个包含啤酒结点的分支：

   {牛奶，面包，尿布，啤酒，1}，{牛奶，尿布，啤酒，1}，{面包，尿布，啤酒，1}，其中的1表示分支出现的次数为1次，由分支中啤酒的计数决定。除去分支中的啤酒，得到新的数据记录{牛奶，面包，尿布，1}，{牛奶，尿布，1}，{面包，尿布，1}。然后按照FPTree的构建方式构建啤酒的条件FPTree。

   • 啤酒分支对应的数据集

   TID	Items
   T1	{牛奶，面包，尿布，1}
   T2	{牛奶，尿布，1}
   T3	{面包，尿布，1}

   • 啤酒的条件FPTree

构造好条件树后，对条件树进行递归挖掘，递归的终止条件为当前条件树只有一条路径，此时路径的所有组合即为条件频繁集。如当前啤酒的条件频繁集为{{}，尿布}，于是啤酒的频繁集为{{啤酒}，{尿布，啤酒}}

2. 接下来找线索表表头的倒数第2项尿布的频繁集，同理可以得到尿布的前缀路径为：{面包，1}，{牛奶，1}，{牛奶，面包，2}

   • 尿布分支对应的数据集

   TID	Items
   T1	{面包，1}
   T2	{牛奶，1}
   T3	{牛奶，面包，2}

   • 尿布对应的条件FPTree

由于当前条件树中存在两条路径，因此进行递归挖掘。从尿布线索表表头的最后一项即面包项开始进行挖掘。同理面包的前缀路径为，{牛奶，2}

• 面包分支对应的数据集

  TID	Items
  T2	{牛奶，2}

由于当前数据集不满足最小绝对支持度的要求，因此面包的条件FP树为None，满足条件FPTree的路径数仅有一条的条件，因此当前面包的条件频繁项集为{}，面包的频繁集为{面包}。

同理尿布线索表表头的剩余项牛奶的频繁集为{牛奶}

最终：尿布的频繁集为{{尿布}，{牛奶，尿布}，{面包，尿布}}（**注意：**尿布自身也是频繁集）

重复以上步骤，对线索表中的每个项进行挖掘，即可得到整个频繁项集。

1.3 参考

[1] Han jia wei, Pei Jan等 Mining Frequent Patterns without Candidate Generation: A Frequent-Pattern Tree Approach.2004.

[2] https://www.cnblogs.com/fengfenggirl/p/associate_fpgowth.html.

1.4 代码实现

• 树结点的设计

  
  class FpNode:
      def __init__(self,idName,count=1):
          """构造函数
          Args:               Type        Meaning
              idName          String      编号
              count           int         计数
              next            FpNode      下一个id号相同的结点
              parent          FpNode      父结点
              children        List[FpNode]孩子结点
          """
          self.idName = idName    #根结点为None
          self.count = count      #根结点为-1
          self.next = None             
          self.parent = None      
          self.children = []    
      
    
      def addChild(self,child):
          """添加一个孩子结点
          Args:               Type
              child           FpNode
          """
          self.children.append(child)
      
      def addCount(self,count=1):
          self.count += count
      
      def setNextNode(self,next):
          """设置下一个结点
          Args:           Type
              next        FpNode
          """
          self.next = next
      
      def setParent(self,parent):
          """设置父结点
          Args:           Type
              parent      FpNode
          """
          self.parent = parent
      
      def getChild(self,index):
          """指定索引取孩子
          Args:           Type
              index       int
          """
          return self.children[index]
  
      def hasChild(self,idName):
          """查找是否包含id为idName的孩子
          Args:           Type
              idName      string
          """
          for i in range(len(self.children)):
              if self.children[i].idName == idName:
                  return i
          return -1
      
      def __repe__(self):
  
          return "id: " + self.idName + "count: " + str(self.count) \
              + "孩子个数" + str(len(self.children))
  

• FPTree的构建

  
  from FpNode import FpNode
  
  class FpTree:
      def __init__(self,dataSets,min_num):
          self.dataSets = dataSets        #待挖掘数据集，[[...,count],[...,count],...]
          # self.min_num = round(min_support * FpTree.countnum(dataSets))   #最小支持数=最小支持度*数据量
          self.min_num = min_num
      
    
      
      def scan1(self):
          """构建项头表，也就是按照频次降序的频繁1项集
          Returns:
              L1          频繁1项集{1项集:计数}
          """
         
          L1 = {}         #频繁1项集
          for record in self.dataSets:
              for item in record[:-1]:
                  if item in L1.keys():
                      L1[item] += record[-1]
                  else:
                      L1[item] = record[-1]
          delrecord = []      #记录不满足支持度的项，非频繁项
          for item,count in L1.items():
              if count < self.min_num:
                  delrecord.append(item)
          if delrecord:
              for item in delrecord:
                  del L1[item]
  
          L1List = sorted(L1.items(),key=lambda x:x[1],reverse=True) 
          L1.clear()  
          for item in L1List:
              L1[item[0]] = item[1]
          return L1
          
      def scan2(self,L1):
          """删除样本数据集中的非频繁1项集，并按照频繁1项集的计数排序
          Args:
              L1              频繁1项集{1项集:计数}
          Returns
              record          删除非频繁1项集后的数据
          """
          record = []
          for row in self.dataSets:
              newrow = []
              for key in L1.keys():       #频繁1项集
                  if key in row[:-1]:
                      newrow.append(key)
              if newrow:
                  newrow.append(row[-1])  #加上计数
                  record.append(newrow)
                  
          return record
  
      def createFpTree(self,L1,Ls):
          """构建Fp树
          Args:
              L1              频繁1项集
              Ls              去除非频繁1项集后的记录
          Returns:
              headerTable     线索表
              root            Fp树根
          """
          nodeLinkTable = {idName:FpNode(idName,num) for idName,num in L1.items()} #线索表
          headerTable = nodeLinkTable.copy()
          root = FpNode(None,-1)
          for L in Ls:
              currentRoot = root                                  #根结点
              for idName in L[:-1]:
                  index = currentRoot.hasChild(idName)            #当前结点是否在当前根结点的子结点中
                  if index >= 0:
                      currentNode = currentRoot.getChild(index)   #是，则取出
                      currentNode.addCount(L[-1])                 #结点出现次数加上当前记录的重复次数
                  else:                                           #否，则新建结点
                      currentNode = FpNode(idName,L[-1])
                      currentNode.parent = currentRoot
                      currentRoot.addChild(currentNode)
                      nodeLinkTable[idName].setNextNode(currentNode)  #记录同idName的项
                      nodeLinkTable[idName] = currentNode
  
                  currentRoot = currentNode
              
          return headerTable,root
  
      @staticmethod
      def levelOrderTraversal(root):
          """层序遍历，检测Fp树是否构建完整"""
          record = [] #记录每一层的idName
          Q = [root]
          while Q:
              currentNode = Q.pop(0)
              record.append(currentNode.idName)
              Q.extend(currentNode.children)
          return record
  

• 频繁项集的挖掘

  
  from FpTree import FpTree
  def conditionFpTree(leafNode):
      """生成指定项的条件树
      Args:
          headerTable         线索表头
          root                Fp树根
          leafNode            指定项
      """
      ###首先找到所有包含指定项的分支，并以指定项截断###
      newLs = []              #包含指定项的所有分支记录，以指定项截断
      while leafNode:
          currentNode = leafNode
          L = []
          Flag = True    #标注是否与当前结点相连的仅有根结点
          while currentNode.parent and currentNode.parent.idName != None:
              L.append(currentNode.parent.idName)
              currentNode = currentNode.parent
              Flag = False
          if not Flag:
              L.append(leafNode.count)
              newLs.append(L)
          leafNode = leafNode.next
      ###其次计算新的频繁1项集和去除非频繁项后的所有分支记录###
      ft = FpTree(newLs,3)            #创建新树实例
      newL1 = ft.scan1()  #新的频繁1项集
      newLs = ft.scan2(newL1)      #去除非频繁项后的分支记录
      ###最后构建指定项的条件树###
      newheaderTable,newroot = ft.createFpTree(newL1,newLs)
      return newheaderTable,newroot
   
   #层次遍历树，当只有一个叶结点时，表明条件树只有一条路径
  def isSingleLeaf(root):
      """层序遍历
      Args:
          root        根结点
      Returns:
          bool        树是否有分支
      """
      record = [] #记录每一层的idName
      Q = [root]
      while Q:
          currentNode = Q.pop(0)
          record.append(currentNode.idName)
          Q.extend(currentNode.children)
      return len(record) <= 2     #[None]或者[None,item]
  
  def frequent(condTreeItems):
      """生成仅有一条路径的condTree上的所有频繁项集
      Args:
          condTreeItems    条件模式基[item1,item2,....]
      Returns:
          fks         频繁项集
      """
      fks = [[]]
      for item in condTreeItems:
          fks += [items + [item] for items in fks]
  
      return fks
  
  def miningFrequentSet(leafNode):
      """递归挖掘指定项的频繁集
      Args:           Type
          leafNode    FpNode
      Returns:
  
      """
      frequentSet = []
      currentHeaderTable,currentRoot = conditionFpTree(leafNode)
      if currentHeaderTable == dict():
          frequentSet.append([leafNode.idName])
          return frequentSet
      if isSingleLeaf(currentRoot):       #判断条件树是否是单树
          if currentRoot.children:
              condTreeItems = []
              currentNode = currentRoot.children[0]
              while currentNode:
                  condTreeItems.append(currentNode.idName)
                  if currentNode.children:
                      currentNode = currentNode.children[0]
                  else:
                      break
              frequentSet = frequent(condTreeItems)
          if frequentSet:
              for s in frequentSet:
                  s.append(leafNode.idName)
          else:
              frequentSet.append([leafNode.idName])
          return frequentSet
      else:
          targetIdName = leafNode.idName
          leafNodeIdNames = list(currentHeaderTable.keys())
          leafNodeIdNames.reverse()
          for leafNodeIdName in leafNodeIdNames:
              leafNode = currentHeaderTable[leafNodeIdName]
              currentFrequenSet = miningFrequentSet(leafNode)
              currentFrequenSet = [subset + [targetIdName] for subset in currentFrequenSet]   #以指定频繁项结尾
              frequentSet.extend(currentFrequenSet)
          frequentSet.append([targetIdName])  #加上自己
      return frequentSet
  
  def loadDatas(testdata=1):
      if testdata==1:
          dataSets = [['牛奶','面包',1],
          ['面包','尿布','啤酒',1],
          ['牛奶','尿布','啤酒',1],
          ['牛奶','面包','尿布','啤酒',1],
          ['牛奶','面包','尿布',1]
          ]
      else:
          dataSets = [['A','C','E','B','F',1],\
              ['A','C','G',1],\
              ['E',1],\
              ['A','C','E','G','D',1],\
              ['A','C','E','G',1],\
              ['E',1],\
              ['A','C','E','B','F',1],\
              ['A','C','D',1],\
              ['A','C','E','G',1],\
              ['A','C','E','G',1]]
  
      return dataSets
  # L1 = {'牛奶':4,'面包':4,'尿布':4,'啤酒':3}
  def main():
      dataSets = loadDatas(1)
      ft = FpTree(dataSets,3)
      L1 = ft.scan1()
      Ls = ft.scan2(L1)
      # print(L1)
      # print(Ls)
      headerTable,root = ft.createFpTree(L1,Ls)           #创建Fp树
      currentHeaderTable,currentRoot = headerTable,root
      nodeIdNames = list(currentHeaderTable.keys())
      nodeIdNames.reverse()#倒序，即按照项出现次数升序排列，先挖掘出现次数少的
      
      # print(nodeIdNames)
      for idName in nodeIdNames:
          leafNode = currentHeaderTable[idName].next
          print(miningFrequentSet(leafNode),end='\n')
  if __name__ == "__main__":
      main()