【智能车】模糊PID控制原理详解与代码实现
模糊PID控制
本文主要由三部分构成:模糊PID控制器的原理,模糊PID控制器C++的实现与测试。
一. 模糊PID原理
模糊PID控制流程如下图所示,把目标值 Xtarget 与输出值 Xout 的误差 e 与 e 的变化率 de/dt 作为模糊控制器的输入,模糊控制器先对输入进行模糊化处理,接着进行模糊推理,最后把模糊推理的结果进行去模糊处理输出PID控制器的三个参数 kp, ki, kd,从而达到对PID控制器参数自适应整定的效果。

根据以上的描述可知,模糊控制器主要由去模糊化,模糊推理以及去模糊三部分组成。以下将对三部分进行详细讲解。
1.1 模糊化
要实现模糊化首先需要对模糊化进行初始化,初始化包括论域的确定以及隶属度函数的确定。
1.1.1 论域
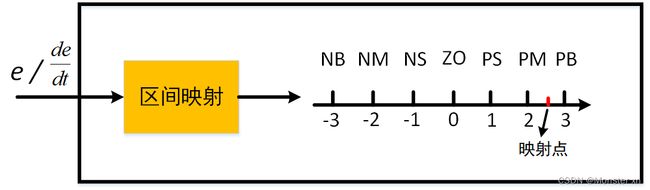
论域可以说是一个人为确定的范围,由于输入 e, de/dt,输出 kp, ki, kd 的范围各不相同,把输入映射到论域上更好统一处理。确定论域的范围后,需要对论域进行模糊分类,模糊分类即对论域进行划分。假设论域的范围为 [-3,3],把论域平均分为 5 等份,即 [-3, -2], [-2, -1], [-1, 0], [0, 1], [1, 2], [2, 3]。接着把每个端点进行等级划分,依次为: -3—>NB(负大), -2—>NM(负中), -1---->NS(负小), 0—>ZO(零), 1---->PS(正小), 2---->PM(正中), 3---->PB(正大)。假设输入e的范围为 [-10, 10],此刻 e 的值为 8,通过映射后的值为 2.4,2.4 在 [2, 3] 区间,则该点在正中与正大之间。示意图如下:
1.1.2 隶属度函数的确定。
常见的隶属度函数有三角形隶属度函数,梯形隶属度函数,抛物线型隶属度函数。以最简单的三角性隶属度函数为例,形状如下图所示:
由上图可知,隶属度函数的值域为 [0, 1]。若输入e经过映射后的值为 2.4,那么对应下图红线与绿线的值分别为 0.6,0.4, 这两个就是隶属度,表示该输入属于 PM 的概率为0.6,而属于 PB 的概率为0.4。所以隶属度也为概率。
由上述论域和隶属度函数的讲解,可总结出模糊化的过程:区间映射,根据隶属度函数计算隶属度,流程图如下:
1.2 模糊推理
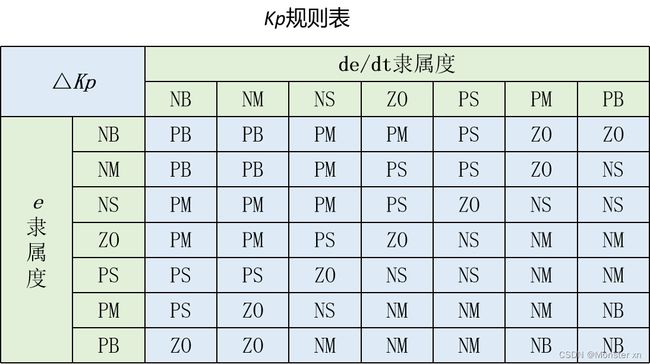
模糊推理,即根据 e 与 de/dt 的隶属度进行查表得到输出的大小程度,即 NB,NS 等。所以模糊推理的核心工作是建立推理表。其中模糊PID常用的推理表如下图所示:
以下以一个例子说明规则表的使用方法。
假设此刻的输入 e 为8,de/dt 为-12,而e的范围为[-10,10],de/dt 的范围为[-20,20]。则通过模糊化得到 e 的隶属度为0.6(PM)与0.4(PB),de/dt 的隶属度为0.8(NM)与0.2(NS),然后,对 e 与 de/dt 的隶属度进行两两组合,并进行查表,得到下表的关系:
接着,计算各输出 Kp, Ki, Kd 的隶属度。
以Kp为例:
同理 Ki, Kd 也计算隶属度。
最后进行个输出的隶属度进行整合,例如 Kp, 由上面计算可知,Kp 的隶属度为 0.8(ZO),0.12(NS),0.08(NM)。
1.3 去模糊
去模糊是根据模糊推理得到的各输出的隶属度算出输出在论域中的哪个值,然后根据区间映射关系,得到输出。
1.3.1 计算输出在论域中的值
以上面的例子进行阐述计算的过程。由上面可知,Kp 的隶属度为0.8(ZO),0.12(NS),0.08(NM), 而在论域讲解时,已经将 ZO 的值定为0,NS 的值定为-1,NM 的值定为-2。那么 Kp 的期望为:
把期望作为 Kp 在论域的值,在确定 Kp 的范围后,根据区间映射公式,可得出 Kp 的输出值。
以上为模糊控制器的流程。
值得注意的是,输出的 Kp, Ki, Kd 为增量。在初始化时要确定输入与输出的范围(区间),用于进行区间映射。
2.1 C++实现模糊PID控制器
该本版隶属度函数为固定三角形隶属度函数,论域固定为[-3, 3]。
FuzzyPID.h
#ifndef FuzzyPID_H
#define FuzzyPID_H
class FuzzyPID
{
public:
FuzzyPID();
~FuzzyPID();
void Get_grad_membership(float erro, float erro_c);
float Quantization(float maximum, float minimum, float x);
float Inverse_quantization(float maximum, float minimum, float qvalues);
void GetSumGrad();
void GetOUT();
float FuzzyPIDcontroller(float e_max, float e_min, float ec_max, float ec_min, float kp_max, float kp_min, float erro, float erro_c, float ki_max, float ki_min,float kd_max, float kd_min,float erro_pre, float errp_ppre);
const int num_area = 8; //划分区域个数
//float e_max; //误差做大值
//float e_min; //误差最小值
//float ec_max; //误差变化最大值
//float ec_min; //误差变化最小值
//float kp_max, kp_min;
float e_membership_values[7] = {-3,-2,-1,0,1,2,3}; //输入e的隶属值
float ec_membership_values[7] = { -3,-2,-1,0,1,2,3 };//输入de/dt的隶属值
float kp_menbership_values[7] = { -3,-2,-1,0,1,2,3 };//输出增量kp的隶属值
float ki_menbership_values[7] = { -3,-2,-1,0,1,2,3 }; //输出增量ki的隶属值
float kd_menbership_values[7] = { -3,-2,-1,0,1,2,3 }; //输出增量kd的隶属值
float fuzzyoutput_menbership_values[7] = { -3,-2,-1,0,1,2,3 };
//int menbership_values[7] = {-3,-};
float kp; //PID参数kp
float ki; //PID参数ki
float kd; //PID参数kd
float qdetail_kp; //增量kp对应论域中的值
float qdetail_ki; //增量ki对应论域中的值
float qdetail_kd; //增量kd对应论域中的值
float qfuzzy_output;
float detail_kp; //输出增量kp
float detail_ki; //输出增量ki
float detail_kd; //输出增量kd
float fuzzy_output;
float qerro; //输入e对应论域中的值
float qerro_c; //输入de/dt对应论域中的值
float errosum;
float e_gradmembership[2]; //输入e的隶属度
float ec_gradmembership[2]; //输入de/dt的隶属度
int e_grad_index[2]; //输入e隶属度在规则表的索引
int ec_grad_index[2]; //输入de/dt隶属度在规则表的索引
float gradSums[7] = {0,0,0,0,0,0,0};
float KpgradSums[7] = { 0,0,0,0,0,0,0 }; //输出增量kp总的隶属度
float KigradSums[7] = { 0,0,0,0,0,0,0 }; //输出增量ki总的隶属度
float KdgradSums[7] = { 0,0,0,0,0,0,0 }; //输出增量kd总的隶属度
int NB = -3, NM = -2, NS = -1, ZO = 0, PS = 1, PM = 2, PB = 3; //论域隶属值
int Kp_rule_list[7][7] = { {PB,PB,PM,PM,PS,ZO,ZO}, //kp规则表
{PB,PB,PM,PS,PS,ZO,NS},
{PM,PM,PM,PS,ZO,NS,NS},
{PM,PM,PS,ZO,NS,NM,NM},
{PS,PS,ZO,NS,NS,NM,NM},
{PS,ZO,NS,NM,NM,NM,NB},
{ZO,ZO,NM,NM,NM,NB,NB} };
int Ki_rule_list[7][7] = { {NB,NB,NM,NM,NS,ZO,ZO}, //ki规则表
{NB,NB,NM,NS,NS,ZO,ZO},
{NB,NM,NS,NS,ZO,PS,PS},
{NM,NM,NS,ZO,PS,PM,PM},
{NM,NS,ZO,PS,PS,PM,PB},
{ZO,ZO,PS,PS,PM,PB,PB},
{ZO,ZO,PS,PM,PM,PB,PB} };
int Kd_rule_list[7][7] = { {PS,NS,NB,NB,NB,NM,PS}, //kd规则表
{PS,NS,NB,NM,NM,NS,ZO},
{ZO,NS,NM,NM,NS,NS,ZO},
{ZO,NS,NS,NS,NS,NS,ZO},
{ZO,ZO,ZO,ZO,ZO,ZO,ZO},
{PB,NS,PS,PS,PS,PS,PB},
{PB,PM,PM,PM,PS,PS,PB} };
int Fuzzy_rule_list[7][7] = { {PB,PB,PB,PB,PM,ZO,ZO},
{PB,PB,PB,PM,PM,ZO,ZO},
{PB,PM,PM,PS,ZO,NS,NM},
{PM,PM,PS,ZO,NS,NM,NM},
{PS,PS,ZO,NM,NM,NM,NB},
{ZO,ZO,ZO,NM,NB,NB,NB},
{ZO,NS,NB,NB,NB,NB,NB}};
//private:
};
#endif
FuzzyPID.cpp
#include "FuzzyPID.h"
FuzzyPID::FuzzyPID() //构造函数
{
kp = 0;
ki = 0;
kd = 0;
fuzzy_output = 0;
qdetail_kp = 0;
qdetail_ki = 0;
qdetail_kd = 0;
qfuzzy_output = 0;
errosum = 0;
}
FuzzyPID::~FuzzyPID()//析构函数
{
}
//输入e与de/dt隶属度计算函数///
void FuzzyPID::Get_grad_membership(float erro,float erro_c)
{
if (erro > e_membership_values[0] && erro < e_membership_values[6])
{
for (int i = 0; i < num_area - 2; i++)
{
if (erro >= e_membership_values[i] && erro <= e_membership_values[i + 1])
{
e_gradmembership[0] = -(erro - e_membership_values[i + 1]) / (e_membership_values[i + 1] - e_membership_values[i]);
e_gradmembership[1] = 1+(erro - e_membership_values[i + 1]) / (e_membership_values[i + 1] - e_membership_values[i]);
e_grad_index[0] = i;
e_grad_index[1] = i + 1;
break;
}
}
}
else
{
if (erro <= e_membership_values[0])
{
e_gradmembership[0] = 1;
e_gradmembership[1] = 0;
e_grad_index[0] = 0;
e_grad_index[1] = -1;
}
else if (erro >= e_membership_values[6])
{
e_gradmembership[0] = 1;
e_gradmembership[1] = 0;
e_grad_index[0] = 6;
e_grad_index[1] = -1;
}
}
if (erro_c > ec_membership_values[0] && erro_c < ec_membership_values[6])
{
for (int i = 0; i < num_area - 2; i++)
{
if (erro_c >= ec_membership_values[i] && erro_c <= ec_membership_values[i + 1])
{
ec_gradmembership[0] = -(erro_c - ec_membership_values[i + 1]) / (ec_membership_values[i + 1] - ec_membership_values[i]);
ec_gradmembership[1] = 1 + (erro_c - ec_membership_values[i + 1]) / (ec_membership_values[i + 1] - ec_membership_values[i]);
ec_grad_index[0] = i;
ec_grad_index[1] = i + 1;
break;
}
}
}
else
{
if (erro_c <= ec_membership_values[0])
{
ec_gradmembership[0] = 1;
ec_gradmembership[1] = 0;
ec_grad_index[0] = 0;
ec_grad_index[1] = -1;
}
else if (erro_c >= ec_membership_values[6])
{
ec_gradmembership[0] = 1;
ec_gradmembership[1] = 0;
ec_grad_index[0] = 6;
ec_grad_index[1] = -1;
}
}
}
/获取输出增量kp,ki,kd的总隶属度/
void FuzzyPID::GetSumGrad()
{
for (int i = 0; i <= num_area - 1; i++)
{
KpgradSums[i] = 0;
KigradSums[i] = 0;
KdgradSums[i] = 0;
}
for (int i=0;i<2;i++)
{
if (e_grad_index[i] == -1)
{
continue;
}
for (int j = 0; j < 2; j++)
{
if (ec_grad_index[j] != -1)
{
int indexKp = Kp_rule_list[e_grad_index[i]][ec_grad_index[j]] + 3;
int indexKi = Ki_rule_list[e_grad_index[i]][ec_grad_index[j]] + 3;
int indexKd = Kd_rule_list[e_grad_index[i]][ec_grad_index[j]] + 3;
//gradSums[index] = gradSums[index] + (e_gradmembership[i] * ec_gradmembership[j])* Kp_rule_list[e_grad_index[i]][ec_grad_index[j]];
KpgradSums[indexKp]= KpgradSums[indexKp] + (e_gradmembership[i] * ec_gradmembership[j]);
KigradSums[indexKi] = KigradSums[indexKi] + (e_gradmembership[i] * ec_gradmembership[j]);
KdgradSums[indexKd] = KdgradSums[indexKd] + (e_gradmembership[i] * ec_gradmembership[j]);
}
else
{
continue;
}
}
}
}
计算输出增量kp,kd,ki对应论域值//
void FuzzyPID::GetOUT()
{
for (int i = 0; i < num_area - 1; i++)
{
qdetail_kp += kp_menbership_values[i] * KpgradSums[i];
qdetail_ki += ki_menbership_values[i] * KigradSums[i];
qdetail_kd+= kd_menbership_values[i] * KdgradSums[i];
}
}
//模糊PID控制实现函数/
float FuzzyPID::FuzzyPIDcontroller(float e_max, float e_min, float ec_max, float ec_min, float kp_max, float kp_min, float erro, float erro_c,float ki_max,float ki_min,float kd_max,float kd_min,float erro_pre,float errp_ppre)
{
errosum += erro;
//Arear_dipart(e_max, e_min, ec_max, ec_min, kp_max, kp_min,ki_max,ki_min,kd_max,kd_min);
qerro = Quantization(e_max, e_min, erro);
qerro_c = Quantization(ec_max, ec_min, erro_c);
Get_grad_membership(qerro, qerro_c);
GetSumGrad();
GetOUT();
detail_kp = Inverse_quantization(kp_max, kp_min, qdetail_kp);
detail_ki = Inverse_quantization(ki_max, ki_min, qdetail_ki);
detail_kd = Inverse_quantization(kd_max, kd_min, qdetail_kd);
qdetail_kd = 0;
qdetail_ki = 0;
qdetail_kp = 0;
/*if (qdetail_kp >= kp_max)
qdetail_kp = kp_max;
else if (qdetail_kp <= kp_min)
qdetail_kp = kp_min;
if (qdetail_ki >= ki_max)
qdetail_ki = ki_max;
else if (qdetail_ki <= ki_min)
qdetail_ki = ki_min;
if (qdetail_kd >= kd_max)
qdetail_kd = kd_max;
else if (qdetail_kd <= kd_min)
qdetail_kd = kd_min;*/
kp = kp + detail_kp;
ki = ki + detail_ki;
kd = kd + detail_kd;
if (kp < 0)
kp = 0;
if (ki < 0)
ki = 0;
if (kd < 0)
kd = 0;
detail_kp = 0;
detail_ki=0;
detail_kd=0;
float output = kp*(erro - erro_pre) + ki * erro + kd * (erro - 2 * erro_pre + errp_ppre);
return output;
}
///区间映射函数///
float FuzzyPID::Quantization(float maximum,float minimum,float x)
{
float qvalues= 6.0 *(x-minimum)/(maximum - minimum)-3;
//float qvalues=6.0*()
return qvalues;
//qvalues[1] = 3.0 * ecerro / (maximum - minimum);
}
//反区间映射函数
float FuzzyPID::Inverse_quantization(float maximum, float minimum, float qvalues)
{
float x = (maximum - minimum) *(qvalues + 3)/6 + minimum;
return x;
}
测试模糊PID控制器:
#include 运行结果:
本文主要转载了模糊控制原理部分以及代码例程,为了方便管理与收藏发布到CSDN。
原文地址:https://www.codenong.com/cs105632129/