无人驾驶-控制-PID

无人驾驶-控制-PID

一、PID简介

1.1 详解

PID( Proportional Integral Derivative)控制是最早发展起来的控制策略之一，由于其算法简单、鲁棒性好和可靠性高，被广泛应用于工业过程控制，尤其适用于可建立精确数学模型的确定性控制系统。

在工程实际中，应用最为广泛的调节器控制规律为比例、积分、微分控制，简称PID控制，又称PID调节，它实际上是一种算法。PID控制器问世至今已有近70年历史，它以其结构简单、稳定性好、工作可靠、调整方便而成为工业控制的主要技术之一。

当被控对象的结构和参数不能完全掌握，或得不到精确的数学模型时，控制理论的其它技术难以采用时，系统控制器的结构和参数必须依靠经验和现场调试来确定，这时应用PID控制技术最为方便。即当我们不完全了解一个系统和被控对象，或不能通过有效的测量手段来获得系统参数时，最适合用PID控制技术。PID控制，实际中也有PI和PD控制。PID控制器就是根据系统的误差，利用比例、积分、微分计算出控制量进行控制的。

1.2 校正分类

从信号变换的角度而言，超前校正、滞后校正、滞后－超前校正可以总结为比例、积分、微分三种运算及其组合。PID调节器的适用范围：PID调节控制是一个传统控制方法，它适用于温度、压力、流量、液位等几乎所有现场，不同的现场，仅仅是PID参数应设置不同，只要参数设置得当均可以达到很好的效果。均可以达到0.1%，甚至更高的控制要求。

PID控制的不足

1. 在实际工业生产过程往往具有非线性、时变不确定，难以建立精确的数学模型，常规的PID控制器不能达到理想的控制效果；

2. 在实际生产现场中，由于受到参数整定方法烦杂的困扰，常规PID控制器参数往往整定不良、效果欠佳，对运行工况的适应能力很差。

1.3 调节思路

任何闭环控制系统的首要任务是要==稳（稳定）、快（快速）、准（准确）==的响应命令。PID调整的主要工作就是如何实现这一任务。

（1）比例积分系数P的作用

• 增大比例系数P将加快系统的响应，它的作用于输出值较快，但不能很好稳定在一个理想的数值，不良的结果是虽较能有效的克服扰动的影响，但有余差出现，过大的比例系数会使系统有比较大的超调，并产生振荡，使稳定性变坏。

• 积分能在比例的基础上消除余差，它能对稳定后有累积误差的系统进行误差修整，减小稳态误差。微分具有超前作用，对于具有容量滞后的控制通道，引入微分参与控制，在微分项设置得当的情况下，对于提高系统的动态性能指标，有着显著效果，它可以使系统超调量减小，稳定性增加，动态误差减小。

  综上所述，P—比例控制系统的响应快速性，快速作用于输出，好比"现在"（现在就起作用，快），I—积分控制系统的准确性，消除过去的累积误差，好比"过去"（清除过去积怨，回到准确轨道），D—微分控制系统的稳定性，具有超前控制作用，好比"未来"（放眼未来，未雨绸缪，稳定才能发展）。

（2）PID值对应的效果

在调整的时候，你所要做的任务就是在系统结构允许的情况下，在这三个参数之间权衡调整，达到最佳控制效果，实现稳快准的控制特点。

• 比例控制可快速、及时、按比例调节偏差，提高控制灵敏度，但有静差，控制精度低。

• 积分控制能消除偏差，提高控制精度、改善稳态性能，但易引起震荡，造成超调。

• 微分控制是一种超前控制，能调节系统速度、减小超调量、提高稳定性，但其时间常数过大会引入干扰、系统冲击大，过小则调节周期长、效果不显著。

比例、积分、微分控制相互配合，合理选择PID调节器的参数，即比例系数KP、积分时间常数Ti和微分时间常数TD，可迅速、准确、平稳的消除偏差，达到良好的控制效果。

二、PID分类

2.1 比例环节

成比例地反映控制系统的偏差信号e(t)，偏差一旦产生，控制器立即产生控制作用，以减小偏差。当仅有比例控制时系统输出存在稳态误差。

P参数越大比例作用越强，动态响应越快，消除误差的能力越强。但实际系统是有惯性的，控制输出变化后，实际y(t)值变化还需等待一段时间才会缓慢变化。由于实际系统是有惯性的，比例作用不宜太强，比例作用太强会引起系统振荡不稳定。P参数的大小应在以上定量计算的基础上根据系统响应情况，现场调试决定，通常将P参数由大向小调，以能达到最快响应又无超调(或无大的超调)为最佳参数。

• 优点：调整系统的开环比例系数，提高系统的稳态精度，减低系统的惰性，加快响应速度。

• 缺点：仅用P控制器，过大的开环比例系数不仅会使系统的超调量增大，而且会使系统稳定裕度变小，甚至不稳定。

2.2 积分环节

（1）为什么要引进积分作用？

控制器的输出与输入误差信号的积分成正比关系。主要用于消除静差，提高系统的无差度。积分作用的强弱取决于积分时间常数T，T越大，积分作用越弱，反之则越强。

比例作用的输出与误差的大小成正比，误差越大，输出越大，误差越小，输出越小，误差为零，输出为零。由于没有误差时输出为零，因此比例调节不可能完全消除误差，不可能使被控的PV值达到给定值。必须存在一个稳定的误差，以维持一个稳定的输出，才能使系统的PV值保持稳定。这就是通常所说的比例作用是有差调节，是有静差的，加强比例作用只能减少静差，不能消除静差(静差：即静态误差，也称稳态误差)。

为了消除静差必须引入积分作用，积分作用可以消除静差，以使被控的y(t)值最后与给定值一致。

（2）积分消除误差原理？

积分作用消除静差的原理是，只要有误差存在，就对误差进行积分，使输出继续增大或减小，一直到误差为零，积分停止，输出不再变化，系统的PV值保持稳定，y(t)值等于u(t)值，达到无差调节的效果。

但由于实际系统是有惯性的，输出变化后，y(t)值不会马上变化，须等待一段时间才缓慢变化，因此积分的快慢必须与实际系统的惯性相匹配，惯性大、积分作用就应该弱，积分时间I就应该大些，反之而然。如果积分作用太强，积分输出变化过快，就会引起积分过头的现象，产生积分超调和振荡。通常I参数也是由大往小调，即积分作用由小往大调，观察系统响应以能达到快速消除误差，达到给定值，又不引起振荡为准。

对一个自动控制系统，如果在进入稳态后存在稳态误差，则称这个控制系统是有稳态误差的或简称有差系统（System with Steady-state Error）。为了消除稳态误差，在控制器中必须引入“积分项”。积分项对误差取决于时间的积分，随着时间的增加，积分项会增大。这样，即便误差很小，积分项也会随着时间的增加而加大，它推动控制器的输出增大使稳态误差进一步减小，直到等于零。因此，比例+积分(PI)控制器，可以使系统在进入稳态后无稳态误差。PI控制器不但保持了积分控制器消除稳态误差的“记忆功能”，而且克服了单独使用积分控制消除误差时反应不灵敏的缺点。

• 优点：消除稳态误差。

• 缺点：积分控制器的加入会影响系统的稳定性，使系统的稳定裕度减小。

2.3 微分环节

反映偏差信号的变化趋势，并能在偏差信号变得太大之前，在系统中引入一个有效的早期修正信号，从而加快系统的动作速度，减少调节时间。在微分控制中，控制器的输出与输入误差信号的微分（即误差的变化率）成正比关系。

（1）为什么要引进微分作用？

前面已经分析过，不论比例调节作用，还是积分调节作用都是建立在产生误差后才进行调节以消除误差，都是事后调节，因此这种调节对稳态来说是无差的，对动态来说肯定是有差的，因为对于负载变化或给定值变化所产生的扰动，必须等待产生误差以后，然后再来慢慢调节予以消除。

但一般的控制系统，不仅对稳定控制有要求，而且对动态指标也有要求，通常都要求负载变化或给定调整等引起扰动后，恢复到稳态的速度要快，因此光有比例和积分调节作用还不能完全满足要求，必须引入微分作用。比例作用和积分作用是事后调节(即发生误差后才进行调节)，而微分作用则是事前预防控制，即一发现y(t)有变大或变小的趋势，马上就输出一个阻止其变化的控制信号，以防止出现过冲或超调等。

D越大，微分作用越强，D越小，微分作用越弱。系统调试时通常把D从小往大调，具体参数由试验决定。

三、PID整定

PID控制器的参数整定是控制系统设计的核心内容。它是根据被控过程的特性确定PID控制器的比例系数、积分时间和微分时间的大小。PID控制器参数整定的方法很多，概括起来有两大类：

3.1 理论计算整定法

它主要是依据系统的数学模型，经过理论计算确定控制器参数。这种方法所得到的计算数据未必可以直接用，还必须通过工程实际进行调整和修改。

3.2 工程整定方法

它主要依赖工程经验，直接在控制系统的试验中进行，且方法简单、易于掌握，在工程实际中被广泛采用。PID控制器参数的工程整定方法，主要有临界比例法、反应曲线法和衰减法。三种方法各有其特点，其共同点都是通过试验，然后按照工程经验公式对控制器参数进行整定。但无论采用哪一种方法所得到的控制器参数，都需要在实际运行中进行最后调整与完善。现在一般采用的是临界比例法。利用该方法进行 PID控制器参数的整定步骤如下：

• 首先预选择一个足够短的采样周期让系统工作；
• 仅加入比例控制环节，直到系统对输入的阶跃响应出现临界振荡，记下这时比例放大系数和临界振荡周期；
• 在一定的控制度下通过公式计算得到PID控制器的参数。

3.3 PID调试一般原则

• 在输出不振荡时，增大比例增益P。
• 在输出不振荡时，减小积分时间常数Ti。
• 在输出不振荡时，增大微分时间常数Td。

3.4 PID调试一般步骤

（1）确定比例增益P

确定比例增益P 时，首先去掉PID的积分项和微分项，一般是令Ti=0、Td=0（具体见PID的参数设定说明），使PID为纯比例调节。输入设定为系统允许的最大值的60%-70%，由0逐渐加大比例增益P，直至系统出现振荡；再反过来，从此时的比例增益P逐渐减小，直至系统振荡消失，记录此时的比例增益P，设定PID的比例增益P为当前值的70%，比例增益P调试完成。

（2）确定积分时间常数Ti

比例增益P确定后，设定一个较大的积分时间常数Ti的初值，然后逐渐减小Ti，直至系统出现振荡，之后在反过来，逐渐加大Ti，直至系统振荡消失。记录此时的Ti，设定PID的积分时间常数Ti为当前值的150%~180%。积分时间常数Ti调试完成。

（3）确定微分时间常数Td

微分时间常数Td一般不用设定，为0即可。若要设定，与确定 P和Ti的方法相同，取不振荡时的30%。

（4）系统空载、带载联调，再对PID参数进行微调，直至满足要求。

变速积分的基本思想是，设法改变积分项的累加速度，使其与偏差大小相对应：偏差越大，积分越慢；反之则越快，有利于提高系统品质。

四、离散式PID算法

4.1 离散近似处理

上篇介绍了PID，但是计算机控制是一种采样控制，他只能根据采样时刻的偏差来计算控制量，因此计算机控制系统中，必须对公式进行离散化，具体就是用求和代替积分，用向后差分来代替微分，使模拟PID离散化为数字形式的差分方程。

在采样周期足够小时，可以作如下近似：

式中：
T————为采样周期
k————为采样序号，k=0,1,2….
用这种近似方法，可以得到两种形式数字PID控制算法

4.2 位置式PID

由4.1的离散化近似处理可以得到下式：

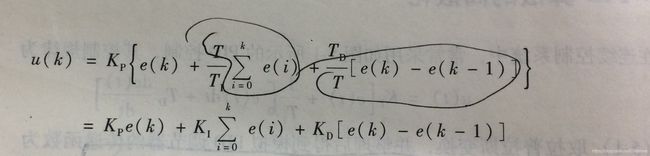
由此式可以看出数字调节的输出u(k)跟过去的所有偏差信号有关，计算机需要对e(i)进行累加，运算量太大，一般不用，重点说明增量式PID算法。

4.3 增量式PID

由于位置式PID的算法不够方便，不仅对偏差进行累加，占用过多的存储单元，而且不方便写程序，所以需要进行一些改进，对位置式取增量，方法如下：

增量式PID采用的是误差量进行计算：

P * (err - last_err) + Ki * err + Kd * [err - 2 * last_err - last_last_err]

只需要记录上一刻和上上时刻的误差，简便了计算机计算。

五、PID动态调参

PID调参除了手动设置Kp,Ki,Kd值，还可以利用ros pid进行动态调参：

rosrun rqt_reconfigure rqt_reconfigure

写一个cfg文件

#!/usr/bin/env python
PACKAGE = "control"

from dynamic_reconfigure.parameter_generator_catkin import *

gen = ParameterGenerator()

gen.add("kp_d", double_t, 0, "kpd", 0.3, -10, 10);
gen.add("ki_d", double_t, 0, "ki_d", 0.00012, -10, 10);
gen.add("kd_d", double_t, 0, "kd_d", 3, -10, 10);

exit(gen.gennerate(PACKAGE, "control", "control"));

六、PID代码实现

6.1 位置式PID

	/*位置式pid*/
    /**
     * 速度反馈的PID纵向控制：返回车辆加速度
     * @param _Kp @param _Ki @param _Kd PID
     * @param _expSpd                   期望速度
     * @param _spdErr                   速度差 （期望速度-当前速度）
     * @param _spdDiff                  速度差的微分
     * @param _spdErrSum                速度差的积分
     * @param _preAccel                 上一时刻的加速度量
    */
    double PID_Controller::longitudeControl( double _expSpd, double _spdErr, double _spdDiff, double _spdErrSum, double _preAccel)
    {
        double accel = 0;
      
        double tmpAccel = Kp * _spdErr + Kd * _spdDiff + Ki * _spdErrSum;
        
        return tmpaccel;
    }

	double spdErr = expected_speed - curSpd;            // 速度差，速度差积分，速度差微分
	double spdErrSum = preSpdErrSum + spdErr;
	double spdDiff = spdErr - preSpdErr;
	
	double preAccel = Cmd.accel;                // 上一时刻加速度量
	
	// 更新当前的控制量
	double tmp = longitudeControl(1.0, spdErr, spdDiff, spdErrSum, preAccel);

6.2 增量式PID

	/*增量式PID*/
    double PID_Controller::longitudeControl(double target, double current, double &err_last, double &err_last_last, double &voltage)
    {
        double Kp;
        double Ki;
        double Kd; //定义比例、积分、微分系数
        double err = target - current;
        double increment = Kp * (err - err_last) + Ki * err + Kd * (err - 2 * err_last + err_last_last);
        voltage += increment;
        err_last = err;
        err_last_last = err_last;
        return voltage;
    }

七、参考链接

1. https://blog.csdn.net/tingfenghanlei/article/details/85028677
2. https://charmve.blog.csdn.net/article/details/104537081