题目描述
这是 LeetCode 上的 149. 直线上最多的点数 ,难度为 困难。
Tag : 「数学」、「枚举」、「哈希表」
给你一个数组 points,其中 $points[i] = [x_i, y_i]$ 表示 X-Y 平面上的一个点。求最多有多少个点在同一条直线上。
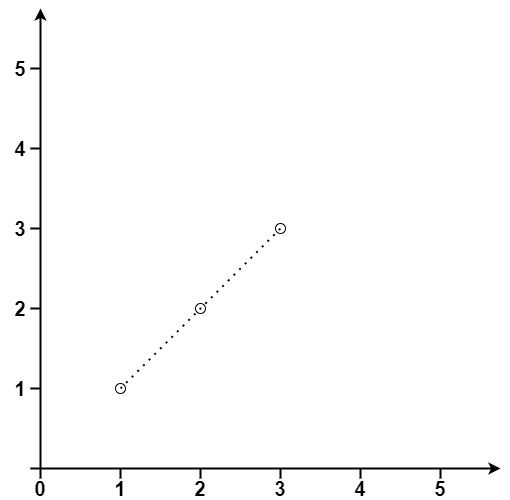
输入:points = [[1,1],[2,2],[3,3]]
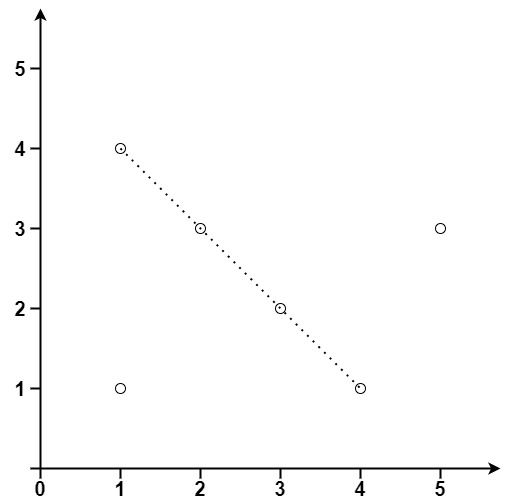
输出:3输入:points = [[1,1],[3,2],[5,3],[4,1],[2,3],[1,4]]
输出:4提示:
- $1 <= points.length <= 300$
- $points[i].length == 2$
- $-10^4 <= x_i, y_i <= 10^4$
points中的所有点 互不相同
模拟(枚举直线 + 枚举统计)
我们知道,两个点可以确定一条线。
因此一个朴素的做法是先枚举两条点(确定一条线),然后检查其余点是否落在该线中。
为了避免除法精度问题,当我们枚举两个点 $i$ 和 $j$ 时,不直接计算其对应直线的 斜率和 截距,而是通过判断 $i$ 和 $j$ 与第三个点 $k$ 形成的两条直线斜率是否相等(斜率相等的两条直线要么平行,要么重合,平行需要 $4$ 个点来唯一确定,我们只有 $3$ 个点,所以可以直接判定两直线重合)。
代码:
class Solution {
public int maxPoints(int[][] ps) {
int n = ps.length;
int ans = 1;
for (int i = 0; i < n; i++) {
int[] x = ps[i];
for (int j = i + 1; j < n; j++) {
int[] y = ps[j];
int cnt = 2;
for (int k = j + 1; k < n; k++) {
int[] p = ps[k];
int s1 = (y[1] - x[1]) * (p[0] - y[0]);
int s2 = (p[1] - y[1]) * (y[0] - x[0]);
if (s1 == s2) cnt++;
}
ans = Math.max(ans, cnt);
}
}
return ans;
}
}- 时间复杂度:$O(n^3)$
- 空间复杂度:$O(1)$
优化(枚举直线 + 哈希表统计)
根据「朴素解法」的思路,枚举所有直线的过程不可避免,但统计点数的过程可以优化。
具体的,我们可以先枚举所有可能出现的 直线斜率(根据两点确定一条直线,即枚举所有的「点对」),使用「哈希表」统计所有 斜率 对应的点的数量,在所有值中取个 $max$ 即是答案。
一些细节:在使用「哈希表」进行保存时,为了避免精度问题,我们直接使用字符串进行保存,同时需要将 斜率 约干净。
代码:
class Solution {
public int maxPoints(int[][] ps) {
int n = ps.length;
int ans = 1;
for (int i = 0; i < n; i++) {
Map map = new HashMap<>();
// 由当前点 i 发出的直线所经过的最多点数量
int max = 0;
for (int j = i + 1; j < n; j++) {
int x1 = ps[i][0], y1 = ps[i][1], x2 = ps[j][0], y2 = ps[j][1];
int a = x1 - x2, b = y1 - y2;
int k = gcd(a, b);
String key = (a / k) + "_" + (b / k);
map.put(key, map.getOrDefault(key, 0) + 1);
max = Math.max(max, map.get(key));
}
ans = Math.max(ans, max + 1);
}
return ans;
}
int gcd(int a, int b) {
return b == 0 ? a : gcd(b, a % b);
}
} - 时间复杂度:枚举所有直线的复杂度为 $O(n^2)$;令坐标值的最大差值为 $m$,
gcd复杂度为 $O(\log{m})$。整体复杂度为 $O(n^2 \times \log{m})$ - 空间复杂度:$O(n)$
最后
这是我们「刷穿 LeetCode」系列文章的第 No.149 篇,系列开始于 2021/01/01,截止于起始日 LeetCode 上共有 1916 道题目,部分是有锁题,我们将先把所有不带锁的题目刷完。
在这个系列文章里面,除了讲解解题思路以外,还会尽可能给出最为简洁的代码。如果涉及通解还会相应的代码模板。
为了方便各位同学能够电脑上进行调试和提交代码,我建立了相关的仓库:https://github.com/SharingSou... 。
在仓库地址里,你可以看到系列文章的题解链接、系列文章的相应代码、LeetCode 原题链接和其他优选题解。
更多更全更热门的「笔试/面试」相关资料可访问排版精美的 合集新基地
本文由mdnice多平台发布