语义分割基础知识

1. 常见的分割任务

1. 语义分割 (Semantic Segmentation) -> FCN
2. 实例分割 (Instance Segmentation) -> Mask R-CNN
3. 全景分割 (Panoramic Segmentation) -> Panoptic FPN

2. 暂定的学习规划

Model	mIoU	Global Pixel Acc	Inference on CPU (sec)	Params (M)
LR-ASPP MobileNetV3-Large	57.9	91.2	0.3278	3.22
DeepLabV3 MobileNetV3-Large	60.3	91.2	0.5869	11.03
FCN MobileNetV3-Large (not released)	57.8	90.9	0.3702	5.05
DeepLabV3 ResNet50	66.4	92.4	6.3531	39.64
FCN ResNet50	60.5	91.4	5.0146	32.96

3. 语义分割任务常见数据格式

3.1 PASCAL VOC

PASCAL VOC中提供了分割数据集, 数据集中的图片对应标签存储格式为PNG (如右图所示), 标签图片中记录了每一个像素所属的类别信息. 需要注意的是, 右图所展示的图片是使用调色板实现的彩色, 它本质上是一个单通道的黑白图片.

那么这样是怎么实现的呢? 我们知道, 黑白图片每个像素的范围为 0 ~ 255, 那么不同值的像素就对应不同的颜色. 比如:

• 像素0对应的是 (0, 0, 0) -> 黑色
• 像素1对应的是 (127, 0, 0) -> 深红色
• 像素255对应的是 (224, 224, 129) -> 灰色(特殊颜色)

这样, 不同值的像素就可以对应不同的颜色, 那么一张单通道黑白图就可以显示出彩色.

在使用Python的PIL读取灰度图时, 默认使用调色板, 即P模式.

除了上述需要明白的, 还有一些需要注意的点:

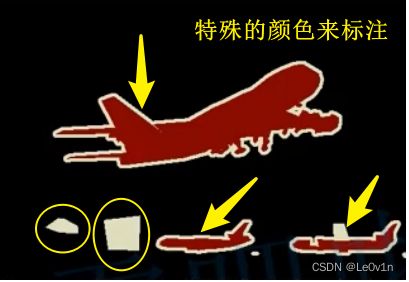
1. 目标的边缘会用特殊的颜色进行区分
2. 图片中的特殊区域也会用该颜色进行填充

特殊颜色标注位置对应像素的值是255, 在网络训练时, Loss的计算会忽略像素值为255的地方, 这么做的原因是:

1. 对于目标边缘到底属于那个部分, 并不好区分.
2. 对于一些不好分割的目标, 使用该颜色进行填充, 以降低难度

3.2 MS COCO

MS COCO数据集针对图像中的每一个目标都记录了多边形坐标 (polygons)

可以看到, COCO中所有目标的轮廓都用多边形坐标展示出来了, 在使用MS COCO数据集时, 我们需要将多边形信息解码为PNG图片 (所期望的P模式PNG图片).

因为COCO划分的过于详细, 所以数据集不光可以做语义分割, 还可以做实例分割.

4. 语义分割得到结果的具体形式

用调色板是方便看, 不然真的用灰度图的话, 0 ~ 255, 人眼很难区分的.

5. 常见语义分割评价指标

$$\begin{array}{rl}& \mathrm{Pixel}\mathrm{Accuracy}(\mathrm{Global}\mathrm{Acc})=\frac{{\sum }_i{n}_{ii}}{{\sum }_i{t}_i}\\ & \mathrm{mean}\mathrm{Accuracy}=\frac{1}{n_{cls}}\cdot \sum _i\frac{n_{ii}}{t_i}\\ & \mathrm{mean}\mathrm{IoU}=\frac{1}{n_{cls}}\cdot \sum _i\frac{n_{ii}}{t_i+{\sum }_j{n}_{ji}-n_{ii}}\end{array}$$

其中:

• $n_{ii}$: 类别 $i$ 被预测为类别 $i$ 的像素个数 (预测正确的像素个数)
• $n_{ij}$: 类别 $i$ 被预测为类别 $j$ 的像素个数 (预测错误的像素个数)
• $n_{cls}$: 目标类别个数 (包含背景)
• $t_i={\sum }_j{n}_{ij}$: 目标类别 $i$ 的总像素个数 (真实标签)

---

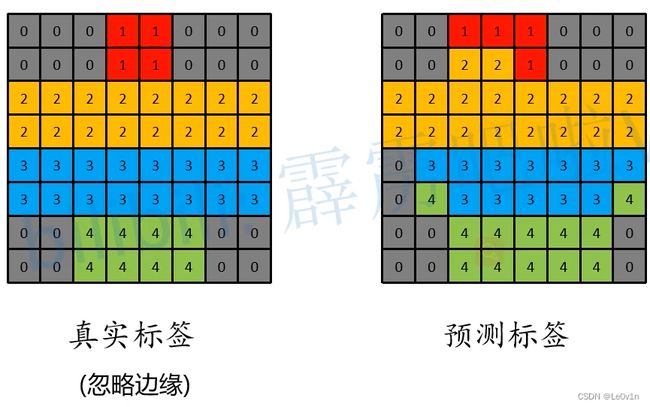
因为忽略了边缘, 所以没有255的情况

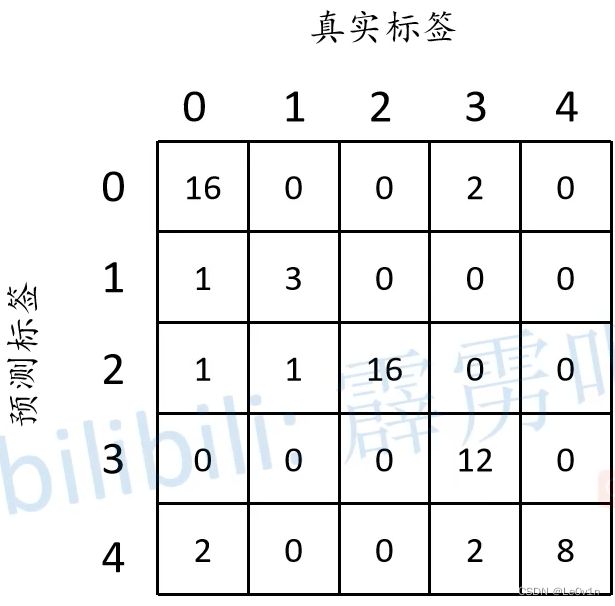
针对每一个类别, 分别计算正负样本, 即可得到混淆矩阵, 如下图所示:

根据混淆矩阵就可以得到Global Accuracy (Pixel Accuracy):

$$\mathrm{Pixel}\mathrm{Accuracy}(\mathrm{Global}\mathrm{Acc})=\frac{16+3+16+12+8}{64}\approx 0.859$$

也可以根据每一个类别算出不同类别的Accuracy:

$$\begin{array}{rl}& \mathrm{cl}{\mathrm{s}}_0\mathrm{acc}=\frac{16}{20}\\ & \mathrm{cl}{\mathrm{s}}_1\mathrm{acc}=\frac{3}{4}\\ & \mathrm{cl}{\mathrm{s}}_2\mathrm{acc}=\frac{16}{16}\\ & \mathrm{cl}{\mathrm{s}}_3\mathrm{acc}=\frac{12}{16}\\ & \mathrm{cl}{\mathrm{s}}_4\mathrm{acc}=\frac{8}{8}\end{array}$$

也就是混淆矩阵对角线上的值分别除以它们各自的数量 (标签中该类别的数量)

得到了所有类别各自的Accuracy, 也就可以得的mean Accuracy:

$$\begin{array}{rl}\mathrm{mean}\mathrm{Accuracy}& =\frac{1}{n_{cls}}\cdot \sum _i\frac{n_{ii}}{t_i}\\ & \frac{\frac{16}{20}+\frac{3}{4}+\frac{16}{16}+\frac{12}{16}+\frac{8}{8}}{5}\\ & =0.86\end{array}$$

根据公式:

$$\begin{array}{rl}\mathrm{mean}\mathrm{IoU}& =\frac{1}{n_{cls}}\cdot \sum _i\frac{n_{ii}}{t_i+{\sum }_j{n}_{ji}-n_{ii}}\\ & \frac{预测对的该类别像素个数}{预测为该类别的像素个数+该类别标签中的个数(因该预测对的个数)-预测对的该类别像素个数}\end{array}$$

其中:

• 预测对的该类别像素个数: 对角线
• 预测为该类别的像素个数: 列
• 该类别标签中的个数(因该预测对的个数): 行

因此, 我们就可以计算出mean IoU:

$$\begin{array}{rl}& {\mathrm{mean}\mathrm{IoU}}_{cl{s}_0}=\frac{16}{20+18-16}\\ & {\mathrm{mean}\mathrm{IoU}}_{cl{s}_1}=\frac{3}{4+4-3}\\ & {\mathrm{mean}\mathrm{IoU}}_{cl{s}_2}=\frac{16}{16+18-16}\\ & {\mathrm{mean}\mathrm{IoU}}_{cl{s}_3}=\frac{12}{16+12-12}\\ & {\mathrm{mean}\mathrm{IoU}}_{cl{s}_4}=\frac{8}{8+12-8}\end{array}$$

6. 语义分割标注工具

6.1 Labelme -> 纯手工

代码地址: https://github.com/wkentaro/labelme

6.2 EISeg -> 半自动

代码地址: https://github.com/PaddlePaddle/PaddleSeg

该标注软件是一个半自动的标注工具, 里面内置了一些预训练模型, 可以使用AI帮助我们标注.

百度的标注工具对于日常中常见的目标来说, 是极为高效的, 如果自定义数据集中的目标相对罕见, 那么EISeg和Labelme其实是差不多的.

参考

1. https://www.bilibili.com/video/BV1ev411P7dR