【数据分析系列】Python数据预处理总结篇

1.缺失值处理

• 数据缺失主要包括记录缺失和字段信息缺失等情况，其对数据分析会有较大影响，导致结果不确定性更加显著
• 缺失值的处理：删除记录 / 数据插补 / 不处理

import warnings
warnings.filterwarnings('ignore')
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy import stats

# 判断是否有缺失值数据 - isnull，notnull
# isnull：缺失值为True，非缺失值为False
# notnull：缺失值为False，非缺失值为True

s = pd.Series([12,33,45,23,np.nan,np.nan,66,54,np.nan,99])
df = pd.DataFrame({'value1':[12,33,45,23,np.nan,np.nan,66,54,np.nan,99,190],
                  'value2':['a','b','c','d','e',np.nan,np.nan,'f','g',np.nan,'g']})
#查看缺失值
print(s.isnull())

print(df.isnull().sum())

1.1删除缺失值dropna

# 删除缺失值 - dropna
s.dropna(inplace=True)
df1=df[['value1','value2']].dropna()
print(df1.isnull().sum())

1.2填充/替换缺失数据 - fillna、replace

#用0来填补缺失值
s.fillna(0,inplace=True)

#用缺失值之前/之后的数填充
df['value1'].fillna(method='pad',inplace=True)
# method参数：
# pad / ffill → 用之前的数据填充 
# backfill / bfill → 用之后的数据填充 
# print(df['value1'])

#替换缺失值
df['value2'].replace([1,2,3],np.nan,inplace=True)

1.3缺失值插补(mean,median,mode,ffill,lagrange)

# 缺失值插补
# 几种思路：均值/中位数/众数插补、临近值插补、插值法
# （1）均值/中位数/众数插补

# 分别求出均值/中位数/众数
u = s.mean()     # 均值
me = s.median()  # 中位数
mod = s.mode()   # 众数
print('均值为：%.2f, 中位数为：%.2f' % (u,me))
print('众数为：', mod.tolist())
print('------')


# 用均值填补
s.fillna(u,inplace = True)
print(s)

#用中位数填补
s.fillna(me,inplace = True)
print(s)

#用众数填补
s.fillna(mod,inplace = True)
print(s)

#临近值填补
#用前值插补
s.fillna(method='ffill',inplace=True)

#拉格朗日插值法
from scipy.interpolate import lagrange
data = pd.Series(np.random.rand(100)*100)
data[3,6,33,56,45,66,67,80,90] = np.nan
print(data.head())
print('总数据量:%i' % len(data))
print('------')
# 创建数据

data_na = data[data.isnull()]
print('缺失值数据量:%i' % len(data_na))
print('缺失数据占比:%.2f%%' % (len(data_na) / len(data) * 100))
# 缺失值的数量

data_c = data.fillna(data.median())  #  中位数填充缺失值
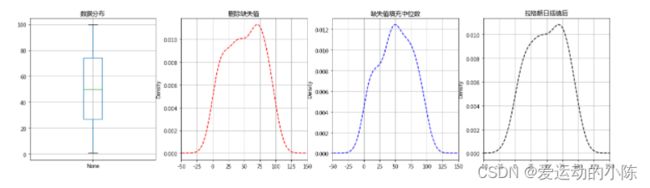
fig,axes = plt.subplots(1,4,figsize = (20,5))
data.plot.box(ax = axes[0],grid = True,title = '数据分布')
data.plot(kind = 'kde',style = '--r',ax = axes[1],grid = True,title = '删除缺失值',xlim = [-50,150])
data_c.plot(kind = 'kde',style = '--b',ax = axes[2],grid = True,title = '缺失值填充中位数',xlim = [-50,150])
# 密度图查看缺失值情况

def na_c(s,n,k=5):
    y = s[list(range(n-k,n+1+k))] # 取数
    y = y[y.notnull()]  # 剔除空值
    return(lagrange(y.index,list(y))(n))
# 创建函数，做插值，由于数据量原因，以空值前后5个数据（共10个数据）为例做插值

na_re = []
for i in range(len(data)):
    if data.isnull()[i]:
        data[i] = na_c(data,i)
        print(na_c(data,i))
        na_re.append(data[i])
data.dropna(inplace=True)  # 清除插值后仍存在的缺失值
data.plot(kind = 'kde',style = '--k',ax = axes[3],grid = True,title = '拉格朗日插值后',xlim = [-50,150])
print('finished!')
# 缺失值插值

2.异常值处理

• 异常值是指样本中的个别值，其数值明显偏离其余的观测值
• 异常值也称离群点，异常值的分析也称为离群点的分析
• 异常值分析 → 3σ原则 / 箱型图分析
• 异常值处理方法 → 删除 / 修正填补

2.1 3σ原则

import statsmodels as stats
# 异常值分析
# （1）3σ原则：如果数据服从正态分布，异常值被定义为一组测定值中与平均值的偏差超过3倍的值 → p(|x - μ| > 3σ) ≤ 0.003

data = pd.Series(np.random.randn(10000)*100)
u = data.mean()  # 计算均值
std = data.std()  # 计算标准差

print('均值为：%.3f，标准差为：%.3f' % (u,std))

#正态性检验
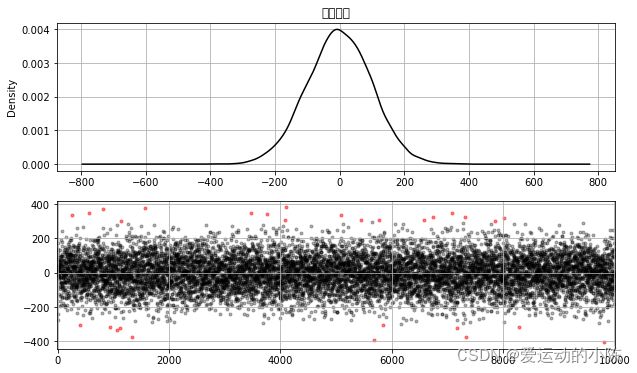
fig=plt.figure(figsize=(10,6))
ax1=fig.add_subplot(2,1,1)

# 绘制数据密度曲线
data.plot(kind = 'kde',grid = True,style = '-k',title = '密度曲线')

ax2=fig.add_subplot(2,1,2)
error=data[np.abs(data-u)>3*std]
data_c=data[np.abs(data-u)<=3*std]
print("异常值共%d条"%(len(error)))

# 筛选出异常值error、剔除异常值之后的数据data_c
plt.scatter(data_c.index,data_c,color = 'k',marker='.',alpha = 0.3)
plt.scatter(error.index,error,color = 'r',marker='.',alpha = 0.5)
plt.xlim([-10,10010])
plt.grid()
# 图表表达

均值为：0.840，标准差为：99.366

异常值共27条

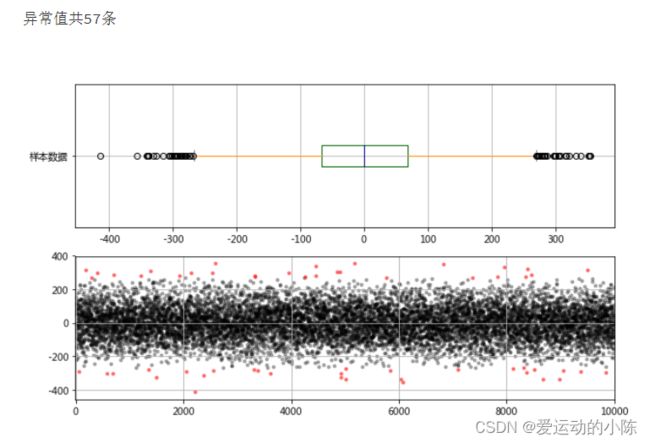
2.2箱型图分析

# 异常值分析
# （2）箱型图分析

fig = plt.figure(figsize = (10,6))
ax1 = fig.add_subplot(2,1,1)
color = dict(boxes='DarkGreen', whiskers='DarkOrange', medians='DarkBlue', caps='Gray')
data.plot.box(vert=False, grid = True,color = color,ax = ax1,label = '样本数据')
# 箱型图看数据分布情况
# 以内限为界

s = data.describe()
print(s)
print('------')
# 基本统计量

q1 = s['25%']
q3 = s['75%']
iqr = q3 - q1
mi = q1 - 1.5*iqr
ma = q3 + 1.5*iqr
print('分位差为：%.3f，下限为：%.3f，上限为：%.3f' % (iqr,mi,ma))
print('------')
# 计算分位差

ax2 = fig.add_subplot(2,1,2)
error = data[(data < mi) | (data > ma)]
data_c = data[(data >= mi) & (data <= ma)]
print('异常值共%i条' % len(error))
# 筛选出异常值error、剔除异常值之后的数据data_c

plt.scatter(data_c.index,data_c,color = 'k',marker='.',alpha = 0.3)
plt.scatter(error.index,error,color = 'r',marker='.',alpha = 0.5)
plt.xlim([-10,10010])
plt.grid()
# 图表表达

3.数据归一化和标准化

数据的标准化（normalization）是将数据按比例缩放，使之落入一个小的特定区间。

在某些比较和评价的指标处理中经常会用到，去除数据的单位限制，将其转化为无量纲的纯数值，便于不同单位或量级的指标能够进行比较和加权.

最典型的就是数据的归一化处理，即将数据统一映射到[0,1]区间上

3.1 0-1标准化

df = pd.DataFrame({"value1":np.random.rand(10)*20,
                  'value2':np.random.rand(10)*100})

#创建函数，标准化数据
def data_norm(df,*cols):
    df_n = df.copy()
    for col in cols:
        ma = df_n[col].max()
        mi = df_n[col].min()
        df_n[col + '_n'] = (df_n[col] - mi) / (ma - mi)
    return(df_n)
# 创建函数，标准化数据

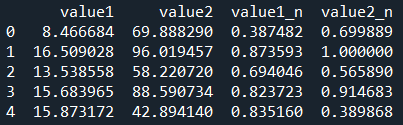
df_n = data_norm(df,'value1','value2')
print(df_n.head())

3.2 Z-score标准化

# 数据标准化
# （2）Z-score标准化
# Z分数（z-score）,是一个分数与平均数的差再除以标准差的过程 → z=(x-μ)/σ，其中x为某一具体分数，μ为平均数，σ为标准差
# Z值的量代表着原始分数和母体平均值之间的距离，是以标准差为单位计算。在原始分数低于平均值时Z则为负数，反之则为正数
# 数学意义：一个给定分数距离平均数多少个标准差?
from  sklearn import preprocessing
df = pd.DataFrame({"value1":np.random.rand(10) * 100,
                  'value2':np.random.rand(10) * 100})
# print(df.head())
# print('------')
# 创建数据

def data_Znorm(df, *cols):
    df_n = df.copy()
    for col in cols:
        u = df_n[col].mean()
        std = df_n[col].std()
        df_n[col + '_Zn'] = (df_n[col] - u) / std
    return(df_n)
# 创建函数，标准化数据

#或者直接用scale函数
dd=preprocessing.scale(df)


print(dd)
df_z = data_Znorm(df,'value1','value2')
u_z = df_z['value1_Zn'].mean()
std_z = df_z['value1_Zn'].std()
print(df_z)
print('标准化后value1的均值为:%.2f, 标准差为：%.2f' % (u_z, std_z))
# 标准化数据
# 经过处理的数据符合标准正态分布，即均值为0，标准差为1

# 什么情况用Z-score标准化：
# 在分类、聚类算法中，需要使用距离来度量相似性的时候，Z-score表现更好

4.数据连续属性离散化(cut,qcut)

连续属性变换成分类属性，即连续属性离散化

在数值的取值范围内设定若干个离散划分点，将取值范围划分为一些离散化的区间，最后用不同的符号或整数值代表每个子区间中的数据值。

4.1等宽法(cut)

# 等宽法 → 将数据均匀划分成n等份，每份的间距相等
# cut方法
ages=[20,22,25,27,21,23,37,31,61,45,41,32]
df=pd.DataFrame({'ages':ages})
# 有一组人员年龄数据，希望将这些数据划分为“18到25”,“26到35”,“36到60”,“60以上”几个面元
bins = [18,25,35,60,100]
group_names=['Youth','YoungAdult','MiddleAged','Senior']
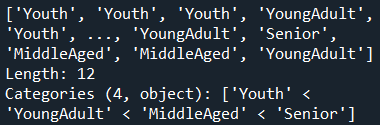
cats=pd.cut(ages,bins=bins,labels=group_names)
cut_counts = s.value_counts(sort=False) 
# print(cats.categories, type(cats.categories))
print(cats)

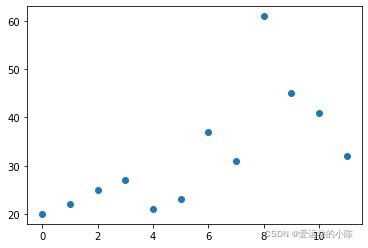
plt.scatter(df.index,df.values)

4.2等频法(qcut)

# 等频法 → 以相同数量的记录放进每个区间
# qcut方法
data = np.random.randn(1000)
s = pd.Series(data)
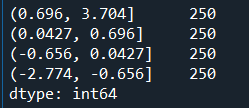
cats=pd.qcut(s,4)# 按四分位数进行切割
print(pd.value_counts(cats))
# qcut → 根据样本分位数对数据进行面元划分，得到大小基本相等的面元，但并不能保证每个面元含有相同数据个数
# 也可以设置自定义的分位数（0到1之间的数值，包含端点） → pd.qcut(data1,[0,0.1,0.5,0.9,1])

plt.scatter(s.index,s,cmap = 'Greens',c = pd.qcut(data,4).codes)
plt.xlim([0,1000])
plt.grid()
# 用散点图表示，其中颜色按照codes分类
# 注意codes是来自于Categorical对象

5.查看数据(info,describle,enumerate,iloc,loc)

import pandas as pd
import numpy as np
test_dict = {'id':[1,2,3,4,5,6],'name':['Alice','Bob','Cindy','Eric','Helen','Grace '],'math':[90,89,99,78,97,93],'english':[89,94,80,94,94,90]}
df = pd.DataFrame(test_dict)
#显示 dataframe 的简明摘要，包括每列非空值的数量
df.info()

# 返回每列数据的有效描述性统计
df.describe()

# 查看每列的索引号和标签
for i, v in enumerate(df.columns):
    print(i, v)


# 这两个函数都是用来找数据框里数据的函数，简单来说是他们的区别
# loc[]传入的是行、列的名字：如loc[‘第几行’,'那一列’]
# iloc[]传入的是行、列的索引：如iloc[1,1]就是第二行第二列
# ps: ':'表示所有的行或列
# 选择从 'id' 到'math.间所有列
df_means = df.loc[:,'id':'math']  #也可用索引号来实现iloc[:,:12]
df_means.head(3)

6.数据冗余(duplicated,drop_duplicates)

import pandas as pd
import numpy as np
test_dict = {'id':[1,2,3,4,5,6,6],'name':['Alice','Bob','Cindy','Eric','Helen','Grace','Grace'],'math':[90,89,99,78,97,93,93],'english':[89,94,80,94,94,90,90]}
df = pd.DataFrame(test_dict)

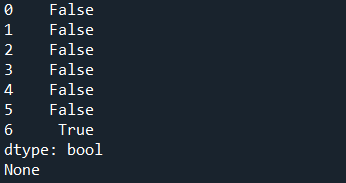
#查看冗余行
print(df.duplicated())

#删除冗余行
print(df.drop_duplicates(inplace=True))

7.表与表的连接(merge,concat,append)

import pandas as pd
import numpy as np
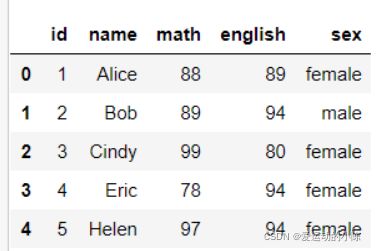
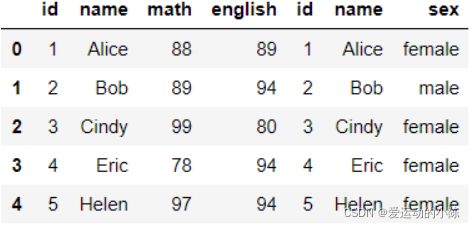
test_dict1 = {'id':[1,2,3,4,5,6],'name':['Alice','Bob','Cindy','Eric','Helen','Grace '],'math':[88,89,99,78,97,93],'english':[89,94,80,94,94,90]}
df1 = pd.DataFrame(test_dict1)
test_dict2 = {'id':[1,2,3,4,5,6],'name':['Alice','Bob','Cindy','Eric','Helen','Grace '],'sex':['female','male','female','female','female','female']}
df2 = pd.DataFrame(test_dict2)

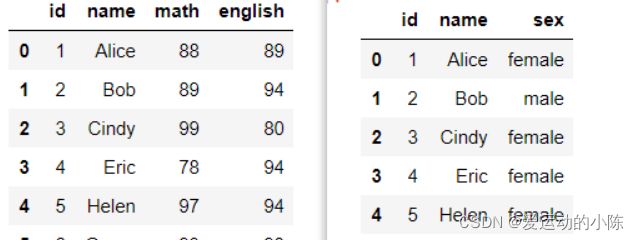
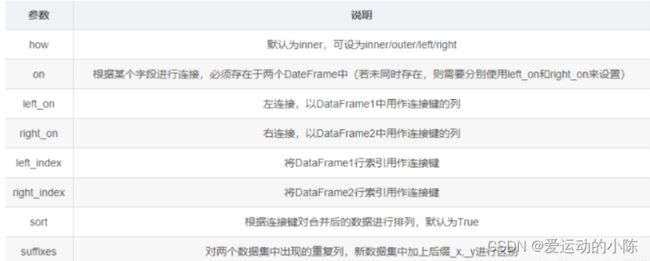
merge函数,默认情况下，会按照相同字段的进行连接,其他参数一般用不到，主要只能两两拼接

df1.merge(df2)

concat()函数

pd.concat(objs, # 要合并对象
		axis=0, # 选择合并轴,0按列，1按行
		join='outer', # 连接方式,默认并集
		join_axes=None, #参数 join_axes 可指定 index 来对齐数据。这样会切掉指定的 index 之外的数据
		ignore_index=False, #当设为 ignore_index=True 时，新 df 将不会使用拼接成员 df 的 index，而是重新生成一个从 0 开始的 index 值
        keys=None, 
        levels=None, 
        names=None, 
        verify_integrity=False,
        copy=True
          )
pd.concat([df1,df2],axis=1)

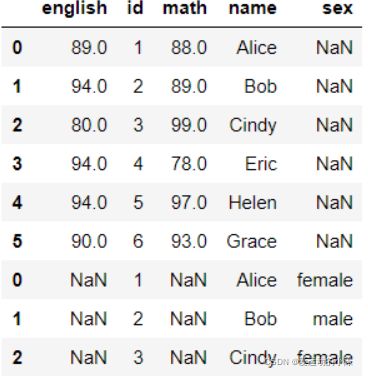
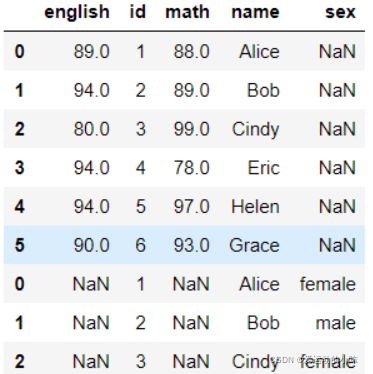
pd.concat([df1,df2],axis=0)

append函数将被 append 的对象添加到调用者的末尾（类似 list 的方法）

DataFrame.append(other, 
				ignore_index=False, 
				verify_integrity=False, 
				sort=None
				)
df1.append(df2)

8.改变数据类型(dtype,astype)

def downcast_dtypes(df):
    cols_float = [c for c in df if df[c].dtype == 'float66']
    cols_object = [c for c in df if df[c].dtype == 'object']
    cols_int64_32 = [c for c in df if df[c].dtype in ['int64', 'int32']]
    df[cols_float] = df[cols_object].astype(np.float32)
    df[cols_object] = df[cols_object].astype(np.float32)
    df[cols_int64_32] = df[cols_int64_32].astype(np.int16)
    return df

9.数据分组聚合(groupby)

data.groupby(by=‘列名’).mean()
  聚合函数：将一组数据进行计算返回一个值agg()是进行聚合操作
  data.groupby(by=‘月份’)[‘最高温度’].max()

  agg_dict={‘最高温度’:[‘max’,‘mean’],‘最低温度’:‘min’}
  data.groupby(by=‘月份’).agg(agg_dict)

def top(month):
  return month.sort_values(by=‘最高温度’)[-2:]
df.groupby(by=‘月份’,sort = False).apply(top)

10.数据抽取与拆分

# # 数据抽取，只有字符型的数据才能抽取
# import pandas
# data=pandas.read_csv(
#   'D:/python/字段拆分.csv',
#    engine='python',encoding='utf-8'
# )
# #将字符型的电话号码列转换成字符型
# data['tel']=data['tel'].astype(str)
# bands=data['tel'].str.slice(0,3)
# nums=data['tel'].str.slice(7,11)
# data['bands']=bands
# data['nums']=nums

# # 按字符串拆分
# # str.split(str="",num=string.count(str))[n]
# # num表示分割次数
# newdata=data['name'].str.split(' ',1,True)
# # 重命名每一列的名字
# newdata.columns=['bands','name']


# # 时间数据抽取
# data['时间']=pandas.to_datetime(data.注册时间,format='%Y/%m%d %H:%M:%S')#将注册时间转换为实践类型的数据然后赋值给时间列
# data['时间.年']=data['时间'].dt.year
# data['时间.月']=data['时间'].dt.month
# data['时间.日']=data['时间'].dt.day
# data['时间.时']=data['时间'].dt.hour
# data['时间.分']=data['时间'].dt.minute
# data['时间.秒']=data['时间'].dt.second

#DataFrame[condition]
#比较
df[df.comments>10000] 
#范围
between(left,right)
df[df.comments.between(1000,10000)]  
#空值匹配
pandas.isnull(column)  #判断是否有空值
df[pandas.isnull(df.title)
#字符匹配
str.contains(patten,na=False) #空值的处理方式,空值不匹配(False)
如:df[df.title.str.contains("台电",na=False)]
#逻辑运算(与&,或|,取反not)
如:df[(df.comments>=1000)&(df.comments<=10000)]
等价于df[df.comments.between(1000,10000)]