2022宁夏杯B题思路分析+代码(大学生就业问题分析)
2022宁夏杯B题完整题目:
链接:https://pan.baidu.com/s/1aClw5k-Ux-17rckTIRWrdg?pwd=1234
提取码:1234
文章目录
- 一、题目
- 二、数据预处理
- 三、第一问
-
- 1、方法一:绘制图形
- 2、方法二:多元线性回归
- 3、方法三:多因素方差分析
- 4、方法四:决策树
- 四、第二问
-
- 1、回归关系
- 2、薪水预测
- 五、第三问
一、题目
大学生就业问题一直是社会关注的焦点。据此前教育部新闻发布会通报, 2022 届高校毕业生规模达 1076 万人,首次突破 1000 万人,规模和增量均创下 了历史新高。同时受市场环境和疫情等因素的影响,就业压力较大。大学生就业 呈现出哪些特征和趋势呢?在众多就业的学生中,是什么样的因素决定了部分学 生在众多的竞争中获得了薪水不同的工作?这些因素可能包括大学的成绩、本身 的技能、大学与工业中心的接近程度、拥有的专业化程度、特定行业的市场条件等。 据悉,印度共有 6214 所工程和技术院校,其中约有 290 万名学生。每年平 均有 150 万学生获得工程学学位,但由于缺乏从事技术工作所需的技能,只有不 到 20% 的 学 生 在 其 核 心 领 域 找 到 工 作 。 附 件 (https://www.datafountain.cn/datasets/4955)给出了印度工程类专业毕业生就业的工资水平和各因素情况表。
根据附件数据结合其他资料研究:
(1) 分析影响高校工程类专业毕业生就业的主要因素。
(2) 根据附件一建立模型,刻画工程类专业毕业生薪水和各因素的关系。
(3) 根据以上的分析,对我国高校工程类专业学生培养是否有一定的启迪? 如果有,请为你所在的高校写一份咨询建议。
| 属性 | 说明 |
|---|---|
| ID | 用于识别候选人的唯一ID |
| 薪金 | 向候选人提供的年度CTC(以INR为单位) |
| 性别 | 候选人的性别 |
| DOB | 候选人的出生日期 |
| 10% | 在10年级考试中获得的总成绩 |
| 10board | 10年级时遵循其课程的校务委员会 |
| 12毕业 | 毕业年份-高中 |
| 12% | 在12年级考试中获得的总成绩 |
| 12board | 候选人遵循其课程的校务委员会 |
| CollegeID | 唯一ID,用于标识候选人为其大学就读的大学/学院 |
| CollegeTier | 每所大学都被标注为1或2。标注是根据该学院/大学学生获得的平均AMCAT分数计算得出的。平均分数高于阈值的大学被标记为1,其他被标记为2。 |
| 学位 | 候选人获得/追求的学位 |
| 专业化 | 候选人追求的专业化 |
| CollegeGPA | 毕业时的GPA总计 |
| CollegeCityID | 唯一的ID,用于标识学院所在的城市。 |
| CollegeCityTier | 学院所在城市的层。这是根据城市人口进行注释的。 |
| CollegeState | 学院所在州的名称 |
| 毕业年份 | 毕业年份(学士学位) |
| 英语 | AMCAT英语部分中的分数 |
| 逻辑 | 在AMCAT逻辑能力部分中得分 |
| 数量 | 在AMCAT的“定量能力”部分中得分 |
| 域 | AMCAT域模块中的分数 |
| ComputerProgramming | AMCAT的“计算机编程”部分中的得分 |
| ElectronicsAndSemicon | AMCAT的“电子和半导体工程”部分得分 |
| 计算机科学 | 在AMCAT的“计算机科学”部分中得分 |
| MechanicalEngg | AMCAT机械工程部分中的得分 |
| ElectricalEngg | AMCAT的电气工程部分中的得分 |
| TelecomEngg | AMCAT的“电信工程”部分中的得分 |
| CivilEngg | AMCAT的“土木工程”部分中的得分 |
| 尽职调查 | AMCAT人格测验之一的分数 |
| 一致性 | AMCAT人格测验之一的分数 |
| 外向性 | AMCAT人格测验之一的分数 |
| 营养疗法 | AMCAT人格测验之一的分数 |
| 开放性到经验 | 分数在AMCAT的个性测试的部分之一 |
二、数据预处理
- 目标变量:Salary(薪资)。
- 自变量(特征变量):除了Salary之外的其他变量。
import pandas as pd
import numpy as np
data=pd.read_csv('B题附件.csv')
data.info()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 2998 entries, 0 to 2997
Data columns (total 34 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 ID 2998 non-null int64
1 Gender 2998 non-null object
2 DOB 2998 non-null object
3 10percentage 2998 non-null float64
4 10board 2998 non-null object
5 12graduation 2998 non-null int64
6 12percentage 2998 non-null float64
7 12board 2998 non-null object
8 CollegeID 2998 non-null int64
9 CollegeTier 2998 non-null int64
10 Degree 2998 non-null object
11 Specialization 2998 non-null object
12 collegeGPA 2998 non-null float64
13 CollegeCityID 2998 non-null int64
14 CollegeCityTier 2998 non-null int64
15 CollegeState 2998 non-null object
16 GraduationYear 2998 non-null int64
17 English 2998 non-null int64
18 Logical 2998 non-null int64
19 Quant 2998 non-null int64
20 Domain 2998 non-null float64
21 ComputerProgramming 2998 non-null int64
22 ElectronicsAndSemicon 2998 non-null int64
23 ComputerScience 2998 non-null int64
24 MechanicalEngg 2998 non-null int64
25 ElectricalEngg 2998 non-null int64
26 TelecomEngg 2998 non-null int64
27 CivilEngg 2998 non-null int64
28 conscientiousness 2998 non-null float64
29 agreeableness 2998 non-null float64
30 extraversion 2998 non-null float64
31 nueroticism 2998 non-null float64
32 openess_to_experience 2998 non-null float64
33 Salary 2998 non-null int64
dtypes: float64(9), int64(18), object(7)
memory usage: 796.5+ KB
描述性统计:可以看到每一列数据的数量,均值,最大最小值等信息
查看是否有缺失值:
data.isnull().sum()
根据皮尔逊相关性绘制热力图
# seaborn中文乱码解决方案
from matplotlib.font_manager import FontProperties
myfont=FontProperties(fname=r'C:\Windows\Fonts\simhei.ttf',size=40)
sns.set(font=myfont.get_name(), color_codes=True)
data_corr = data.corr(method="spearman")#计算相关性系数
plt.figure(figsize=(20,15))#figsize可以规定热力图大小
fig=sns.heatmap(data_corr,annot=True,fmt='.2g')#annot为热力图上显示数据;fmt='.2g'为数据保留两位有效数字
fig
fig.get_figure().savefig('data_corr.png')#保留图片
下图当中,可以判断各个特征之间是否有影响,如果系数越大,则变量之间相关性越强。

计算每个学生到现在为止的年龄:
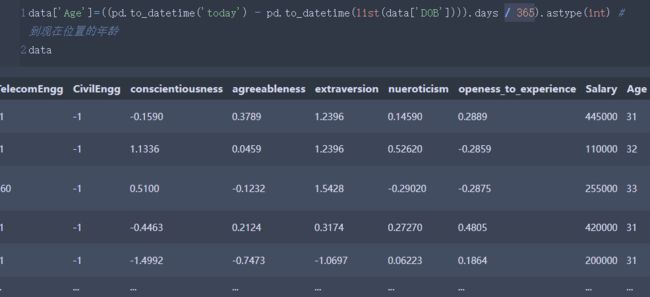
data['Age']=((pd.to_datetime('today') - pd.to_datetime(list(data['DOB']))).days / 365).astype(int) # 到现在位置的年龄
data
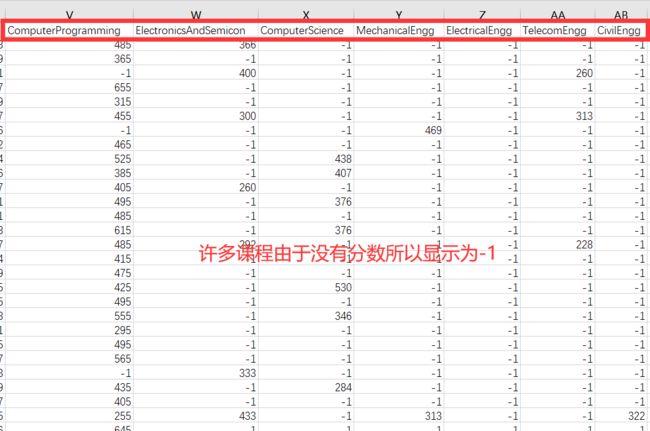
观察数据发现,在AMCAT的某些课程当中,由于许多同学没有分数,因此分数显示的是-1,所以为了进行更好的预测,在数据清理的时候将 -1 替换为总课程的平均值,以获得更好的预测。
columns = ['ComputerProgramming','ElectronicsAndSemicon','ComputerScience','MechanicalEngg','ElectricalEngg','TelecomEngg','CivilEngg']
for col in columns:
data[col] = data[col].replace({ -1 : np.nan})#先将-1填充为空值
data[col] = data[col].fillna(data[col].mean()) #再将空值替换为平均值
同时,将性别这列数字化:
data['Gender'] = data['Gender'].replace({'m': 0, 'f': 1})
data
将以数字开头的属性类更改名字:
data.rename(columns ={'10percentage':'tenth_percentage','12percentage':'twelveth_percentage','10board':'tenth_board','12graduation':'twelveth_graduation','12board':'twelveth_board',}, inplace =True)
data
data.to_csv('finish.csv')
三、第一问
分析影响高校工程类专业毕业生就业的主要因素。
根据前面的题目描述可知,我们需要使用薪水来作为就业情况的表示。
1、方法一:绘制图形
这里选择使用柱形图
plt.style.use('ggplot')
plt.bar(x.tenth_percentage,y,color ="red")
plt.xlabel("10th_percantage")#在10年级考试中获得的总成绩
plt.ylabel("salary")
plt.title("10th marks vs salary")
plt.bar(x.twelveth_percentage,y,color ="blue")
plt.xlabel("12th_percantage")#在12年级考试中获得的总成绩
plt.ylabel("salary")
plt.title("12th marks vs salary")
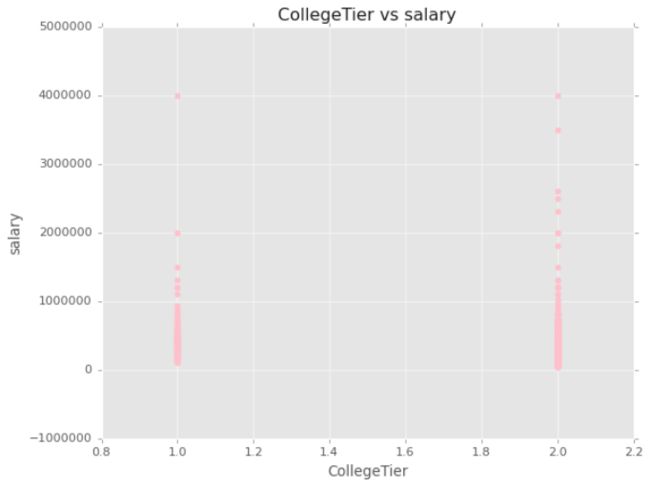
plt.scatter(x.CollegeTier,y,color ="pink")
plt.xlabel("CollegeTier")#学院所在城市的层
plt.ylabel("salary")
plt.title("CollegeTier vs salary")
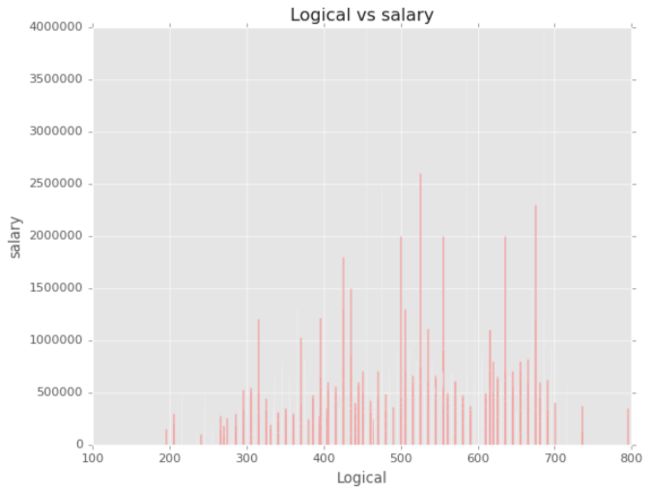
plt.bar(x.Logical,y,color ="red")
plt.xlabel("Logical")#逻辑能力
plt.ylabel("salary")
plt.title("Logical vs salary")
plt.bar(x.TelecomEngg,y,color ="black")
plt.xlabel("TelecomEngg")#电信工程得分
plt.ylabel("salary")
plt.title("TelecomEngg vs salary")
plt.bar(x.collegeGPA,y,color ="purple")
plt.xlabel("collegeGPA")#毕业时的GPA总计
plt.ylabel("salary")
plt.title("collegeGPA vs salary")
plt.figure(figsize = (15,8))
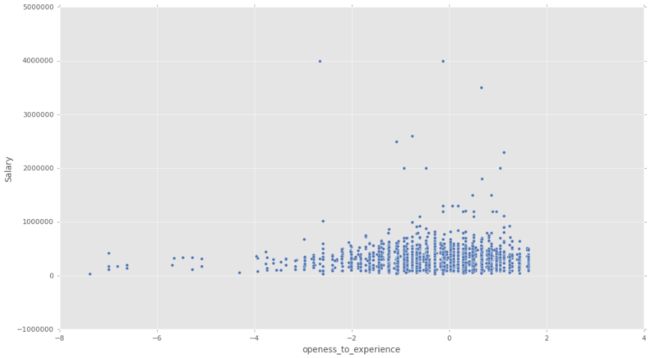
# 性格测试和薪水
sns.scatterplot(data.openess_to_experience, data.Salary, palette = 'inferno')
2、方法二:多元线性回归
由于多元线性回归的自变量需要是数值类型,考虑把Degree,Specialization,CollegeState变成数值。
preprocessing.OrdinalEncoder:特征专用,能够将分类特征转换为分类数值
# 由于多元线性回归的自变量需要是数值类型,考虑把Degree,Specialization,CollegeState变成数值。
# preprocessing.OrdinalEncoder:特征专用,能够将分类特征转换为分类数值
from sklearn.preprocessing import OrdinalEncoder
data_=data.copy()
data_
# 取出需要转换的两个字段
OrdinalEncoder().fit(data_[['Degree','Specialization','CollegeState']]).categories_
# 使用OrdinalEncoder将字符型变成数值
data_[['Degree','Specialization','CollegeState']]=OrdinalEncoder().fit_transform(data_[['Degree','Specialization','CollegeState']])
x = sm.add_constant(data_[['Gender', 'tenth_percentage',
'twelveth_graduation', 'twelveth_percentage',
'CollegeID', 'CollegeTier', 'Degree', 'Specialization', 'collegeGPA',
'CollegeCityID', 'CollegeCityTier', 'CollegeState', 'GraduationYear',
'English', 'Logical', 'Quant', 'Domain', 'ComputerProgramming',
'ElectronicsAndSemicon', 'ComputerScience', 'MechanicalEngg',
'ElectricalEngg', 'TelecomEngg', 'CivilEngg', 'conscientiousness',
'agreeableness', 'extraversion', 'nueroticism', 'openess_to_experience']]) #生成自变量
y = data['Salary'] #生成因变量
model = sm.OLS(y, x) #生成模型
result = model.fit() #模型拟合
result.summary() #模型描述
在这个结果中,我们主要看“coef”、“t”和“P>|t|”这三列。coef就是前面说过的回归系数,const这个值就是回归常数,所以我们得到的这个回归模型就是y = coef这列 × \times ×对应的系数。
而“t”和“P>|t|”这两列是等价的,使用时选择其中一个就行,其主要用来判断每个自变量和y的线性显著关系。从图中还可以看出,Prob (F-statistic)为1.40e-92,这个值就是我们常用的P值,其接近于零,说明我们的多元线性方程是显著的,也就是y与自变量有着显著的线性关系,而R-squared是0.161,也说明这个线性关系并不显著。
理论上,这个多元线性方程已经求出来了,但是效果一般,我们还是要进行更深一步的探讨。
前面说过,y与自变量有着显著的线性关系,这里要注意所有的自变量被看作是一个整体,y与这个整体有显著的线性关系,但不代表y与其中的每个自变量都有显著的线性关系,我们在这里要找出那些与y的线性关系不显著的自变量,然后把它们剔除,只留下关系显著的。
我们可以通过图中“P>|t|”这一列来判断,这一列中我们可以选定一个阈值,比如统计学常用的就是0.05、0.02或0.01,这里我们就用0.05,凡是P>|t|这列中数值大于0.05的自变量,我们都把它剔除掉,这些就是和y线性关系不显著的自变量,所以都舍去,请注意这里指的自变量不包括图中const这个值。
但是这里有一个原则,就是一次只能剔除一个,剔除的这个往往是P值最大的那个,比如图中P值最大的是GraduationYear,那么就把它剔除掉,然后再用剩下的自变量来重复上述建模过程,再找出P值最大的那个自变量,把它剔除,如此重复这个过程,直到所有P值都小于等于0.05,剩下的这些自变量就是我们需要的自变量,这些自变量和y的线性关系都比较显著,我们要用这些自变量来进行建模。
我们可以将上述过程写成一个函数,命名为looper,代码如下:
def looper(limit):
cols = ['Gender', 'tenth_percentage',
'twelveth_graduation', 'twelveth_percentage',
'CollegeID', 'CollegeTier', 'Degree', 'Specialization', 'collegeGPA',
'CollegeCityID', 'CollegeCityTier', 'CollegeState', 'GraduationYear',
'English', 'Logical', 'Quant', 'Domain', 'ComputerProgramming',
'ElectronicsAndSemicon', 'ComputerScience', 'MechanicalEngg',
'ElectricalEngg', 'TelecomEngg', 'CivilEngg', 'conscientiousness',
'agreeableness', 'extraversion', 'nueroticism', 'openess_to_experience']
for i in range(len(cols)):
data1 = data_[cols]
x = sm.add_constant(data1) #生成自变量
y = data_['Salary'] #生成因变量
model = sm.OLS(y, x) #生成模型
result = model.fit() #模型拟合
pvalues = result.pvalues #得到结果中所有P值
pvalues.drop('const',inplace=True) #把const取得
pmax = max(pvalues) #选出最大的P值
if pmax>limit:
ind = pvalues.idxmax() #找出最大P值的index
cols.remove(ind) #把这个index从cols中删除
else:
return result
result = looper(0.05)
result.summary()
由上图的相关系数可以看出,薪水和twelveth_graduation,twelveth_percentage,CollegeTier,Degree,English,ComputerProgramming具有较强的相关性。
3、方法三:多因素方差分析
多因素方差分析,用于研究一个因变量是否受到多个自变量(也称为因素)的影响,它检验多个因素取值水平的不同组合之间,因变量的均值之间是否存在显著的差异。多因素方差分析既可以分析单个因素的作用(主效应),也可以分析因素之间的交互作用(交互效应),还可以进行协方差分析,以及各个因素变量与协变量的交互作用。
根据观测变量(即因变量)的数目,可以把多因素方差分析分为:单变量多因素方差分析(也叫一元多因素方差分析)与多变量多因素方差分析(即多元多因素方差分析)。本案例是一元多因素方差分析。
这里使用SPSS进行演示:
1、首先在文件选项卡当中导入 finish.csv 数据:

2、分析-》 一般线性模型-》单变量


4、方法四:决策树
使用机器学习算法,可以转换成决策树来得到特征重要性排名:
from sklearn import tree
# 从sklearn中导入tree
from sklearn import datasets, model_selection
# 从sklearn中导入datasets用于加载数据集,这里我们使用iris数据集
# 从sklearn中导入model_selection用户划分测试集和训练集合
feature_name = ['Gender', 'tenth_percentage',
'twelveth_graduation', 'twelveth_percentage',
'CollegeID', 'CollegeTier', 'Degree', 'Specialization', 'collegeGPA',
'CollegeCityID', 'CollegeCityTier', 'CollegeState', 'GraduationYear',
'English', 'Logical', 'Quant', 'Domain', 'ComputerProgramming',
'ElectronicsAndSemicon', 'ComputerScience', 'MechanicalEngg',
'ElectricalEngg', 'TelecomEngg', 'CivilEngg', 'conscientiousness',
'agreeableness', 'extraversion', 'nueroticism', 'openess_to_experience','Age']
X = data_[feature_name]
Y = data_['Salary']
# 划分训练集和测试集 8:2
x_train,x_test, y_train, y_text = model_selection.train_test_split(X, Y, test_size=0.2, random_state=0)
# 创建一颗分类树,默认使用Gini
classification_tree = tree.DecisionTreeClassifier()
classification_tree.fit(x_train, y_train)
# 输出每个特征的重要性
[*zip(feature_name,classification_tree.feature_importances_)]
四、第二问
根据附件一建立模型,刻画工程类专业毕业生薪水和各因素的关系。
先画一下薪水分布:
plt.figure(figsize = (12, 6))
plt.subplot(121)
# 薪水分布
plt.title('Salary Distribuition')
sns.distplot(data['Salary'])
plt.subplot(122)
g1 = plt.scatter(range(data.shape[0]), np.sort(data.Salary.values))
# 薪水分布曲线
g1= plt.title("Salary Curve Distribuition", fontsize=15)
g1 = plt.xlabel("")
g1 = plt.ylabel("Salary", fontsize=12)
plt.subplots_adjust(wspace = 0.3, hspace = 0.5,
top = 0.9)
plt.show()
1、回归关系
这里说的是各个因素,那就要全部因素考虑进来,那就仿照第一问的方法二,可能需要把所有的object变量都变成int或者float类型,然后再进行拟合,得到具体的回归方程。
2、薪水预测
印度工科学生毕业后的工作情况和薪水。但是我们都不知道影响印度工程专业毕业生工资的不同因素是什么。该项目根据第 10 和第 12 班的分数百分比、大学等级、不同科目的分数、总体 gpa、逻辑推理和毕业年份等参数来预测工程师的薪水。该项目包括一个 ML 模型,该模型使用不同的算法来预测毕业生的薪水。这里我们使用一些主要因素来多薪水做预测(你也可以试试全部因素)。
from sklearn.preprocessing import LabelEncoder
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.linear_model import Ridge
from sklearn.linear_model import Lasso
from sklearn.linear_model import ElasticNet
from sklearn.neighbors import KNeighborsRegressor
from sklearn.svm import SVR, LinearSVR
from sklearn.tree import DecisionTreeRegressor
from sklearn.ensemble import RandomForestRegressor
from sklearn.ensemble import GradientBoostingRegressor
from sklearn.ensemble import AdaBoostRegressor
from sklearn.neural_network import MLPRegressor
def preprocess_inputs(data_):
data_ = data_.copy()
data_['Degree'] = LabelEncoder().fit_transform(data_.Degree)
data_['Specialization'] = LabelEncoder().fit_transform(data_.Specialization)
X=data_[['Gender', 'tenth_percentage',
'twelveth_graduation', 'twelveth_percentage',
'CollegeID', 'CollegeTier', 'Degree', 'Specialization', 'collegeGPA',
'CollegeCityID', 'CollegeCityTier', 'CollegeState', 'GraduationYear',
'English', 'Logical', 'Quant', 'Domain', 'ComputerProgramming',
'ElectronicsAndSemicon', 'ComputerScience', 'MechanicalEngg',
'ElectricalEngg', 'TelecomEngg', 'CivilEngg', 'conscientiousness',
'agreeableness', 'extraversion', 'nueroticism', 'openess_to_experience','Age']]
y=data_['Salary']
X_train, X_test, y_train, y_test = train_test_split(x, y, train_size=0.7, shuffle=True, random_state=43)
scaler = StandardScaler()
scaler.fit(X_train)
X_train = pd.DataFrame(scaler.transform(X_train), columns = X_train.columns, index = X_train.index)
X_test = pd.DataFrame(scaler.transform(X_test), columns = X_test.columns, index = X_test.index)
return X_train, X_test, y_train, y_test
X_train, X_test, y_train, y_test = preprocess_inputs(data_)
X_train
models = {
' Linear Regression': LinearRegression(),
' Ridge': Ridge(),
' Decision Tree': DecisionTreeRegressor(),
' Random Forest': RandomForestRegressor(random_state=100,
bootstrap=True,
max_depth=2,
max_features=2,
min_samples_leaf=3,
min_samples_split=5,
n_estimators=3),
' Lasso' : Lasso(),
' Elastic Net' : ElasticNet(),
' Neural network' : MLPRegressor(),
' Gradient Boosting': GradientBoostingRegressor(),
'Adaboost Classifier': AdaBoostRegressor(),
'KNN': KNeighborsRegressor()
}
for name, model in models.items():
model = model.fit(X_train, y_train)
print(name + " trained")
for name, model in models.items():
print(name,model.score(X_test, y_test))
emmmmmm,训练的结果最好的也才0.23,不是很理想
五、第三问
根据以上的分析,对我国高校工程类专业学生培养是否有一定的启迪?写一份建议书。
注意不要乱写,不是让你编个小论文,要根据前面两个问题进行分析,从而写关于我国的建议(注意:针对自己本校就行了)。最终目的是希望学生的就业薪水更高。
比如哪些因素不应该过度严厉,哪些因素学校应该严抓等。。。。应该有这方面论文,去找找。
参考:
1、对学校就业工作的建议
2、大学生就业形势
3、对学校人才培养工作有何建议