三元组损失tripletloss
雷郭出品
-
- 先验知识
- 1.Triplet loss
- 2. Hard Triplets选择
先验知识
题外话(来自网络):
(最近,learning to rank 的思想逐渐被应用到很多领域,比如google用来做人脸识别(faceNet),微软Jingdong Wang 用来做 person-reid 等等。learning to rank中其中重要的一个步骤就是找到一个好的similarity function,而triplet loss是用的非常广泛的一种。)
为什么要提出三元组损失?
三元组损失(Triplet loss)函数是当前应用较为广泛的一种损失函数,最早由Google研究团队在论文《FaceNet:A Unified Embedding for Face Recognition》所提出,常用在人脸识别任务中。目的是做到非同类极相似样本的区分,比如说对兄弟二人的区分。
所以,Triplet loss的优势在于细节区分,即当两个输入相似时,Triplet loss能够更好地对细节进行建模,相当于加入了两个输入差异性差异的度量,学习到输入的更好表示。
优点:
基于Triplet loss的神经网络模型可以很好的对细节进行区分,尤其是在图像分类任务中,当两个输入很相似的时候,Triplet loss对这两个差异性较小的输入向量可以学习到更好的表示,从而在分类任务中表现出色。
相比其他分类损失函数,Triplet loss通常能在训练中学习到更好的细微的特征feature,更特别的是Triplet loss能够根据模型训练的需要设定一定的阈值。
带Triplet loss的网络结构在进行训练的时候一般都会设置一个阈值margin,设计者可以通过改变margin的值来控制正负样本的距离。
缺点:
虽然Triplet loss很有效,但也有缺点:三元组的选取导致数据的分布并不一定均匀,所以在模型训练过程表现很不稳定,而且收敛慢,需要根据结果不断调节参数,而且Triplet loss比分类损失更容易过拟合。
所以,大多数情况下,我们会把这种方法放在模型的预训练过程中,或者和softmax函数(分类损失)结合在一起使用。
对于输入x,经过网络A后得到f(x)
相当于从特征x映射到特征空间R1
在R1中,我们可以比较两个特征向量f(x1)和f(x2)之间的距离
我们希望的是同一个类别的输入得到的特征向量之间的距离是较小的
而不同类别的输入得到的特征向量之间的距离是较大的
有了这个先验思想之后再提出三元组的概念
1.Triplet loss
看到这张图
首先要知道A,N,P分别代表的是什么
这三个就组成了三元组中的三元
三元组的构成:
首先从训练数据集中随机选一个样本,该样本称为Anchor,记为x_a
然后再同时随机选取一个和Anchor属于同一类的样本和一个与Anchor不同类的样本
两个样本分别称为Positive (记为x_p)和Negative (记为x_n)
由此构成一个(Anchor,Positive,Negative)三元组。
由先验知识可知
这里的A,P,N是输入x
所以经过某个网络之后得到各自的特征映射
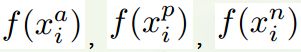
下缀i表示第i个batch(总不能是第i个样本吧,一个样本只能是三元中的一个啊),f表示网络等效的函数,上缀a,p,n表示对应的三元
我们希望:

由上图可知
对于任意的batch,我们都希望选定的样本组合都能满足上述的不等式
由此我们的损失函数就可以写成如下的形式
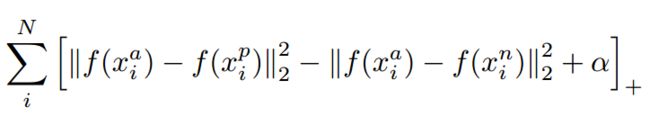
当中括号中的式子的值大于等于零时,取了+号之后是本身,此时loss大于零,会更新参数;
当中括号中的式子的值小于零时,取了+号之后是零,这时就没办法产生梯度,也就无法更新参数,
其实这是符合逻辑的,因为当式子的值小于零时,说明已经达到了目的,也就需要再更新了。
注意,如果训练完后样本中的三元组都能满足这样的情况自然是好的,但是如果在训练的过程中碰到这样的样本是我们不想要的,因为这样的样本对于网络训练来说毫无作用!!后面有介绍。
我们希望上面的值越小越好,即min(loss);
由于组成的三项的相对大小不一定,所以需要讨论;
这里距离用欧式距离度量,+表示[]内的值大于零的时候,取该值为损失,小于零的时候,损失为零。
这里设第一项为A1;第二项为A2;第三项为A3(A3始终是大于零的吧,对应magin)
则
- 当A1+A3
- 当A1+A3>A2 && A1
- 当A1>A2时,整体值为正数,则最终取值为正,损失相对较大,可以学习;
- 当A1+A3>A2 && A1
由上面的分析可知
-
Easy Triplets:
我们不希望碰到Situation1,这样没法学习(或者学习很慢(毕竟样本有很多,可以抵消))
网上也称此时positive pair 的距离远远小于negative pair的距离。即,类内距离很小,类间很大距离,这种情况不需要优化。我觉得这种说法不对,因为我觉得在训练的时候碰到这种情况肯定是有的(毕竟样本是随机选择的),但我们希望尽量不要碰到这种情况,因为这样很浪费时间 -
Semi Hard Triplets:
situation2虽然整体值为正数,但是值比较小,整体值小于A3(margin),术语也叫在一个margin内,能优化,但是还是相对situation3来说慢 -
Hard Triplets
当碰到situation3时
对应的就是下面这种情况
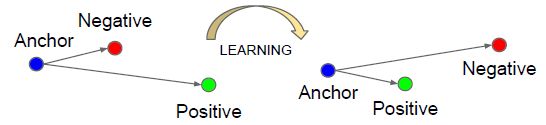
此时AP之间的距离比AN之间的距离都要大
说明此时跟理想情况相差甚远,因此有更大的动力来进行学习
我们在训练的时候会人为地去选择这种Hard Triplets
这样训练起来更快啊
(然而SSDG中并没有使用hardTriplet)
对于阈值margin的设置需要注意选择合适大小的值,理论上来说,较大的margin能够增强模型对不同类样本的区分度,但是如果在训练初期就将margin设置得比较大,则可能会增加模型训练的难度,进而出现网络不收敛的情况。在模型训练初期先使用一个较小的值对网络进行初始化训练,之后再根据测试的结果对margin的值进行适当的增大或缩小,这样可以在保证网络收敛的同时让模型也能拥有一个较好的性能。(但是实际好像一般都是用一个固定的margin)
我的理解就是要慢慢来,不能一蹴而就。
损失函数的目的就是希望a和p之间的距离越近,a和n之间的距离越远,两者距离差值为margin(人为可控)
如果margin一开始就很大,我的理解是loss就很大,从而梯度就很大,可能会出现震荡的情况,即没法慢慢的拉开两者之间的距离。我暂时只能这么理解。
下面就介绍如何去选择Hard Triplets
选择之前先看看损失函数的导数(绝对值的平方就相当于没有绝对值的平方)
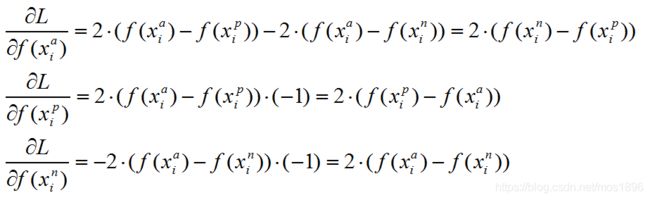
可以看到后两者的导数值就是损失函数的组成成分(网上说是一个训练时的小trick)
原话:可以看到,对x_p和x_n特征表达的梯度刚好利用了求损失时候的中间结果,给的启示就是,如果在CNN中实现 triplet loss layer, 如果能够在前向传播中存储着两个中间结果,反向传播的时候就能避免重复计算。这仅仅是算法实现时候的一个Trick。
2. Hard Triplets选择
我看了很多人的博客,
但是我感觉理解了原理之后感觉很多代码都在一个地方有问题,
即mask处,
mask的作用是筛选出与anchor同一类的样本(positive)或者不同类(negative)的样本
话不多说,直接看代码。
首先对于一个batchsize中的样本,每一个样本都可以找到其对应的同类距离最大,异类距离最小的样本
从而形成每一个样本对应的三元组(即当前样本为anchor,与之距离最大同类样本为positive,距离最小异类样本为negative)。
所以说在选择Hard Triplets时,会产生batchsize个三元组,即每一个元素都会作为一个anchor产生一组独一无二的三元组(前提是每个类别的数目至少要为2)。
首先要定义一个可以计算各个样本之间的距离的函数
假设bachsize为m
每个样本的维度为n
则距离矩阵的形状应该是m x m
其中主对角线的数值为0,因为自己离自己肯定是零距离
同时该距离矩阵也得是对称矩阵
举个例子:
假设bathsize为3,每个样本的维度为2
则距离矩阵应该是如下3 x 3的对称矩阵:
比如某个batch为:
a b
c d
e f
则距离矩阵应该是:
| 0 | (a-c)^2 + (b-d)^2 | (a-e)^2+ (b-f)^2 |
|---|---|---|
| (a-c)^2 + (b-d)^2 | 0 | (c-e)^2+ (d-f)^2 |
| (a-e)^2+ (b-f)^2 | (c-e)^2+ (d-f)^2 | 0 |
其他batchsize和特征维度可以类比上表
那怎么写出这样的程序呢?
看如下的代码:
class TripletLoss(nn.Module):
def __init__(self, margin=0.3):
super(TripletLoss, self).__init__()
self.margin = margin
self.ranking_loss = nn.MarginRankingLoss(margin=margin) # 获得一个简单的距离triplet函数
def forward(self, inputs, labels):
n = inputs.size(0) # 获取batch_size,这里的inputs就是输入矩阵,即batchsize * 特征维度
# Compute pairwise distance, replace by the official when merged
dist = torch.pow(inputs, 2).sum(dim=1, keepdim=True).expand(n, n) # 每个数平方后, 进行加和(通过keepdim保持2维),再扩展成nxn维
dist = dist + dist.t() # 这样每个dis[i][j]代表的是第i个特征与第j个特征的平方的和
dist.addmm_(1, -2, inputs, inputs.t()) # 然后减去2倍的 第i个特征*第j个特征 从而通过完全平方式得到 (a-b)^2
dist = dist.clamp(min=1e-12).sqrt() # 然后开方
# For each anchor, find the hardest positive and negative
mask = labels.expand(n, n).eq(labels.expand(n, n).t()) # 这里mask[i][j] = 1代表i和j的label相同, =0代表i和j的label不相同
dist_ap, dist_an = [], []
for i in range(n):
dist_ap.append(dist[i][mask[i]].max().unsqueeze(0)) # 在i与所有有相同label的j的距离中找一个最大的
dist_an.append(dist[i][mask[i] == 0].min().unsqueeze(0)) # 在i与所有不同label的j的距离找一个最小的
dist_ap = torch.cat(dist_ap) # 将list里的tensor拼接成新的tensor
dist_an = torch.cat(dist_an)
# Compute ranking hinge loss
y = torch.ones_like(dist_an) # 声明一个与dist_an相同shape的全1tensor
loss = self.ranking_loss(dist_an, dist_ap, y)
return loss
nn.MarginRankingLoss()
TripletMarginLoss
torch.cat()
max(),eq()
eq(),lt(),ne()
torch.clamp
torch.squeeze(),unsqueeze()
torch.expand
torch.expand
torch.expand
torch.sum
torch.mean,rand(),pow()
torch.t()
torch.addmm()
参考网址1
参考网址2
- 代码中的:
n = inputs.size(0) # 获取batch_size,这里的inputs就是输入矩阵,即batchsize * 特征维度
# Compute pairwise distance, replace by the official when merged
dist = torch.pow(inputs, 2).sum(dim=1, keepdim=True).expand(n, n) # 每个数平方后, 进行加和(通过keepdim保持2维),再扩展成nxn维
dist = dist + dist.t() # 这样每个dis[i][j]代表的是第i个特征与第j个特征的平方的和
dist.addmm_(1, -2, inputs, inputs.t()) # 然后减去2倍的 第i个特征*第j个特征 从而通过完全平方式得到 (a-b)^2
dist = dist.clamp(min=1e-12).sqrt() # 然后开方
起到的作用是求出单个batch中的每个样本跟其他样本的欧式距离
得到的矩阵是batchsize * batchsize
同时是一个对称矩阵(因为样本1到样本3的距离等于样本3到样本1的距离)
同时主对角线的数值为零(因为样本1到样本1的距离肯定是零)
- 代码中的:
for i in range(n):
dist_ap.append(dist[i][mask[i]].max().unsqueeze(0)) # 在i与所有有相同label的j的距离中找一个最大的
dist_an.append(dist[i][mask[i] == 0].min().unsqueeze(0)) # 在i与所有不同label的j的距离找一个最小的
我认为是错误的,因为dist和mask同样都是batchsize * batchsize的形状
这里dist的第二个索引用的是一个tensor
没见过这种操作
我实际测试了一下:
a8=torch.from_numpy(np.array([[0,20,30],[20,0,40],[30,40,0]]))
a9=a8[0][[1,0,1]]
print(“a9”,a9)
a9 tensor([20, 0, 20], dtype=torch.int32)
可以发现根本就没有起到mask掩膜的作用
而是有点像transpose函数的转换维度位置的作用
我一开始改成了下面这种:
for r i in range(n):
dist_ap.append((dist[i]*mask[i]).max().unsqueeze(0)) # 在i与所有有相同label的j的距离中找一个最大的
dist_an.append((dist[i]*(mask[i] == 0)).min().unsqueeze(0)) # 在i与所有不同label的j的距离找一个最小的,这里出了点问题(要考虑把0先剃掉在来求min,因为0本就是min)
第一个求max没有问题
第二个求min就出现了问题,因为0的存在会影响min的判断
比如明明不同类的最小值是一个非零的正数,但是由于相乘之后0的存在,硬是把0当成了最小值
所以我觉得要先剔除元素
我把第二个改成这样的:
temp=[]
temp=dist[i]+mask[i] #我现在就是担心这些奇葩的操作可能pytorch不支持其反向传播
temp1=[]
for j in range(len(dist[i])):
if temp[j]==dist[i][j]: #筛选出mask中的0对应的dist中的元素
temp1.append(dist[i][j])
temp2=torch.tensor(temp1)
dist_an.append(temp2.min().unsqueeze(0))
现在的疑惑就是我弄这么多的列表和tensor操作,pytorch支不支持反向传播??
- 官网MarginRankingloss
Creates a criterion that measures the loss given inputs x1 ,x2 , two 1D mini-batch Tensors, and a label 1D mini-batch tensor y (containing 1 or -1).
本意是两个输入x1和x2是一维,即只有一个【】
如[1,2,3]
loss = nn.MarginRankingLoss()
input1 = torch.randn(3, requires_grad=True)
input2 = torch.randn(3, requires_grad=True)
target = torch.randn(3).sign()
output = loss(input1, input2, target)
output.backward()
这里的input1打印出来就是:
input1: tensor([ 0.3719, -0.3349, -0.3026], requires_grad=True)
这里reduction默认是Mean,所以得到的output是一个标量,即取了平均值后的值
如果reduction设定了是none,则得到的output是一个跟input1相同shape的tensor
还有一个要注意的点:最后的结果中不会有负数,因为max操作会将0作为兜底。
这个函数的作用就是假设你已经找到了
achor,positive,negative,
并且把两两之间的distance算出来了(如a和p之间,a和n之间)
然后就可以带入这个函数进行计算
对应的就是如下的公式:
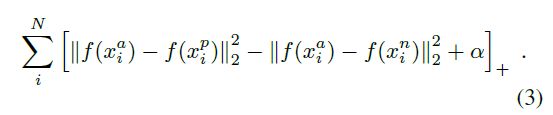
![]()
上面的两个式子可以一一对应
如x1对应第一张中的第二项
max对应第一张中的下标+
alpha对应margin
y是1或者-1,比较灵活,这里为了跟x1的描述一致,则y需要取1
先分析这些,之后再添
同一天我就发现了是我的理解出现了错误
详情看一下下面的代码:
A=torch.arange(12).reshape(1,3,4)
print("A:",A)
print("A>5:",A>5)
B=A[A>5]
print("A[A>5]:",A[A>5])
A: tensor([[[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]]])
A>5: tensor([[[False, False, False, False],
[False, False, True, True],
[ True, True, True, True]]])
A[A>5]: tensor([ 6, 7, 8, 9, 10, 11])
确实是可以这样进行筛选
再来看一个代码:
a8=torch.from_numpy(np.array([[0,20,30],[20,0,40],[30,40,0]]))
a9=a8[0][[True,False,True]]
print("a9:",a9)
a9: tensor([ 0, 30], dtype=torch.int32)
但是这样就不行
a8=torch.from_numpy(np.array([[0,20,30],[20,0,40],[30,40,0]]))
a9=a8[0][[1,0,1]] #pytorch的筛选机制,非得是bool形式,不能是0,1的形式
print("a9:",a9)
a9: tensor([20, 0, 20], dtype=torch.int32)
我猜测: pytorch的筛选机制,非得是bool形式,不能是0,1的形式
同理如下可以:
a2=torch.from_numpy(np.array([[0.0,20.0,30.0],[20.0,0.0,40.0],[30.0,40.0,0]]))
a3=torch.from_numpy(np.array([[True,False,True],[False,True,False],[True,False,False]]))
print("a2:",a2)
print("a3:",a3)
a4=a2[0][a3[0]]
print("a4",a4)
a2: tensor([[ 0., 20., 30.],
[20., 0., 40.],
[30., 40., 0.]], dtype=torch.float64)
a3: tensor([[ True, False, True],
[False, True, False],
[ True, False, False]])
a4 tensor([ 0., 30.], dtype=torch.float64)
而这样就不行:
a2=torch.from_numpy(np.array([[0.0,20.0,30.0],[20.0,0.0,40.0],[30.0,40.0,0]]))
a3=torch.from_numpy(np.array([[1,0,1],[0,1,0],[1,0,1]]))
print("a2:",a2)
print("a3:",a3)
a4=a2[0][a3[0]]
print("a4",a4)
a2: tensor([[ 0., 20., 30.],
[20., 0., 40.],
[30., 40., 0.]], dtype=torch.float64)
a3: tensor([[1, 0, 1],
[0, 1, 0],
[1, 0, 1]], dtype=torch.int32)
Traceback (most recent call last):
File "C:/Users/14215/PycharmProjects/untitled2/PytorchGrammar/test1.py", line 37, in <module>
a4=a2[0][a3[0]]
IndexError: tensors used as indices must be long, byte or bool tensors
我之前考虑long去了,没有考虑bool,结果就方向完全错了
总结:网上的代码没有毛病!我自己弄错了。
我自己犯错的原因在于惯性思维
因为我在很多地方看到True和1,False和0是等效的
然而在这里就不行
2022:05:11:
不使用hardTriplet的情况:
n个样本,算出nxn的距离矩阵,
对于每个样本anchor,有n种positive,n种negative,
也就是总共的三元组有n的三次方个,
求出每个对应的三元组损失,
最后只选择大于零的损失进行累加和,并且计算平均损失的时候分母是三元组损失大于零的组合总数。
具体代码参考SSDG中的代码。