【数学建模】 插值算法
插值算法在数学建模中是一个非常重要的算法,通常用来对已知的函数点进行数据、模型的处理和分析,而有时候现有的数据是极少的,不足以支撑分析的进行,这时就需要利用插值算法来“模拟产生”一些新的但又比较靠谱的值来满足需求,这就是插值的作用。
下面我来介绍数学建模比赛中常用的插值算法:拉格朗日插值法、牛顿插值法、Hermite插值、三次样条插值等。
1. 拉格朗日插值法
一般地,若已知y = f(x),在互不相同 n+1 个点X1,X2,...,Xn处的函数值y0,y1,y2...,yn,则可以考虑n+1个点的、次数不超过n的多项式y = Pn(x),使其满足:
要估计任一点ξ,ξ≠xi,i=0,1,2,...,n,则可以用Pn(ξ)的值作为准确值f(ξ)的近似值,此方法叫做“插值法”。
称式(*)为插值条件(准则),含xi(i=0,1,...,n)的最小区间[a,b],其中a=min{x0,x1,...,xn},b=max{x0,x1,...,xn}。
定理
满足插值条件的、次数不超过n的多项式是存在而且是唯一的。
构造拉格朗日插值多项式:
要构造拉格朗日插值多项式,那么需要先知道什么是拉格朗日插值多项式;
存在n个点:(x0,y0),(x1,y1),(x2,y2),...,(xn,yn),存在一个函数f(x)经过这n个点,那么此时这个函数f(x)就称为拉格朗日插值多项式。
下面通过举例来简述构造方法:
1. 两个点:(x0,y0),(x1,y1)构造一个函数f(x)经过这2个点。
不难发现,函数f(x)经过这2个点。
2. 三个点:(x0,y0),(x1,y1),(x2,y2)构造一个函数f(x)经过这3个点。
![]()
![]()
Ln(x)为拉格朗日插值多项式。
以上公式中x后面的0,1,2,...,k,i,...,n,n+1全部都是下标。
2. 牛顿插值法
差商的定义:
牛顿插值法公式:
很明显,与拉格朗日插值法相比,牛顿插值法的计算具有继承性,也就是说在计算x3处的插值时,不会牵扯到x3后面数值的运算,只会应用到前面数值的运算。
这两种插值法都存在龙格现象,也就是在图形的两端处会波动增大,产生明显的震荡。
因此这两种插值法应用不多。
3. Hermite插值
原理:
相关定理:
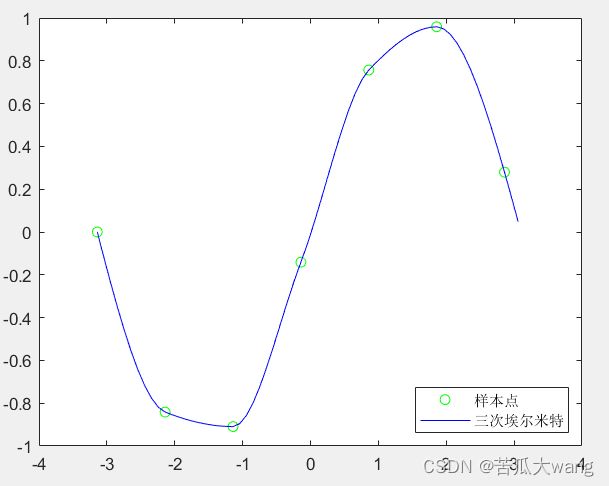
实际上直接使用Hermite插值得到的多项式次数较高,也存在这龙格现象,因此在实际应用中经常使用三次Hermite插值多项式。
matlab代码的实现结果:
使用pchip函数可实现
4. 三次样条插值
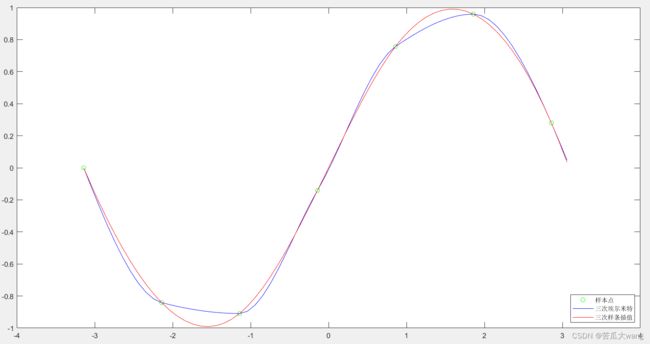
matlab代码实现结果:
使用spline函数可实现
由结果可以看出,三次样条插值算法的曲线比Hermite插值算法所得到的曲线更为平滑。在实际应用中这两种插值算法都具有好的应用性。
如果对数学建模算法感兴趣的朋友,可以通过该链接(https://b23.tv/av20238704/p1 )去找资料学习数学建模相关算法。
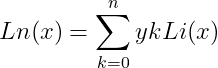
![f[x0,xk]=\frac{f(xk)-f(x0)}{xk-x0}](http://img.e-com-net.com/image/info8/0bc015bb21524d00bce302984db63756.gif)
![f[x0,x1,x2]=\frac{f[x1,x2])-f[x0,x1])}{x2-x0}](http://img.e-com-net.com/image/info8/9c1a5c7eeb76461f92bc638f181f7c50.gif)
![f[x0,x1,...,xk]=\frac{f[x1,x2,...,xk])-f[x0,x1,...,x(k-1)])}{xk-x0}](http://img.e-com-net.com/image/info8/d9d74e5b0a3a40a6a0bb96258edd7e6b.gif)
+f[x0,x1,x2](x-x0)(x-x1)+...+f[x0,x1,...,xn](x-x0)(x-x1)...(x-x(n-1))](http://img.e-com-net.com/image/info8/97881bc247964d699bb29ce2d207518e.gif)