数学建模：插值算法

插值算法

0.拉格朗日+牛顿插值问题

• 出现龙格现象（Runge）：在两端的数据远远偏离原函数规律**（产生类似过拟合的现象）**

• 仅保证值相等，未保证函数导数值相等，不可准确反映函数变化的趋势

• 解决方法：分段插值+埃尔米特&样条插值

1.分段三次埃尔米特插值+分段三次样条插值

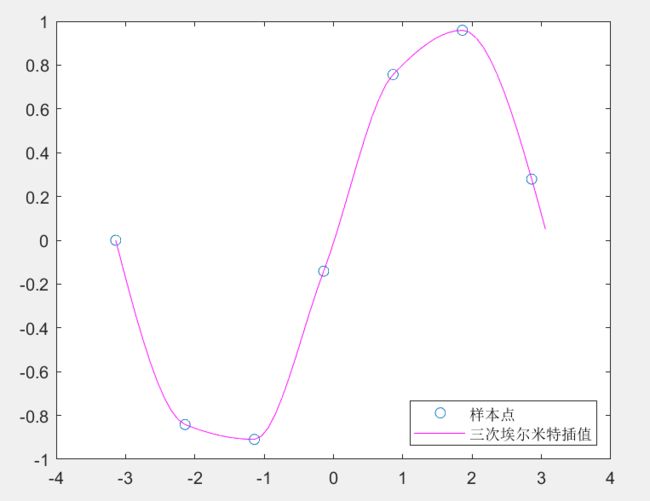
• 埃尔米特插值：保证值相等+一阶导数相等（更好反映变化趋势）

clear,clc;
%创建原(新)样本点
x = -pi : pi;
y = sin(x);
new_x = -pi : 0.1 : pi;

%三次埃尔米特插值（保证值和一阶导数都相等）
p1 = pchip(x,y,new_x); 

%作图plot函数
figure(1);
plot(x,y,"o",new_x,p1,"m-")
legend("样本点","三次埃尔米特插值","location","southeast");

• 效果图：

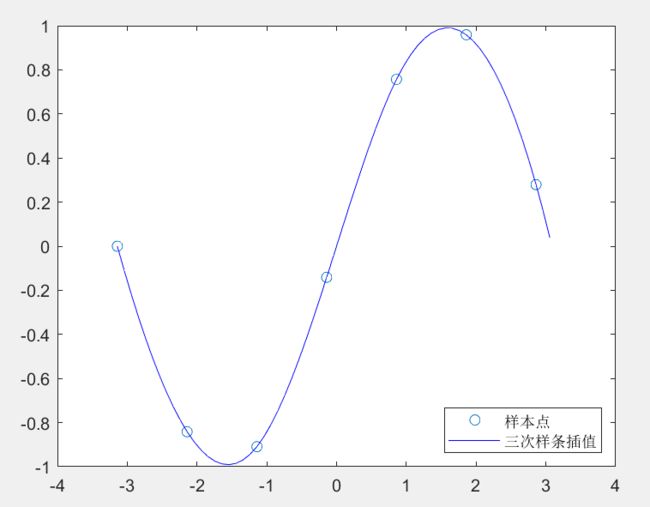
• 三次样条插值：二阶连续可微+区间内为三次多项式（更加光滑）

clear,clc;
%创建原(新)样本点
x = -pi : pi;
y = sin(x);
new_x = -pi : 0.1 : pi;

%三次样条插值（保证值、一阶导数相等，且二阶连续可微）
p2 = spline(x,y,new_x); 
figure(2);
plot(x,y,"o",new_x,p2,"b-")
legend("样本点","三次样条插值","location","southeast");

• 效果图：

2.实操练习

①题目：利用插值算法将偶数周的数据补全，并画出图线

②使用的函数+方法

# 直接从Excel赋值创建矩阵
# 使用size()函数获取矩阵的大小(1为获取行数，2为获取列数)
# 创建字符串数组(直接创建)
# 创建0矩阵zeros()
# 三次样条插值spline，三次埃尔米特插值pchip()
# 画图plot():颜色，点型，线型，线宽(linewidth)
# 画子图subplot(m,n,p)
# 设置xy坐标名称：xlabel，ylabel
# 设置图的标题:title()

③代码：

clc;
week = [1,3,5,7,9,11,13,15];
name = ["轮虫(10^6/L)","溶氧(mg/l)","COD(mg/l)","水温(℃)","PH值","盐度","透明度(cm)","总碱度","氯离子","透明度","生物量"];
%y矩阵直接用从Excel复制创建

result_spline = zeros(size(sample,1),15); %用于接收使用样条插值之后的全部结果
result_pchip = zeros(size(sample,1),15);
new_week = 1 : 15;

%遍历全部指标，利用三次样条插值进行计算
for row = 1 : size(sample , 1)
    row_sample = sample(row , :);
    result_spline( row , : ) = spline( week , row_sample , new_week);
    result_pchip( row , : ) = pchip( week , row_sample , new_week);
end

%利用subplot(m,n,p)函数进行多图绘制

for row1 = 1 : size(result , 1)
   subplot(3,4,row1)
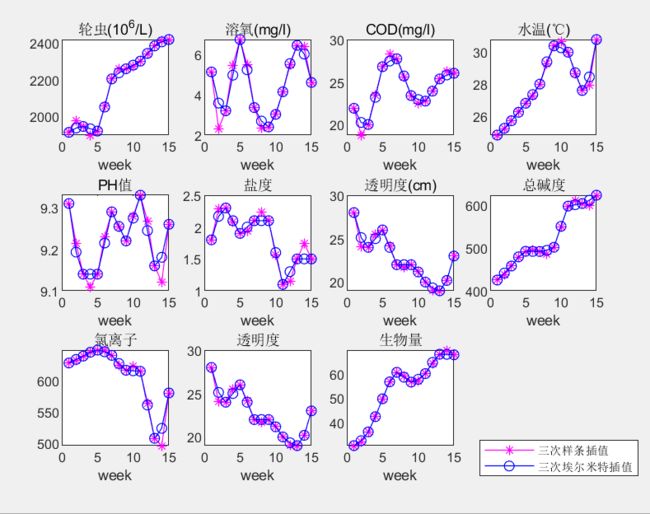
   plot(new_week,result_spline(row1 , :),"m*-",new_week,result_pchip(row1 , :),"bo-","linewidth",0.6);
   xlabel("week");
   title(name(row1));
end
legend("三次样条插值","三次埃尔米特插值","location","southeast");
%m 表示 p 个图排成 m 行，n 表示图排成 n 列，即整个figure中共有m * n张小图
%p 表示图所在的位置，p=1表示从左到右从上到下的第一个位置。

• 运行结果：