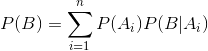paddle深度学习基础之损失函数
paddle深度学习基础之损失函数
前言
文章目录
- paddle深度学习基础之损失函数
-
- 前言
- 网络结构
- 损失函数
-
- 一、损失函数漫谈
- 二、交叉熵损失函数
-
-
- 1. Softmax函数
- 2.最大似然估计
- 3.贝叶斯公式
- 4.交叉熵损失函数
-
- 三、代码中的应用
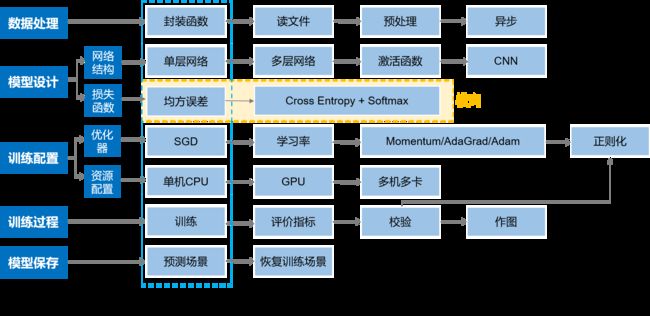
上一节，咱们通过优化网络结构，极大的提升了模型的精准度。本节，咱们将在损失函数上面做些文章。
网络结构
损失函数
一、损失函数漫谈
还记得我们之前做的房价预测模型，使用的损失函数是均方差损失函数。这对于房价预测模型这种需要模型不断接近真实房价，是比较合适的。但是对于分类模型，我们所预测的值是离散。举个例子，一张动物图片，我们来预测是猫、狗、牛。我们会假定，输出结果为0的是猫，输出结果为1的是狗，输出结果为2的是牛。如果我们使用均方差损失函数，预测值和真实值相减，并不具备物理意义。所以，分类模型使用均方差损失函数是不合适的。那么，接下来会介绍一种损失函数，能够很好的用于分类模型中。
二、交叉熵损失函数
1. Softmax函数
在介绍交叉熵损失函数之前，我们需要引入Softmax函数。这个函数经常作为分类模型的激活函数，用于将模型输出的各个标签的值进行转化，转化为总和为1的概率值，公式如下：
s o f t m a x ( x i ) = e x i ∑ j = 0 N e j x , i = 0 , . . . , C − 1 softmax(x_i) = \frac {e^{x_i}}{\sum_{j=0}^N{e^x_j}}, i=0, ..., C-1 softmax(xi)=∑j=0Nejxexi,i=0,...,C−1
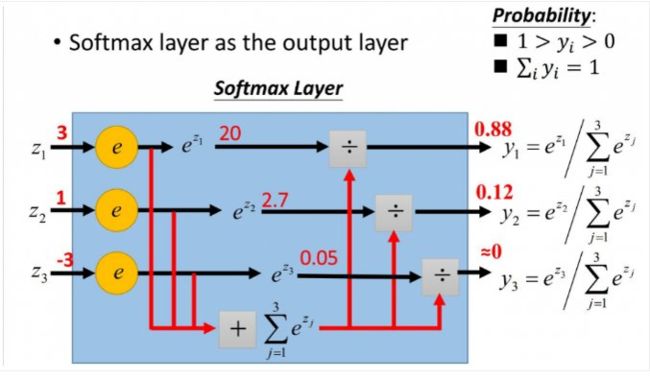
下面咱们看这个图，还是咱们前面说的猫狗牛三分类，最后全连接层输出的三个值是3、1、-3，接下来将进行如下转化：
从图中最后结果我们可以看出，将全连接层输出的结果，转化为了概率值，且相加之和为1.这就很符合我们的认知。我们希望模型在预测类型的时候，能够给出一个概率，而不是一个正常的数。
2.最大似然估计
什么叫最大似然估计呢，最合适的解释为：根据已知结果，反推最有可能造成这个结果的参数值。这是一种根据结果反推参数值的一种概率论方法。
这里我们可以对比着我们所学的一元二次曲线方程，我们通常会求它的极值。曲线方程可以类比为已知结果，我们所求的极值点就是造成这个结果的参数值。
这里我们可以对比着我们所学的一元二次曲线方程，我们通常会求它的极值。曲线方程可以类比为已知结果，我们所求的极值点就是造成这个结果的参数值。
下面这里篇博客讲的特别好，大家可以去看一下：
- 极大似然估计详解，写的太好了！
- 极大似然估计思想的最简单解释
3.贝叶斯公式
贝叶斯公式是我们概率论里比较重要的公式之一，它通常和全概率公式一起使用。
我们首先看一下全概率公式：
这个挺好理解的。举个简单的例子，你们班上一共有30名同学，其中20名为男生，10名为女生，男生中有10名同学在全年级排名前100名内，女生有8名同学在全年级排名前100名内。
我们需要计算你们班学生在全年级排名前100名的概率。
P(B)为全年级排名前100的学生的概率
P(A1) 为班级里男生的概率 ，P(A2)为班级里是女生的概率
P(B|A1)表示男生中在全年级排名前100名的概率
P(B|A2)表示女生中在全年级排名前100名的概率
P(B) = (20/30) x(10/20)+(10/30)x(8/10)=0.6
从上面的例子中，我们也能看出，是我们已知导致结果的原因，求最终结果概率，这也叫先验概率。
下面我们介绍的贝叶斯公式，称之为后验概率。已知结果，去推出各个原因的概率；通常被认为是来解决“已知结果，分析原因”。不明白先验概率和后验概率的看下面这篇博客:
- 数据分类《二》贝叶斯分类
贝叶斯公式：
从公式中，我们会发现，右侧公式的分母，就是全概率公式。
百度百科针对这个公式的描述：公式中，事件Bi的概率为P(Bi)，事件Bi已发生条件下事件A的概率为P(A│Bi)，事件A发生条件下事件Bi的概率为P(Bi│A)。
说白了，就是根据结果去推各个因素下事件发生的概率。
这时候，大家可能会有个疑问，贝叶斯公式的原理和最大似然估计原理好像啊。没错，不要怀疑你的这个想法。准确来说，最大似然估计是用来辅助贝叶斯公式进行计算的。
我们来看贝叶斯公式，分母就是结果A发生的总概率，这个也叫结果，通常我们会先算出这个东西。
但是对于分子，P(Bi)是条件Bi发生的概率，P(A|Bi)是在条件Bi下，结果A 发生的概率。前者我们通过样本统计，一般不难得出来。但是后者，我们就很难得到。这时候，我们就把它转化为了估计参数，也就是将概率问题转化为了参数估计问题。如何进行参数估计呢，就用到了极大似然估计原理。
- 极大似然估计详解，写的太好了！
这篇博客讲解的比较明白！
4.交叉熵损失函数
L = − [ y l o g y ^ + ( 1 − y ) l o g ( 1 − y ^ ) ] L=-[ylog\ \hat y+(1-y)log\ (1-\hat y)] L=−[ylog y^+(1−y)log (1−y^)]
具体推到过程，可以参考下面的博客：
-
简单的交叉熵损失函数，你真的懂了吗？
-
损失函数 - 交叉熵损失函数
三、代码中的应用
# loss = fluid.layers.square_error_cost(predict,label)
loss = fluid.layers.cross_entropy(predict,label)
只需要将咱们前面使用的均方差损失函数换成下面的这个函数即可。