Python学习5之scikit-learn基础
Python学习5之scikit-learn基础
本系列文章用于以后编写代码直接调用某些代码,也用作一个学习后的记录,参考书籍为《Python数据分析与应用》,黄红梅,张良均主编,张凌,施兴,周东平副编,中国工信出版集团,人民邮电出版社,ISBN:9787115373045,文章附有代码和数据,学习起来较为容易
文章目录
- Python学习5之scikit-learn基础
- 前言
- 一、使用转换器处理数据
-
- 1.加载datasets模块中的数据集
- 2.数据集划分为训练集和测试集
- 3.使用转换器进行数据预处理和降维
- 二、构建病评价聚类模型
-
- 1.构建聚类模型
- 2.评价聚类模型
- 三、构建并评价分类模型
-
- 1.构建分类模型
- 2.评价分类模型
- 四、构建并评价回归模型
-
- 1.构建线性回归模型
- 2.评价回归模型
- 总结
前言
讲述包含多种机器学习算法的sklearn基础,在数据分析过程中快速建立模型,本节只讲述一些基础,对具体的模型算法介绍,之后会继续更新。
一、使用转换器处理数据
sklearn提供了model_selection模型选择模块,processing数据预处理模块和decompisition特征分解模块。通过这三个模块可以实现数据的预处理与模型构建前的数据标准化、二值化、数据集的分割、交叉验证和PCA降维等工作。
1.加载datasets模块中的数据集
sklearn中包含一些经典数据集,可以直接调用。加载后的数据集可以视为一个字典,几乎所有的sklearn数据集都可回忆使用data,target,feature_names,DESCR来获取数据集的数据,标签,特征名称和描述信息。
代码如下(示例):
#加载breast——cancer数据集
from sklearn.datasets import load_breast_cancer
cancer = load_breast_cancer()##将数据集赋值给iris变量
print('breast_cancer数据集的长度为:',len(cancer))
print('breast_cancer数据集的类型为:',type(cancer))
#数据集的内部信息获取
cancer_data = cancer['data']
print('breast_cancer数据集的数据为:','\n',cancer_data)
cancer_target = cancer['target'] ## 取出数据集的标签
print('breast_cancer数据集的标签为:\n',cancer_target)
cancer_names = cancer['feature_names'] ## 取出数据集的特征名
print('breast_cancer数据集的特征名为:\n',cancer_names)
cancer_desc = cancer['DESCR'] ## 取出数据集的描述信息
print('breast_cancer数据集的描述信息为:\n',cancer_desc)
2.数据集划分为训练集和测试集
在机器学习中极为常用的划分训练集与测试集,一般还有验证集。当数据集较少的时候,常用K折交叉验证法,使用sklearn中的model_selection模块中的train_test_split可以直接划分,很方便。
代码如下(示例):
#加载数据
from sklearn.datasets import load_breast_cancer
cancer = load_breast_cancer()##将数据集赋值给iris变量
cancer_data = cancer['data']
cancer_target = cancer['target'] ## 取出数据集的标签
# 训练测试集划分
print('原始数据集数据的形状为:',cancer_data.shape)
print('原始数据集标签的形状为:',cancer_target.shape)
from sklearn.model_selection import train_test_split
cancer_data_train, cancer_data_test,\
cancer_target_train, cancer_target_test = \
train_test_split(cancer_data, cancer_target,
test_size=0.2, random_state=42)
print('训练集数据的形状为:',cancer_data_train.shape)
print('训练集标签的形状为:',cancer_target_train.shape)
print('测试集数据的形状为:',cancer_data_test.shape)
print('测试集标签的形状为:',cancer_target_test.shape)
3.使用转换器进行数据预处理和降维
数据分析过程经常需要预处理数,通过转换器中的fit,transform和fit_transform可以较为简单实现,能够对Numpy数组进行标准化,归一化,二值化,PCA降维处理。
代码如下(示例):
#加载breast——cancer数据集
from sklearn.datasets import load_breast_cancer
cancer = load_breast_cancer()##将数据集赋值给cancer变量
cancer_data = cancer['data']
cancer_target = cancer['target'] ## 取出数据集的标签
#划分数据集
from sklearn.model_selection import train_test_split
cancer_data_train, cancer_data_test,\
cancer_target_train, cancer_target_test = \
train_test_split(cancer_data, cancer_target,
test_size=0.2, random_state=42)
##转化器的处理在于先生成规则,然后将规则分别应用于训练集和测试集
# 离差标准化
import numpy as np
from sklearn.preprocessing import MinMaxScaler
Scaler = MinMaxScaler().fit(cancer_data_train) ##生成规则
##将规则应用于训练集
cancer_trainScaler = Scaler.transform(cancer_data_train)
##将规则应用于测试集
cancer_testScaler = Scaler.transform(cancer_data_test)
print('离差标准化前训练集数据的最小值为:',np.min(cancer_data_train))
print('离差标准化后训练集数据的最小值为:',np.min(cancer_trainScaler))
print('离差标准化前训练集数据的最大值为:',np.max(cancer_data_train))
print('离差标准化后训练集数据的最大值为:',np.max(cancer_trainScaler))
print('离差标准化前测试集数据的最小值为:',np.min(cancer_data_test))
print('离差标准化后测试集数据的最小值为:',np.min(cancer_testScaler))
print('离差标准化前测试集数据的最大值为:',np.max(cancer_data_test))
print('离差标准化后测试集数据的最大值为:',np.max(cancer_testScaler))
# PCA降维
from sklearn.decomposition import PCA
pca_model = PCA(n_components=10).fit(cancer_trainScaler) ##生成规则
cancer_trainPca = pca_model.transform(cancer_trainScaler) ##将规则应用于训练集
cancer_testPca = pca_model.transform(cancer_testScaler) ##将规则应用于测试集
print('PCA降维前训练集数据的形状为:',cancer_trainScaler.shape)
print('PCA降维后训练集数据的形状为:',cancer_trainPca.shape)
print('PCA降维前测试集数据的形状为:',cancer_testScaler.shape)
print('PCA降维后测试集数据的形状为:',cancer_testPca.shape)
二、构建病评价聚类模型
聚类相关处理,主要是K-means聚类的构建和评价。
1.构建聚类模型
聚类算法有多种,按照算法类别有划分方法,层次分析方法,基于密度的方法,基于网格的方法常见的是Kmeans聚类(划分方法),在sklearn中各种方法都有,可以自行查询。
聚类算法需要使用估计器(Estimator),该估计器有fit和predict两个方法,fit主要用于训练算法,可以接受用于监督学习的训练集及标签两个参数,也可以接受无监督学习的数据;predict用于预测有监督学习的测试集标签,也可用于划分传入数据的类别。
代码如下(示例):
from sklearn.datasets import load_iris
from sklearn.preprocessing import MinMaxScaler
from sklearn.cluster import KMeans
iris = load_iris()
iris_data = iris['data'] ##提取数据集中的特征
iris_target = iris['target'] ## 提取数据集中的标签
iris_names = iris['feature_names'] ### 提取特征名
scale = MinMaxScaler().fit(iris_data)## 训练规则
iris_dataScale = scale.transform(iris_data) ## 应用规则
kmeans = KMeans(n_clusters = 3,
random_state=123).fit(iris_dataScale) ##构建并训练模型
print('构建的K-Means模型为:\n',kmeans)
result = kmeans.predict([[1.5,1.5,1.5,1.5]])
print('花瓣花萼长度宽度全为1.5的鸢尾花预测类别为:', result[0])
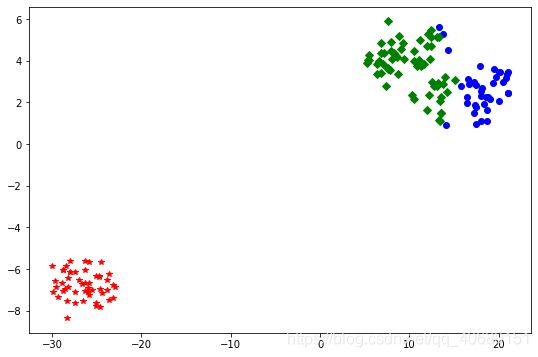
# 可视化
import pandas as pd
from sklearn.manifold import TSNE
import matplotlib.pyplot as plt
##使用TSNE进行数据降维,降成两维
tsne = TSNE(n_components=2,init='random',
random_state=177).fit(iris_data)
df=pd.DataFrame(tsne.embedding_) ##将原始数据转换为DataFrame
df['labels'] = kmeans.labels_ ##将聚类结果存储进df数据表
##提取不同标签的数据
df1 = df[df['labels']==0]
df2 = df[df['labels']==1]
df3 = df[df['labels']==2]
## 绘制图形
fig = plt.figure(figsize=(9,6)) ##设定空白画布,并制定大小
##用不同的颜色表示不同数据
plt.plot(df1[0],df1[1],'bo',df2[0],df2[1],'r*',
df3[0],df3[1],'gD')
plt.show() ##显示图片
2.评价聚类模型
聚类评价组内的相似性越大,组间的相似性越小,那么聚类效果就越好,使用Metrics模块可以评价。有ARIA评价法,AMI评价法,V-measure评分,FMI评价法,轮廓系数评价法,Calinski-Harabasz指数评价法,前四种需要真实值的配合才能评价优劣,后两种不需要,不过前四种说服力更高,除了轮廓系数法之外,都是得分越高越好,最高为1。
代码如下(示例):
#加载数据,训练模型
from sklearn.datasets import load_iris
from sklearn.preprocessing import MinMaxScaler
from sklearn.cluster import KMeans
iris = load_iris()
iris_data = iris['data'] ##提取数据集中的特征
iris_target = iris['target'] ## 提取数据集中的标签
iris_names = iris['feature_names'] ### 提取特征名
scale = MinMaxScaler().fit(iris_data)## 训练规则
iris_dataScale = scale.transform(iris_data) ## 应用规则
kmeans = KMeans(n_clusters = 3,
random_state=123).fit(iris_dataScale) ##构建并训练模型
# 使用FMI评价法评价聚类模型
from sklearn.metrics import fowlkes_mallows_score
for i in range(2,7):
##构建并训练模型
kmeans = KMeans(n_clusters = i,random_state=123).fit(iris_data)
score = fowlkes_mallows_score(iris_target,kmeans.labels_)
print('iris数据聚%d类FMI评价分值为:%f' %(i,score))
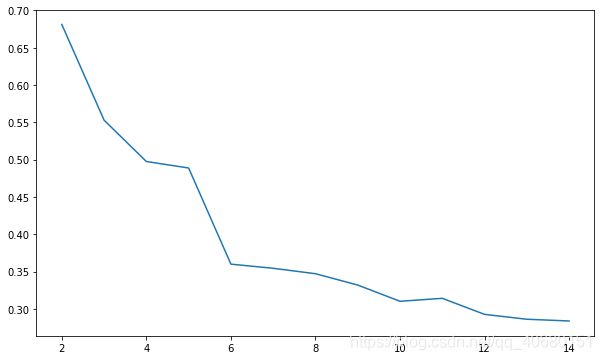
# 轮廓系数法评价
from sklearn.metrics import silhouette_score
import matplotlib.pyplot as plt
silhouettteScore = []
for i in range(2,15):
##构建并训练模型
kmeans = KMeans(n_clusters = i,random_state=123).fit(iris_data)
score = silhouette_score(iris_data,kmeans.labels_)
silhouettteScore.append(score)
plt.figure(figsize=(10,6))
plt.plot(range(2,15),silhouettteScore,linewidth=1.5, linestyle="-")
plt.show()
# CH指数评价法评价
from sklearn.metrics import calinski_harabaz_score
for i in range(2,7):
##构建并训练模型
kmeans = KMeans(n_clusters = i,random_state=123).fit(iris_data)
score = calinski_harabaz_score(iris_data,kmeans.labels_)
print('iris数据聚%d类calinski_harabaz指数为:%f'%(i,score))
在轮廓系数法中可以绘图来看,最陡峭的地方是合适的聚类点,与PCA降维的碎石图相似。本例聚类为三类更好。
三、构建并评价分类模型
分类是有监督学习,也比较常用,本例讲解SVM分类,除此之外还有fisher分类,贝叶斯分类,K最近邻分类,随机森林分类等多种分类方法。
1.构建分类模型
采用SVM模型分类
代码如下(示例):
## 加载所需的函数,
import numpy as np
from sklearn.datasets import load_breast_cancer
from sklearn.svm import SVC
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
cancer = load_breast_cancer()
cancer_data = cancer['data']
cancer_target = cancer['target']
cancer_names = cancer['feature_names']
## 将数据划分为训练集测试集
cancer_data_train,cancer_data_test, \
cancer_target_train,cancer_target_test = \
train_test_split(cancer_data,cancer_target,
test_size = 0.2,random_state = 22)
## 数据标准化
stdScaler = StandardScaler().fit(cancer_data_train)
cancer_trainStd = stdScaler.transform(cancer_data_train)
cancer_testStd = stdScaler.transform(cancer_data_test)
## 建立SVM模型
svm = SVC().fit(cancer_trainStd,cancer_target_train)
print('建立的SVM模型为:\n',svm)
## 预测训练集结果
cancer_target_pred = svm.predict(cancer_testStd)
print('预测前20个结果为:\n',cancer_target_pred[:20])
# 分类结果的混淆矩阵与准确率
## 求出预测和真实一样的数目
true = np.sum(cancer_target_pred == cancer_target_test )
print('预测对的结果数目为:', true)
print('预测错的的结果数目为:', cancer_target_test.shape[0]-true)
print('预测结果准确率为:', true/cancer_target_test.shape[0])
2.评价分类模型
仅有对预测集的分类准确率并不能很好的反映模型的性能,为了有效表明性能,需要结合真实值计算准确率,召回率,F1值和Cohen’s Kappa系数等指标衡量,以及ROC曲线,更为常用。
代码如下(示例):
## 加载所需的函数,
import numpy as np
from sklearn.datasets import load_breast_cancer
from sklearn.svm import SVC
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
cancer = load_breast_cancer()
cancer_data = cancer['data']
cancer_target = cancer['target']
cancer_names = cancer['feature_names']
## 将数据划分为训练集测试集
cancer_data_train,cancer_data_test, \
cancer_target_train,cancer_target_test = \
train_test_split(cancer_data,cancer_target,
test_size = 0.2,random_state = 22)
## 数据标准化
stdScaler = StandardScaler().fit(cancer_data_train)
cancer_trainStd = stdScaler.transform(cancer_data_train)
cancer_testStd = stdScaler.transform(cancer_data_test)
## 建立SVM模型
svm = SVC().fit(cancer_trainStd,cancer_target_train)
## 预测训练集结果
cancer_target_pred = svm.predict(cancer_testStd)
print('预测前20个结果为:\n',cancer_target_pred[:20])
#分类模型各种评价方法(系数类)
from sklearn.metrics import accuracy_score,precision_score, \
recall_score,f1_score,cohen_kappa_score
print('使用SVM预测breast_cancer数据的准确率为:',
accuracy_score(cancer_target_test,cancer_target_pred))
print('使用SVM预测breast_cancer数据的精确率为:',
precision_score(cancer_target_test,cancer_target_pred))
print('使用SVM预测breast_cancer数据的召回率为:',
recall_score(cancer_target_test,cancer_target_pred))
print('使用SVM预测breast_cancer数据的F1值为:',
f1_score(cancer_target_test,cancer_target_pred))
print('使用SVM预测breast_cancer数据的Cohen’s Kappa系数为:',
cohen_kappa_score(cancer_target_test,cancer_target_pred))
# 分类模型评价报告
from sklearn.metrics import classification_report
print('使用SVM预测iris数据的分类报告为:','\n',
classification_report(cancer_target_test,
cancer_target_pred))
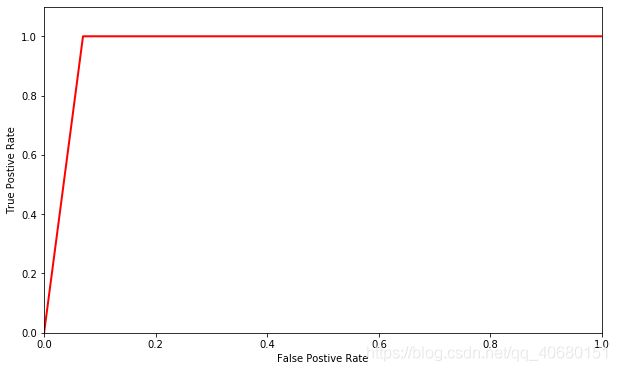
# ROC曲线绘制
from sklearn.metrics import roc_curve
import matplotlib.pyplot as plt
## 求出ROC曲线的x轴和y轴
fpr, tpr, thresholds = \
roc_curve(cancer_target_test,cancer_target_pred)
plt.figure(figsize=(10,6))
plt.xlim(0,1) ##设定x轴的范围
plt.ylim(0.0,1.1) ## 设定y轴的范围
plt.xlabel('False Postive Rate')
plt.ylabel('True Postive Rate')
plt.plot(fpr,tpr,linewidth=2, linestyle="-",color='red')
plt.show()
四、构建并评价回归模型
回归与分类的区别仅在于分类的标签离散,回归的标签连续,大致原理是一样的。常见的回归模型有 线性回归,Logistic回归,岭回归,主成分回归等多种回归。Sklearn中都有包,自行查询。
1.构建线性回归模型
以boston数据集做线性回归。
代码如下(示例):
# 构建线性回归模型
##加载所需函数
from sklearn.linear_model import LinearRegression
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
## 加载boston数据
boston = load_boston()
X = boston['data']
y = boston['target']
names = boston['feature_names']
## 将数据划分为训练集测试集
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size = 0.2,random_state=125)
## 建立线性回归模型
clf = LinearRegression().fit(X_train,y_train)
print('建立的LinearRegression模型为:','\n',clf)
## 预测训练集结果
y_pred = clf.predict(X_test)
print('预测前20个结果为:','\n',y_pred[:20])
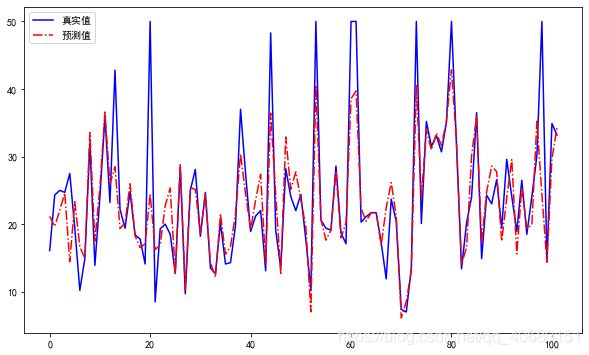
# 可视化
import matplotlib.pyplot as plt
from matplotlib import rcParams
rcParams['font.sans-serif'] = 'SimHei'
fig = plt.figure(figsize=(10,6)) ##设定空白画布,并制定大小
##用不同的颜色表示不同数据
plt.plot(range(y_test.shape[0]),y_test,color="blue", linewidth=1.5, linestyle="-")
plt.plot(range(y_test.shape[0]),y_pred,color="red", linewidth=1.5, linestyle="-.")
plt.legend(['真实值','预测值'])
plt.show() ##显示图片
2.评价回归模型
回归模型评价与分类不同,虽然都是真实值进行评价,但由于回归模型的预测结果与真实值都是连续的,所以不能采用F1等指标,需要用平均绝对误差,均方误差,中值绝对误差,可解释方差值, R 2 R^2 R2值来评价。可解释方差和 R 2 R^2 R2是越接近1越好,其他都是越接近0越好。
代码如下(示例):
# 构建线性回归模型
##加载所需函数
from sklearn.linear_model import LinearRegression
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
## 加载boston数据
boston = load_boston()
X = boston['data']
y = boston['target']
names = boston['feature_names']
## 将数据划分为训练集测试集
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size = 0.2,random_state=125)
## 建立线性回归模型
clf = LinearRegression().fit(X_train,y_train)
print('建立的LinearRegression模型为:','\n',clf)
## 预测训练集结果
y_pred = clf.predict(X_test)
print('预测前20个结果为:','\n',y_pred[:20])
from sklearn.metrics import explained_variance_score,\
mean_absolute_error,\
mean_squared_error,\
median_absolute_error,r2_score
print('Boston数据线性回归模型的平均绝对误差为:',
mean_absolute_error(y_test,y_pred))
print('Boston数据线性回归模型的均方误差为:',
mean_squared_error(y_test,y_pred))
print('Boston数据线性回归模型的中值绝对误差为:',
median_absolute_error(y_test,y_pred))
print('Boston数据线性回归模型的可解释方差值为:',
explained_variance_score(y_test,y_pred))
print('Boston数据线性回归模型的R方值为:',
r2_score(y_test,y_pred))
总结
提示:本文章简单介绍了sklearn的使用。