2022年华数杯C题插层熔喷非织造材料的性能控制研究数学建模论文及程序
2022年华数杯C题插层熔喷非织造材料的性能控制研究
仅献给读者的你
原题再现:
熔喷非织造材料是口罩生产的重要原材料,具有很好的过滤性能,其生产工艺简单、成本低、质量轻等特点,受到国内外企业的广泛关注。但是,由于熔喷非织造材料纤维非常细,在使用过程中经常因为压缩回弹性差而导致其性能得不到保障。因此,科学家们创造出插层熔喷法,即通过在聚丙烯(PP)熔喷制备过程中将涤纶(PET)短纤等纤维插入熔喷纤维流,制备出了“Z型”结构的插层熔喷非织造材料。插层熔喷非织造材料制备工艺参数较多,参数之间还存在交互影响,加上插层气流之后更为复杂,因此,通过工艺参数(接收距离和热空气速度)决定结构变量(厚度、孔隙率、压缩回弹性),而由结构变量决定最终产品性能(过滤阻力、过滤效率、透气性)的研究也变得较为复杂。如果能分别建立工艺参数与结构变量、结构变量和产品性能之间的关系模型,则有助于为产品性能调控机制的建立提供一定的理论基础。请查阅相关文献,了解专业背景,研究题目数据,回答下列问题。
1. 请研究插层后结构变量、产品性能的变化规律,并分析插层率对于这些变化是否
有影响?
2. 请研究工艺参数与结构变量之间的关系。表1给了8个工艺参数组合,请将预测的
结构变量数据填入表1中。

3. 请研究结构变量与产品性能的关系,以及结构变量之间、产品性能之间的关系。结合第二问,研究当工艺参数为多少时,产品的过滤效率将会达到最高?
4. 实际上,产品生产需要兼顾各方面的条件和要求。如接收距离不大可能大于100cm,热空气速度也不大可能大于2000 r/min。按照应用的要求,厚度尽量不要超过3mm,压缩回弹性率尽量不要低于85%。另外,为了防止熔喷非织造过滤材料因过滤阻力大使得大量颗粒堵塞孔隙而致使过滤效率迅速下降的现象发生,产品是需要同时追求过滤效率高和过滤阻小的目标的。请问工艺参数为多少时,能够使得过滤效率尽量的高的同时力求过滤阻力尽量的小?
专业术语简要解释:
插层率%:将卷曲高弹、力学性能优异的涤纶(PET)短纤插入聚丙烯(PP)切片(非织造材料所用到的一种聚合物)中的重量比例。插层是一种混合的方式。
接收距离cm:实验时溶液喷射点到接收喷射过来的溶液位置的距离。
热空气速度 r/min:溶液在空气中喷射的速度。
厚度mm:形成熔喷非织造材料的厚度。
孔隙率%:形成熔喷非织造材料中空隙占材料体积的比率。
压缩回弹性%:反抗压缩的回弹能力。弹性越大说明抗压能力越强。
过滤阻力Pa:阻碍物质颗粒通过熔喷非织造材料的能力。
过滤效率%:物质颗粒通过熔喷非织造材料的比例。
透气性mm/s:空气贯穿熔喷非织造材料的通畅性。
数据解释:
1.“C题数据.xlsx”中的data1中给出了25组对照实验。第一列为实验工艺条件组号,
组号所对应的工艺参数组合见data2。其中1#表示未插层材料(普通熔喷材料),2#表示
插层熔喷材料。
2.“C题数据.xlsx”中的data3给出了插层率固定的条件下的,不同工艺参数组合的
材料结构变量数据和产品性能数据。每个组合实验重复了三次。
模型的建立与求解:
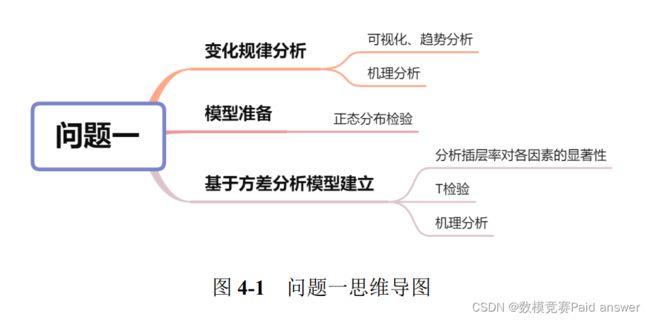
问题一描述与分析
问题一可以分为两个部分,第一问要求分析插层后结构变量与产品性能的变化规律,第二问要求研究插层率对于结构变量和产品性能的变化的影响。针对第一部分,要探寻变化规律,需要将同一组在插层前后的结构变量和产品性能做纵向对比,可通过对数据的可视化处理,绘制折线图。根据图像的走势和前后对比分析出变化规律。
针对第二部分,首先对数据进行预处理,检验各项指标数据是否符合正态分布,各项指标数据均可接受为正态分布,采用方差分析的方法对插层率与各项指标之间的相关程度计算,对比总结出插层率对结构变量和产品性能变化的影响,得出具有可靠性的结果。
产品性能的三个指标变化规律为:过滤阻力、过滤效率和透气性。在插层后普遍得到小幅度的改善,受插层的影响较小。具体表现在,插层后,平均每组的过滤阻力降低了 5.62708 Pa,每组的过滤率效率提升了 14.39464%,每组的透气性增加了 74.5304 mm/s。
产品的性能主要由结构变量决定,虽然插层对结构变量有影响,但并不是影响产品性能的决定性因素,因此插层后的产品性能得到提升,但提升的幅度较小。
通过查阅相关资料,对上述变化规律做出相关解释:
机理分析:熔喷非织造材料具有纤维超细、比表面积大、孔径小、孔隙率高等特点[1]。插层处理后,在产品之间增加了材料,因而材料的厚度会增大;在插层过程中,由于材料本身特性与热风的作用,使得材料可以均匀分布,有效防止了材料的堆积与阻塞,从而提高了孔隙率;由于改进了材料,在聚丙烯 (PP) 熔喷制备过程中将涤纶 (PET)短纤等纤维插入熔喷纤维流,材料的韧性得到有效的提高,因此产品的压缩回弹率得到了提高。
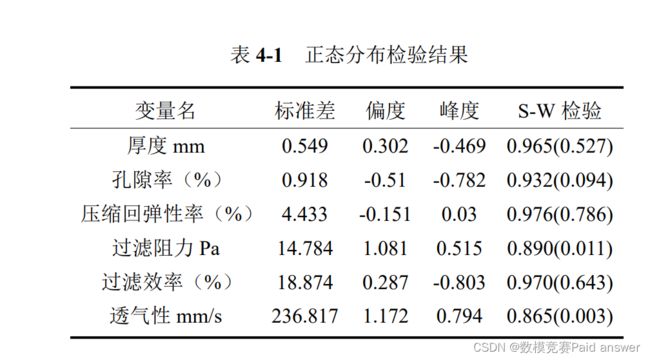
由于进行方差分析样本需要满足正态分布,本文通过 Shapiro-Wilk 检验法对样本数据进行正态检验。Shapiro-Wilk 检验法适用于小样本数据,先假设 H0 为随机变量服从正态分布,H1 为该变量不服从正态分布,计算出 Wilk 统计量之后,得到相应的 p 值,并将 p 值与 0.01 比较,若小于 0.1,若样本峰度绝对值小于 10 并且偏度绝对值小于 3,结合正态分布直方图或者 QQ 图可以描述为基本符合正态分布,若不满足可以拒绝原假设。若 p 值大于 0.01,不可以拒绝原假设。本文对结构变量、产品性能中各个类别数据进行正态分布检验,得到结果如下:
LightGBM 算法基于决策树的继承学习方法,是梯度提升树的一钟实现[3]。该算法的每次迭代都会在之前生成的所有学习器基础上新生成一个学习器, 然后利用梯度下降的方法,使损失数逐渐减小, 最终得到一个最好效果的学习器用作预测模型。相比传统的 XGBoost 算法,LightGBM 算法利用单边梯度采样和互斥特征捆绑,通过使用 GOSS可以减少大量只具有小梯度的数据实例,在计算信息增益的时候只利用剩下的具有高梯度的数据即可,减少了其时间和空间的复杂度,提高了预测评价的准确率。LightGBM 算法的核心在于决策树的生长策略,使用了带有深度限制的按叶子生长
方法,即:
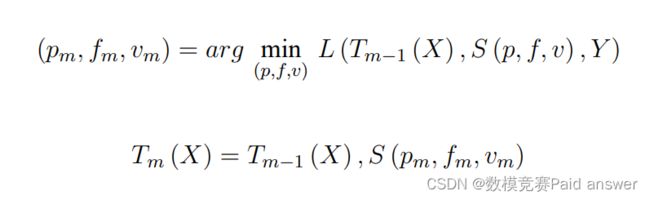
LightGBM 算法利用直方图算法,将连续的特征离散化为 k 个离散特征,同时构造一个宽度为 k 的直方图用于统计信息(含有 k 个 bin )。利用直方图方法无需遍历数据,只需要遍历 k 个 bin 即可找到最佳分裂点。我们希望损失函数越小越好,因此对一个叶子节点进行分裂,分裂前后的增益定义为:
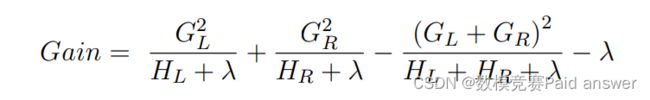

结合第二问,建立梯度提升回归树模型,针对附件数据进行训练,以过滤效率最高为目标,经过迭代训练得到过滤效率最高时的工艺参数。GBRT 模型是 Boosting 算法的一种,通过利用训练样本集进行迭代产生很多颗不同的弱回归树来集成形成强回归树模型来不断逼近学习目标的一个过程[5]。本节首先给出预测模型构建的总体思路,然后阐述任意一颗弱决策树的构造方法。梯度提升回归树流程如下:

计算前文得到的偏导数在当前函数模型 Fm−1 (x) 中的值,并将该值乘以损失函数的负梯度 h (x) ,以此来近似模拟 F (x) 的预测残差 rmi :

完整论文及程序,均都过程详细完成

程序代码
import numpy as np
import pandas as pd
import lightgbm as lgb
from sklearn.model_selection import KFold
from sklearn.metrics import mean_squared_error
# 读取数据集
train = pd.read_excel("train.xlsx",sheet_name='Sheet2')
test = pd.read_excel("test.xlsx")
# 构建训练集和验证集
X = train.drop(columns=['厚度mm'], axis=1).values
y = train['厚度mm'].values
# K折交叉验证
kf = KFold(n_splits=10)
rmse_scores = []
for train_indices, test_indices in kf.split(X):
X_train, X_test = X[train_indices], X[test_indices]
y_train, y_test = y[train_indices], y[test_indices]
# 初始化模型
LGBR = lgb.LGBMRegressor() # 基模型
# 训练/fit拟合
LGBR.fit(X_train, y_train)
# 预测
y_pred = LGBR.predict(X_test)
# 评估
rmse = mean_squared_error(y_test, y_pred)
# 累计结果
rmse_scores.append(rmse)
print("rmse scores : ", rmse_scores)
print(f'average rmse scores : {np.mean(rmse_scores)}')
train_data = lgb.Dataset(X_train, label=y_train) # 训练集
test_data = lgb.Dataset(X_test, label=y_test, reference=train_data) # 验证集
# 参数
params = {
'objective':'regression', # 目标任务
'metric':'rmse', # 评估指标
'learning_rate':0.1, # 学习率
'max_depth':15, # 树的深度
'num_leaves':20, # 叶子数
}
# 创建模型对象
model = lgb.train(params=params,
train_set=train_data,
num_boost_round=300,
early_stopping_rounds=30,
valid_names=['test'],
valid_sets=[test_data])
score = model.best_score['test']['rmse']
score
test_pred = model.predict(test.drop('Id',axis=1).values)
厚度:
import numpy
import pandas
from spsspro.algorithm import supervised_learning
data_x = pandas.DataFrame({
"A": numpy.random.random(size=100),
"B": numpy.random.random(size=100)
})
data_y = pandas.Series(data=numpy.random.choice([1, 2], size=100), name="C")
result = supervised_learning.lightgbm_regression(data_x=data_x, data_y=data_y)
print(result)
孔隙率:
import numpy
import pandas
from spsspro.algorithm import supervised_learning
data_x = pandas.DataFrame({
"A": numpy.random.random(size=100),
"B": numpy.random.random(size=100)
})
data_y = pandas.Series(data=numpy.random.choice([1, 2], size=100), name="C")
result = supervised_learning.lightgbm_regression(data_x=data_x, data_y=data_y)
print(result)
压缩:
import numpy
import pandas
from spsspro.algorithm import supervised_learning
#生成案例数据
data_x = pandas.DataFrame({
"A": numpy.random.random(size=100),
"B": numpy.random.random(size=100)
})
data_y = pandas.Series(data=numpy.random.choice([1, 2], size=100), name="C")
result = supervised_learning.lightgbm_regression(data_x=data_x, data_y=data_y)
print(result)