【机器学习】一文读懂异常检测 LOF 算法(Python代码)
本篇介绍一个经典的异常检测算法:局部离群因子(Local Outlier Factor),简称LOF算法。
背景
Local Outlier Factor(LOF)是基于密度的经典算法(Breuning et. al. 2000), 文章发表于 SIGMOD 2000, 到目前已经有 3000+ 的引用。
在 LOF 之前的异常检测算法大多是基于统计方法的,或者是借用了一些聚类算法用于异常点的识别(比如 ,DBSCAN,OPTICS)。这些方法都有一些不完美的地方:
基于统计的方法:通常需要假设数据服从特定的概率分布,这个假设往往是不成立的。
聚类方法:通常只能给出 0/1 的判断(即:是不是异常点),不能量化每个数据点的异常程度。
相比较而言,基于密度的LOF算法要更简单、直观。它不需要对数据的分布做太多要求,还能量化每个数据点的异常程度(outlierness)。
下面开始正式介绍LOF算法。
LOF 算法
首先,基于密度的离群点检测方法有一个基本假设:非离群点对象周围的密度与其邻域周围的密度类似,而离群点对象周围的密度显著不同于其邻域周围的密度。
什么意思呢?看下面图片感受下。
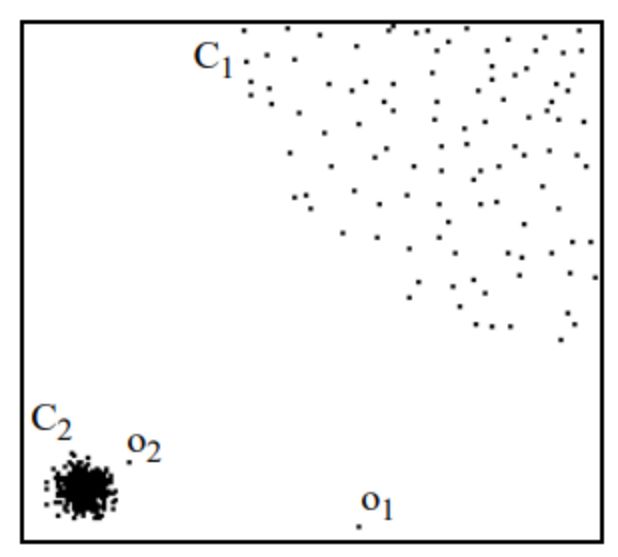
集群 C1 包含了 400 多个点,集群 C2 包含 100 个点。C1 和 C2 都是一类集群点,区别是 C1 位置比较集中,或者说密度比较大。而像 o1、o2点均为异常点,因为基于我们的假设,这两个点周围的密度显著不同于周围点的密度。
LOF 就是基于密度来判断异常点的,通过给每个数据点都分配一个依赖于邻域密度的离群因子 LOF,进而判断该数据点是否为离群点。 如果 ,则该点为离群点,如果 ,则该点为正常数据点。
那么什么是LOF呢?
了解LOF前,必须先知道一下3个基本概念,因为LOF是基于这几个概念而来的。
1. k邻近距离
在距离数据点 最近的几个点中,第 个最近的点跟点 之间的距离称为点 的 K-邻近距离,记为 k-distance (p),公式如下:
点 为距离点 最近的第 个点。

比如上图中,距离点 最近的第 个点是点 。
这里的距离计算可以采用欧式距离、汉明距离、马氏距离等等。比如用欧式距离的计算公式如下:
这里的重点是找到第 个最近的那个点,然后带公式计算距离。
2. k距离领域
以点 为圆心,以k邻近距离 为半径画圆,这个圆以内的范围就是k距离领域,公式如下:
还是上图所示,假设k=4,那么点 1-6 均是邻域范围内的点。
3. 可达距离
这个可达距离大家需要留意点,点 到点 的第 可达距离:
这里计算 到点 的第 可达距离,但是要以点 为中心,取一个最大值,也就是在点 与 的距离、距离点 最近的第 个点距离中取较大的一个,如图下所示。
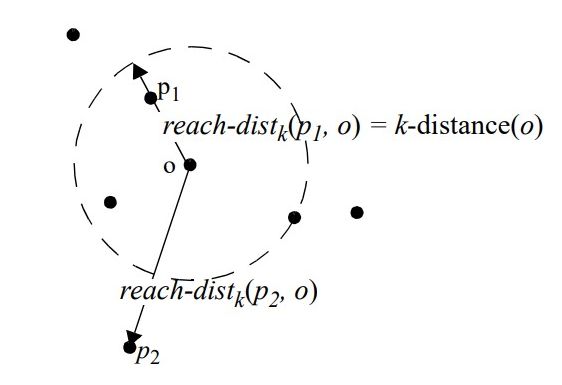
距离 远,那么两者之间的可达距离就是它们的实际距离。如果距离足够近,如点 ,实际距离将被 的 距离代替。所有 接近 的统计波动 可以显著减少,这可以通过参数 来控制, 值越高,同一邻域内的点的可达距离越相似。
4. 局部可达密度
先给出公式,然后再说明密度的含义。
数据点 的局部可达密度就是基于 的最近邻的平均可达距离的倒数。距离越大,密度越小。
5. 局部异常因子
根据局部可达密度的定义,如果一个数据点跟其他点比较疏远的话,那么显然它的局部可达密度就小。但LOF算法衡量一个数据点的异常程度,并不是看它的绝对局部密度,而是看它跟周围邻近的数据点的相对密度。
这样做的好处是可以允许数据分布不均匀、密度不同的情况。局部异常因子即是用局部相对密度来定义的。数据点 的局部相对密度(局部异常因子)为点 邻域内点的平均局部可达密度跟数据点 的局部可达密度的比值,即:
LOF算法流程
了解了 LOF 的定义以后,整个算法也就显而易见了:
对于每个数据点,计算它与其它所有点的距离,并按从近到远排序;
对于每个数据点,找到它的 k-nearest-neighbor,计算 LOF 得分;
如果LOF值越大,说明越异常,反之如果越小,说明越趋于正常。

LOF优缺点
优点
LOF 的一个优点是它同时考虑了数据集的局部和全局属性。异常值不是按绝对值确定的,而是相对于它们的邻域点密度确定的。当数据集中存在不同密度的不同集群时,LOF表现良好,比较适用于中等高维的数据集。
缺点
LOF算法中关于局部可达密度的定义其实暗含了一个假设,即:不存在大于等于 k 个重复的点。
当这样的重复点存在的时候,这些点的平均可达距离为零,局部可达密度就变为无穷大,会给计算带来一些麻烦。在实际应用时,为了避免这样的情况出现,可以把 k-distance 改为 k-distinct-distance,不考虑重复的情况。或者,还可以考虑给可达距离都加一个很小的值,避免可达距离等于零。
另外,LOF 算法需要计算数据点两两之间的距离,造成整个算法时间复杂度为 。为了提高算法效率,后续有算法尝试改进。FastLOF (Goldstein,2012)先将整个数据随机的分成多个子集,然后在每个子集里计算 LOF 值。对于那些 LOF 异常得分小于等于 1 的,从数据集里剔除,剩下的在下一轮寻找更合适的 nearest-neighbor,并更新 LOF 值。
Python 实现 LOF
有两个库可以计算LOF,分别是PyOD和Sklearn,下面分别介绍。
使用pyod自带的方法生成200个训练样本和100个测试样本的数据集。正态样本由多元高斯分布生成,异常样本是使用均匀分布生成的。
训练和测试数据集都有 5 个特征,10% 的行被标记为异常。并且在数据中添加了一些随机噪声,让完美分离正常点和异常点变得稍微困难一些。
from pyod.utils.data import generate_data
import numpy as np
X_train, y_train, X_test, y_test = \
generate_data(n_train=200,
n_test=100,
n_features=5,
contamination=0.1,
random_state=3)
X_train = X_train * np.random.uniform(0, 1, size=X_train.shape)
X_test = X_test * np.random.uniform(0,1, size=X_test.shape)PyOD
下面将训练数据拟合了 LOF 模型并将其应用于合成测试数据。
在 PyOD 中,有两个关键方法:decision_function 和 predict。
decision_function:返回每一行的异常分数
predict:返回一个由 0 和 1 组成的数组,指示每一行被预测为正常 (0) 还是异常值 (1)
from pyod.models.lof import LOF
clf_name = 'LOF'
clf = LOF()
clf.fit(X_train)
test_scores = clf.decision_function(X_test)
roc = round(roc_auc_score(y_test, test_scores), ndigits=4)
prn = round(precision_n_scores(y_test, test_scores), ndigits=4)
print(f'{clf_name} ROC:{roc}, precision @ rank n:{prn}')
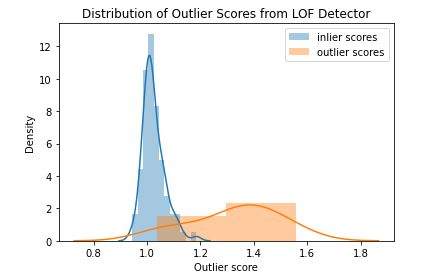
>> LOF ROC:0.9656, precision @ rank n:0.8可以通过 LOF 模型方法查看 LOF 分数的分布。在下图中看到正常数据(蓝色)的分数聚集在 1.0 左右。离群数据点(橙色)的得分均大于 1.0,一般高于正常数据。
Sklearn
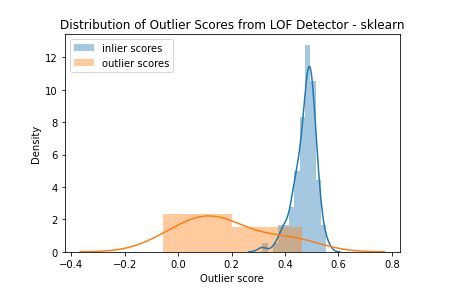
在scikit-learn中实现 LOF 进行异常检测时,有两种模式选择:异常检测模式 (novelty=False) 和 novelty检测模式 (novelty=True)。
在异常检测模式下,只有fit_predict生成离群点预测的方法可用。可以使用negative_outlier_factor_属性检索训练数据的异常值分数,但无法为未见过的数据生成分数。模型会根据contamination参数(默认值为 0.1)自动选择异常值的阈值。
import matplotlib.pyplot as plt
detector = LOF()
scores = detector.fit(X_train).decision_function(X_test)
sns.distplot(scores[y_test==0], label="inlier scores")
sns.distplot(scores[y_test==1], label="outlier scores").set_title("Distribution of Outlier Scores from LOF Detector")
plt.legend()
plt.xlabel("Outlier score")在novelty检测模式下,只有decision_function用于生成异常值可用。fit_predict方法不可用,但predict方法可用于生成异常值预测。
clf = LocalOutlierFactor(novelty=True)
clf = clf.fit(X_train)
test_scores = clf.decision_function(X_test)
test_scores = -1*test_scores
roc = round(roc_auc_score(y_test, test_scores), ndigits=4)
prn = round(precision_n_scores(y_test, test_scores), ndigits=4)
print(f'{clf_name} ROC:{roc}, precision @ rank n:{prn}')该模式下模型的异常值分数被反转,异常值的分数低于正常值。
实战系列的全部完整代码可见:https://github.com/xiaoyusmd/PythonDataScience
原创不易,欢迎点赞、在看。
关于LOF的原论文可以在公众号回复:LOF 获取。
参考:
https://pub.towardsai.net/an-in-depth-guide-to-local-outlier-factor-lof-for-outlier-detection-in-python-5a6f128e5871 https://zhuanlan.zhihu.com/p/28178476 https://mp.weixin.qq.com/s/SHYNjtqCo-Ue3lezdVk1jA https://www.cnblogs.com/xzydn/p/14408758.html
往期精彩回顾
适合初学者入门人工智能的路线及资料下载机器学习及深度学习笔记等资料打印机器学习在线手册深度学习笔记专辑《统计学习方法》的代码复现专辑
AI基础下载黄海广老师《机器学习课程》视频课黄海广老师《机器学习课程》711页完整版课件本站qq群955171419,加入微信群请扫码:
