深度学习 | pytorch（二）

记于2021年端午节

十、基本运算

1、加减乘除add / minus / multiply / divid

a = torch.rand(3,4)
a

b = torch.rand(4)
b

a+b

torch.add(a,b)

torch.all(torch.eq(a-b,torch.sub(a,b)))

torch.all(torch.eq(a*b,torch.mul(a,b)))

torch.all(torch.eq(a/b,torch.div(a,b)))

#说明数学运算符和英文名是等同的，建议直接使用运算符

2、matmul

（1）2d tensor matmul

torch.mm 只适用于2d，不推荐使用
torch.matmul推荐,也可以直接使用@

a = torch.tensor([[3.,3.],[3.,3.]])
a

b = torch.ones(2,2)
b

torch.mm(a,b)

torch.matmul(a,b)

a@b

实现降维(4,784)=>(4,512)：

a = torch.rand(4,784)
x = torch.rand(4,784)
w = torch.rand(512,784)  #channel-out,channel-in
(x@w.t()).shape          #.t()只适用于2d的tensor，如果是高维的，要使用transpose

神经网络可以理解为tensor，矩阵的相乘相加

（2）>2d tensor matmul

a = torch.rand(4,3,28,64)
b = torch.rand(4,3,64,32)
a.shape,b.shape,torch.matmul(a,b).shape#前面两维保持不变，后边两维进行运算

b1 = torch.rand(4,1,64,32)
a.shape,b.shape,torch.matmul(a,b1).shape#使用了broadcast和矩阵乘法

b2 = torch.rand(4,64,32)
torch.matmul(a,b2)

3、矩阵次方

①.pow(阶数)

创建一个全部都是3的shape为[2,2]的矩阵：

a = torch.full([2,2],3.)
a.pow(2)    

a**2

②平方根 .sqrt()

aa = a**2
aa.sqrt() 

③平方根的倒数 .rsqrt()

aa.rsqrt() 

不论是平方还是开方都可以这样写：

aa**(0.5) 

4、对数运算

①.exp()

a = torch.exp(torch.ones(2,2))  #以e为底
a

tensor([[2.7183, 2.7183],
[2.7183, 2.7183]])

②.log(以谁为底)

torch.log(a)   #以谁为底就写几

tensor([[1., 1.],
        [1., 1.]])

5、近似解 approximation

①向下取整 .floor()

②向上取整 .ceil()

③裁剪浮点数的整数部分 .trunc()

④裁剪浮点数的小数部分 .frac()

a = torch.tensor(3.14)
a

tensor(3.1400)

a.floor(),a.ceil(),a.trunc(),a.frac()

(tensor(3.), tensor(4.), tensor(3.), tensor(0.1400))

⑤四舍五入 .round()

a = torch.tensor(3.499)
a.round()  #四舍五入

tensor(3.)

a = torch.tensor(3.5)
a.round()

tensor(4.)

6、梯度裁剪 .clamp()

①.clamp(min) 把小于min的值统一变为min
②.clamp(min, max) 把小于min的值统一变为min, 把大于max的值统一变为max

grad = torch.rand(2,3)*15
grad

tensor([[14.1900, 14.6534, 6.0197],
[ 7.3536, 5.4166, 11.4699]])

梯度最大值：

grad.max()

tensor(14.6534)

梯度中值：

grad.median()

tensor(7.3536)

grad.clamp(10)  #(min)，把小于10的统一变为10

tensor([[14.1900, 14.6534, 10.0000],
[10.0000, 10.0000, 11.4699]])

grad

tensor([[14.1900, 14.6534, 6.0197],
[ 7.3536, 5.4166, 11.4699]])

grad.clamp(0,10)     #(min,max)

tensor([[10.0000, 10.0000, 6.0197],
[ 7.3536, 5.4166, 10.0000]])

十一、属性统计

1、norm范数

a = torch.full([8],1.)
a,a.dtype

(tensor([1., 1., 1., 1., 1., 1., 1., 1.]), torch.float32)

b = a.view(2,4)
b,b.dtype

(tensor([[1., 1., 1., 1.],
[1., 1., 1., 1.]]),
torch.float32)

c = a.view(2,2,2)
c,c.dtype

(tensor([[[1., 1.],
[1., 1.]],
[[1., 1.],
[1., 1.]]]),
torch.float32)

①1范数是绝对值的求和

应为浮点型，不能为整型。

a.norm(1),b.norm(1),c.norm(1) 

(tensor(8.), tensor(8.), tensor(8.))

②2范数是所有元素绝对值的平方和 开根号：

a.norm(2),b.norm(2),c.norm(2) 

(tensor(2.8284), tensor(2.8284), tensor(2.8284))

第1维元素的1范数：

b.norm(1,dim=1) 

tensor([4., 4.])

第1维元素的2范数：

b.norm(2,dim=1)

tensor([2., 2.])

第0维元素的1范数：

c.norm(1,dim=0)

tensor([[2., 2.],
[2., 2.]])

第0维元素的2范数：

c.norm(2,dim=0)

tensor([[1.4142, 1.4142],
[1.4142, 1.4142]])

2、min, max, mean, sum, prod

a = torch.arange(8).view(2,4).float()
a

tensor([[0., 1., 2., 3.],
[4., 5., 6., 7.]])

a.min(),a.max(),a.mean(),a.sum(),a.prod() #最小值，最大值，中值，求和，连乘

(tensor(0.), tensor(7.), tensor(3.5000), tensor(28.), tensor(0.))

a.argmax(),a.argmin() #最大值的索引，最小值的索引。先把a拉平，然后给出索引。

(tensor(7), tensor(0))

a.argmax(dim=0),a.argmin(dim=0)#列最大/小值所在的行索引

(tensor([1, 1, 1, 1]), tensor([0, 0, 0, 0]))

a.argmax(dim=1),a.argmin(dim=1)#行最大/小值所在的列索引

(tensor([3, 3]), tensor([0, 0]))

3、dim, keepdim

a的size：tensor([[0., 1., 2., 3.], [4., 5., 6., 7.]])

a.max(dim=1)

torch.return_types.max(
values=tensor([3., 7.]),
indices=tensor([3, 3]))

a.max(dim=1,keepdim=True)

torch.return_types.max(
values=tensor([[3.],
[7.]]),
indices=tensor([[3],
[3]]))

a.argmax(dim=1,keepdim=True)

tensor([[3],
[3]])

4、topk or k-th

①最大的k个 .topk

a

tensor([[0., 1., 2., 3.],
[4., 5., 6., 7.]])

第1维上最大的3个数从大到小的值与其所对应的索引：

a.topk(3,dim=1)   

torch.return_types.topk(
values=tensor([[3., 2., 1.],
[7., 6., 5.]]),
indices=tensor([[3, 2, 1],
[3, 2, 1]]))

第1维上最小的3个数从小到大的值与其所对应的索引：

a.topk(3,dim=1,largest=False) 

torch.return_types.topk(
values=tensor([[0., 1., 2.],
[4., 5., 6.]]),
indices=tensor([[0, 1, 2],
[0, 1, 2]]))

第k小的值 .kthvalue()

第1维上第4小的值，也就是最大的值：

a.kthvalue(4,dim=1)  

torch.return_types.kthvalue(
values=tensor([3., 7.]),
indices=tensor([3, 3]))

第3小的值，也就是第二大的值：

a.kthvalue(3)        

torch.return_types.kthvalue(
values=tensor([2., 6.]),
indices=tensor([2, 2]))

第1维上第2小的值，也就是最3大的值：

a.kthvalue(2,dim=1) 

torch.return_types.kthvalue(
values=tensor([1., 5.]),
indices=tensor([1, 1]))

5、compare

a>0,a.dtype

(tensor([[False, True, True, True],
[ True, True, True, True]]),
torch.float32)

gt为great,同上，表示>0：

torch.gt(a,0)  

tensor([[False, True, True, True],
[ True, True, True, True]])

a != 0

tensor([[False, True, True, True],
[ True, True, True, True]])

b = torch.ones(2,3)
c = torch.randn(2,3)
b,c

(tensor([[1., 1., 1.],
[1., 1., 1.]]),
tensor([[-0.2182, -0.7458, -0.4226],
[-0.0562, -1.0081, 0.9595]]))

①torch.eq(a,b)

a与b中各个元素是否相等，返回由bool值组成的list

torch.eq(b,c)

tensor([[False, False, False],
[False, False, False]])

②torch.eaqul(a,b)

a与b整体是否相等，返回一个bool值

torch.equal(b,b)

True

十二、高阶操作

1、where根据条件选取源头,可以替换不方便的循环逻辑控制

    torch.where(condition,源头x，源头y）→tensor

返回：

return a tensor of elements selected from either x or y,depending on condition:
if condition,out_i = x_i,
otherwise,out_i = y_i

cond = torch.tensor([[0.6769,0.7271],[0.8884,0.4163]])
cond

tensor([[0.6769, 0.7271],
[0.8884, 0.4163]])

a = torch.full([2,2],0.)
a

tensor([[0., 0.],
[0., 0.]])

b = torch.full([2,2],1.)
b

tensor([[1., 1.],
[1., 1.]])

torch.where(cond>0.5,a,b)

tensor([[0., 0.],
[0., 1.]])

#retrieve global label
prob = torch.randn(4,10)
prob

tensor([[ 2.5846, 0.1205, 0.9951, -0.3636, 0.3576, 1.6804, -0.4364, -0.7844,
0.4014, 0.1721],
[ 3.4028, -0.1766, -0.7051, 1.3496, -0.8652, -1.1937, -0.0648, -1.0526,
-0.8368, -0.2342],
[-1.9581, 1.1129, 1.2058, -1.0913, 1.5528, 0.6695, 1.0291, 1.4307,
-1.2577, -0.7917],
[-0.2095, 0.6609, -0.7099, 0.6236, -1.5831, 0.6597, 1.2883, -1.1838,
-0.4961, -0.6793]])

idx = prob.topk(dim=1,k=3)
idx

torch.return_types.topk(
values=tensor([[ 2.5846, 1.6804, 0.9951],
[ 3.4028, 1.3496, -0.0648],
[ 1.5528, 1.4307, 1.2058],
[ 1.2883, 0.6609, 0.6597]]),
indices=tensor([[0, 5, 2],
[0, 3, 6],
[4, 7, 2],
[6, 1, 5]]))

idx = idx[1]
idx

tensor([[0, 5, 2],
[0, 3, 6],
[4, 7, 2],
[6, 1, 5]])

label = torch.arange(10)+100
label

tensor([100, 101, 102, 103, 104, 105, 106, 107, 108, 109])

2、gather查表

torch.gather(input,dim,index,out=None)→tensor
gather values along an axis specified by dim.
for a 3-D tensor the output is specified by out[i][j][k]=input[i][j][index[i][j][k]] #if dim == 2

torch.gather(label.expand(4,10),dim=1,index=idx.long())#输入，维度，表格
#5 0 6分别对应105,100,106

tensor([[100, 105, 102],
[100, 103, 106],
[104, 107, 102],
[106, 101, 105]])

十三、认识深度学习

预测未来：根据历史数据学习出某种规律，并依赖这些规律实现预测。

数学家们将能够根据历史数据实现预测或得出某种结果的计算步骤或计算方法称之为算法。

算法是数学方法，计算机进行规模化计算。

1、神经网络

模拟人脑结构，复现人脑思考规律、以制造和人相似的智慧为目的的算法——人工神经网咯（Artificial neural network，ANN）：

圆表示神经元（包含激活函数，任何基于感知机的算法都必须要存在一个激活函数，确定激活函数是神经网络的计算核心），
线模拟“轴突”（ 线性关系z(由参数和输入的数据共同决定) ）
数据就是电信号。每个输入的特征都匹配一个权重（输入向量的维度与输入神经元的个数相同）

1950年“图灵测试”被提出，1956年“人工智能”、“机器学习”（使用机器实现算法）概念被提出。
人工神经网络最初只能解决线性问题、对数据需求量大、计算时间长、无法达到人类智力水平。
同时期逻辑回归、KNN、决策树等算法概念逐渐被发明出来，机器学习中的其他算法开始繁荣发展，而神经网络却无人问津。
十年之后，其他机器学习算法的性能遇到了瓶颈，到2000年，神经网络算法有了长足的进步，全球数据量激增，芯片、云技术迅猛发展，人类获得了前所未有的巨大算力。

神经网络非常复杂，是一个黑箱算法。神经网络是深度学习中最复杂的算法，但是原理不难。调参很难，因为它不可解释。

为神经网络的相关研究取一个单独的名字：深度学习（属于机器学习，以研究人工神经网络为核心的）。

人工智能 > 机器学习 > 深度学习

2、认识pytorch框架与库

（1）框架(framework)

pytorch是torch库的python版本。
一个神经网络如何才是优秀的呢？（1）加大数据规模（2）调整神经网络的架构。
一个优秀的深度学习框架，必须具备非常高的灵活性和可调试性，才能不断推进深度学习算法的研究。

pytorch是为高速运行巨量数据的神经网络而生，pytorch既保证了神经网络结果优秀，又衡量了计算速度。
pytorch支持研究环境和生产环境的无缝切换，调试成本很低。
pytorch一直遵守“简单胜于复杂”的原则，继承了python的语法风格。学术界用pytorch比较广，工业界用tensorflow比较多。
在以后的工业界中，pytorch应用会越来越多。

（2）库（library）：

两大模块的层次是并列的，当导入库的时候，这样做：

import torch
import torchvision 

实际上对pytorch进行安装时，同时安装了torch和torchvision等模块。

当需要优化算法时，运行：

from torch import optim

十四、梯度

导数derivate
偏微分partial derivate
梯度gradient #把所有的偏微分看成向量

凸函数像碗一样

鞍点：在一个点处取到一个维度的极小值，另一个维度的极大值

影响因素：

initialization初始状态（初始位置）
learning rate lr学习率（可以先调成0.001）
escape minima 逃出局部最小值：添加动量（惯性）

梯度▽=（y对w的偏微分，y对b的偏微分）

1、激活函数

根据青蛙实验，借鉴生物神经元的生物机制，发现：
神经网络的输出结果并不是各个输入的简单求和，而是有一个阈值响应机制。
只有满足激活函数条件的值有输出结果。

机器学习中可用的激活函数只有六种：恒等函数、阶跃函数sign、sigmoid、tanh、ReLU、softmax。

softmax、恒等函数几乎不会出现在隐藏层上
sign、tanh几乎不会出现在输出层上
ReLU、sigmoid在隐藏层和输出层上应用广泛
激活函数(如果在中间层上，用h(z)表示；如果在输出层上，用g(z)表示）

.

h(z)：激活函数一般指的是隐藏层上的，隐藏层的激活函数变动会影响输出结果。同一层上的激活函数应该保持一致，方便调试（也可以设置不同）
g(z)：输出层上的激活函数对输出结果无影响

（1）为了解决阶梯函数不可导的情况，科学家提出了连续的激活函数：sigmoid:

f(x) = 1/(1+e^(-x))
·可导，对x的导数=f(x)-f²(x)=f(x)(1-f(x))，导数在0点最大
·值域(0,1)
·缺点：当x越来越大，导数逐渐趋近于0，导数=f(x)，就会出现函数长期得不到更新的现象，即梯度弥散（梯度消失）

·实际中，变量之间的关系通常都不是一条直线，而是呈现出某种曲线关系。为了让统计模型更好地拟合曲线，统计学家在线性回归方程的两边引入了联系函数(link function)，对线性回归方程做各种变化，将变化后的方程称为“广义线性回归”。such as 等式两边同时取对数的对数函数回归；同时取指数的S形函数回归等。在这一过程中，统计学家注意到sigmoid函数带来的变化：
·sigmoid 可以化连续性变量为分类型变量（比如设置阈值为0.5，当σ>0.5时为1，σ<0.5时为0）
·将结果以几率（σ/(1-σ)）的形式呈现，即可得出线性回归的z：ln（σ/(1-σ)）=Xw。因为这个性质，在等号两边加sigmoid的算法被称为“对数几率回归”，在英文中就是logistic regression逻辑回归。逻辑回归是广义线性回归中最广为人知的算法，它是一个叫做“回归”（自变量是线性）实际上总是被用来做分类的算法。【σ是事件发生的概率，1-σ是事件不会发生的概率，σ/(1-σ)就是样本被预测为1的相对概率。当样本对应的σ越接近1或0，则认为逻辑回归对这个样本的预测结果越肯定，样本被分类正确的可能性也越高；如果σ非常接近阈值，就说明逻辑回归对这个样本究竟是哪个类别，不是非常肯定。】

z = torch.linspace(-100,100,10)
z

tensor([-100.0000, -77.7778, -55.5556, -33.3333, -11.1111, 11.1111,
33.3333, 55.5556, 77.7778, 100.0000])

torch.sigmoid(z)#把值变为（0,1）

tensor([0.0000e+00, 1.6655e-34, 7.4564e-25, 3.3382e-15, 1.4945e-05, 9.9999e-01,
1.0000e+00, 1.0000e+00, 1.0000e+00, 1.0000e+00])

（2）tanh 英文发音/tai chi/

·=2*sigmoid(2x)-1
·多用于RNN中
·值域（-1,1）
·中心点（0,0），自变量为0时导数最大

a = torch.linspace(-1,1,10)
a

tensor([-1.0000, -0.7778, -0.5556, -0.3333, -0.1111, 0.1111, 0.3333, 0.5556,
0.7778, 1.0000])

torch.tanh(a)#值域（-1,1）

tensor([-0.7616, -0.6514, -0.5047, -0.3215, -0.1107, 0.1107, 0.3215, 0.5047,
0.6514, 0.7616])

（3）ReLU(Rectified Linear Unit)推荐优先使用，是神经网络领域中的宠儿 英文发音：/rel-you/

0,z<0 不响应，导函数为0
z,z>0 响应，导函数为1，不会放大和缩小，不会出现梯度弥散和梯度爆炸的现象
·可以用于清除负元素
·导函数是阶跃函数

a

tensor([-1.0000, -0.7778, -0.5556, -0.3333, -0.1111, 0.1111, 0.3333, 0.5556,
0.7778, 1.0000])

torch.relu(a)

tensor([0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.1111, 0.3333, 0.5556, 0.7778,
1.0000])

（4）Leaky ReLU

x<0 , y = ax (a很小,一般为0.02)

x>0 , y = x

#使用方法很简单,在原来ReLU的地方换成LeakyReLU
self.model = nn.Sequential(
    nn.Linear(784,200),
    nn.LeakyReLU(inplace = True)，
    nn.Linear(200,200),
    nn.LeakyReLU(inplace = True)，
    nn.Linear(200,10),
    nn.LeakyReLU(inplace = True)，
)

File “< ipython-input-150-8cfd5b39a69f>”, line 4
nn.LeakyReLU(inplace = True)，
^
SyntaxError: invalid character in identifier

（5）SELU：解决ReLU在0处不连续的问题

（6）softplus：把ReLU在0处做平滑处理

（7）sign符号函数（在0点两侧符号相反），也称阶跃函数 1,z>0； 0，z=0; -1,z<0 #很少用

X = torch.tensor([[1,0,0],[1,1,0],[1,0,1],[1,1,1]],dtype=torch.float32)
andgate = torch.tensor([[0],[0],[0],[1]],dtype=torch.float32) #andgate = x1&x2
w = torch.tensor([-0.2,0.15,0.15],dtype=torch.float32)

def LinearRwithsign(X,w):
    zhat = torch.mv(X,w)  
    andhat = torch.tensor([int(x) for x in zhat >= 0],dtype=torch.float32)    
    return zhat,andhat

zhat,andhat = LinearRwithsign(X,w)
zhat,andhat

(tensor([-0.2000, -0.0500, -0.0500, 0.1000]), tensor([0., 0., 0., 1.]))

十五、tipical loss

1、基本优化思想

模型训练的目标：令神经网络的输出结果与真实值尽量接近。
模型训练：
1）定义基本模型，明确目标是求解权重向量w
2）定义损失函数/目标函数 （评估真实值与预测值差异的函数，以权重向量为自变量）
·求解损失函数需要用到复杂的数学工具：
·将损失函数L(w)转变成凸函数的数学方法，常见的有拉格朗日变换
·在凸函数上求解L(w)的最小值对应的w的方法，也就是以梯度下降为代表的优化算法
对于回归类神经网络而言，最常见的损失函数是SSE=
3）定义优化算法
4）以最小化损失函数为目标，求解权重

2、损失函数：

（1）MSE【Mean squared error（均方误差）】:用于回归

reduction = “mean”

MSELoss = (1/m)∑(zi-zihat)² = (L2_norm)² = (1/m)*∑(y实际的值-yhat模型的输出值)²

（2）SSE【sum of the Squared Errors】：SSE = ∑(zi-zihat)²

reduction = “sum”

from torch.nn import MSELoss

yhat = torch.randn(size=(50,),dtype=torch.float32)
y = torch.randn(size=(50,),dtype=torch.float32)

类在使用之前一定要实例化。实例化要用criterion/loss：
如果想知道一个函数有没有参数，方法：把光标放到括号处，按shift+Tab：

criterion = MSELoss()

loss = criterion(yhat,y)#loss = criterion(真实值，预测值)
loss#均方误差MSE的值

tensor(1.9280)

criterion = MSELoss(reduction = "sum")

loss = criterion(yhat,y)#loss = criterion(真实值，预测值)
loss

tensor(96.4017)

（3）Cross Entropy Loss（交叉熵），也叫对数损失：用于分类。

熵表示“不确定性”

交叉熵H(p,q) = -∑p(x)logq(x)。
·当q越来越逼近于p时，H越来越接近0；
·当p=q，cross entropy值 = entropy值

·binary：二分类

极大似然估计求解：如果希望一件事发生，就应该增加这件事发生的概率，就只需要寻找其发生概率最大化的权重w。
步骤：
①构筑似然函数P(w)，用于评估目标事件发生的概率。该函数被设计成目标事件发生时，概率最大。
②对整体似然函数取对数，构成对数似然函数lnP(w)
③在对数似然函数上对权重w求导，并使导数为0，对权重进行求解

P(yihat|xi,w) = P1^yi * P0^(1-yi)，在数学上叫做逻辑回归的假设函数。yi表示样本的真实标签。这时模型的效果最好。
两边同时取ln，把连乘变成连加：lnP = ∑（yi*ln(σi） + (1-yi)*ln(1-σi))#σi指激活函数的输出结果
这就是二分类交叉熵损失函数。

求Loss希望求得极小值，而不是极大值。因此在前面加上“-”号：
L(w)i = -∑（yi*ln(σi） + (1-yi)*ln(1-σi)) #σi指激活函数的输出结果
只要求得最小值，就可以让模型在训练数据上拟合效果最好。具体求解需要用到优化算法。

·multi-class：多分类

深度学习基本都是：多分类交叉熵损失。
多分类的标签不再服从0-1分布。σ指softmax函数的输出结果。
交叉熵函数：L(w) = -∑yi_(k=j)ln(σi)。二分类交叉熵函数可以看成多分类交叉熵函数的一种特殊形式。
在求解时，取对数操作是在确定了似然函数后进行的，但从计算结果来看，对数操作只对softmax函数的结果σ起效。
因此在实际操作中，把ln(softmax(z))单独定义了一个功能：logsoftmax，pytorch中可以直接通过nn.logsoftmax类调用这个功能。
同时，把对数之外的，乘以标签、加和、取负等过程打包起来，称为负对数似然函数（Negitive Log Likelihood function）， 在pytorch中用nn.NLLLoss来进行调用。

·+softmax：与softmax激活函数搭配使用

·softmax对张量进行放缩，每个值都是（0,1），且所有值加起来=1
·把数值转化成概率[2.0,1.0,0.1]→[0.7,0.2,0.1]，把原来大的值放得更大，把原来小的压缩到比较密集的空间。原来2是1的两倍，经过变化，0.7是0.2的3.5倍。
·leave it to logistic regression part

为什么对于分类问题不使用MSE？

sigmoid+MSE：会出现梯度消失的问题
交叉熵收敛速度更快
注：如果用交叉熵效果不好，可以使用MSE

#Loss = -(y*ln(sigma) + (1-y)*ln(1-sigma))
#y - 真实标签
#sigma二分类的预测概率 - sigmoid(z)
#z = Xw X是特征张量，w是权重
#X,w
#m 样本量

m = 3*pow(10,3)  #科学记数法3000
torch.random.manual_seed(420)
X = torch.rand((m,4),dtype=torch.float32)
w = torch.rand((4,1),dtype=torch.float32)
y = torch.randint(low=0,high=2,size=(m,1),dtype=torch.float32)#[0,2)，所以取值是0,1.有几个样本就有几个标签

zhat = torch.mm(X,w)#metrix*metrix
sigma = torch.sigmoid(zhat)
sigma.shape

torch.Size([3000, 1])

loss = -(1/m)*sum(y*torch.log(sigma) + (1-y)*torch.log(1-sigma))  #(total loss)/m
loss

tensor([0.7962])

m = 3*pow(10,6)
torch.random.manual_seed(420)
X = torch.rand((m,4),dtype=torch.float32)#X.shape:[3000000,4]
w = torch.rand((4,1),dtype=torch.float32)
y = torch.randint(low=0,high=2,size=(m,1),dtype=torch.float32)#[0,2)，所以取值是0,1.有几个样本就有几个标签
zhat = torch.mm(X,w)#metrix*metrix
sigma = torch.sigmoid(zhat)

import time#观察两种方法：sum / torch.sum  运算的时间
start1 = time.time()#捕获现在的时间,以秒计
loss1 = -(1/m)*    sum  (y*torch.log(sigma) + (1-y)*torch.log(1-sigma))
now1 = time.time()#捕获现在的时间，以秒计
print(now1 - start1)

18.511772871017456

start2 = time.time()#捕获现在的时间,以秒计
loss2 = -(1/m)*torch.sum(y*torch.log(sigma) + (1-y)*torch.log(1-sigma))#只要不是简单的数字加减，就一定要用torch当中的函数：torch.
now2 = time.time()#捕获现在的时间，以秒计
print(now2 - start2)

0.03202319145202637

"""
由于交叉熵损失太常用了，因此在pytorch里面有专门的类用于计算，这里介绍两个nn模块中的类：
class BCEWithLogitsLoss
    内置了sigmoid函数与交叉熵函数，它会自动计算输入值的sigmoid值。因此需要输入zhat与真实标签，且顺序不能变化，zhat必须在前。

class BCELoss
    只有交叉熵函数，没有sigmoid层。因此需要输入sigma与真实标签，且顺序不能变化
    
这两个类都要求预测值与真实标签的数据类型（必须是浮点型）以及结构（shape）必须相同，否则运行就会报错。

"""
import torch.nn as nn
criterion1 = nn.BCELoss()#实例化   BCELoss(reduction="mean"得到平均值 / "sum"得到加和结果 / "none"得到矩阵)
loss1 = criterion1(sigma,y)

criterion2 = nn.BCEWithLogitsLoss()#实例化
loss2 = criterion2(zhat,y)  #与BCELoss输入不同。精度比BCELoss高。

loss1,loss2#可以看到结果相同

(tensor(0.8685), tensor(0.8685))

"""
深度学习基本都是：多分类交叉熵损失
LogSoftmax + Negtive Log Likelihood function
"""
import torch
import torch.nn as nn
m = 3*pow(10,3)
torch.random.manual_seed(420)
X = torch.rand((m,4),dtype=torch.float32)#X.shape:[3000000,4]
w = torch.rand((4,3),dtype=torch.float32)
y = torch.randint(low=0,high=3,size=(m,),dtype=torch.float32)#[0,3)，所以取值是0,1.有几个样本就有几个标签
zhat = torch.mm(X,w)#metrix*metrix

#logsoftmax - log + softmax，输入：zhat
#MLLLoss()
logsm = nn.LogSoftmax(dim=1)#实例化
logsigma = logsm(zhat)
logsigma

tensor([[-1.1139, -0.8802, -1.3585],
[-1.0558, -0.8982, -1.4075],
[-1.0920, -1.0626, -1.1430],
…,
[-1.0519, -0.9180, -1.3805],
[-1.0945, -1.1219, -1.0798],
[-1.0276, -0.8891, -1.4649]])

criterion = nn.NLLLoss()#计算损失
criterion(logsigma,y.long())#y需要是整型，不能是浮点型。因为交叉熵损失需要将标签转化为one-hot，因此不接受浮点数作为标签的输入

tensor(1.1147)

"""
更简便的方法：直接调用CrossEntropyLoss
    criterion = nn.CrossEntropyLoss()
    criterion(zhat,y.long())#只需要输入zhat
"""
criterion = nn.CrossEntropyLoss()
criterion(zhat,y.long())#只需要输入zhat

tensor(1.1147)

重视展示网络结构和灵活性，应该使用不包含输出层激活函数的类：
通常在Model类中，__init__中层的数量与forward函数中对应的激活函数的数量是一致的。如果使用内置sigmoid/logsoftmax功能的类来计算损失函数，
forward函数在定义时就会少一层(输出层)，网络结构展示就不够简单明了。
对于结构复杂的网络而言，结构清晰就更为重要。
同时，如果激活函数是单独写的，要修改激活函数就变得很容易。如果混在损失函数中，要修改激活函数时就得改掉整个损失函数的代码，不利于维护。

重视稳定性和运算精度，使用包含输出层激活函数的类：
如果在一个Model中， 很长时间都不修改输出层的激活函数，考虑到模型的稳定运行，就使用内置了激活函数的类来计算损失函数。
同时，内置激活函数可以帮助推升运算的精度。

‘\n重视展示网络结构和灵活性，应该使用不包含输出层激活函数的类：\n通常在Model类中，__init__中层的数量与forward函数中对应的激活函数的数量是一致的。如果使用内置sigmoid/logsoftmax功能的类来计算损失函数，\nforward函数在定义时就会少一层(输出层)，网络结构展示就不够简单明了。\n对于结构复杂的网络而言，结构清晰就更为重要。\n同时，如果激活函数是单独写的，要修改激活函数就变得很容易。如果混在损失函数中，要修改激活函数时就得改掉整个损失函数的代码，不利于维护。\n\n重视稳定性和运算精度，使用包含输出层激活函数的类：\n如果在一个Model中， 很长时间都不修改输出层的激活函数，考虑到模型的稳定运行，就使用内置了激活函数的类来计算损失函数。\n同时，内置激活函数可以帮助推升运算的精度。\n\n’

如何使用pytorch自动求导：

方法一：torch.autograd.grad(loss,[w1,w2,…])
[w1 grad,w2 grad…]

方法二：loss.backward()
调用方法：
w1.grad
w2.grad

1、熵：信息量之和，信息量越大，熵越大，事件越确定，越没有惊喜感

a = torch.full([4],1/4.)
a

tensor([0.2500, 0.2500, 0.2500, 0.2500])

-(a*torch.log2(a)).sum()

tensor(2.)

a = torch.tensor([0.1,0.1,0.1,0.7])
-(a*torch.log2(a)).sum()

tensor(1.3568)

a = torch.tensor([0.001,0.001,0.001,0.999])
-(a*torch.log2(a)).sum()                  

tensor(0.0313)

#数据稳定
from torch.nn import functional as F
x = torch.randn(1,784)
w = torch.randn(10,784)
logits = x@w.t()
pred = F.softmax(logits,dim=1)  
pred_log = torch.log(pred)
F.cross_entropy(logits,torch.tensor([3]))  #cross_tropy里的第一个参数必须是logits

tensor(16.1506)

F.nll_loss(pred_log,torch.tensor([3])) #cross_entropy = softmax + log + nll_loss

tensor(16.1506)

2、多分类：把 softmax 放于输出层之前。

·在多分类中，神经元的个数与标签的个数是一致的。例如：如果是十分类，在输出层上就会存在十个神经元，分别输出十个不同的概率。此时样本的预测标签就是所有输出的概率中最大的概率对应的标签类别。

·softmax分子是多分类状况下 某一个 标签类别的回归结果的指数函数
分母是多分类状况下 所有 标签类别的回归结果的指数函数之和
softmax函数的结果代表了样本的结果为类别k的概率
例如：有三个分类：苹果，梨，百香果。样本i被分类为百香果的概率为：σ百香果 = e_z百香果 / (e_z苹果 + e_z梨 + e_z百香果)

from torch.nn import functional as F
x = torch.ones(1)
w = torch.full([1],2.)
mse = F.mse_loss(torch.ones(1),x*w) #(predict,label)
x,w,mse

(tensor([1.]), tensor([2.]), tensor(1.))

torch.autograd.grad(mse,[w]) #w在初始化时没有设置为需要导数信息，因此这里默认w不需要求导

---------------------------------------------------------------------------

RuntimeError                              Traceback (most recent call last)

 in 
----> 1 torch.autograd.grad(mse,[w]) #w在初始化时没有设置为需要导数信息，因此这里默认w不需要求导


D:\anaconda\lib\site-packages\torch\autograd\__init__.py in grad(outputs, inputs, grad_outputs, retain_graph, create_graph, only_inputs, allow_unused)
    200         retain_graph = create_graph
    201 
--> 202     return Variable._execution_engine.run_backward(
    203         outputs, grad_outputs_, retain_graph, create_graph,
    204         inputs, allow_unused)


RuntimeError: element 0 of tensors does not require grad and does not have a grad_fn

w.requires_grad_()#必须是浮点数。对w信息进行更新，告诉pytorch w需要求导

tensor([2.], requires_grad=True)

torch.autograd.grad(mse,[w])#这里报错的原因是w是动态图，也就是做一步更新一步。这里的图还是原来的图

---------------------------------------------------------------------------

RuntimeError                              Traceback (most recent call last)

 in 
----> 1 torch.autograd.grad(mse,[w])#这里报错的原因是w是动态图，也就是做一步更新一步。这里的图还是原来的图


D:\anaconda\lib\site-packages\torch\autograd\__init__.py in grad(outputs, inputs, grad_outputs, retain_graph, create_graph, only_inputs, allow_unused)
    200         retain_graph = create_graph
    201 
--> 202     return Variable._execution_engine.run_backward(
    203         outputs, grad_outputs_, retain_graph, create_graph,
    204         inputs, allow_unused)


RuntimeError: element 0 of tensors does not require grad and does not have a grad_fn

mse = F.mse_loss(torch.ones(1),x*w)#更新
torch.autograd.grad(mse,[w])#求loss对w的偏导

(tensor([2.]),)

求偏导的另一种方法：backward。在完成前向传播的过程中，pytorch会记录下来所有的路径。因此在最后的loss节点上从后往前传播：

mse = F.mse_loss(torch.ones(1),x*w)#更新
mse.backward()
w.grad   #不能多次运行

tensor([2.])

import torch 
from torch.nn import functional as F
#softmax
a = torch.rand(3)
a.requires_grad_()

tensor([0.0983, 0.3098, 0.4726], requires_grad=True)

p = F.softmax(a,dim=0)#在feature维度上进行操作
p

tensor([0.2710, 0.3349, 0.3941], grad_fn=)

requires_grad=True只适用一次，第二次运行的时候就已经被清除掉了，需要重新设置：

p.backward() 

---------------------------------------------------------------------------

RuntimeError                              Traceback (most recent call last)

 in 
----> 1 p.backward() # requires_grad=True只适用一次，第二次运行的时候就已经被清除掉了，需要重新设置


D:\anaconda\lib\site-packages\torch\tensor.py in backward(self, gradient, retain_graph, create_graph)
    219                 retain_graph=retain_graph,
    220                 create_graph=create_graph)
--> 221         torch.autograd.backward(self, gradient, retain_graph, create_graph)
    222 
    223     def register_hook(self, hook):


D:\anaconda\lib\site-packages\torch\autograd\__init__.py in backward(tensors, grad_tensors, retain_graph, create_graph, grad_variables)
    124 
    125     grad_tensors_ = _tensor_or_tensors_to_tuple(grad_tensors, len(tensors))
--> 126     grad_tensors_ = _make_grads(tensors, grad_tensors_)
    127     if retain_graph is None:
    128         retain_graph = create_graph


D:\anaconda\lib\site-packages\torch\autograd\__init__.py in _make_grads(outputs, grads)
     48             if out.requires_grad:
     49                 if out.numel() != 1:
---> 50                     raise RuntimeError("grad can be implicitly created only for scalar outputs")
     51                 new_grads.append(torch.ones_like(out, memory_format=torch.preserve_format))
     52             else:


RuntimeError: grad can be implicitly created only for scalar outputs

p = F.softmax(a,dim=0)
torch.autograd.grad(p[1],[a],retain_graph=True)  #i与j相等时梯度为正，其余为负。i是1,所以[0,1,2]中只有索引1对应的值是正的

(tensor([-0.0908, 0.2227, -0.1320]),)

torch.autograd.grad(p[2],[a])

(tensor([-0.1068, -0.1320, 0.2388]),)

（2）softmax溢出现象

由于softmax的分母和分子中都带有以e为底的指数函数，所以在计算中非常容易出现极大的数值。如果数字超出计算机处理室要求的有限数据宽度，计算机无法运算和表示，这种现象叫做“溢出”。

z = torch.tensor([1010,100,999],dtype=torch.float32)
torch.exp(z)/torch.sum(torch.exp(z))#数据发生了溢出

tensor([nan, nan, nan])

torch.softmax(z,0)       #没有溢出
#softmax只能对单一维度的数据进行计算。所以即使输入的是一维的，也需要指定softmax运算时的维度索引，否则就会报错
#从输出结果来看，1010的概率最大。输入值最大，输出结果也最大。
#所以如果不需要知道具体的输出概率，可以不用softmax就可以从 输入数值 直接看出 输出结果

tensor([9.9998e-01, 0.0000e+00, 1.6701e-05])

z = torch.tensor([10,9,5],dtype=torch.float32)
torch.exp(z)/torch.sum(torch.exp(z))

tensor([0.7275, 0.2676, 0.0049])

torch.softmax(z,0)

tensor([0.7275, 0.2676, 0.0049])

torch.softmax(z,0).sum() #概率之和为1

tensor(1.)

注：关于softmax( , )的维度参数

s = torch.tensor([[[1,2,4,5],[3,4,4,5],[5,6,4,5]],[[5,6,4,5],[7,8,4,5],[9,10,4,5]]],dtype=torch.float32)
s,s.shape

#表示一个tensor有两个二维表，每个表有三行，每行有四个元素

(tensor([[[ 1., 2., 4., 5.],
[ 3., 4., 4., 5.],
[ 5., 6., 4., 5.]],
[[ 5., 6., 4., 5.],
[ 7., 8., 4., 5.],
[ 9., 10., 4., 5.]]]),
torch.Size([2, 3, 4]))

正向索引：

s.shape[0],s.shape[1],s.shape[2]

(2, 3, 4)

负向索引：

s.shape[-3],s.shape[-2],s.shape[-1]

(2, 3, 4)

每张二维表概率之和为1：

torch.softmax(s,dim=0)

tensor([[[0.0180, 0.0180, 0.5000, 0.5000],
[0.0180, 0.0180, 0.5000, 0.5000],
[0.0180, 0.0180, 0.5000, 0.5000]],
[[0.9820, 0.9820, 0.5000, 0.5000],
[0.9820, 0.9820, 0.5000, 0.5000],
[0.9820, 0.9820, 0.5000, 0.5000]]])

每张表上，每列上各元素之和为1：

torch.softmax(s,dim=1)

tensor([[[0.0159, 0.0159, 0.3333, 0.3333],
         [0.1173, 0.1173, 0.3333, 0.3333],
         [0.8668, 0.8668, 0.3333, 0.3333]],

        [[0.0159, 0.0159, 0.3333, 0.3333],
         [0.1173, 0.1173, 0.3333, 0.3333],
         [0.8668, 0.8668, 0.3333, 0.3333]]])

每张表上，每行上各元素之和为1：

torch.softmax(s,dim=2)

tensor([[[0.0128, 0.0347, 0.2562, 0.6964],
         [0.0723, 0.1966, 0.1966, 0.5344],
         [0.1966, 0.5344, 0.0723, 0.1966]],

        [[0.1966, 0.5344, 0.0723, 0.1966],
         [0.2562, 0.6964, 0.0128, 0.0347],
         [0.2671, 0.7262, 0.0018, 0.0049]]])

3、使用cross_entropy进行多分类实战

w1,b1 = torch.randn(200,784,requires_grad = True),torch.zeros(200,requires_grad = True) #torch.randn(ch-out,ch-in)
w2,b2 = torch.randn(200,200,requires_grad = True),torch.zeros(200,requires_grad = True)
w3,b3 = torch.randn(10,200,requires_grad = True),torch.zeros(10,requires_grad = True)  #十分类，所以输出是10

def forward(x):
    x = x@w1.t() + b1  #x 点乘 权重1 + 偏置1
    x = F.relu(x)      #经过激活函数relu
    x = x@w2.t() + b2  #x 点乘 权重2 + 偏置2
    x = F.relu(x)      #经过激活函数relu
    x = x@w3.t() + b3  #x 点乘 权重3 + 偏置3
    x = F.relu(x)      #经过激活函数relu      把没有经过softmax/sigmoid的叫logits。这一步也可以不经过relu，直接输出
    return x

import torch
from torch import nn
from torch import optim

epochs = 10
optimizer = optim.SGD([w1,b1,w1,b2,w3,b3],lr = 1e-3) #优化器
criteon = nn.CrossEntropyLoss()

for epoch in range(epochs):
    for batch_idx,(data,target) in enumerate(train_loader):
        data = data.view(-1,28*28)
        
        logits = forward(data)  #不要再加softmax
        loss = criteon(logits,target)
        
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()

4、二分类神经网络的原理及实现

（1）tensor实现二分类神经网络的正向传播

import torch

X = torch.tensor([[1,0,0],[1,1,0],[1,0,1],[1,1,1]],dtype=torch.float32)
X

#第一列代表常量神经元，第二列代表x1，第二列代表x2

tensor([[1., 0., 0.],
[1., 1., 0.],
[1., 0., 1.],
[1., 1., 1.]])

andgate = x1&x2：

andgate = torch.tensor([[0],[0],[0],[1]],dtype=torch.float32) 

def LogisticR(X,w):#def LogisticR
    w = torch.tensor([-0.2,0.15,0.15],dtype=torch.float32)
    zhat = torch.mv(X,w)
    sigma = 1/(1 + torch.exp(-zhat))  #sigmoid的自变量用sigma定义  #也可以写成sigma = torch.sigmoid(zhat)
    andhat = torch.tensor([int(x) for x in sigma >= 0.5],dtype=torch.float32)  #人为设置阈值,大于阈值的标签为1，小于阈值的标签为0
    #在python中，int(True)=1，int(Flase)=0。直接放入列表推导式，把布尔值转化为0和1
    return sigma,andhat

sigma,andhat = LogisticR(X,w)
sigma,andhat

(tensor([0.4502, 0.4875, 0.4875, 0.5250]), tensor([0., 0., 0., 1.]))

andgate  #andhat与andgate结果一样    记住:所有加hat的都是预测值

tensor([0., 0., 0., 1.])

画图

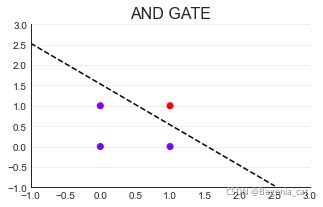
(1)AND GATE

import matplotlib.pyplot as plt
import seaborn as sns
X = torch.tensor([[1,0,0],[1,1,0],[1,0,1],[1,1,1]],dtype=torch.float32)
#设置一个画布
plt.figure(figsize=(5,3))#设置画布大小
plt.scatter(X[:,1],X[:,2]#取X索引为1的列为x，取X索引为2的列为y
           ,c=andgate    #andgate有0,1两种取值。颜色=真实标签的类别
           ,cmap="rainbow"#使用彩虹色中对比度比较高的两种颜色
           )#绘制散点图
#美化图片
plt.style.use('seaborn-whitegrid')#设置图像的风格
sns.set_style("white")
plt.title("AND GATE",fontsize=16)#设置图像标题
plt.xlim(-1,3)                   #设置横坐标尺寸
plt.ylim(-1,3)                   #设置纵坐标尺寸
plt.grid(alpha=.4,axis="y")      #显示背景中的网格
plt.gca().spines["top"].set_alpha(.0)#让上方的坐标轴被隐藏
plt.gca().spines["right"].set_alpha(.0)#让右侧的坐标轴被隐藏
#画决策边界
import numpy as np
x = np.arange(-1,3,0.5)#(-1,3)有规律排列的数据
plt.plot(x,(0.23-0.15*x)/0.15
        ,color="k",linestyle="--");

二维平面中，任意一条线可以被表示为x1 = ax2 + b
变换一下，0 = b - x1 + ax2
         0 = [1 - x1 + x2] * [b,-1,a].T
         0 = Xw 
X是特征张量，w是权重向量（默认为列向量）
    当w,b固定时，直线就是固定的。
    当w,b不固定时，直线就是任意一条直线。
    
在直线上方的点为0类（z <= 0），在直线下方的点为1类（z > 0）#可以用阶跃函数实现
具有分类功能的线叫做决策边界

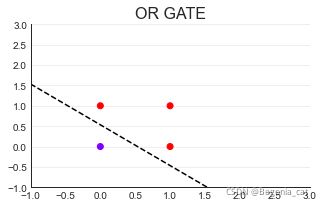
(2)OR GATE

import torch
X = torch.tensor([[1,0,0],[1,1,0],[1,0,1],[1,1,1]],dtype=torch.float32)
orgate = torch.tensor([0,1,1,1],dtype=torch.float32)
def OR(X):
    w = torch.torch.tensor([-0.08,0.15,0.15],dtype=torch.float32)
    zhat = torch.mv(X,w)
    yhat = torch.tensor([int(x) for x in zhat >= 0.5],dtype=torch.float32)
    return orgate
import matplotlib.pyplot as plt
import seaborn as sns
#设置一个画布
plt.figure(figsize=(5,3))#设置画布大小
plt.scatter(X[:,1],X[:,2]#取X索引为1的列为x，取X索引为2的列为y
           ,c=orgate    #andgate有0,1两种取值。颜色=真实标签的类别
           ,cmap="rainbow"#使用彩虹色中对比度比较高的两种颜色
           )#绘制散点图
#美化图片
plt.style.use('seaborn-whitegrid')#设置图像的风格
sns.set_style("white")
plt.title("OR GATE",fontsize=16)#设置图像标题
plt.xlim(-1,3)                   #设置横坐标尺寸
plt.ylim(-1,3)                   #设置纵坐标尺寸
plt.grid(alpha=.4,axis="y")      #显示背景中的网格
plt.gca().spines["top"].set_alpha(.0)#让上方的坐标轴被隐藏
plt.gca().spines["right"].set_alpha(.0)#让右侧的坐标轴被隐藏
#画决策边界
import numpy as np
x = np.arange(-1,3,0.5)#(-1,3)有规律排列的数据
plt.plot(x,(0.08-0.15*x)/0.15
        ,color="k",linestyle="--");

(3)NAND GATE

import torch
X = torch.tensor([[1,0,0],[1,1,0],[1,0,1],[1,1,1]],dtype=torch.float32)
nandgate = torch.tensor([1,1,1,0],dtype=torch.float32)
def NAND(X):
    w = torch.torch.tensor([0.23,-0.15,-0.15],dtype=torch.float32)
    zhat = torch.mv(X,w)
    yhat = torch.tensor([int(x) for x in zhat >= 0],dtype=torch.float32)
    return nandgate

import matplotlib.pyplot as plt
import seaborn as sns
#设置一个画布
plt.figure(figsize=(5,3))#设置画布大小
plt.scatter(X[:,1],X[:,2]#取X索引为1的列为x，取X索引为2的列为y
           ,c=nandgate    #andgate有0,1两种取值。颜色=真实标签的类别
           ,cmap="rainbow"#使用彩虹色中对比度比较高的两种颜色
           )#绘制散点图
#美化图片
plt.style.use('seaborn-whitegrid')#设置图像的风格
sns.set_style("white")
plt.title("NAND GATE",fontsize=16)#设置图像标题
plt.xlim(-1,3)                   #设置横坐标尺寸
plt.ylim(-1,3)                   #设置纵坐标尺寸
plt.grid(alpha=.4,axis="y")      #显示背景中的网格
plt.gca().spines["top"].set_alpha(.0)#让上方的坐标轴被隐藏
plt.gca().spines["right"].set_alpha(.0)#让右侧的坐标轴被隐藏
#画决策边界
import numpy as np
x = np.arange(-1,3,0.5)#(-1,3)有规律排列的数据
plt.plot(x,(0.23-0.15*x)/0.15
        ,color="k",linestyle="--");

import torch
X = torch.tensor([[1,0,0],[1,1,0],[1,0,1],[1,1,1]],dtype=torch.float32)
xorgate = torch.tensor([0,1,1,0],dtype=torch.float32)

import matplotlib.pyplot as plt
import seaborn as sns
#设置一个画布
plt.figure(figsize=(5,3))#设置画布大小
plt.scatter(X[:,1],X[:,2]#取X索引为1的列为x，取X索引为2的列为y
           ,c=xorgate    #andgate有0,1两种取值。颜色=真实标签的类别
           ,cmap="rainbow"#使用彩虹色中对比度比较高的两种颜色
           )#绘制散点图
#美化图片
plt.title("XOR GATE",fontsize=16)#设置图像标题
plt.xlim(-1,3)                   #设置横坐标尺寸
plt.ylim(-1,3)                   #设置纵坐标尺寸
plt.grid(alpha=.4,axis="y")      #显示背景中的网格
plt.gca().spines["top"].set_alpha(.0)#让上方的坐标轴被隐藏
plt.gca().spines["right"].set_alpha(.0)#让右侧的坐标轴被隐藏

sigma_nand = NAND(X)#返回nandgate
sigma_nand

tensor([1., 1., 1., 0.])

sigma_or = OR(X)#返回orgate
sigma_or

tensor([0., 1., 1., 1.])

x0 = torch.tensor([1,1,1,1],dtype=torch.float32)
x0

tensor([1., 1., 1., 1.])

input_2 = torch.cat((x0.view(4,1),sigma_nand.view(4,1),sigma_or.view(4,1)),dim=1)#合并tensor,拼接的内容要用()或[]框起来   
input_2

#用dim指定方向，dim=0，三个张量横向拼接为tensor([1., 1., 1., 1., 0., 1., 1., 1., 0., 1., 1., 1.])；
#dim=1，三个张量按列排开
#因为x0,sigma_nand,sigma_or都是一维张量，没有dim=1的维度。所以需要把三个张量都变成二维的：用view变成指定的样子。

tensor([[1., 1., 0.],
[1., 1., 1.],
[1., 1., 1.],
[1., 0., 1.]])

import torch
X = torch.tensor([[1,0,0],[1,1,0],[1,0,1],[1,1,1]],dtype=torch.float32)
andgate = torch.tensor([0,0,0,1],dtype=torch.float32)
def AND(X):
    w = torch.torch.tensor([-0.2,0.15,0.15],dtype=torch.float32)
    zhat = torch.mv(X,w)
    andhat = torch.tensor([int(x) for x in zhat >= 0],dtype=torch.float32)
    return andhat

AND(input_2)

tensor([0., 1., 1., 0.])

#所有非线性的问题都必须用多层神经网络实现

5、GPU加速

device = torch.device('cuda:0')
net = MLP().to(device)
optimizer = optim.SGD([net.parameters()],lr = learning_rate) #优化器
criteon = nn.CrossEntropyLoss().to(device)

for epoch in range(epochs):
    for batch_idx,(data,target) in enumerate(train_loader):
        data = data.view(-1,28*28)
        data,target = data.to(device),target.cuda()   #.to(device)与.cuda() 等效，区别是.to(device)是CPU搬到GPU；.cuda()只能指定GPU，

十六、链式法则

前向传播：求导之前要先向右计算一次所有的变量值

1、单层感知机：

（1）单层（只有1层输出的）线性回归神经网络

（特征输入） 输入信号 > 人工神经元 > 信号输出 （预测结果输出）

神经网络的层数不包括“输入层”

zhat(z的预测结果) = wi * xi + b。用矩阵表示：zhat = Xw(x中为1的那一列是专门用来和权重相乘的)
为什么是z不是y？在深度学习中，y永远表示标签。因为深度学习的输出不是标签，所以不用y。通常用粗体的小写字母表示列向量，粗体的大写字母表示矩阵或行列式。在机器学习中，默认所有的一维向量都是列向量。

线性回归的任务：拟合。
预测函数的本质是需要构建的模型，预测函数的核心是找出模型的参数向量w
把竖着排列的称为一层，一个神经元上只有一个特征，神经元的个数=特征数+1（1指偏差对应的神经元）。输出层至少有一个神经元。连接的线称为轴突，

x = torch.randn(1,10)                        #输入
w = torch.randn(1,10,requires_grad = True)  #权重，w维度为1
o = torch.sigmoid(x@w.t())                  #激活函数（输入@权重）
o.shape

torch.Size([1, 1])

loss = F.mse_loss(torch.ones(1,1),o)
loss.shape

torch.Size([])

loss.backward()

w.grad

tensor([[-0.1313, 0.0248, 0.0298, -0.0075, -0.0821, 0.0185, 0.0354, 0.0332,
-0.0105, 0.0642]])

例：算出z的结果。z=b + w1x1 + w2x2

import torch
#对于pytorch，很多情况都要求进行运算的两个参数类型一致
#建议定义tensor时一定要定义数据类型。而且如果不要求整数时，一律设置为float类型，且设置为float32（32比64节省内存）。如果报错再进行调整。
X = torch.tensor([[1,0,0],[1,1,0],[1,0,1],[1,1,1]]
                 ,dtype = torch.float32)
#也可以写成这样变成浮点型：
#X = torch.tensor([[1,0,0],[1,1,0],[1,0,1],[1,1,1]]）
#X.float()
w = torch.tensor([-0.2,0.15,0.15]) #(b,w1,w2)b在最前面,可以根据矩阵为1的那一列（权重所对应的列）的位置，更改偏置和权重的位置
X,w

(tensor([[1., 0., 0.],
[1., 1., 0.],
[1., 0., 1.],
[1., 1., 1.]]),
tensor([-0.2000, 0.1500, 0.1500]))

def LinearR(X,w):   #冒号“:”别忘记       R表示Regression
    zhat = torch.mv(X,w)#mv是矩阵*向量专用的函数MatrixVector
    return zhat

zhat = LinearR(X,w)   #Linear参数必须类型相同
zhat#预测值

tensor([-0.2000, -0.0500, -0.0500, 0.1000])

torch.Tensor([[1,0,0],[1,1,0],[1,0,1],[1,1,1]])#Tensor生成的是浮点数

tensor([[1., 0., 0.],
[1., 1., 0.],
[1., 0., 1.],
[1., 1., 1.]])

tensor与Tensor的区别：

torch.tensor会先判断输入的数据类型，然后根据其确定tensor中的数据类型
torch.Tensor无论输入数据是什么，都会无脑输出float32

z = torch.tensor([-0.2000, -0.0500, -0.0500,  0.1000])#真实值
z.ndim  #维度

1

zhat == z #这里的“不等”一定不是数据类型的原因。

tensor([ True, False, False, False])

#SSE = SIGMA（（真实值-预测值）*2）
zhat-z

tensor([0.0000e+00, 3.7253e-09, 3.7253e-09, 7.4506e-09])

SSE = sum((zhat - z)**2)
SSE#从SSE可以看出，zhat和z确实不等

tensor(8.3267e-17)

torch.set_printoptions(precision=30)#打印选项：打印小数点后30位

zhat,z
#不相等的原因：
#float32由于只保留32位，所以精确度有问题
#torch.mv函数在计算时，内部会存在很微小的问题

(tensor([[0.695239484310150146484375000000],
         [0.566381037235260009765625000000],
         [1.094140648841857910156250000000],
         [0.965282201766967773437500000000]], grad_fn=),
 tensor([-0.200000002980232238769531250000, -0.050000000745058059692382812500,
         -0.050000000745058059692382812500,  0.100000001490116119384765625000]))

preds = torch.ones(300,68,64,64)
preds.shape

torch.Size([300, 68, 64, 64])

a = 300*68*64*64
a#共有多少数据

83558400

preds = torch.ones(300,68,64,64) * 0.1
preds.sum() * 10   #发现 *0.1 和 *10 带来了精度问题。

#所以如果结果的精确度要求高，就需要在创建时设置float64精度。注意float64只能减小，不能消除精度问题。

tensor(83558328.)

preds = torch.ones(300,68,64,64)
preds.sum()

tensor(83558400.)

torch.allclose(zhat,z)#.allclose()可以帮助无视很小的区别(可以手动设置阈值)，来比较两个张量是否一致

True

（2）torch.nn.Linear（表示输出层，是nn.modual大类下的子类）实现单层回归神经网络的正向传播

torch.nn.Linear(上一层的神经元中 给现在这一层传输的神经元个数，这一层接受上一层传输数据的神经元的个数, bias = 默认为True)。
#如果不需要bias，则写output = torch.nn.Linear(2,1，bias = False)。这个时候output.bias什么都不返回。

使用时不需要定义w,b。

输入层由特征矩阵决定，所以在神经网络中不需要定义输入层，所以看一个网络有几层时，不算输入层。

用这种方法生成的z只是和 特征矩阵 结构相似的随机数，还没有告诉神经网络去预测正确结果

torch.set_printoptions(precision=4)#调整打印选项：打印小数点后4位

X = torch.tensor([[0,0],[1,0],[0,1],[1,1]],dtype=torch.float32)
X#X不需要专门留出一列1给偏差

tensor([[0., 0.],
[1., 0.],
[0., 1.],
[1., 1.]])

#实例化nn.Linear。会自动随机生成w,b
output = torch.nn.Linear(2,1) 

zhat = output(X)
zhat

tensor([[ 0.1788],
[-0.0734],
[ 0.1401],
[-0.1121]], grad_fn=)

output.weight,output.bias#查看自动随机生成的w,b

(Parameter containing:
tensor([[-0.2522, -0.0387]], requires_grad=True),
Parameter containing:
tensor([0.1788], requires_grad=True))

#如果不想让w,b随机，就设置“随机数种子”：在系统的很多组w,b中固定选择一种。数字自己随便设置，每个数字对应一种模式，具体对应哪种模式计算机也不是很清楚，我们只需要锁住它就行。这里设置为420号。

torch.random.manual_seed(420)#人为设置随机数种子。

output = torch.nn.Linear(2,1)
zhat = output(X)
zhat,zhat.shape#用这种方法生成的z只是和 特征矩阵 结构相似的随机数，还没有告诉神经网络去预测正确结果

(tensor([[0.6730],
[1.1048],
[0.2473],
[0.6792]], grad_fn=),
torch.Size([4, 1]))

（3）torch.functional实现单层二分类神经网络的正向传播 => 也就是逻辑回归

逻辑回归与线性回归唯一的区别就是：在线性回归的结果之后套上了sigmoid函数

只要让nn.Linear输出结果再经过sigmoid函数，就可以实现逻辑回归的正向传播了。

#在nn.module里调出来的都是类，在nn.functional里调出来的全是函数

import torch
from torch.nn import functional as F  #把函数简写为F，这样就可以直接F.去调用函数，如：F.sigmoid()
X = torch.tensor([[0,0],[1,0],[0,1],[1,1]],dtype=torch.float32)
torch.random.manual_seed(420)
dense = torch.nn.Linear(2,1)#实例化torch
zhat = dense(X) #dense意为“紧密”，表示上一层大部分神经网络都与这一层紧密相连，表示全连接层
sigma = F.sigmoid(zhat)
y = [int(x) for x in sigma >= 0.5]
y#由于w,b是随机生成的，所以y只需要看格式，内容不需要关注是否与andgate结果相同

[1, 1, 1, 1]

sign：

zhat,torch.sign(zhat) #z>0全部返回1

(tensor([[0.6730],
[1.1048],
[0.2473],
[0.6792]], grad_fn=),
tensor([[1.],
[1.],
[1.],
[1.]], grad_fn=))

ReLU

F.relu(zhat)#>0返回原值，<0返回0

tensor([[0.6730],
[1.1048],
[0.2473],
[0.6792]], grad_fn=)

tanh

torch.tanh(zhat)#zhat>0，所以返回结果全部位于(0,1)

tensor([[0.5869],
[0.8022],
[0.2424],
[0.5910]], grad_fn=)

2、多层感知机：

x = torch.randn(1,10)
w = torch.randn(2,10,requires_grad = True)
o = torch.sigmoid(x@w.t())
o.shape

torch.Size([1, 2])

loss = F.mse_loss(torch.ones(1,2),o)
loss

tensor(0.5097, grad_fn=)

loss.backward()
w.grad

tensor([[ 0.0167, 0.0093, 0.0218, -0.0144, 0.0156, -0.0078, -0.0311, -0.0236, 0.0132, 0.0180],
[ 0.0020, 0.0011, 0.0026, -0.0017, 0.0019, -0.0009, -0.0037, -0.0028, 0.0016, 0.0022]])

w.grad.shape

torch.Size([2, 10])

神经网络是黑箱

从左往右的过程是神经网络的正向传播过程。左边的层叫“上层”，右边的层叫“下层”。输入是第0层，第一个隐藏层称为第一层。

神经元从上往下编号，1,2，……。

不同神经元的区别在于加和之后使用的激活函数(如果在中间层上，用h(z)表示；如果在输出层上，用g(z)表示）。z是加和的结果，σ是加和之后所经过激活函数之后的结果。
z和σ位于神经元上，w和b位于层之间连接处。

神经网络非常复杂，要弄清楚每个w,b是不可能的。
所以深度学习不太看重可解释性，因为我们是不知道神经网络是怎么做的。要想从最后的结果追溯到输入的特征是非常困难的。

单层神经网络的w是一个列向量，但是在多层神经网络中，W是矩阵，因为有多层，多组w取值。
Z要和特征标签顺序一致。为了让Z保持列向量，所以需要把W写在X前面，也就是列行，n_featuresn_samples

真正让神经网络拥有处理线性和非线性问题的能力的，是隐藏层上的激活函数。如果没有激活函数，输出结果就
只是做了仿射变换，依然是线性变换，不能解决非线性问题。可见，“层”本身不是解决神经网络的非线性问题的关键，
层上的h(z)才是。如果h(z)是线性函数或者不存在，那增加再多的层也没用。

可以尝试把上述AND,OR,NAND的激活函数注释掉，或换成另一个激活函数，观察输出结果。

从0实现深度神经网络的正向传播：

"""
题目：假设有500条数据，20个特征，标签分为3分类。
现在要实现一个三层神经网络：第一层有13个神经元，第二层有8个神经元，第三层是输出层。
其中第一层的激活函数是relu，第二层的激活函数是sigmoid。
实现代码如下：
"""
import torch
import torch.nn as nn
from torch.nn import functional as F

#确定数据
torch.random.manual_seed(420)#锁定随机数种子
x = torch.rand((500,20),dtype=torch.float32)
y = torch.randint(low=0,high=3,size=(500,1),dtype=torch.float32)#randint随机生成整数(0,3]
#实例化nn.Linear的同时会自动生成w，所以不需要定义w

#继承nn.Model类完成正向传播  torch.nn -> nn.Model,nn.functional
class Model(nn.Module):#括号里输入想要继承的父类的名字
    def __init__(self,in_features=10,out_features=2):   
        """
    用于定义class Model这个类本身。nn.Module这个类有几千行代码，其中init函数代码就占了大多数。
    括号里第一个参数是固定不变的self，表示这个类本身。
    in_features表示输入该神经网络的特征数（输入层上的神经元数目），out_features表示该神经网络的输出的特征数（输出层上的神经元数目）。   
        """
    
        super(Model,self).__init__()
        """
    super帮助继承父类更多的细节。
    需要继承的子模块名称[查找Model的父类模块nn.Model，把nn.model中的__init__全部复制到子类的__init__中。]
    如果没有super这一行，子类就无法继承父类的init函数，下面神经网络的各个层也就不能定义了。
        """
        self.Linear1 = nn.Linear(in_features,13,bias=True) #(上层神经元数，下层神经元数)
        self.Linear2 = nn.Linear(13,8,bias=True)
        self.output = nn.Linear(8,out_features,bias=True)
    
    def forward(self,x):#神经网络向前传播
        #第一层
        z1 = self.Linear1(x)#线性层
        sigma1 = torch.relu(z1)#激活函数的输出结果
        #第二层
        z2 = self.Linear2(sigma1)#线性层加和结果
        sigma2 = torch.sigmoid(z2)#sigmoid的结果
        #输出层
        z3 = self.output(sigma2)
        sigma3 = F.softmax(z3,dim=1)#输出层上三个神经元，三个输出结果。计算softmax的第一维，得出三个类别的概率
        return sigma3

x.shape#x有20列，所以输入层上的神经元个数应该是20

torch.Size([500, 20])

x.shape[1],y.unique()#y中不重复的标签

(20, tensor([0., 1., 2.]))

input_ = x.shape[1]
output_ = len(y.unique())
input_,output_

(20, 3)

#实例化神经网络
torch.random.manual_seed(420)
net = Model(in_features=input_,out_features=output_)

net.forward(x).shape  #500行3列，500个样本，3个输出类别
#效果等同于net(x)。因为__init__下面只有一个函数，所以当输入net(x)之后，就会自动执行__init__下面所有定义的函数

torch.Size([500, 3])

net.Linear1.weight.shape#第一个线性层上的矩阵.shape    #x(500,20)

torch.Size([13, 20])

#w(13,20) * (20,500)先把特征矩阵转置 -> (13,500)

net.Linear2.weight.shape

torch.Size([8, 13])

#w(8,13) * (13,500) -> (8,500)

net.output.weight.shape

torch.Size([3, 8])

#w(3,8) * (8,500) ->(3,500)。softmax输出时再进行调换变为(500,3)

net.Linear1.bias.shape#从输入层进入到第一个隐藏层中，因为第一层有13个神经元，所以第一层的bias.shape是3

torch.Size([13])

super函数

#建立一个父类
class FooParent(object):
    def __init__(self):
        self.parent = 'PARENT!!'#属性
        print('Running __init__,I am parent')
    def bar(self,message):
        self.bar = "This is bar" 
        print("%s from Parent" % message)
FooParent()#父类实例化对瞬间，运行自己的__init__

Running __init__,I am parent





<__main__.FooParent at 0x1f35c5da6a0>

父类运行自己的__init__中定义的属性：

FooParent().parent

Running __init__,I am parent





'PARENT!!'

建立一个子类，并通过类名调用让子类继承父类的方法与属性：

class FooChild(FooParent):
    def __init__(self):
        print("Running __init__,I am child")
FooChild().bar("HAHAHA")#查看子类是否继承了方法

Running __init__,I am child
HAHAHA from Parent

#子类没有继承父类的__init__中定义的属性，只继承了__init__之外的函数：

FooChild().parent 

Running __init__,I am child



---------------------------------------------------------------------------

AttributeError                            Traceback (most recent call last)

 in 
----> 1 FooChild().parent #子类没有继承父类的__init__中定义的属性


AttributeError: 'FooChild' object has no attribute 'parent'

创建一个子类，并使用super函数：

class FooChild(FooParent):
    def __init__(self):
        super(FooChild,self).__init__()#如果希望子类继承父类的__init__中定义的属性，就需要使用super()
        #super这句的含义是：找到FooChild的父类，并继承__init__
        print("I am running __init__,I am child")
FooChild().parent#再次调用parent属性，执行子类的init功能的同时，也执行了父类的init函数定义的功能

Running __init__,I am parent
I am running __init__,I am child





'PARENT!!'

属性的继承

net.training#现在这个类是否用于训练？如果是，就返回True;否则返回False

True

"""
方法的继承
net.cuda()      #将整个网络转移到GPU上进行
net.cpu()       #将整个网络转移到CPU上进行
net.apply()     #对神经网络中所有的层，init函数中所有的对象都执行同样的操作
net.Linear1.weight.data.fill_(0)#一次性把tensor中所有的元素填成0
"""

def initial_0(m):#让w,b都为0
    print(m)
    if type(m) == nn.Linear:
        m.weight.data.fill_(0)
        print(m.weight)
net.apply(initial_0)

Linear(in_features=20, out_features=13, bias=True)
Parameter containing:
tensor([[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.]],
       requires_grad=True)
Linear(in_features=13, out_features=8, bias=True)
Parameter containing:
tensor([[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.]],
       requires_grad=True)
Linear(in_features=8, out_features=3, bias=True)
Parameter containing:
tensor([[0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0.]], requires_grad=True)
Model(
  (Linear1): Linear(in_features=20, out_features=13, bias=True)
  (Linear2): Linear(in_features=13, out_features=8, bias=True)
  (output): Linear(in_features=8, out_features=3, bias=True)
)





Model(
  (Linear1): Linear(in_features=20, out_features=13, bias=True)
  (Linear2): Linear(in_features=13, out_features=8, bias=True)
  (output): Linear(in_features=8, out_features=3, bias=True)
)

net.parameters()

for param in net.parameters():
    print(param)#打印，观察parameters迭代器，发现里面包含了所有的权重和截距。一定要掌握parameters。

Parameter containing:
tensor([[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.]],
       requires_grad=True)
Parameter containing:
tensor([ 1.3508e-01,  1.5439e-01, -1.9350e-01, -6.8777e-02,  1.3787e-01,
        -1.8474e-01,  1.2763e-01,  1.8031e-01,  9.5152e-02, -1.2660e-01,
         1.4317e-01, -1.4945e-01,  3.4258e-05], requires_grad=True)
Parameter containing:
tensor([[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.]],
       requires_grad=True)
Parameter containing:
tensor([ 0.0900, -0.0597,  0.0268, -0.0173,  0.0065,  0.0228, -0.1408,  0.1188],
       requires_grad=True)
Parameter containing:
tensor([[0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0.]], requires_grad=True)
Parameter containing:
tensor([-0.0156, -0.0730, -0.2637], requires_grad=True)

3、链式法则 :通过乘积完成对比较复杂的梯度的求解

ay/ax = (ay/au) * (au/ax)

x = torch.tensor(1.)
w1 = torch.tensor(2.,requires_grad = True)
b1 = torch.tensor(1.)
w2  = torch.tensor(2.,requires_grad = True)
b2 = torch.tensor(1.)
y1 = x*w1+b1
y2 = y1*w2+b2

dy2_dy1 = torch.autograd.grad(y2,[y1],retain_graph = True)[0]
dy1_dw1 = torch.autograd.grad(y1,[w1],retain_graph = True)[0]
dy2_dw1 = torch.autograd.grad(y2,[w1],retain_graph = True)[0]
dy2_dy1*dy1_dw1

tensor(2.)

dy2_dw1

tensor(2.)

十七、神经网络

1、梯度下降中的两个问题

在梯度下降最开始时，会先随机设定初始权重w(0)，对应的纵坐标L(w(0))就是初始的损失函数值，坐标点(w(0),L(w(0)))就是梯度下降的起始点。接着从起始点开始，让自变量w向损失函数L(w)减小最快的方向移动。起始点是一个“盲人”，没有上帝视角。它不知道全局，每次走都得用“拐杖”——梯度向量确定方向。每次走都只敢走一小段距离，每走一下都要重新确认方向。只有这样走很多步之后，才能够到达或接近损失函数的最小值。
每步的方向就是当前坐标点对应的梯度向量的反方向，每步的距离就是步长 * 当前坐标点所对应的梯度向量的大小（即梯度向量的模长）。

（1）怎么找出梯度的大小和方向？

梯度向量中的具体元素就是各个自变量的偏导数，这些偏导数的具体值必须依赖于当前所在的坐标点(w,loss)的值进行计算。
让坐标点动起来（进行一次迭代）：本质就是在原来坐标的基础上分别减去相应的值。
偏导数的大小影响整体梯度向量的大小，偏导数前的“-”号影响整体梯度向量的方向。

（2）怎么让坐标点按照梯度向量的反方向 移动与梯度向量大小相等的距离？

2、MLP(multi-layer perceptron)反向传播

找出距离和方向：反向传播算法（又叫Delta法则）。1986年提出，利用链式法则成功实现了复杂网络求导过程的简单化。

反向传播的定义与价值：从左往右，从输出到输入，逐渐往前求解倒数的表达式，并且所使用的的节点上的张量，也是从后往前逐渐用到，这与正向传播的过程完全相反。这种从左到右，不断使用正向传播中的元素对梯度向量进行计算的方式称为反向传播。

pytorch可以帮我们自动计算梯度，我们只需要提取梯度向量的值就行。学习率一般是0.02~0.5。

pytorch可以帮我们自动计算梯度，我们只需要提取梯度向量的值就行。

import torch

x = torch.tensor(1,requires_grad = True,dtype = torch.float32)#requires_grad = True表示允许求
z = x**2

sigma = torch.sigmoid(z)

loss = -(y*torch.log(sigma)+(1-y)*torch.log(1-sigma))

torch.autograd.grad(loss,x)
"""
#如果已经进行过一次反向传播，pytorch会已经生成计算图。
当下一次正向传播时，pytorch会把计算图释放掉。
#所以需要再一次进行反向传播
"""

(tensor(-2.5379),)

"""
3分类(high)，500个样本，20个特征，共3层(一共四层，输入层不需要写)。第一层13个神经元，第二层8个神经元。
第一层激活函数是relu，第二层激活函数是sigmoid
神经元的个数与输入数据的特征数量相同
"""
import torch
import torch.nn as nn
from torch.nn import functional as F

#确定数据
torch.manual_seed(420)#生成随机数
x = torch.rand((500,20),dtype = torch.float32)
y = torch.randint(low = 0,high = 3,size = (500,),dtype = torch.float32) #定义成一维的
x

tensor([[0.8054, 0.1990, 0.9759, …, 0.0117, 0.2572, 0.2272],
[0.6076, 0.9066, 0.5540, …, 0.8121, 0.0603, 0.7086],
[0.0708, 0.5807, 0.8304, …, 0.8998, 0.0322, 0.4390],
…,
[0.7986, 0.6708, 0.7298, …, 0.1268, 0.1310, 0.8556],
[0.6634, 0.8943, 0.9527, …, 0.2029, 0.3998, 0.2302],
[0.7081, 0.1069, 0.1263, …, 0.0153, 0.4722, 0.0718]])

input_ = x.shape[1]
output_ = len(y.unique())

#定义神经网络的架构
#Logsoftmax+NLLLoss/CrossEntropyLoss
class Model(nn.Module):
    def __init__(self,in_features = 40,out_features = 2):
        super().__init__()
        self.linear1 = nn.Linear(in_features,13,bias = False)
        self.linear2 = nn.Linear(13,8,bias = False)
        self.output = nn.Linear(8,out_features,bias = True)
        
    def forward(self,x):
        sigma1 = torch.relu(self.linear1(x))
        sigma2 = torch.sigmoid(self.linear2(sigma1))
        zhat = self.output(sigma2)
        return zhat

#实例化
torch.manual_seed(420)
net = Model(in_features = input_,out_features = output_)

zhat = net.forward(x)

#定义损失函数
criterion = nn.CrossEntropyLoss()

loss = criterion(zhat,y.long())#只接受整型的y
loss

tensor(1.1535, grad_fn=)

net.linear1.weight#梯度与权重相对应

Parameter containing:
tensor([[ 1.3656e-01, -1.3459e-01, …省略…]],
requires_grad=True)

net.linear1.weight.grad

tensor([[ 2.2618e-05, 5.5898e-06, …省略…]])

loss.backward()
"""
反向传播,不能重复计算
如果想要重复计算，必须把正向传播重新执行一次，并执行loss.backward(retain_graph = True)保留计算图
因此如果想多次运行，需要在代码里写上保留计算图  retain_graph = True
"""

net.linear1.weight.grad.shape

torch.Size([13, 20])

net.linear1.weight.shape

torch.Size([13, 20])

在进行正向传播时，权重是自动生成的，同时自动设置了requires_grad = True,所以不需要手动设置。

叶子结点：右侧没有节点的节点。backward会识别叶子结点，不在叶子上的变量是不会被backward所考虑的。只有backward = True的节点才会被计算，
在backward计算时，只会计算关于w的部分。如果w是自己设置的，一定要记得设置backward = True。

#w(t+1) = w(t) - 步长 * grad
lr = 10.0#learning rate,一般为0.001,0.01,0.05。
w = net.linear1.weight.data#现有的权重，w(t)
dw = net.linear1.weight.grad#梯度
w = w - lr * dw
w

tensor([[ 0.1363, -0.1346, …省略…]])

普通梯度下降过程：正向传播、计算梯度、更新权重。

但是这个过程非常缓慢，尤其是当学习率非常小的时候，看不到w的变化。

（1）加速迭代的方法：动量法momentum

之前我们说过，在梯度下降过程中，起始点是一个“盲人”， 它看不到也听不到全局，所以每次移动都要重新评算计算方向与距离，并且每次只能走一小步。 但不只限于此，起始点不仅看不到前面的路，也无法从过去走的路中学习。
想象一下，我们被蒙上眼睛，由另一个人喊口号来给与我们方向让我们移动，假设喊口号的人一-直喊:”向前，向前，向前。“因为我们看不见，在最初的三四次，我们可能都只会向前走一小步， 但如果他一直让我们向前，我们就会失去耐心，转而向前走一大步， 因为我们可以预测:前面很长-段路大概都是需要向前的。对梯度下降来说，也是同样的道理如果在很长段时间内，起始点一直向相似的方向移动，那按照步长小步-小步地磨着向前是没有意义的，既浪费计算资源又浪费时间，此时就应该大但地照着这个方向走-大步。相对的，如果我们很长时间都走向同一个方向，突然让我们转向，那我们转向的第一步就应该非常谨慎，走-小步。
不难发现，真正高效的方法是:在历史方向与现有方向相同的情况下，迈出大步子；在历史方向与现有方向相反的情况下，迈出小步子。那要怎么才能让起始点了解过去的方向呢?我们让上一步的梯度向量(的反方向)与现在这一点的梯度向量(的反方向)以加权的方式求和，求解出受到上一步大小和方向影响的真实下降方向，再让坐标点向真实下降方向移动。在坐标轴上，可以表示为:
对上一步的梯度向量加上的权重被称为动量参数（也叫衰减力度，通常使用γ表示），对这一点的梯度向量加上的权重就是步长（依然表示为η），真实移动的向量为v，被称为“动量”（Momentum）
v(t) = γv(t-1) - η*(L/αw)
w(t+1) = w(t) + v(t)
在第一步中，没有历史梯度方向，因此第一步的真实方向就是起始点梯度的反方向，v0=0.其中v(t-1)代表了之前所有步骤所积累的动量和（即上一步的真实方向）。在这种情况下，梯度下降的方向就有了“惯性”，受到历史累计动量的影响，当新坐标点的梯度反方向与历史累计动量的方向一致时，历史累计动量会加大实际方向的步子；相反，当新坐标点的梯度反方向与历史累计动量的方向不一致时，历史累计动量会减小实际方向的步子。

#momentum
lr = 0.1
gamma = 0.9#每次都按照上一步的0.9计算真实的方向v(t)
dw = net.linear1.weight.grad
w = net.linear1.weight.data
dw.shape,net

(torch.Size([13, 20]),
Model(
(linear1): Linear(in_features=20, out_features=13, bias=False)
(linear2): Linear(in_features=13, out_features=8, bias=False)
(output): Linear(in_features=8, out_features=3, bias=True)
))

"""
t=1,走第一步进行首次迭代的时候，需要一个v0
v是历史方向。第一步是没有方向的，所以定义为0
"""
v = torch.zeros(dw.shape[0],dw.shape[1])

#v(t) = gamma*v(t-1) - lr +dv
#w(t+1) = w(t) +v(t)

v = gamma *v - lr * dw
w += v#在普通梯度下降中是w -= v，在这里是+=
w

tensor([[ 0.1364, -0.1346, …省略…]])

（2）torch.optim实现带动量的梯度下降

（1）确定数据
（2）定义神经网络的架构
（3）定义损失函数
（4）定义优化算法

#导入库
import torch
import torch.nn as nn
from torch.nn import functional as F
import torch.optim as optim

#确定数据,超参数
torch.manual_seed(420)#生成随机数
x = torch.rand((500,20),dtype = torch.float32)*100
y = torch.randint(low = 0,high = 3,size = (500,),dtype = torch.float32) #定义成一维的
lr = 0.1
gamma = 0.9

#定义神经网络的架构
#Logsoftmax+NLLLoss/CrossEntropyLoss
class Model(nn.Module):
    def __init__(self,in_features = 40,out_features = 2):
        super().__init__()
        self.linear1 = nn.Linear(in_features,13,bias = False)
        self.linear2 = nn.Linear(13,8,bias = False)
        self.output = nn.Linear(8,out_features,bias = True)
        
    def forward(self,x):
        sigma1 = torch.relu(self.linear1(x))
        sigma2 = torch.sigmoid(self.linear2(sigma1))
        zhat = self.output(sigma2)
        return zhat

#类Model需要输入的参数
input_ = x.shape[1]        #特征的数目
output_ = len(y.unique())  #分类的数目

#实例化神经网络类，让神经网络准备好正向传播
torch.manual_seed(420)
net = Model(in_features = input_,out_features = output_)

#定义损失函数
criterion = nn.CrossEntropyLoss()

#定义优化算法  使用小批量随机梯度下降
opt = optim.SGD(net.parameters()  #需要进行迭代的权重
                ,lr = lr
                ,momentum = gamma
                )
"""
#net.parameters()一次性到处现有神经网络架构下全部的权重和架构
#for x in net.parameters():
#    print(x)
"""

梯度下降流程：

（1）向前传播
（2）计算本轮向前传播的损失函数值
（3）反向传播 - 得到梯度
（4）更新权重（和动量）
（5）清空梯度。清除原来计算出来的基于上一个点的坐标计算出来的梯度，腾出计算和运行的空间。

#向前传播
zhat = net.forward(x)#zhat是最后一个线性层的输出结果。当时softmax结构时，神经网络的最后一层可以不写softmax函数。
#计算损失函数
loss = criterion(zhat,y.reshape(500).long())
#反向传播
loss.backward()
#更新权重
opt.step()#step代表步子，更新权重w，更新动量v
#清空梯度
opt.zero_grad()

print(loss)#不断运行，Loss会不断减小
print(net.linear1.weight.data[0][:10])

tensor(1.0918, grad_fn=)
tensor([ 0.1389, -0.1340, 0.2157, -0.1773, -0.0672, -0.1536, 0.1751, 0.0859,
-0.1108, -0.1726])

（3）开始迭代：batch_size与epochs

①为什么要有小批量？

小批量随机梯度下降是深度学习入门级的优化算法(梯度下降是入门级之下的) ,其求解与迭代流程与传统梯度下降(GD)基本一致，不过二者在迭代权重时使用的数据这一点上存在巨大的不同。传统梯度下降在每次进行权重迭代(即循环)时都使用全部数据，每次迭代所使用的数据也都一致。而mini- batch SGD是每次迭代前都会从整体采样一批固定数目的样本组成批次(batch) B,并用B中的样本进行梯度计算，以减少样本量。
为什么会选择mini- batch SGD作为神经网络的入门级优化算法呢?有两个比较主流的原因。
①第一个是，比起传统梯度下降，mini-batch SGD更可能找到全局最小值。
·梯度下降是通过最小化损失函数来找对应参数向量的优化算法。对于任意损失函数L(w)而言，如果L(w)在其他点上的值比在w上的值更小，那么L(w)很可能就是一个局部最小值 (local minimum)。如果L(w)在w上的值是目标函数在整个定义域上的最小值，那么L(w)就是全局最小值(global minimum)。一个最容易理解的描述是，如果把地球海拔看作是一个函数，那世界上的许多海沟和盆地都是当地海拔最低的地区，他们就是一个个局部最小值.相对的，世界上最深的马里亚纳海沟就是海拔这个函数上的全局最小值，因为全世界没有比它更深的海底了。
·传统梯度下降是每次迭代时都会使用全部数据的梯度下降，所以每次使用的数据是一致的，因此梯度向量的方向和大小都只受权重w的影响，所以梯度方向的变化相对较小，很多时候看起来梯度甚至是指向一个方向(如上图所示)。这样带来的优势是可以使用较大的步长，快速迭代直到找到最小值。但是缺点也很明显，由于梯度方向不容易发生巨大变化，所以一旦在迭代过程中落入局部最优的范围，传统梯度下降就很难跳出局部最优，再去寻找全局最优解了。
而mini- batch SGD在每次迭代前都会随机抽取一批数效据， 所以每次迭代时带入梯度向量表达式的数据是不同的，梯度的方向同时受到系数w, b和带入的训练数据的影响，因此每次迭代时梯度向量的方向都会发生较大变化。并且，当抽样的数据量越小，本次迭代中使用的样本数据与上一次迭代中使用的样本数据之间的差异就可能越大，这也导致本次迭代中梯度的方向与上一次迭代中梯度的方向有巨大差异。所以对于mini-batchSGD而言，它的梯度下降路线看起来往往是曲折的折线(如上图所示）
极端情况下，当我们每次随机选取的批量中只有一个样本时，梯度下降的迭代轨迹就会变得异常不稳定(如上图所示)。我们称这样的梯度下降为随机梯度下降(stochastic gradient descent, SGD)。
mini batch SGD的优势是算法不会轻易陷入局部最优，由于每次梯度向量的方向都会发生巨大变化，因此- -旦有机会，算法就能够跳出局部最优走向全局最优(当然也有可能是跳出一个局部最优，走向另一个局部最优)。不过缺点是，需要的迭代次数变得不明。如果最开始就在全局最优的范围内，那可能只需要非常少的迭代次数就收敛，但是如果最开始落入了局部最优的范围，或全局最优与局部最优的差异很小，那可能需要花很长的时间、经过很多次迭代才能够收敛华意 不断改变的方向会让迭代的路线变得曲折。
从整体来看，为了mini- batch SGD这“不会轻易被局部最优困住的优点，我们在神经网络中使用它作为优化算法(或优化算法的基础)。当然，还有另一个流传更广、更为认知的理由支持我们使用mini batch SGD:mini-batch SGD可以提升神经网络的计算效率，让神经网络计算更快。
为了解决计算开销大的问题，我们要使用mini-batc GD。 考虑到可以从全部数据中选出一部分作为全部数据的近似估计”，然后用选出的这一部分数据来进行迭代，每次迭代需要计算的数据量就会更少，计算消耗也会更少，因此神经网络的速度会提升。当然了,这并不是说使用1001个样本进行迭代一定比使用1000个样本进行迭代速度要慢， 而是指每次迭代中计算上十万级别的数据，会比迭代中只计算一千个数据慢得多。

④batch size与epoches

在mini-batch SGD中，我们选择的批量batch含有的样本数被称为batch_ size（批量尺寸），这个尺寸一定是小于数据量的某个正整数值。每次迭代之前，我们需要从数据集中抽取batch_size个数据用于训练。
在普通梯度下降中，因为没有抽样，所以每次迭代就会将所有数据都使用一次，迭代了t次时，算法就将数据学习了t次。可以想象，对同样的数据，算法学习得越多，也有应当对数据的状况理解得越深，也就学得越好。然而，并不是对一个数据学习越多越好，毕竟学习得越多，训练时间就越长.同时，我们能够收集到的数据只是样本并不能够代表真实世界的客观情况。例如，我们从几万张猫与狗的照到的内容并不一定就能适用于全世界所有的猫和狗。如果我们的照片中猫咪都是有毛的，那神经网络对数据学习的程度越深，它就越有可能认不出无毛猫。因此，虽然我们希望算法对数据了解很深，但我们也希望算法不要变成"书呆子“，要保留一些灵活性(保留一些泛化能力)。关于这一-点，我们之后会详细展开来说明，但大家现在需要知道的是，算法对同样的数据进行学习的次数并不是越多越好。
在mini-batch SGD中，因为每次迭代时都只使用了一小部分数据，所以它迭代的次数并不能代表全体数据一共被学习了多少次。所以我们需要另一个重要概念：epoch,来定义全体数据一共被学习了多少次。

epoch：epoch是衡量训练数据使用次数的单位，一个epoch表示优化算法将全部训练数据都使用了一次，它与梯度下降中的迭代次数有非常深的关系。我们常常使用“完成1个epoch需要n次迭代”这样的语言。
假设一个数据集总共有m个样本，我们选择的batch_ size是N_B,即每次迭代时都使用N_B个样本，则一个epoch所需的迭代次数的计算公式如下:
完成一个epoch所需要的迭代次数n = m / N_B
在深度学习中，我们常常定义num_epoches作为梯度下降的最外层循环，batch_ size作为内层循环。有时候，希望数据被多学习几次，来增加模型对数据的理解。有时候，我们会控制模型对数据的训练。总之，我们会使用epoch和batch_ size来控制训练的节奏。接下来，我们就用代码来实现一下。
#epoch = 60 表示请让神经网络学习60次数据
for epochs in range(epoch):
for batch in range(batch):#请对每一个批量进行迭代
3.TensorDataset和DataLoader

import torch
from torch.utils.data import TensorDataset#用来打包数据，把特征和标签打包到一起
a = torch.randn(500,2,3)    #三维数据：（可以看成）二维表格
b = torch.randn(500,3,4,5)  #四维数据：图像数据
c = torch.randn(500,1)      #二维数据：标签
#被合并对象的第一维数据必须相等
for x in TensorDataset(b,c):#generator  按照第一维打包
    print(x)#得出特征张量和它所对应的标签
    break

(tensor([[[ 0.0806, 1.1339, 0.1410, 0.3593, 2.1796],
[-0.4336, -0.1106, 1.1228, -0.1804, 0.5361],
[-1.9375, 0.1241, -0.7275, 0.2676, 0.0118],
[-0.0511, -1.2384, -0.8405, 1.7962, -0.1198]],
[[ 0.0668, -2.1133, 1.1230, -0.1673, -0.3379],
[-2.5914, 1.0405, 1.4233, -1.0173, -0.7230],
[-0.6828, -0.9335, 0.5513, 0.1482, 0.4623],
[ 0.1665, -1.3033, 0.2815, 0.6613, 1.7401]],
[[-1.8565, 0.8329, 1.5913, 1.3783, 0.3283],
[ 0.3167, -1.4811, 1.4318, 1.7190, 0.9861],
[-0.5317, 1.2923, -1.2840, 0.2158, -0.0643],
[ 0.8721, 0.3452, -0.6808, -0.9248, -1.0642]]]), tensor([0.0547]))

from torch.utils.data import DataLoader#用来切割小批量的类

data = TensorDataset(b,c)
for x in DataLoader(data):#把数据放进来，不做处理
    print(x)
    break

[tensor([[[[ 0.0806, 1.1339, 0.1410, 0.3593, 2.1796],
[-0.4336, -0.1106, 1.1228, -0.1804, 0.5361],
[-1.9375, 0.1241, -0.7275, 0.2676, 0.0118],
[-0.0511, -1.2384, -0.8405, 1.7962, -0.1198]],
[[ 0.0668, -2.1133, 1.1230, -0.1673, -0.3379],
[-2.5914, 1.0405, 1.4233, -1.0173, -0.7230],
[-0.6828, -0.9335, 0.5513, 0.1482, 0.4623],
[ 0.1665, -1.3033, 0.2815, 0.6613, 1.7401]],
[[-1.8565, 0.8329, 1.5913, 1.3783, 0.3283],
[ 0.3167, -1.4811, 1.4318, 1.7190, 0.9861],
[-0.5317, 1.2923, -1.2840, 0.2158, -0.0643],
[ 0.8721, 0.3452, -0.6808, -0.9248, -1.0642]]]]), tensor([[0.0547]])]

bs=120   #例如定义batch_size=120
dataset = DataLoader(data
           ,batch_size = bs
           ,shuffle = True  #True表示抽样时要不要打乱数据
           ,drop_last = False
"""
#要舍弃最后一个batch吗？
当样本量无法除尽batch_size时，前面的小批量都取到了完整的batch，最后一个是不完整的。
一般选择False，不舍弃。
"""
           )
for i in dataset:
    print(i)

[tensor([[[[ 0.6777, -0.0586, …省略…

for i in dataset:
    print(i[0].shape)#可以看到分成了5个批次，最后一个批次被保留了

torch.Size([120, 3, 4, 5])
torch.Size([120, 3, 4, 5])
torch.Size([120, 3, 4, 5])
torch.Size([120, 3, 4, 5])
torch.Size([20, 3, 4, 5])

bs=120   #例如定义batch_size=120
dataset = DataLoader(data
           ,batch_size = bs
           ,shuffle = True  #True表示抽样时要不要打乱数据
           ,drop_last = True#True意为舍弃
           )
for i in dataset:
    print(i[0].shape)#分成的批次，最后一个批次被舍弃了

torch.Size([120, 3, 4, 5])
torch.Size([120, 3, 4, 5])
torch.Size([120, 3, 4, 5])
torch.Size([120, 3, 4, 5])

len(dataset)#一共有多少个batch

4

dataset.dataset#展示里面全部的数据

len(dataset.dataset)#总共有多少个样本

500

dataset.dataset[0]#其中的一个样本

(tensor([[[ 0.0806, 1.1339, 0.1410, 0.3593, 2.1796],
[-0.4336, -0.1106, 1.1228, -0.1804, 0.5361],
[-1.9375, 0.1241, -0.7275, 0.2676, 0.0118],
[-0.0511, -1.2384, -0.8405, 1.7962, -0.1198]],
[[ 0.0668, -2.1133, 1.1230, -0.1673, -0.3379],
[-2.5914, 1.0405, 1.4233, -1.0173, -0.7230],
[-0.6828, -0.9335, 0.5513, 0.1482, 0.4623],
[ 0.1665, -1.3033, 0.2815, 0.6613, 1.7401]],
[[-1.8565, 0.8329, 1.5913, 1.3783, 0.3283],
[ 0.3167, -1.4811, 1.4318, 1.7190, 0.9861],
[-0.5317, 1.2923, -1.2840, 0.2158, -0.0643],
[ 0.8721, 0.3452, -0.6808, -0.9248, -1.0642]]]),
tensor([0.0547]))

dataset.dataset[0][0]#第0个样本的特征张量

tensor([[[ 0.0806, 1.1339, 0.1410, 0.3593, 2.1796],
[-0.4336, -0.1106, 1.1228, -0.1804, 0.5361],
[-1.9375, 0.1241, -0.7275, 0.2676, 0.0118],
[-0.0511, -1.2384, -0.8405, 1.7962, -0.1198]],
[[ 0.0668, -2.1133, 1.1230, -0.1673, -0.3379],
[-2.5914, 1.0405, 1.4233, -1.0173, -0.7230],
[-0.6828, -0.9335, 0.5513, 0.1482, 0.4623],
[ 0.1665, -1.3033, 0.2815, 0.6613, 1.7401]],
[[-1.8565, 0.8329, 1.5913, 1.3783, 0.3283],
[ 0.3167, -1.4811, 1.4318, 1.7190, 0.9861],
[-0.5317, 1.2923, -1.2840, 0.2158, -0.0643],
[ 0.8721, 0.3452, -0.6808, -0.9248, -1.0642]]])

dataset.batch_size#如果忘记了设置的batch_size的大小，可以这样查看现有的batch_size

120

#如果从sklearn / pandas读取数据，应该如何操作？

from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from mpl_toolkits import mplot3d
import numpy as np
w1 = np.arange(-10,10,0.05)
w2 = np.arange(-10,10,0.05)
w1,w2 = np.meshgrid(w1,w2)
lossfn = (2 - w1 - w2)**2 + (4 - 3*w1 - w2)**2

#定义一个绘制三维图像的函数
#elev表示上下旋转的角度
#azim表示平行旋转的角度
def plot_3D(elev=45,azim=60,X=w1,y=w2):
    fig,ax = plt.subplots(1,1,constrained_layout=True,figsize=(8,8))
    ax = plt.subplot(projection="3d")
    ax.plot_surface(w1,w2,lossfn,cmap="rainbow",alpha=0.7)
    ax.view_init(elev=elev,azim=azim)
    ax.set_xlabel("w1",fontsize=20)
    ax.set_ylabel("w2",fontsize=20)
    ax.set_zlabel("lossfn",fontsize=20)
    plt.show()
    
from ipywidgets import interact,fixed
interact(plot_3D,elev=[0,15,30],azip=(-180,180),X=fixed(w1),y=fixed(w2))
plt.show()

interactive(children=(Dropdown(description=‘elev’, options=(0, 15, 30), value=0), IntSlider(value=60, descript…

3、2维函数优化实战

Himmelblau function: f(x,y) = (x² + y - 11)² + (x + y² - 7)²

import numpy as np
import matplotlib.pyplot as plt
def himmelblau(x):
    return(x[0] **2 +x[1]-11)**2 + (x[0]+x[1]**2 - 7)**2

x = np.arange(-6,6,0.1)
y = np.arange(-6,6,0.1)
print('x,y range:',x.shape,y.shape)
X,Y = np.meshgrid(x,y)
print('X,Y maps:',x.shape,y.shape)
Z = himmelblau([X,Y])

fig = plt.figure('himmelblau')
ax = fig.gca(projection = '3d')
ax.plot_surface(X,Y,Z)
ax.view_init(60,-30)
ax.set_xlabel('x')
ax.set_ylabel('y')
plt.show()

x,y range: (120,) (120,)
X,Y maps: (120,) (120,)

x = torch.tensor([0.,0.],requires_grad = True)  #初始化会影响最终找到的极小值和极大值。可以通过更改x的值观察运行结果
optimizer = torch.optim.Adam([x],lr = 1e-3)#目标是x.  x' =  x - 0.001▽x； y' = y-0.001▽y
for step in range(20000):
    pred = himmelblau(x)    #x送进来得到一个预测值
    optimizer.zero_grad()
    pred.backward()
    optimizer.step()       #把x,y更新为x',y'
    if step % 2000 == 0:
        print('step{}:x = {},f(x) = {}'
             .format(step,x.tolist(),pred.item()))

step0:x = [0.0009999999310821295, 0.0009999999310821295],f(x) = 170.0
step2000:x = [2.3331806659698486, 1.9540694952011108],f(x) = 13.730916023254395
step4000:x = [2.9820079803466797, 2.0270984172821045],f(x) = 0.014858869835734367
step6000:x = [2.999983549118042, 2.0000221729278564],f(x) = 1.1074007488787174e-08
step8000:x = [2.9999938011169434, 2.0000083446502686],f(x) = 1.5572823031106964e-09
step10000:x = [2.999997854232788, 2.000002861022949],f(x) = 1.8189894035458565e-10
step12000:x = [2.9999992847442627, 2.0000009536743164],f(x) = 1.6370904631912708e-11
step14000:x = [2.999999761581421, 2.000000238418579],f(x) = 1.8189894035458565e-12
step16000:x = [3.0, 2.0],f(x) = 0.0
step18000:x = [3.0, 2.0],f(x) = 0.0

loss != accuracy

logits = torch.rand(4,10)
F.softmax(logits,dim=1).argmax(dim=1)

tensor([1, 9, 5, 1])

logits.argmax(dim=1)  #上下两种写法等价

tensor([1, 9, 5, 1])

correct = torch.eq(logits.argmax(dim=1),torch.tensor([1,9,2,3]))
correct

tensor([ True, True, False, False])

correct.sum().float().item()/4 #准确率是50%

0.5

when to test?

test once per epoch
test once per several batch

visdom可视化

pip install visdom
pip uninstall visdom
python -m visdom.server #开启web服务器，开启visdon

·一条曲线
from visdom import Visdom
viz = Visdom()
viz.line([0.],[0.],win = 'train_loss',opts = dict(title='train loss'))#创建直线:给初始点,窗口，命名
viz.line([loss.item()],[global_step],win='train_loss',update='append')#(图像/numpy,x坐标,窗口,添加在当前的直线后面)

·多条曲线
from visdom import Visdom
viz = Visdom()
viz.line([[y1,y2]],[x],win='标识符',opts(标题，[y1_label,y2_label]))
viz.line([[0.0,0.0]],[0.],win='test',opts=dict(title='test loss&acc.',
                                          legend=['loss','acc.']))
viz.line([[test_loss,correct/len(test_loader.dataset)]],[global_step],win='test',update='append')

·visual x
from visdom import Visdom
viz = Visdom()
viz.images(data.view(-1,1,28,28),win='x')
viz.text(str(pred.detach().cpu().numpy()),win='pred',opts=dict(title='pred'))

过拟合与欠拟合