2021年MathorCup高校数学建模挑战赛B题三维团簇的能量预测解题全过程程序及论文
2021年MathorCup高校数学建模挑战赛B题 三维团簇的能量预测
想要解题全过程论文及程序的同学们,发车了。
原题再现
团簇,也称超细小簇,属纳米材料的尺度概念。团簇是由几个乃至上千个原子、分子或离子通过物理或化学结合力组成的相对稳定的微观或亚微观聚集体,其物理和化学性质随所含的原子数目而变化。
团簇是材料尺度纳米材料的一个概念。团簇的空间尺度是几埃至几百埃的范围,用无机分子来描述显得太小,用小块固体描述又显得太大,许多性质既不同于单个原子分子,又不同于固体和液体,也不能用两者性质的简单线性外延或内插得到。因此,人们把团簇看成是介于原子、分子与宏观固体物质之间的物质结构的新层次。团簇科学是凝聚态物理领域中非常重要的研究方向。
团簇可以分为金属团簇和非金属团簇,由于金属团簇具有良好的催化性能,因此备受关注。但由于团簇的势能面过于复杂,同时有时候还需要考虑相对论效应等,所以搜索团簇的全局最优结构(即能量最低)显得尤为困难。其中,传统的理论计算方法需要数值迭代求解薛定谔方程,并且随原子数增加,高精度的理论计算时间呈现指数增长,非常耗时。因此,目前需要对这种方法加以改进,例如:考虑全局优化算法,结合机器学习等方法,训练团簇结构和能量的关系,从而预测新型团簇的全局最优结构,有利于发现新型团簇材料的结构和性能。
请建立三维团簇能量预测的数学模型,并使用附件中的坐标和能量数据,解决下列问题。
备注:附件中数据集格式为 xyz,第一行是原子数,第二行是能量,后面是原子的三维坐标。可用文本阅读器打开,并用 VMD 等软件进行可视化。
VMD软件安装及
问题 1:针对金属团簇,附件给出了 1000 个金团簇 Au20的结构,请你们建立金团簇能量预测的数学模型,并预测金团簇 Au20 的全局最优结构,描述形状;
问题 2:在问题 1 的基础上,请你们设计算法,产生金团簇不同结构的异构体,自动搜索和预测金团簇 Au32的全局最优结构,并描述其几何形状,分析稳定性;
问题 3:针对非金属团簇,附件给出了 3751 个硼团簇 B45-的结构,请你们建立硼团簇能量预测的数学模型,并预测硼团簇 B45-的全局最优结构,描述形状;
问题 4:在问题 3 的基础上,请你们设计算法,产生硼团簇不同结构的异构体,自动搜索和预测硼团簇 B40-的全局最优结构,并描述其几何形状,分析稳定性。
我们首先数据处理,如果你会使用 VMD软件,那么就不需要数据处理转化为txt格式;但是你如果不会用就需要转化为txt格式文件再进行三维图像拟合。

我们这里不使用VMD绘图软件,采用数据处理后使用python绘制三维拟合模型图
程序代码
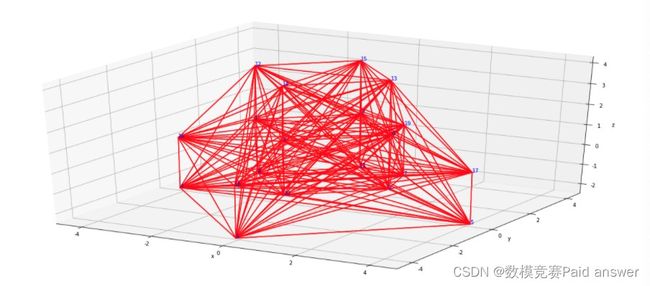
我们先随意拿一个题中所给数据作图:
import numpy as np
import mpl_toolkits.mplot3d
import matplotlib.pyplot as plt
import pandas as pd
plt.figure(figsize=(24, 10))
df = pd.read_excel("0.xlsx")
x=df['x']
y=df['y']
z=df['z']
ax=plt.subplot(111,projection='3d')
for i in range(len(x)):
for j in range(len(y)):
ax.plot((x[i],x[j]),(y[i],y[j]),(z[i],z[j]),color='pink')
for i in range(len(x)):
ax.text(x[i],y[i],z[i],i,color='blue')
ax.set_zlabel('z')
ax.set_ylabel('y')
ax.set_xlabel('x')
plt.show()
然后求一下三维位置信息及预测后的三维图像信息:
#ML method Au20
#present path file name
import os
import pandas as pd
import re
from sklearn.svm import SVC
from sklearn.model_selection import train_test_split
#find file name
file_name = os.listdir()
for f_name in file_name:
#judge file is not txt file
if f_name.endswith('.txt'):
# read data
with open(f_name,'r',encoding='utf-8') as f:
data = f.readlines()
# data slice get number type data
data = data[2:]
# get number use re to get
number_str_list = [re.findall(r"[- ]\d+\.?\d*",data[i].replace('\n','').strip(' ')) for i in range(20)]
#list store float data
number_float_list = []
#list store data label
number_target = []
# change str to float type
for item in number_str_list:
temp = []
count = 0
for n in item:
#change str data to float type
temp.append(float(n))
n = float(n)
#set data label
if n < 0:
count = count +1
#store data label
#number < 0 :number is 2 set label 0
if count > 1:
number_target.append(0)
#number < 0 :number is 1 set label 1
elif 0 < count < 2:
number_target.append(1)
##number < 0 :number is 0 set label 2
else:
number_target.append(2)
number_float_list.append(temp)
#split data
x_train,x_test, y_train, y_test =train_test_split(number_float_list,number_target,test_size=0.25, random_state=0)
#fit train data
svm = SVC().fit(x_train,y_train)
#use model to predict
predict = svm.predict(x_test)
#accuracy data set 1
acc = [1 for i in range(len(y_test)) if predict[i] == y_test[i]]
#cal accuracy
accuracy = len(acc) / len(y_test)
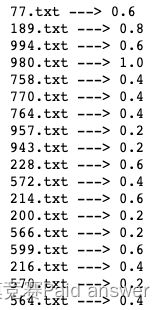
#output filename and accuracy
print(f_name,'--->',accuracy)
#Au20 ML
#import some tools
import os
import pandas as pd
import re
from sklearn.svm import SVC
from sklearn.model_selection import train_test_split
#model train and predict
def modelSvm(number_float_list,number_target):
#split data
x_train,x_test, y_train, y_test =train_test_split(number_float_list,number_target,test_size=0.25, random_state=0)
#fit train data
svm = SVC().fit(x_train,y_train)
#use model to predict
predict = svm.predict(x_test)
#return predict label
return predict,y_test
#find file name
file_name_list = os.listdir()
for fname in file_name_list:
#judge file is not txt file
if fname.endswith('.txt'):
# read data
with open(fname,'r',encoding='utf-8') as f:
data = f.readlines()
# data slice get number type data
data = data[2:]
# get number use re to get
number_str_list = [re.findall(r"[- ]\d+\.?\d*",data[i].replace('\n','').strip(' ')) for i in range(45)]
#list store float data
data_float_list = []
#list store data label
data_target = []
# change str to float type
for item in number_str_list:
temp = []
count = 0
for n in item:
#change str data to float type
temp.append(float(n))
n = float(n)
#set data label
if n < 0:
count = count +1
#store data label
#number < 0 :number is 2 set label 2
if count > 1:
data_target.append(2)
#number < 0 :number is 1 set label 1
elif 0 < count < 2:
data_target.append(1)
##number < 0 :number is 0 set label 0
else:
data_target.append(0)
data_float_list.append(temp)
#use model to predict
predict,y_test = modelSvm(data_float_list,data_target)
#accuracy data set 1
acc = [1 for i in range(len(y_test)) if predict[i] == y_test[i]]
#cal accuracy
accuracy = len(acc) / len(y_test)
#output filename and accuracy
print(fname,'--->',accuracy)

同分异构体与立体异构体
在有机化学中,将分子式相同、结构不同的化合物互称同分异构体,也称为结构异构体。立体异构体属于同分异构体的一种。分子中原子或原子团互相连接次序相同,但空间排列不同而引起的异构体称为立体异构体,有两类立体异构体。因键长、键角、分子内有双键、有环等原因引起的立体异构体称为构型异构体。一般来讲,构型异构体之间不能或很难互相转换。
空间两点距离计算原理为:

首先通过构建时间序列预测模型和 BP 神经网络预测模型,先后预测了金团簇Au20 和硼团簇 B45-的全局最优结构;然后基于蚁群算法和信息素更新机制改进的蚁群算法,先后预测了金团簇 Au32 和硼团簇 B40-的全局最优结构;最后我们将他们用 VMD 软件进行可视化并分析了其稳定性。
针对问题一,我们为了能够清晰的观察到金团簇 Au20的各种结构体之间的差异,我们选取部分数据进行可视化,并且对附件数据进行样本统计,发现缺失了名为 155.xyz的样本数据。本问我们选择构建基于时间序列的预测模型,该模型通过时间序列来反映三维坐标未来的变化情况,通过获取未来的三维坐标变化情况,代入三维坐标和能量之间的函数关系式当中,获取对应结构的能量值,通过循环上述操作,当金团簇 Au20的能量无法继续减小时,表明该值为金团簇 Au20的全局最优结构,我们得到该最优结构对应的能量为-1603.92,我们通过软件将其三维坐标可视化,描述了其形状。
针对问题二,我们需要设计一个优化算法,该算法能够求解金团簇 Au32的全局最优结构,因此我们团队选择设计蚁群算法。该算法的目标函数为求金团簇 Au32的能量最低,约束条件为金团簇 Au32的物理、化学特征以及原子数目。最后我们设置了算法的初始参数,通过编程求解得到其最优结构,能量为-2641.03,我们将其可视化描述形状,发现在中心轴的位置原子数量较多且排列整齐,其余原子则围绕中心原子转,因此该金团簇Au32的全局最优结构稳定性较好。
针对问题三,我们需要对非金属簇的硼团簇 B45-预测全局最优结构,区别于问题一的是,该问的元素所含的原子数较多,使用指数平滑时间序列预测模型的误差较大,因此本问我们选择构建 BP 神经网络预测模型。我们将三维坐标数据作为输入节点数据,能量数据作为输出节点数据,构建神经网络,将硼团簇 B45-的附件数据代入神经网络中进行训练,得到训练误差为 0.01,训练的拟合优度达到 0.9,因此网络可靠。我们预测得到硼团簇 B45-的全局最优结构的能量为-118377.23,并可视化该结构描述其形状
针对问题四,由于硼团簇 B40-原子数量较多,普通的蚁群算法对本问求全局最优解较为困难,且效率较低,因此我们本问需要针对问题二所设计的蚁群算法进行改进,我们基于信息素更新机制改进蚁群算法,提出一种局部更新和全局动态更新相结合的信息素动态区块更新方式。最终实现预测硼团簇 B40-的全局最优结构为-117600.98,将其结构进行可视化,发现该结构为环形结构,且能量值低,因此有良好的稳定性。