机器学习之原型聚类算法（K均值和高斯混合）

“原型"是指样本空间中具有代表性的点。
原型聚类算法是假设聚类结构能通过一组原型进行刻画，在现实聚类任务中极为常用。
通常情形下，算法先对原型进行初始化，然后对原型进行迭代更新求解。采用不同的原型表示、不同的求解方式，将产生不同的算法。

1、原型聚类算法介绍

1.1、k均值(k-means )

给定样本集$D=\left\{x_1,x_2,\cdots ,x_m\right\}$, "k均值"算法针对聚类所得簇划分$C=\left\{C_1,C_2,\cdots ,C_k\right\}$ 最小化平方误差$$E=\sum _{i=1}^k\sum _{x\in C_i}{\Vert x-{\mu }_i\Vert }_2^2$$
其中${\mu }_i$是簇$C_i$的均值向量。在一定程度上刻画了簇内样本围绕簇均值向量的紧密程度， E值越小则簇内样本相似度越高。k均值算法通过迭代优化来近似求解式最小化平方误差。

1.2、学习向量量化(LVQ)

“学习向量量化” (Learning Vector Quantization，简称LVQ)是试图找到一组原型向量来刻画聚类结构，但与一般聚类算法不同的是， LVQ假设数据样本带有类别标记，学习过程利用样本的监督信息来辅助聚类。
在每一轮选代时，算法随机选取一个有标记训练样本，找出与其距离最近的原型向量，并根据两者的类别标记是否一致来对原型向量进行相应的更新。$p^{\prime }=p_{i\ast }\pm \eta \cdot (x_j-p_{i\ast })$，$\eta$是学习率。若算法的停止条件已满足(例如己达到最大迭代轮数，或原型向量更新很小甚至不再更新)，则将当前原型向量作为最终结果返回。
比较K均值与LVQ算法差异
两种算法的主要差异是更新原型向量的方法，K均值是根据分配到簇内的所有样本计算新的均值向量；LVQ是随机抽取一个样本，找到与其最近的原型向量，如果标记相同，则计算出更靠近随机样本的新原型向量，否则相反计算出更远的新原型向量。

1.3、高斯混合聚类(Mixture-of-Gaussian)

与k 均值、LVQ 用原型向量来刻画聚类结构不同，高斯混合聚类采用概率模型来表达聚类原型。
高斯分布由均值向量$\mu$和协方差矩阵$\sum$两个参数确定。高斯混合分布定义：
$$pm(x)=\sum _{i=1}^k{\alpha }_i\cdot p(x|{\mu }_i,{\Sigma }_i)$$
该分布共由k 个混合成分组成，每个混合成分对应一个高斯分布。其中${\mu }_i$与${\Sigma }_i$是第i个高斯混合成分的参数，而${\alpha }_i$> 0 为相应的"混合系数"(mixture coefficient)，${\sum }_{i=1}^k{\alpha }_i=1$
求解：给定样本集D，可采用极大似然估计，即最大化(对数)似然。
EM算法(期望最大化，Expectation-Maximum)
常采用EM算法进行迭代优化求解，如下：
在每步迭代中，先根据当前参数来计算每个样本属于每个高斯成分的后验概率 (E步)，再根据公式更新模型参数(M步)。
从原型聚类的角度来看，高斯混合聚类是采用概率模型(高斯分布)对原型进行刻画，簇划分则由原型对应后验概率确定。
先知道结果，然后由结果估计（推算）原因的概率分布，就是后验概率；先于结果，确定原因的概率分布，就是先验概率。

2、Sklearn代码实现

import matplotlib.pyplot as plt
import pandas as pd
from sklearn.cluster import KMeans
from sklearn import datasets, metrics
from sklearn.mixture import GaussianMixture


def test_kmeans():
    # 加载样本数据
    sample = load_data()
    data = sample.data
    # 创建模型
    n_clusters = 3
    model = KMeans(n_clusters=n_clusters, random_state=7)
    # 模型训练
    model.fit(data)
    # 聚类结果
    centers = model.cluster_centers_
    print('聚类中心', centers)
    # 聚类生成的标签值
    labels = model.labels_
    print("各簇的样本数目：", pd.Series(labels).value_counts())
    # 获取迭代次数
    print("迭代次数", model.n_iter_)
    # 聚类的分值，分值越大，效果越好
    print("分值", model.score(data))
    # 模型评估 - 轮廓系数，该值处于-1~1之间，值越大，表示聚类效果越好
    silhouette = metrics.silhouette_score(data, labels, metric='euclidean')
    print('轮廓系数silhouette', silhouette)
    # 模型评估 - CH指标，分数越高越好
    ch = metrics.calinski_harabasz_score(data, labels)
    print('Calinski Harabasz', ch)

    # 散点颜色
    colors = ['r', 'b', 'g', 'c', 'm']
    # 散点形状
    markers = ['o', 's', '^', 'x']
    # 绘制簇散点图
    plt.figure('kmeans')
    for i in range(n_clusters):
        # 按簇循环绘制
        x = data[labels == i]
        # 样本的前两个特征值
        plt.scatter(x=x[:, 0], y=x[:, 1], marker=markers[i % 4], color=colors[i % 5], alpha=0.5)
    # 绘制聚类中心点，S是大小，默认为50
    plt.scatter(x=centers[:, 0], y=centers[:, 1], marker='*', s=80, color='k')
    # 坐标轴，获取样本特征名称
    plt.xlabel("{}".format(sample.feature_names[0]))
    plt.ylabel("{}".format(sample.feature_names[1]))
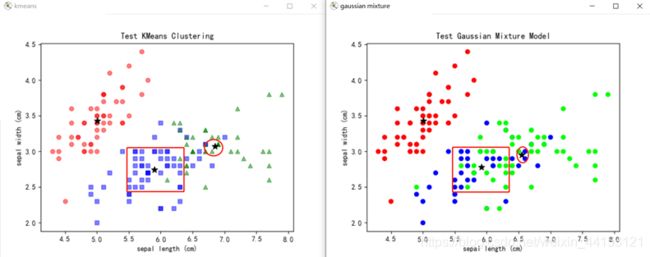
    plt.title("Test KMeans Clustering")
    # plt.show()


def test_gmm():
    # 加载样本数据
    sample = load_data()
    data = sample.data
    # 创建模型
    n_clusters = 3
    # 设置gmm函数
    model = GaussianMixture(n_components=n_clusters)
    # 模型训练
    model.fit(data)
    # 聚类结果
    centers = model.means_
    print('聚类中心', centers)

    # 绘制预测值散点图
    plt.figure('gaussian mixture')
    pred_y = model.predict(data)
    plt.scatter(data[:, 0], data[:, 1], c=pred_y, cmap='brg')
    # 绘制聚类中心点，S是大小，默认为50
    plt.scatter(x=centers[:, 0], y=centers[:, 1], marker='*', s=80, color='k')
    # 坐标轴，获取样本特征名称
    plt.xlabel("{}".format(sample.feature_names[0]))
    plt.ylabel("{}".format(sample.feature_names[1]))
    plt.title("Test Gaussian Mixture Model")
    plt.show()


def load_data():
    """
    加载鸢尾花数据集
    """
    return datasets.load_iris()


if __name__ == '__main__':
    import matplotlib as mpl

    # 汉字字体,优先使用楷体，如果找不到楷体，则使用黑体
    mpl.rcParams['font.sans-serif'] = ['KaiTi', 'SimHei', 'FangSong']

    # KMeans算法
    test_kmeans()
    # 高斯混合模型
    test_gmm()

运行结果，两种算法生成的簇中心和样本标记有差异，尤其是下图红框圈定部分，如下：