【机器学习】聚类【Ⅱ】原型聚类经典算法

主要来自周志华《机器学习》一书，数学推导主要来自简书博主“形式运算”的原创博客，包含自己的理解。
有任何的书写错误、排版错误、概念错误等，希望大家包含指正。

由于字数限制，分成五篇博客。
【机器学习】聚类【Ⅰ】基础知识与距离度量
【机器学习】聚类【Ⅱ】原型聚类经典算法
【机器学习】聚类【Ⅲ】高斯混合模型讲解
【机器学习】聚类【Ⅳ】高斯混合模型数学推导
【机器学习】聚类【Ⅴ】密度聚类与层次聚类

4 原型聚类

原型聚类亦称“基于原型的聚类”（prototype-based clustering），“原型”是指样本空间中具有代表性的点，此类算法假设聚类结构能通过一组原型刻画，在现实聚类任务中极为常用。通常情形下，算法先对原型进行初始化，然后对原型进行迭代更新求解。采用不同的原型表示、不同的求解方式，将产生不同的算法。

原型聚类强调两点，“原型”和“迭代”。“原型”思想是指用具有代表性的点表示簇，“迭代”思想是指在原型聚类中往往很难找到最优解，所以会通过迭代的方式找到最佳近似解。

4.1 $k$ 均值算法

给定样本集 $D=\{{xx}_1,{xx}_2,\cdot \cdot \cdot ,{xx}_m\}$，“$k$ 均值”（k-means）算法针对聚类所得簇划分 $\mathcal{C}=\{C_1,C_2,\cdot \cdot \cdot ,C_k\}$ 最小化平方误差
$$E=\sum _{i=1}^k\sum _{xx\in C_i}\Vert xx-{\mu \mu }_i{\Vert }_2^2\text{\hspace{1em}(27)}$$
其中 ${\mu \mu }_i=\frac{1}{|C_i|}{\sum }_{\in \in C_i}$ 是簇 $C_i$ 的均值向量。直观来看，式 $(27)$ 在一定程度上刻画了簇内样本围绕簇均值向量的紧密程度，$E$ 值越小则簇内样本相似度越高。

最小化式 $(27)$ 并不容易，找到它的最优解需考察样本集 $D$ 所有可能的簇划分，这是一个 NP 难问题，也就是说最小化式 $(27)$ 只是无法达成的理想目标。因此，$k$ 均值算法采用了贪心策略，通过迭代优化来近似求解式 $(27)$ 。算法流程如算法 $1$ 所示，其中第 $1$ 行对均值向量进行初始化，在第 $4$ - $8$ 行与第 $9$ - $16$ 行依次对当前簇划分及均值向量迭代更新，若迭代更新后聚类结果保持不变，则在第 $18$ 行将当前簇划分结果返回。

$$\begin{array}{llcccccccccccccccccc}\text{输入:}& 样本集D=\{{xx}_1,{xx}_2,\cdot \cdot \cdot ,{xx}_m\};& & & & & & & & & & & & & & & & & & \\ & 聚类簇数k.& & & & & & & & & & & & & & & & & & \\ \text{过程:}& & & & & & & & & & & & & & & & & & & \end{array}$$

$$\begin{array}{rl}1:& 从D中随机选择k个样本作为初始均值向量\{{\mu \mu }_1,{\mu \mu }_2,\cdot \cdot \cdot ,{\mu \mu }_k\}\\ 2:& \text{repeat}\\ 3:& 令C_i=\varnothing (1\le i\le k)\\ 4:& \text{for}j=1,2,\cdot \cdot \cdot ,m\text{do}\\ 5:& 计算样本{xx}_j与各均值向量{\mu \mu }_i(1\le i\le k)的距离:d_{ji}=\Vert {xx}_j-{\mu \mu }_i{\Vert }_2;\\ 6:& 根据距离最近的均值向量确定{xx}_j的簇标记:{\lambda }_j=\arg {\max }_{i\in \{1,2,\cdot \cdot \cdot ,k\}}{d}_{ji};\\ 7:& 将样本{xx}_j划入相应的簇:C_{{\lambda }_j}=C_{{\lambda }_j}\bigcup \{{xx}_j\};\\ 8:& \text{end}\text{for}\\ 9:& \text{for}i=1,2,\cdot \cdot \cdot ,k\text{do}\\ 10:& 计算新均值向量:{\mu \mu }_i^{\prime }=\frac{1}{|C_i|}{\sum }_{xx\in C_i}xx;\\ 11:& \text{if}{\mu \mu }_i^{\prime }\ne {\mu \mu }_i\text{then}\\ 12:& 将当前均值向量{\mu \mu }_i更新为{\mu \mu }_i^{\prime }\\ 13:& \text{else}\\ 14:& 保持当前均值向量不变\\ 15:& \text{end}\text{if}\\ 16:& \text{end}\text{for}\\ 17:& \text{until}当前均值向量均未更新\end{array}$$

$$\begin{array}{lcccccccccccccccccccc}\text{输出:}簇划分\mathcal{C}=\{C_1,C_2,\cdot \cdot \cdot ,C_k\}& & & & & & & & & & & & & & & & & & & & \end{array}$$

算法 1    k 均值算法

为避免运行时间过长，通常设置一个最大运行轮数或最小调整幅度阈值，若达到最大轮数或调整幅度小于阈值，则停止运行。

算法基本思路为，将每个样本分到距离最近的均值向量所代表的簇中，用簇内全部样本的均值作为新的均值向量不断迭代，直到向量均值不再改变或满足算法停止的其他条件。

注意：原型并不一定是均值向量，均值向量只是原型的一种表示方式，也就是说，我们可以选择用均值向量作为簇的原型，也可以选择其他方式。

下面以表 $1$ 的西瓜数据集为例来演示 $k$ 均值算法的学习过程。为方便叙述，我们将编号为 $i$ 的样本称为 ${xx}_i$，这是一个包含“密度”与“含糖率”两个属性值的二维向量。

编号	密度	含糖率	编号	密度	含糖率	编号	密度	含糖率
1	0.697	0.460	11	0.245	0.057	21	0.748	0.232
2	0.774	0.376	12	0.343	0.099	22	0.714	0.346
3	0.634	0.264	13	0.639	0.161	23	0.483	0.312
4	0.608	0.318	14	0.657	0.198	24	0.478	0.437
5	0.556	0.215	15	0.360	0.370	25	0.525	0.369
6	0.403	0.237	16	0.593	0.042	26	0.751	0.489
7	0.481	0.149	17	0.719	0.103	27	0.532	0.472
8	0.437	0.211	18	0.359	0.188	28	0.473	0.376
9	0.666	0.091	19	0.339	0.241	29	0.725	0.445
10	0.243	0.267	20	0.282	0.257	30	0.446	0.459

表 1    西瓜数据集

假定聚类簇数 $k=3$，算法开始时随机选取三个样本 ${xx}_6,{xx}_{12},{xx}_{27}$ 作为初始均值向量，即
$${\mu \mu }_1=(0.403;0.237),{\mu \mu }_2=(0.343;0.099),{\mu \mu }_3=(0.532;0.472)$$
考察样本 ${xx}_1=(0.697;0.460)$，它与当前均值向量 ${\mu \mu }_1,{\mu \mu }_2,{\mu \mu }_3$ 的距离分别为 $0.369,0.506,0.166$，因此 $x_1$ 将被划入簇 $C_3$ 中。类似的，对数据集中的所有样本考察一遍后，可得当前簇划分为
$$\begin{array}{rl}{C}_1& =\{x_5,x_6,x_7,x_8,x_9,x_{10},x_{13},x_{14},x_{15},x_{17},x_{18},x_{19},x_{20},x_{23}\}\\ C_2& =\{x_{11},x_{12},x_{16}\}\\ C_3& =\{x_1,x_2,x_3,x_4,x_{21},x_{22},x_{24},x_{25},x_{26},x_{27},x_{28},x_{29},x_{30}\}\end{array}$$
于是，可从 $C_1$、$C_2$、$C_3$ 分别求出新的均值向量
$${\mu \mu }_1^{\prime }=(0.473;0.214),{\mu \mu }_2^{\prime }(0.394;0.066),{\mu \mu }_3^{\prime }=(0.623;0.388)$$
更新当前均值向量后，不断重复上述过程，如图 $2$ 所示，第五轮迭代产生的结果与第四轮迭代相同，于是算法停止，得到最终的簇划分。

图 2    西瓜数据集上 k 均值算法(k=3)在各轮迭代后的结果。样本点与均值向量分别用“●”与“+”表示，红色虚线显示出簇划分。

优点：

• 解决聚类问题的一种经典算法，简单、快速；
• 对处理大数据集，该算法是相对可伸缩和高效率的；
• 当结果簇密集时效果较好。

缺点：

• 必须事先给出 $k$（要生成的簇数），而且对初值敏感，对于不同的初始值，可能会导致不同结果；
• 不适合于发现非凸面形状的簇或者大小差别很大的簇。而且，它对于“噪声”和孤立点数据是敏感的。

4.2 $k$-modes 算法

$k$-means 算法是一种简单且实用的聚类算法，但是传统的 $k$-means 算法只适用于数值型属性的数据集，而对于类别型属性的数据集，计算簇的均值以及点之间的欧式距离就变得不合适了。$k$-modes 作为 $k$-means 的一种扩展，适用于类别型属性的数据集。

数值型属性和类别型属性分别是前面提到的有序属性和无序属性。

由于 $k$-modes 算法与 $k$-means 算法流程一致，唯一的不同在于 $k$-modes 算法使用类别型样本距离的度量方法和更新原型的方法。算法采用”汉明距离“（hamming distance）度量样本距离，汉明距离常用于数据传输差错控制编码中，这里拓展其概念和用途。类别型样本间的汉明距离定义为
$$\mathrm{dis}{\mathrm{t}}_{\mathrm{hm}}({xx}_i,{xx}_j)=\sum _{u=1}^n\delta (x_{iu},x_{ju})\text{\hspace{1em}(28)}$$
其中，$\delta (a,b)$ 定义为
$$\delta (a,b)=\{\begin{array}{ll}1,& a=b\\ 0,& a\ne b\end{array}\text{\hspace{1em}(29)}$$
观察上式可知，两个样本的汉明距离可以理解为，对应属性不同取值的个数和。

在更新原型时，选择每个族中每个属性出现频率最大的属性作为簇的代表属性。

4.3 $k$-prototype 算法

$k$-prototype 算法是处理混合属性聚类的典型算法。继承 $k$-means 算法和 $k$-modes 算法的思想，并且加入了描述数据簇的原型和混合属性数据之间的相异度计算公式。混合属性是指既包括数值型属性又包括类别型属性。

给定样本集 $D=\{{xx}_1,{xx}_2,\cdot \cdot \cdot ,{xx}_m\}$，样本 ${xx}_i=\{x_{i1},\cdot \cdot \cdot ,x_{in}\}$，第 $i$ 个簇 $C_i$ 的原型 ${pp}_i=\{p_{i1},\cdot \cdot \cdot ,p_{im}\}$，$k$-prototype的理想优化目标是最小化误差，误差度量也即损失函数为
$$E=\sum _{l=1}^k\sum _{i=1}^m{y}_{il}d({xx}_i,{pp}_l)\text{\hspace{1em}(30)}$$
其中，$y_{il}$ 表示样本 ${xx}_i$ 是否在簇 $C_l$ 中，如果在簇中，则 $y_{il}=1$ 否则 $y_{il}=0$ 。$d({xx}_i,{pp}_l)$ 度量样本 ${xx}_i$ 与簇 $C_l$ 的原型 ${pp}_l$ 的距离，$k$-prototype 算法考虑到一个样本具有数值型和类别型两类属性，因此对于数值型属性的距离采用欧拉距离的平方进行度量，对于类别型属性的距离采用汉明距离与某个系数的乘积进行度量。假定有 $n_c$ 个数值型属性、$n-n_c$ 个类别型属性，不失一般性，令数值型属性排列在类别型属性之前，则
$$d({xx}_i,{pp}_l)=\sum _{u=1}^{n_c}(x_{iu}-p_{lu}{)}^2+{\gamma }_l\sum _{u=n_c+1}^n\delta (x_{iu},p_{lu})\text{\hspace{1em}(30)}$$
其中，${\gamma }_l$ 为度量簇 $C_l$ 中样本与原型的类别型属性距离时的权重，即上文中提到的”系数“。

在更新原型的方式上，对于数值型属性计算均值，对于类别型属性以频率最大的属性作为代表，相当于融合了 $k$-means 算法和 $k$-modes 算法，其算法流程依然与 $k$-means 一致。

为了与前文的符号统一，这里定义的符号与参考论文有些不同。这部分仅挑选了论文中有关思想及算法的部分进行了讲解。

4.4 $k$-medoids 算法

不去详细区分”mediods“和”medoids“，网上对于两个单词的用法区分度不高。

$k$-means 算法对离群点敏感，当离群点分配到一个簇时，它们可能严重地扭曲簇的均值，这不经意间影响了其他样本的分配。$k$-medoids 算法应运而生，围绕中心点划分（Partitioning Around Medoids，简称 PAM）算法是 $k$-medoids 聚类的一种实现方式。

$k$-medoids 算法流程相较于 $k$-means 算法有一些区别。首先需要明确，在 $k$-medoids 算法中，簇的原型一定是样本，这与前面讲到的聚类算法不同。

算法流程大致描述如下：

• 随机选取 $k$ 个样本作为原型
• 计算每个非原型样本到原型样本的距离，把每个非原型样本分配到距离它最近的原型所代表的簇中
• 尝试用全部非原型样本去替换每个原型样本作为新的原型，对于全部替换方式，计算替换前后的目标函数值变化量（后减前）
• 如果存在变化量小于零的替换方式，则选择变化量最小的对应的替换方式，用新样本替换原型样本作为新原型，迭代第二步到第四步；反之，如果不存在则不替换，算法结束

给定样本集 $D=\{{xx}_1,{xx}_2,\cdot \cdot \cdot ,{xx}_m\}$，$k$ 个簇的原型样本为 $pp=\{{pp}_1,\cdot \cdot \cdot ,{pp}_k\}$ 且 ${pp}_i\in D$，$k$-medoids 算法的目标函数
$$E=\sum _{i=1}^k\sum _{xx\in C_i}\mathrm{dist}(xx,{pp}_i)$$
我们认为样本自己间的距离为 $0$，所以上式不再特意区分簇中的样本是原型还是非原型。可以根据需要选择不同的距离度量方式。

举个简单的例子，假定忽略距离度量方法，表 $2$ 直接以邻接矩阵的形式给出 $5$ 个样本两两之间的距离。

样本点	A	B	C	D	E
A	0	1	2	2	3
B	1	0	2	4	3
C	2	2	0	1	5
D	2	4	1	0	3
E	3	3	5	3	0

表 2    距离邻接矩阵

假定从 $5$ 个样本中随机抽取的 $2$ 个原型为 $\{A,B\}$，则样本被划分为 $\{A,C,D\}$ 和 $\{B,E\}$ ，如图 $3$ 所示。此时的目标函数值为 $2+2+3=7$。

图 3    初始划分

尝试用每个非原型样本替换原型样本作为簇的原型，对于这个示例而言，总共有 $3\times 2=6$ 种替换方式，如图 $4$ 所示。分别计算出六种替换方式的目标函数值变化量：用样本 $C$ 替换原型样本 $A$ 得到变化量为 ${\Delta }_{AC}=(1+1+3)-7=-2$，其他五个类似，${\Delta }_{AD}=-2$，${\Delta }_{AE}=-1$，${\Delta }_{BC}=-2$，${\Delta }_{BD}=-2$，${\Delta }_{BE}=-2$。计算完毕后，要选取一个最小的代价，显然有多种替换可以选择，选择 $C$ 替换 $A$，根据图 $4$ 左上角子图所示，样本被划分为 $\{B,A,E\}$ 和 $\{C,D\}$ 两个簇。

图 4    六种替换方式

通过上述计算，已经完成了 PAM 算法的第一次迭代。在下一迭代中，将用其他的非原型样本 $\{A,D,E\}$ 替换原型 $\{B,C\}$，找出具有最小变化量的替换。一直重复上述过程，直到目标函数不再减小为止。

4.5 学习向量量化

”学习向量量化“属于监督学习的算法，也就是说存在训练与预测两部分，而无监督学习没有训练与预测之说，可以直接进行分类。但是无监督也可能存在参数要学习，比如上面的 $k$-means 算法等都是采用 EM 算法进行参数学习，上述聚类算法中的参数为簇原型。

之所以将这部分放在”聚类“部分讲解，是因为其训练算法与 $k$-means 算法流程基本一致。

与k均值算法类似，“学习向量量化”（Learning Vector Quantization，简称 LVQ）也是试图找到一组原型向量来刻画聚类结构，但与一般聚类算法不同的是，LVQ 假设数据样本带有类别标记，学习过程利用样本的这些监督信息来辅助聚类。

给定样本集 $D=\{({xx}_1,y_1),({xx}_2,y_2),\cdot \cdot \cdot ,({xx}_m,y_m)\}$，每个样本 ${xx}_j$ 是由 $n$ 个属性描述的特征向量 $(x_{j1};x_{j2};\cdot \cdot \cdot ;x_{jn})$，$y_j\in \mathcal{Y}$ 是样本 ${xx}_j$ 的类别标记。LVQ 的目标是学得一组 $n$ 维原型向量 $\{{pp}_1,{pp}_2,\cdot \cdot \cdot ,{pp}_q\}$，每个原型向量代表一个聚类簇，簇标记 $t_i\in \mathcal{Y}$ 。

允许 $t_i=t_j(i\ne j)$ ，这是因为 LVQ 是监督学习。

LVQ 算法描述如算法 $2$ 所示。算法第 $1$ 行先对原型向量进行初始化，例如对第 $q$ 个簇可从类别标记为 $t_q$ 的样本中随机选取一个作为原型向量。算法第$2\sim 12$ 行对原型向量进行迭代优化。在每一轮迭代中，算法随机选取一个有标记训练样本，找出与其距离最近的原型向量，并根据两者的类别标记是否一致来对原型向量进行相应的更新。在第 $12$ 行中，若算法的停止条件已满足（例如已达到最大迭代轮数，或原型向量更新很小甚至不再更新），则将当前原型向量作为最终结果返回。

$$\begin{array}{llc}\text{输入:}& 样本集D=\{({xx}_1,y_1),({xx}_2,y_2),\cdot \cdot \cdot ,({xx}_m,y_m)\};& \\ & 原型向量个数q，各原型向量预设的类别标记\{t_1,t_2,\cdot \cdot \cdot ,t_q\};& \\ & 学习率\eta \in (0,1).& \\ \text{过程:}& & \end{array}$$

$$\begin{array}{rl}1:& 初始化一组原型向量\{{pp}_1,{pp}_2,\cdot \cdot \cdot ,{pp}_k\}\\ 2:& \text{repeat}\\ 3:& 从样本集D随机选取样本({xx}_j,y_j);\\ 4:& 计算样本{xx}_j与{pp}_i(1\le i\le q)的距离:d_{ji}=\Vert {xx}_j-{pp}_i{\Vert }_2;\\ 5:& 找出与{xx}_j距离最近的原型向量{pp}_{i^{\ast }}，i^{\ast }=\arg {\min }_{i\in \{1,2,\cdot \cdot \cdot ,q\}}{d}_{ji};\\ 6:& \text{if}{y}_j=t_{i^{\ast }}\text{then}\\ 7:& {pp}^{\prime }={pp}_{i^{\ast }}+\eta \cdot ({xx}_j-{pp}_{i^{\ast }})\\ 8:& \text{else}\\ 9:& {pp}^{\prime }={pp}_{i^{\ast }}-\eta \cdot ({xx}_j-{pp}_{i^{\ast }})\\ 10:& \text{end}\text{if}\\ 11:& 将原型向量{pp}_{i^{\ast }}更新为{pp}^{\prime }\\ 12:& \text{until}满足停止条件\end{array}$$

$$\begin{array}{lccccccccccccccccc}\text{输出:}原型向量\{{pp}_1,{pp}_2,\cdot \cdot \cdot ,{pp}_q\}& & & & & & & & & & & & & & & & & \end{array}$$

算法 2    学习向量量化算法

显然，LVQ 的关键是第 $6\sim 10$ 行，即如何更新原型向量。直观上看，对样本 ${xx}_j$，若最近的原型向量 ${pp}_{i^{\ast }}$ 与 ${xx}_j$ 的类别标记相同，则令 ${pp}_{i^{\ast }}$ 向 ${xx}_j$ 的方向靠拢，如第 $7$ 行所示，此时新原型向量为
$${pp}^{\prime }={pp}_{i^{\ast }}+\eta \cdot ({xx}_j-{pp}_{i^{\ast }})\text{\hspace{1em}(31)}$$
${pp}^{\prime }$ 与 ${xx}_j$ 之间的距离为
$$\begin{array}{rl}\Vert {pp}^{\prime }-{xx}_j{\Vert }_2& =\Vert {pp}_{i^{\ast }}+\eta \cdot ({xx}_j-{pp}_{i^{\ast }})-{xx}_j{\Vert }_2\\ & =(1-\eta )\cdot \Vert {pp}_{i^{\ast }}-{xx}_j{\Vert }_2\end{array}\text{\hspace{1em}(32)}$$
令学习率 $\eta \in (0,1)$，则原型向量 ${pp}_{i^{\ast }}$ 在更新为 ${pp}^{\prime }$ 之后将更接近 ${xx}_j$ 。

类似的，若 ${pp}_{i^{\ast }}$ 与 ${xx}_j$ 的类别标记不同，则更新后的原型向量与 ${xx}_j$ 之间的距离将增大为 $(1+\eta )\cdot \Vert {pp}_{i^{\ast }}-{xx}_j{\Vert }_2$，从而更远离 ${xx}_j$ 。

之所以式 $(31)$ 不直接使用 $\pm \eta \cdot {xx}_j$ ，而使用 $\pm \eta \cdot ({xx}_j-{pp}_{i^{\ast }})$，正是因为要保证计算 ${pp}^{\prime }$ 与 ${xx}_j$ 之间距离时能方便比较变化前后的距离大小，即得到式 $(32)$。总而言之，就是为了更好的解释性。

在学得一组原型向量 $\{{pp}_1,{pp}_2,\cdot \cdot \cdot ,{pp}_q\}$ 后，即可实现对样本空间 $\mathcal{X}$ 的簇划分。对任意样本 $xx$，它将被划入与其距离最近的原型向量所代表的簇中；换言之，每个原型向量 ${pp}_i$ 定义了与之相关的一个区域 $R_i$，该区域中每个样本与 ${pp}_i$ 的距离不大于它与其他原型向量 ${pp}_{i^{\prime }}(i^{\prime }\ne i)$ 的距离，即
$$R_i=\{xx\in \mathcal{X}\mid \Vert xx-{pp}_i{\Vert }_2\le \Vert xx-{pp}_{i^{\prime }}{\Vert }_2,i^{\prime }\ne i\}\text{\hspace{1em}(33)}$$
由此形成了对样本空间 $\mathcal{X}$ 的簇划分 $\{R_1,R_2,\cdot \cdot \cdot ,R_q\}$，该划分通常称为“Voronoi 剖分”（Voronoi tessellation）。

若将 $R_i$ 中样本全用原型向量 ${pp}_i$ 表示，则可实现数据的“有损压缩”（lossy compression），这称为“向量量化”（vector quantization）；LVQ 由此而得名。

下面我们以表 $1$ 的西瓜数据集为例来演示 LVQ 的学习（训练）过程。令 $9\sim 21$ 号样本的类别是“好瓜=否”标记为 $C_2$，其他样本的类别是“好瓜=是”标记为 $C_1$ 。假定 $q=5$，即学习目标是找到 $5$ 个原型向量 ${pp}_1,{pp}_2,{pp}_3,{pp}_4,{pp}_5$，并假定其对应的类别标记分别为 $C_1,C_2,C_2,C_1,C_1$，即希望为“好瓜=是”找到 $3$ 个簇，“好瓜=否”找到 $2$ 个簇。

算法开始时，根据样本的类别标记和簇的预设类别标记对原型向量进行随机初始化，假定初始化为样本 ${xx}_5,{xx}_{12},{xx}_{18},{xx}_{23},{xx}_{29}$ 。在第一轮迭代中，假定随机选取的样本为 ${xx}_1$，该样本与当前原型向量 ${pp}_1,{pp}_2,{pp}_3,{pp}_4,{pp}_5$ 的距离分别为 $0.283,0.506,0.434,0.260,0.032$ 。由于 ${pp}_5$ 与 ${xx}_1$ 距离最近且两者具有相同的类别标记 $C_2$，假定学习率 $\eta =0.1$，则 LVQ 更新 ${pp}_5$ 得到新原型向量
$$\begin{array}{rl}{pp}^{\prime }& ={pp}_5+\eta \cdot ({xx}_1-{pp}_5)\\ & =(0.725;0.445)+0.1\cdot \left((0.697;0.460)-(0.725;0.445)\right)\\ & =(0.722;0.442)\end{array}$$
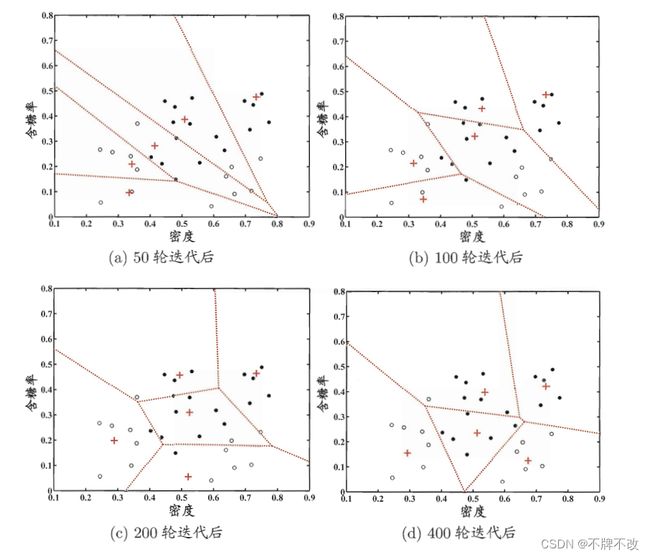
将 ${pp}_5$ 更新为 ${pp}^{\prime }$ 后，不断重复上述过程，不同轮数之后的聚类结果如图 $5$ 所示。

图 5    西瓜数据集上 LVQ 算法(q=5)在不同轮数迭代后的聚类结果。C₁, C₂类样本点与原型向量分别用“●”，“○”与“+”表示，红色虚线显示出聚类形成的 Voronoi 剖分。

注意，算法 $2$ 描述过程为模型训练的过程，该算法输出一组原型向量。使用模型进行预测时，我们计算待预测样本与每个簇的原型向量之间的距离，将样本分配到距离最近的簇中，簇的标签即为该样本的预测标签。