哈希表知识与相关题目（Python）

1. 哈希表知识

1.1 哈希表简介

哈希表（Hash Table）：也叫做散列表。是根据键（key）、值（value）直接进行访问的数据结构。也就是说，它通过键key和一个映射函数Hash(key)计算出对应的值value，把key和value映射到表中一个位置来访问记录，以加快查找的速度。这个映射函数叫做哈希函数，存放记录的数组叫做哈希表。

哈希表的关键思想是使用哈希函数，将键 key 映射到对应表的某个区块中。

哈希表的原理实例如下图所示：

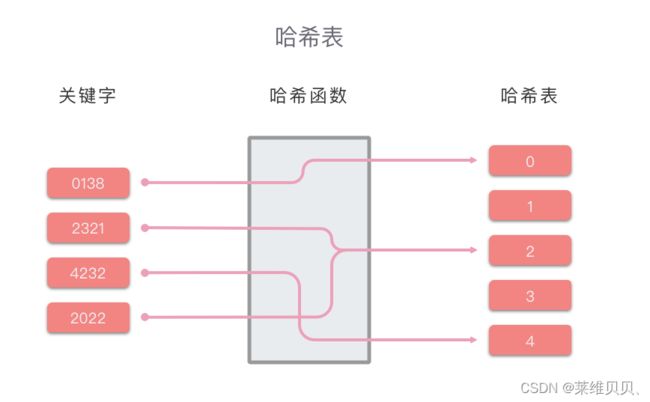
上图例子的解释：value = Hash(key) = key // 1000 作为哈希函数。// 符号代表整除。

• 插入：通过哈希函数解析关键字，并将对应值存放到该区块中
  比如：value = Hash(key) = 0138 // 100 = 0，得出应将0138分配到0所在的区块中。
• 查找：通过哈希函数解析关键字，并在特点的区块搜索关键字对应的值。
  比如： 查找4232，通过哈希函数，得出2022应该在4所对应的区块中。然后为满从4对应的区块中继续搜索，并在2对应的区块中成功找到。
  比如：查找 3214，通过哈希函数，得出 3214 应该在 3 所对应的区块中。然后我们从 3 对应的区块中继续搜索，但并没有找到对应值，则说明 3214 不在哈希表中。

1.2 哈希函数

哈希函数：将哈希表中元素的键值(key)映射为元素存储位置(value)的函数。

哈希函数的重要的部分：

• 哈希函数应该易于计算，并且尽量使计算出来的索引值均匀分布。
• 哈希函数计算得到的哈希值是一个固定长度的输出值。
• if Hash(key1) != Hash(key2) 则 key1与key2一定不相等。
• if Hash(key1) = Hash(key2) 则key1与key2可能相等，也可能不相等（哈希碰撞）

下面我们介绍几个常用的哈希函数方法:

• 直接定值法：取关键字或者关键字的某个线性函数为哈希地址。即：Hash(key) = a*key + b,其中a和b为常熟。

这种计算最为简单，且不会产生哈希碰撞。适用于关键字分布基本连续的情况，如果关键字分布不连续，空位较多，则会造成存储空间的浪费。

• 除留余数法：假设哈希表的表长为m，取一个不大于m但接近或等于m的质数p，利用取模运算，将关键字转换为哈希地址。即：Hash(key) = key % p，其中p为不大于m的质数。

这也是一种简单且常用的哈希函数方法。其关键点在于 p 的选择。根据经验而言，一般 p 取素数或者 m，这样可以尽可能的减少冲突。

• 平方取中法：先通过求关键字平均值的方式扩大相近数之间的差别，然后根据表长度取关键字平方值的中间几位数为哈希地址。
  比如：Hash(key) = (key * key) // 100 % 1000，先计算平方，去除末尾的 2 位数，再取中间 3 位数作为哈希地址。

这种方法因为关键字平方值的中间几位数和原关键字的每一位数都相关，所以产生的哈希地址也比较均匀，有利于减少冲突的发生。

• 基数转换法：将关键字看成另一种进制的数再转换成原来进制的数，然后选其中几位作为哈希地址。
  比如：将关键字看做是 13 进制的数，再将其转变为 10 进制的数，将其作为哈希地址。

1.3 哈希冲突

哈希冲突（Hash Collision）：不同的关键字通过同一个哈希函数可能得到同一哈希地址，即 key1 ≠ key2，而 Hash(key1) = Hash(key2)，这种现象称为哈希冲突。

常用的哈希冲突解决方法主要是两类：「开放地址法（Open Addressing）」 和 「链地址法（Chaining）」。

1.3.1 开放地址法

开放地址法（Open Addressing）：是指当发生地址冲突时，按照某种方法继续探测哈希表中的其他存储单元，直到找到空位置为止。

当发生冲突时，开放地址法按照下面的方法求得后继哈希地址：
H(i) = (Hash(key) + F(i)) % m，i = 1, 2, 3, …, n (n ≤ m - 1)

• H(i) 是在处理冲突中得到的地址序列。即在第 1 次冲突（i = 1）时经过处理得到一个新地址 H(1)，如果在 H(1) 处仍然发生冲突（i = 2）时经过处理时得到另一个新地址 H(2) …… 如此下去，直到求得的 H(n) 不再发生冲突。
• Hash(key) 是哈希函数，m 是哈希表表长，对哈希表长取余的目的是为了使得到的下一个地址一定落在哈希表中。
• F(i) 是冲突解决方法，取法可以有以下几种：
  线性探测法：逐渐查询是否存在空地址
  
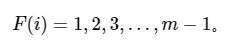
  二次探测：
  
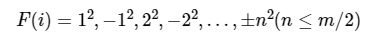
  伪随机数序列：
  

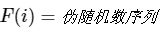
1.3.2 链地址法：

**链地址法（Chaining）：**将具有相同哈希地址的元素（或记录）存储在同一个线性链表中。

链地址法是一种更加常用的哈希冲突解决方法。相比于开放地址法，链地址法更加简单。

假设哈希函数产生的哈希地址区间为 [0, m - 1]，哈希表的表长为 m。则可以将哈希表定义为一个有 m 个头节点组成的链表指针数组 T。就是凡是哈希地址为i的元素都插入到同一个链表中，元素插入的位置可以是表头（头插法），也可以是表尾（尾插法）

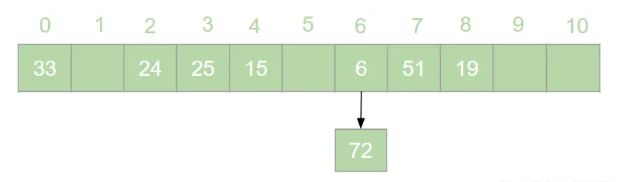
例如：[19,24,6,33,51,15,25,72] ，使用除留取余法：f(key)=key % 11，以余数作为该元素在数组中的存储的位置。则会得到一个如下图所示的哈希表：

当插入72时，发生冲突，Hash(6)=6，即6位置本身已经存有元素，但是Hash(72)=6，此时发生冲突，则按照链地址法将冲突的元素以链表的形式挂在后面，如下图

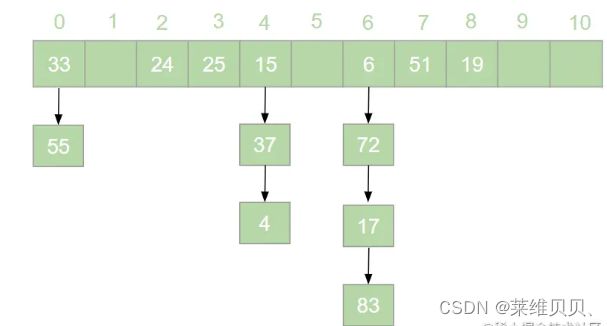
我们可以向这组数据中再添加一些元素，得到一组新的数据
[19,24,6,33,51,15,25,72,37,17,4,55,83]。使用链地址法得到如下哈希表：

1.4 哈希总结：

哈希表：通过键key和一个映射函数Hash(key)计算出对应的值value，把关键码值映射到表中一个位置来访问记录，以加快查找速度。
哈希函数：将哈希表中元素的关键键值映射为元素存储位置的函数。
哈希冲突：不同的关键字通过同一个哈希函数可能得到同一个哈希地址

「哈希函数的构建」：直接定址法、除留余数法、平方取中法、基数转换法、数字分析法、折叠法、随机数法、乘积法、点积法等。
「哈希冲突的解决方法」：开放地址法和链地址法等。

2.哈希表的应用案列

2.1 案例一：705. 设计哈希集合

705. 设计哈希集合

class MyHashSet:

    def __init__(self):
        self.set = [False] * 1000001

    def add(self, key):
        self.set[key] = True

    def remove(self, key):
        self.set[key] = False

    def contains(self, key):
        return self.set[key]

参考：

• https://algo.itcharge.cn
• 【博文】 哈希算法及 python 字典的实现 – Tim’s Path
• 【文章】 哈希表 - LeetBook - 力扣（LeetCode）
• 【文章】 漫画算法 - 小灰的算法之旅 - LeetBook - 力扣（LeetCode）
• 【博文】 面试官：哈希表都不知道，你是怎么看懂 HashMap 的？ 掘金
• 【博文】 散列表（上）- 数据结构与算法之美 - 极客时间