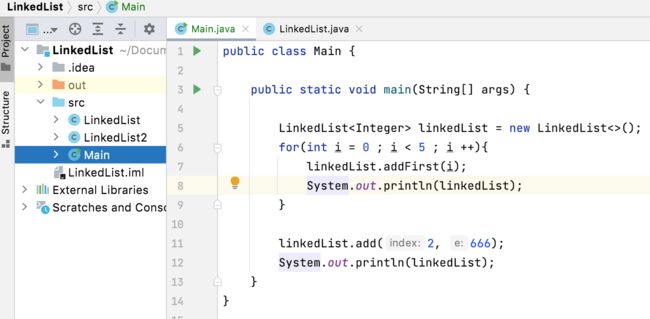
接着上一次https://www.cnblogs.com/webor2006/p/15195969.html的数据结构继续往下学习,这次会进入一个非常重要的数据结构的学习----链表,这个是未来学习复杂算法的一个基础,大量会被用到,所以,先夯实好基础。
什么是链表?
对于链表这个数据结构,应该人人都有所了解,为了学习成体系,还是再来简单审视一下它。
线性数据结构:
在前面,咱们已经学习了这三种线性的数据结构:
- 动态数组:https://www.cnblogs.com/webor2006/p/14092866.html
- 栈:https://www.cnblogs.com/webor2006/p/14216904.html
- 队列:https://www.cnblogs.com/webor2006/p/14216904.html
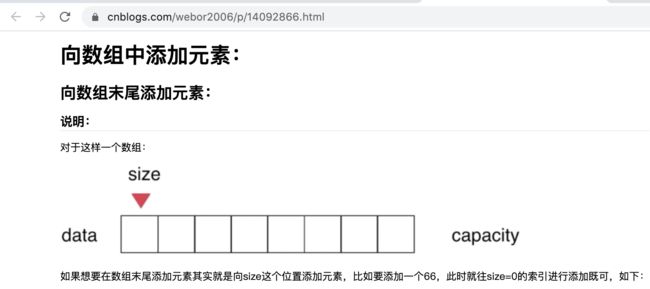
对于这三种数据结构,其实它底层都是依托“静态”数组来实现的,而我们使用时感觉是动态的是因为靠resize解决固定容量的问题,拿动态数组的底层实现为例:
也就是说其实它是一个“假”的动态,但是!!!对于今天学习的另一个线性数据结构---链表,它就不一样了,它是真正的动态数据结构,关于它的动态在之后的使用中再来慢慢体会。
为什么链表很重要?
对于链表来说它是数据结构的一个重点,那为啥它这么重要呢?主要有以下几点原因:
-
最简单的动态数据结构:
在之后还会接触到更多的动态数据结构,比如二分搜索树、平衡二叉树(AVL、红黑树),而学好这些更高级的动态数据结构的前提就是学好链表。 -
更深入的理解引用(或者指针):
这个是跟内存相关的,虽然在Java不需要手动管理内存,但是!!!对链表这种数据结构更加深入的理解,可以帮忙我们对于引用、指针,甚至计算机系统和内存管理相关的很多话题有更深入的认识。 -
更深入的理解递归【这个是一个非常有意义的点】:
就在上周学习的关于Android UI相关的这篇https://www.cnblogs.com/webor2006/p/12901271.html中就用到了使用递归来解决通用贝塞尔曲线的画法,当时说实话对于它的实现还是很难理解的,那如果你学好的链表,是能让你更深入的去理解递归的,因为链表本身是有非常清晰的递归结构的,只是过链表这种数据结构它是一种线性的,所以通常会比较容易使用循环的方式来操作链表,但是!!!由于链表天生就具有递归结构的性质的,所以学好链表是可以让你更加深入的理解递归的,而学好递归也是未来学习更加复杂的树型结构必备的基础。 -
辅助组成其他数据结构:
比如图结构、Hash表数据结构、还有用链表也可以实现栈和队列,一句话,学好链表,是让你在未来学习更高级的数据结构的基础。
了解链表:
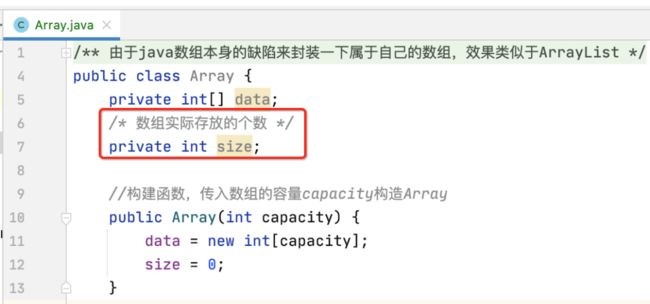
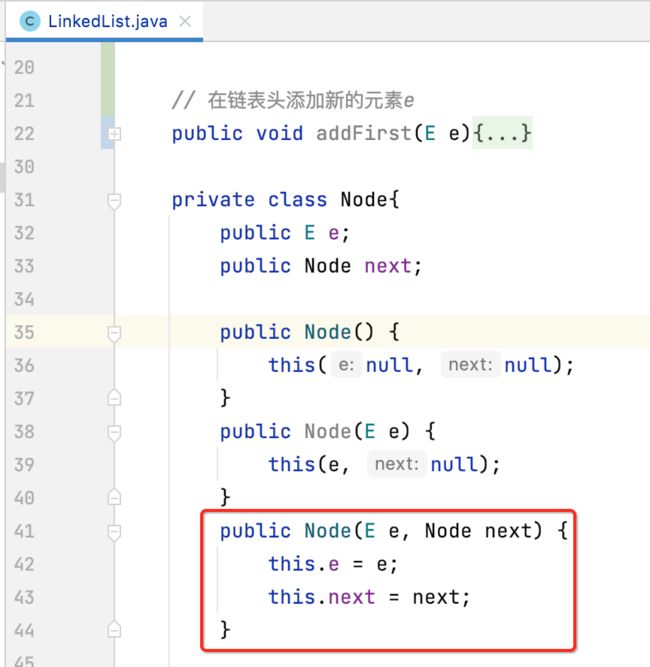
接下来再直观的了解一下链表,由于基本上每个人对它都有所了解,简单过一下,用一句话来描述它就是:“数据存储在"节点"(Node)中”, 如何理解?看一下代码就知道了:
而举个使用这个结构的例子,整个链表就长这样:
其中标志着链表的结束是它的next指向了一个NULL了。
优缺点:
对于链表的优缺点应该也是人人皆知的了,不过这里重点要理解的就是“动态”这个词,下面再来提一下它的这两个点。
优点:
真正的动态,不需要处理固定容量的问题。对比着静态数组来理解这个“动态”,像静态数组是一下子就要new出来一片空间,还得考虑空间是否不够用、开多了浪费之类的问题对吧?而对于链表来说,你需要存储多少个数据就可以生成多少个结点把它们挂接起来,这就是所谓“动态”的含义。
缺点:
丧失了随机访问的能力,这块特性就不过多说明了,链表是不能像数组那样通过索引下标直接访问的,究其原因是因为数组开辟的内存空间是连续的,很方便通过索引来直接访问,而链表由于是靠next一层层进行连接,对于每一个节点所在的内存位置是不同的,只能通过next一点点来查找我们需要查找的元素。
数组和链表的对比:
通过上面对链表的优缺点的描述,我们也很容易地总结出数组和链表的使用场景。
在链表中添加元素:
定义链表数据结构:
既然是要在链表中添加元素,肯定得要有一个链表的数据结构Node对吧,所以先来定义一下:
其中Node结构的定义比较简单,直接给出了:
public class LinkedList {
private class Node{
public E e;
public Node next;
public Node() {
this(null, null);
}
public Node(E e) {
this(e, null);
}
public Node(E e, Node next) {
this.e = e;
this.next = next;
}
@Override
public String toString() {
return e.toString();
}
}
}
其中使用了泛型可以承载任何数据。
定义基础成员变量:
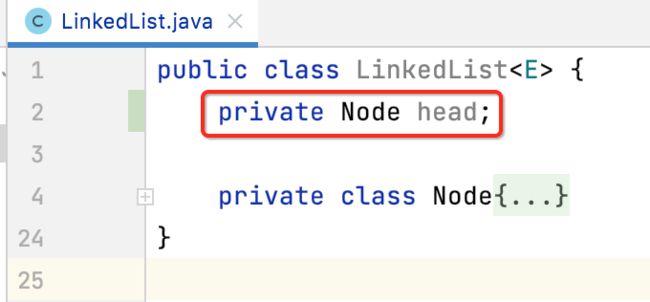
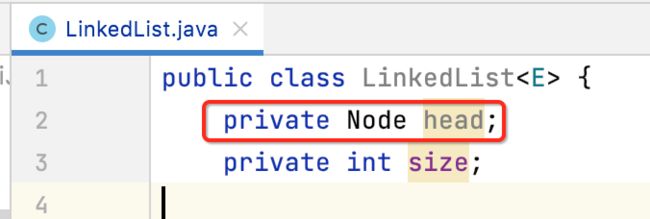
head:链表头结点
对于链表来说,为了方便访问,是需要存储一个链表的头的:
所以咱们定义一下:
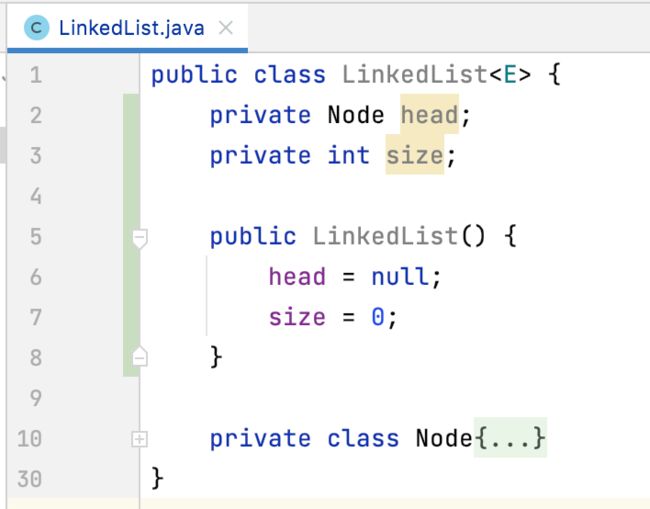
size:链表的元素个数
这个不用多说,肯定是有获取整个链表元素个数的场景的:
定义默认构造:
其实可以不用定义,这里显示的再定义一下。
定义两个辅助方法:
添加元素:
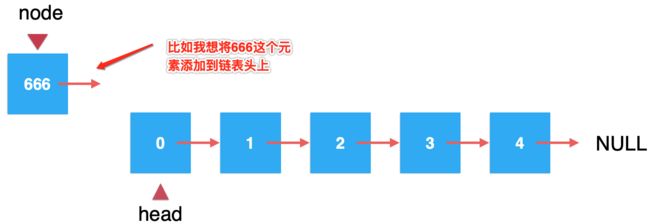
在链表头添加元素:
这是因为对于数组这样的数据结构往数组尾添加一个元素是最方便的,而对于链表来说,在添加数据方面恰恰跟数组添加是相反的,在链表头添加是最方便的。其实也很好理解,因为在数组中有size这个变量在跟踪数组最后一个元素的下一个待添加的位置,固然往尾部添加很容易:
但是在链表中虽然我们也有size这个变量,但是它只是表示元素的总个数,不会跟踪链表的最后一个元素的位置的,但是它里面也有一个跟踪位置的变量那就是head,用来跟踪链表头:
对于链表来说头添加元素是很方便的。
思路:
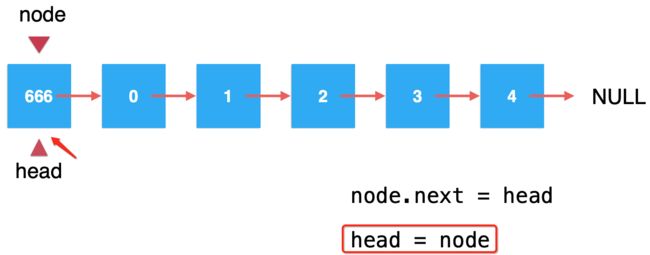
此时我们只需要让"node.next=head"是不是就将其放到链表头了?也就是:
但是还差一步,就是需要将head指向为添加的这个666元素:
而这整个过程肯定是在一个方法中执行的对吧,那么对于node这个方法中的局部变量肯定会被销毁的,最后的形态就是:
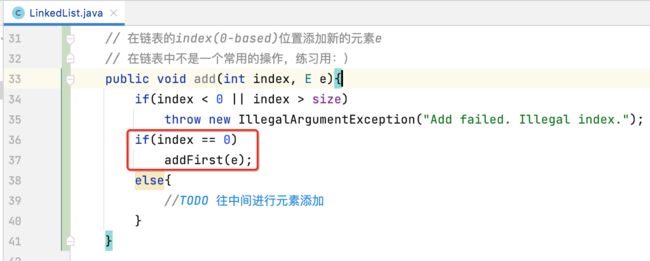
实现:
有了上面的思路,实现起来当然非常之简单啦,如下:
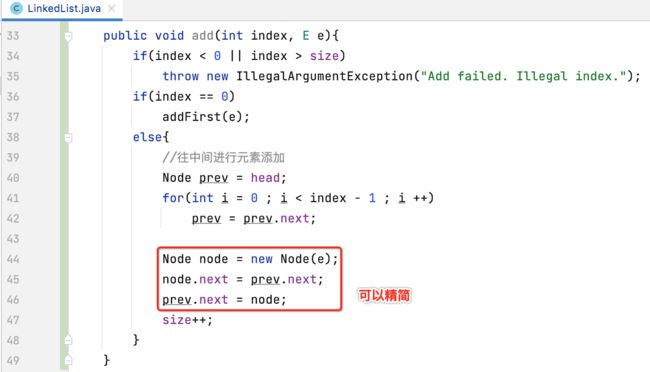
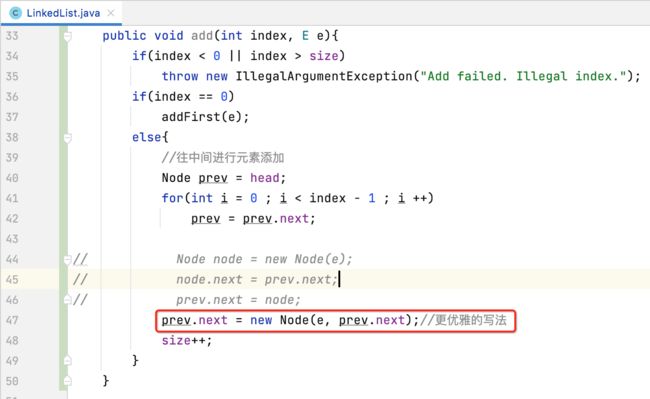
不过,这里的代码是可以优化的,让其变得更加的优雅精练,如下:
因为咱们定义的这个构造方法:
就是来干这两行代码所干的事的:
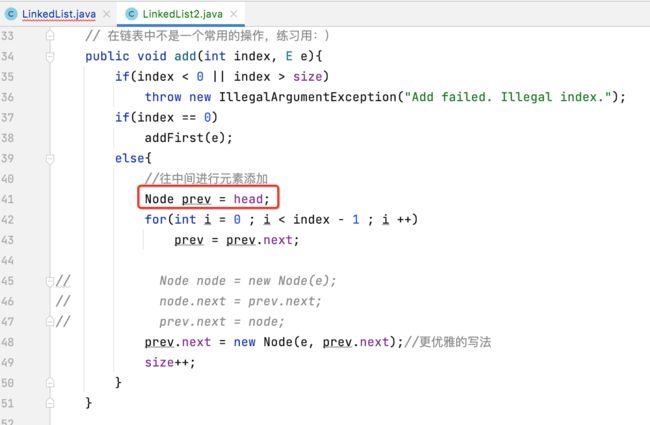
在链表中间添加元素:
思路:
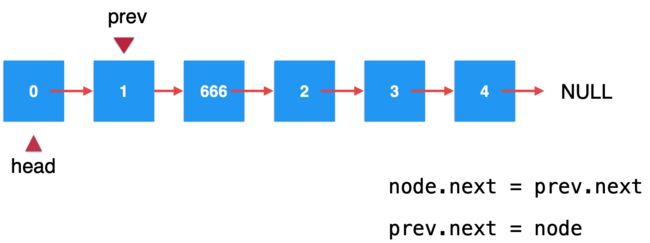
然后在索引为2的地方添加元素666,也就是将它添加到元素1后面:
下面来看一下整个添加的过程:
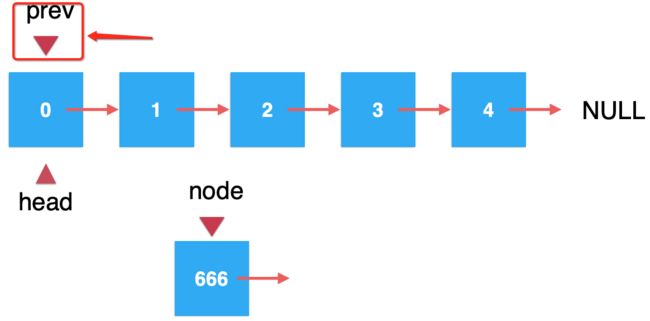
1、创建一个node结点:
2、找到指定待插入的结点:
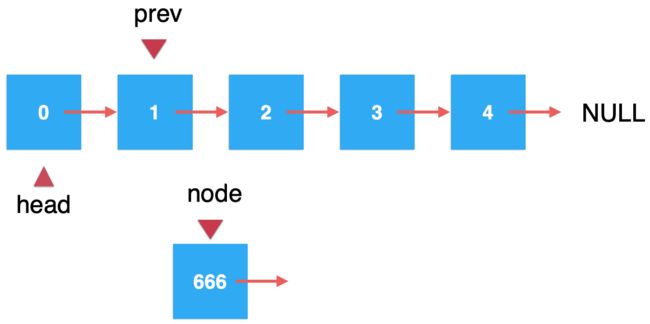
既然要将其插入到索引为2的位置,那很明显总得找到它之前索引为1的那们结点才可以,所以,这里将要查找的这个结点叫prev:
默认是指向链表头结点的,然后我们得找到索引为1的位置,那就从头往下遍历来找,由于下一个就是索引为1的结点,这里只需查找一次:
当然如果你要插入的位置比较靠后,那遍历的时间就要长一点。
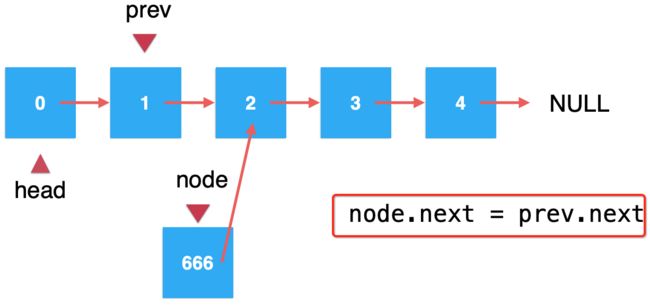
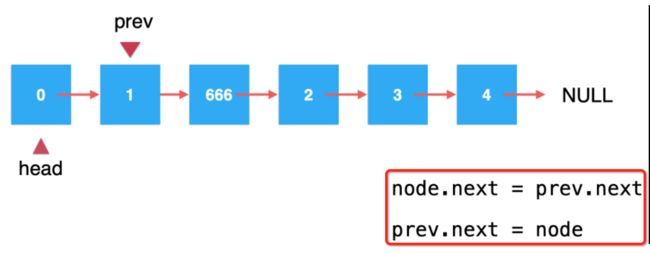
3、将待插入的元素它的下一个结点指向prev.next:
直接看图说话:
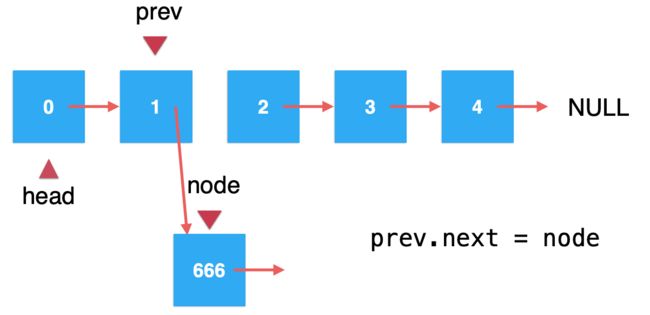
4、将node作为prev的next的引用:
这样就成功的将666元素插入到了索引为1的位置了:
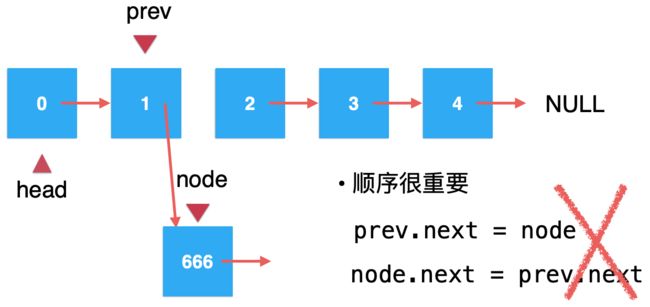
注意点!!!
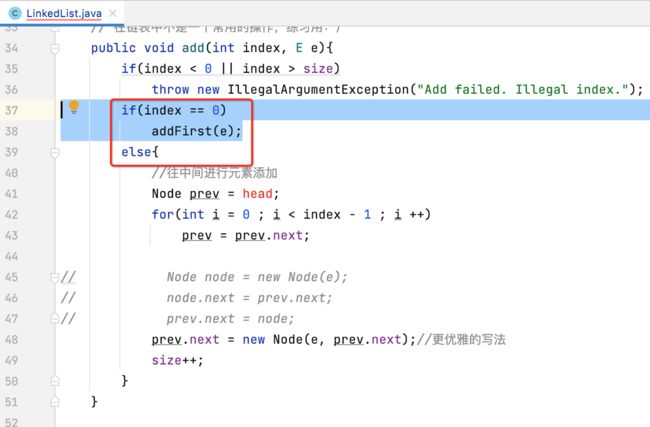
综上所述,其实添加的关键点是找到要添加的节点的前一个节点对吧,在正式实现之前,这里还有一个注意点需要说明一下,也是非常容易犯错的,那就是在添加元素时,目前我们的代码是这么写的对吧:
那我能否将这两句代码的顺序颠倒一下,也就是变成它?
实现:
使用链表的虚拟头结点:
产生的背景:
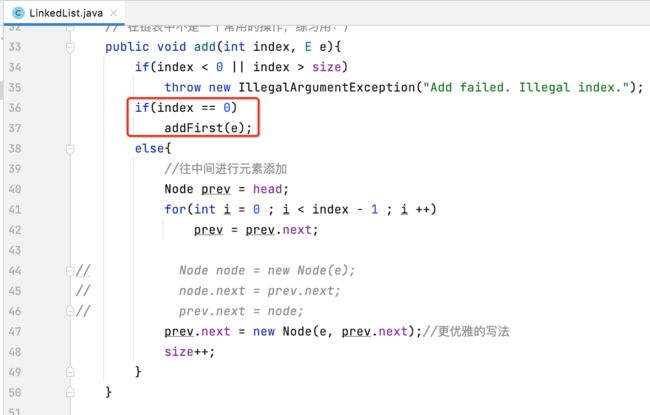
在上面往指定索引添加元素的方法实现中,有一个不太优雅的地方,就是需要判断待插入的位置是否是头结点的位置:
之所在多出这么一个判断,是因为头结点是没有prev结点的,那很明显就无法使用这段逻辑统一来完成了:
貌似理解很正常呀,这有啥值得提的呢?值得,因为有办法让咱们的代码更加的精简,什么办法?在链表具体实现的过程中,有一个非常常用的技巧可以把链表头这种特殊的操作跟其它结点的操作给统一起来,也就是如标题所示,设置虚拟头结点。也就是:
然后我们将这个null结点称之为dummyHead,dummy的含义:
也就是:
要注意:dumyHead这个位置的元素是根本不存在的,对于用户来讲也根本木有意义的,只是为了咱们编写逻辑方便出现的一个虚拟的头结点,也就是为了我们逻辑编写的方便多浪费了一个空间,跟之前https://www.cnblogs.com/webor2006/p/14216904.html学习时实现的循环队列时也浪费一个空间一样的思想:
那有了这个虚拟头结点之后,对于咱们往指定索引添加元素时,就会产生一个非常好的效应,对于用户传来要插入索引为0位置的元素时,依然可以找到prev结点,此时就是咱们设置的dummyHead,那么咱们就可以减少对头结点特殊处理的条件了,让整个方法的实现都是一个统一的逻辑。
链表加入虚拟头结点:
1、定义dummyHead:
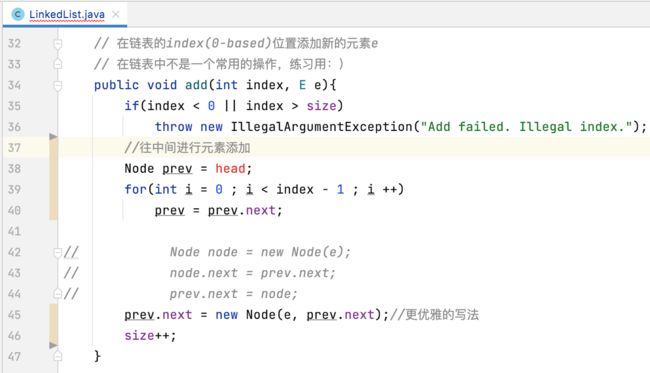
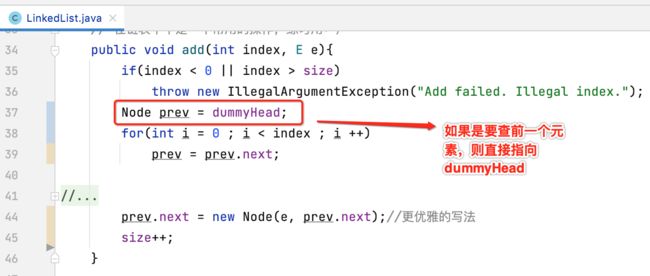
2、改造add()方法:
有了虚拟头结点之后,这块的条件就可以去掉了:
然后具体的改造如下:
另外,这个条件也得改一下:
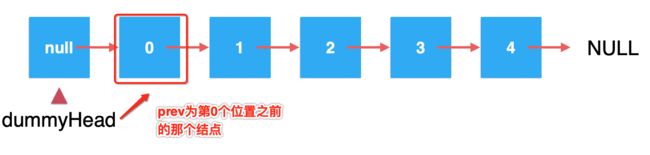
关于这块改造,如有模糊的,可以对着图画一画就清楚了,因为相比之前,我们此时默认prev是指向了第0个元素的前一个结点了:
那如果我想在索引为2的位置进行元素插入,是不是得刚好遍历两次,此时的prev就指向了元素1,也就是要插入索引2位置之前的那一个结点了?而在之前咱们的实现是默认指向的第一个结点:
那要找到指定位置很明显要遍历index-1次了,一定要明白改造的背后含义。至此,咱们的add方法就没有针对头结点进行特殊处理,而都是一个通用的处理了,是不是代码更加的优雅?有了这个虚拟头结点之后,在之后链表的实现中也就更加的便捷了。
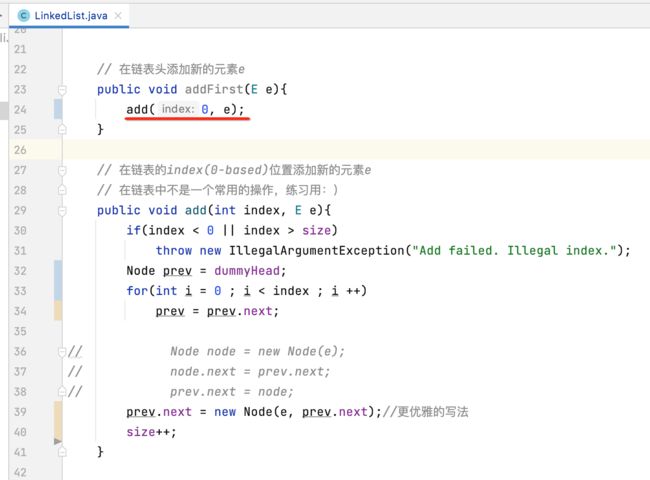
3、改造addFirst()方法:
目前还有一处报错:
关于这块,咱们就可以直接利用add()方法来实现了,如下:
最后调整一下代码的顺序,让其更加可读:
链表的遍历,查询和修改:
遍历查询:
接下来则来往链表中添加查询相关的方法,没有复杂的逻辑,直接快速过一下。
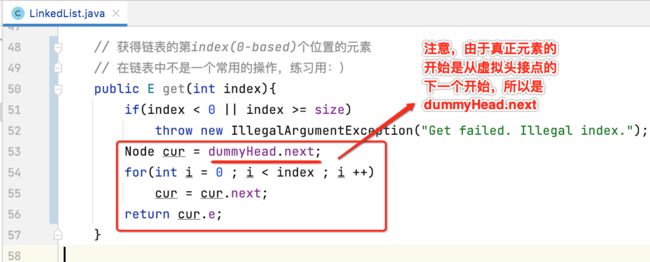
get(int index):获得链表的第index(0-based)个位置的元素
1、检查索引的合法性:
2、开启遍历:
这里注意一下遍历跟插入元素时遍历的细节:
而如果是遍历元素,则需要从dummyHead.next开始,
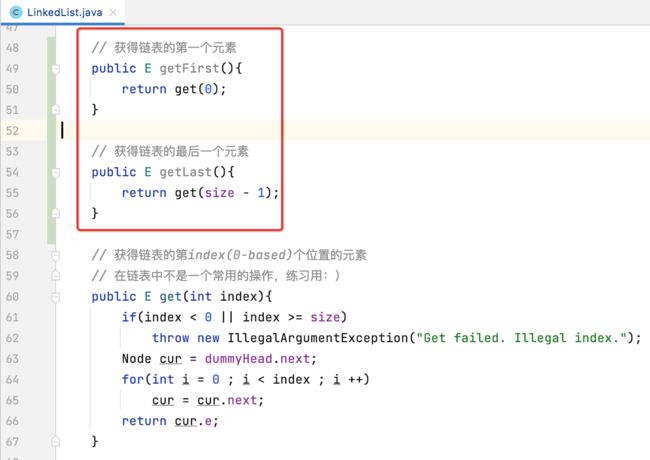
getFirst()、getLast():
有了get()方法,就可以给用户添加两个便捷方法:
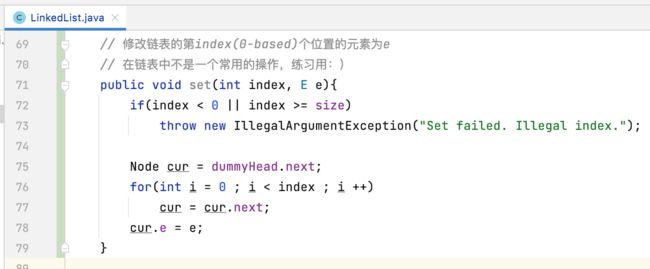
修改:
对于更新方法也比较简单,直接贴出代码:
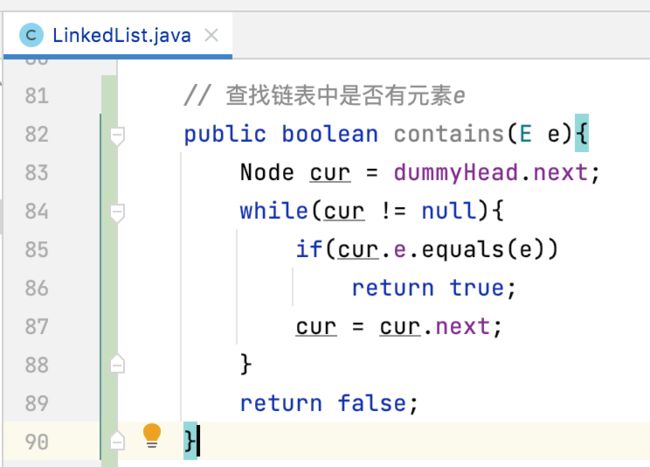
查找链表中是否有元素e:
接下来再来封装一个判断元素是否在链表中的方法,也是很简单,不过多说明:
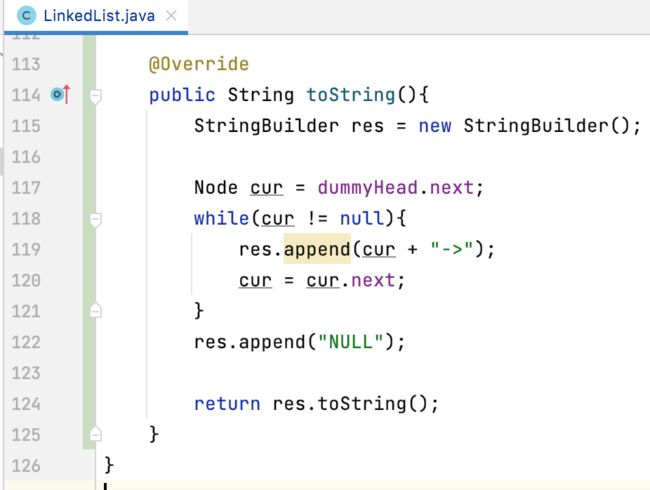
toString():
为了方便观察链表元素的情况,重写一下toString():
其中遍历还可以改用for循环来,这里练习一下:
运行:
最后,咱们来针对目前已经实现的方法进行一个测试,整个实现其实都不难【之后对于链表还有很多知识需要拓展,慢慢来,先打基础】,但是呢又不能不过一遍,当复习吧,测试代码如下:
运行结果:
从链表中删除元素:
思路:
接下来还差从链表中删除元素的功能, 由于这个删除操作稍复杂一些,在正式实现之前,同样先来了解整个思路,比如有这么一个链表,带虚拟头结点:
假如我们想删除索引为2位置的元素,具体的过程如下:
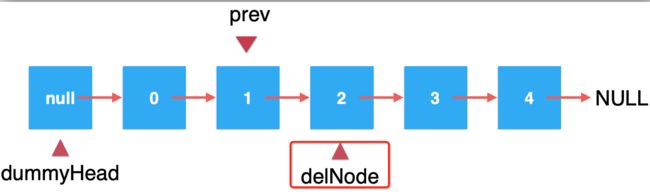
跟添加一样,也需要找到prev结点:
这样就开始遍历,直到找到它:
然后标记出来我们要删除的元素:
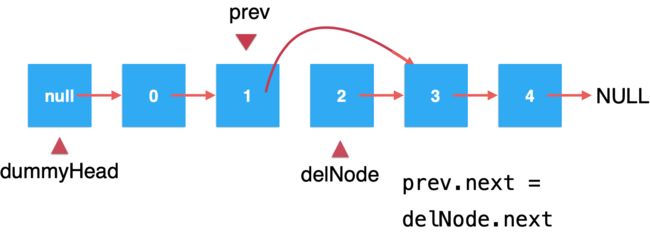
接下来是不是得让prev.next=delNode.next?如下:
然后为了让GC能回收delNode,需要再将delNode.next=null,如下:
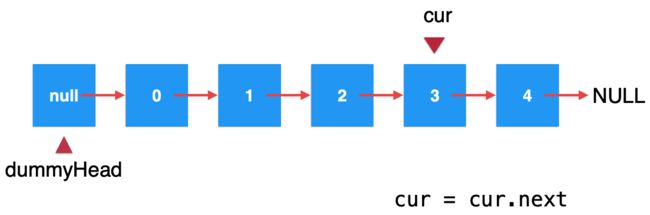
链表元素删除常⻅的错误:
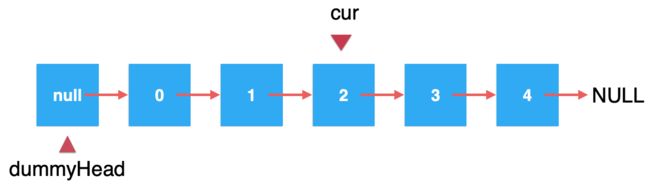
在正式实现删除方法之前,针对一个很容易犯的一个错误进行说明,以便我们好规避这个坑。这个坑是这样的,既然我是要删除那个元素,那么好,我先遍历找到待删除的元素:
这里还是以删除2为例:当找到待删除的元素:
然后我执行“cur = cur.next”,这样就好了呀,你仔细分析一下,经过这样执行之后,其实就是改变了cur的位置了,对于整个链表关系是没有发生任何变化的,如下:
所以,这一点需要注意,不过犯这种低级错误的应该不多,毕竟对于链表这种常见的数据结构都比较了解。
实现:
有了思路之后,实现就不难了。
removeElement(E e):
这里直接给出实现,比较好理解:
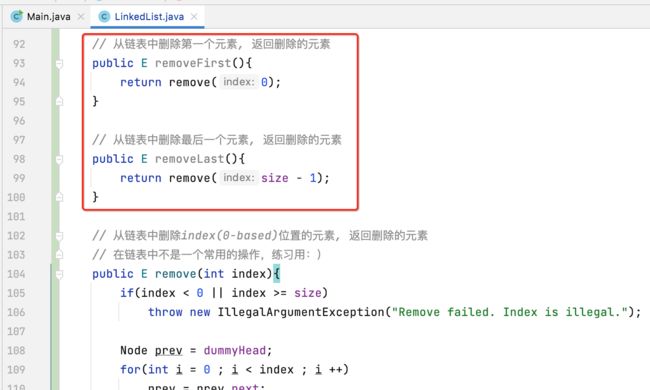
removeFirst()、removeLast():
有了remove方法之后,同样可能提供两个删除首尾元素的便捷方法:
removeElement(E e):
有时候可能会删除指定的结点,实现也很简单:
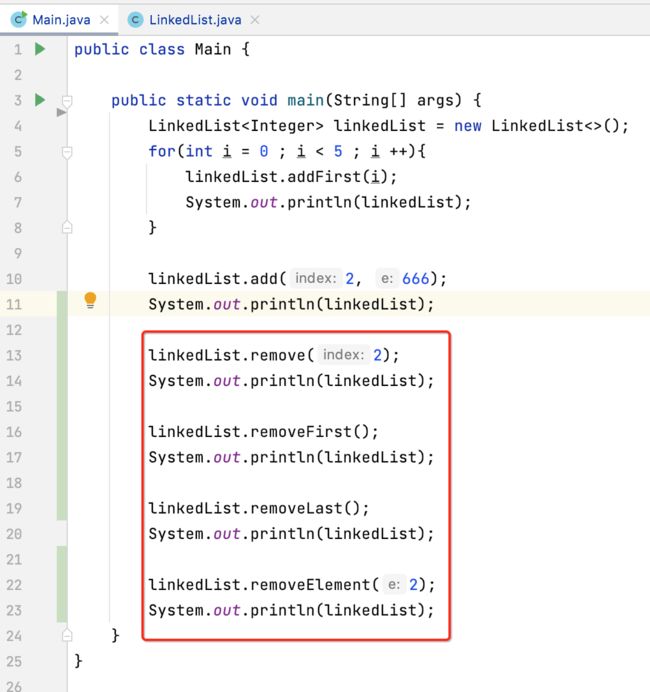
测试:
接下来咱们来测试一下:
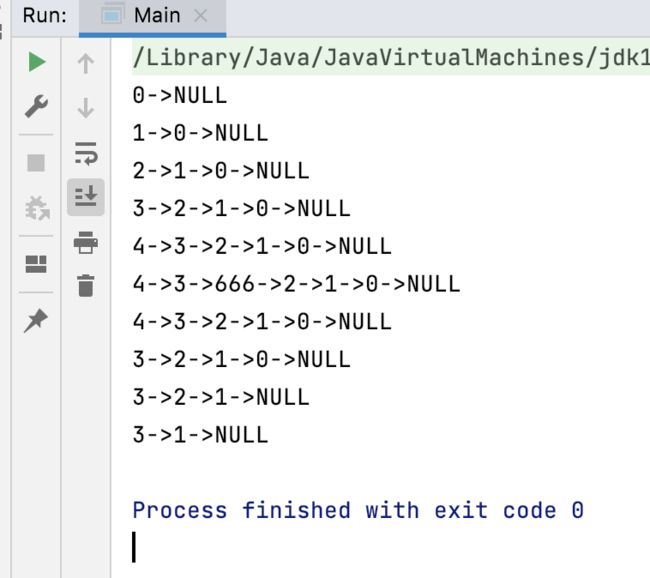
运行结果:
时间复杂度分析:
先来将目前实现的整个链表的代码贴一下:
//带虚拟头结点的版本
public class LinkedList {
private Node dummyHead;//虚拟头结点
private int size;
public LinkedList() {
dummyHead = new Node();
size = 0;
}
// 获取链表中的元素个数
public int getSize(){
return size;
}
// 返回链表是否为空
public boolean isEmpty(){
return size == 0;
}
// 在链表头添加新的元素e
public void addFirst(E e){
add(0, e);
}
// 在链表末尾添加新的元素e
public void addLast(E e){
add(size, e);
}
// 在链表的index(0-based)位置添加新的元素e
// 在链表中不是一个常用的操作,练习用:)
public void add(int index, E e){
if(index < 0 || index > size)
throw new IllegalArgumentException("Add failed. Illegal index.");
Node prev = dummyHead;
for(int i = 0 ; i < index ; i ++)
prev = prev.next;
// Node node = new Node(e);
// node.next = prev.next;
// prev.next = node;
prev.next = new Node(e, prev.next);//更优雅的写法
size++;
}
// 获得链表的第一个元素
public E getFirst(){
return get(0);
}
// 获得链表的最后一个元素
public E getLast(){
return get(size - 1);
}
// 获得链表的第index(0-based)个位置的元素
// 在链表中不是一个常用的操作,练习用:)
public E get(int index){
if(index < 0 || index >= size)
throw new IllegalArgumentException("Get failed. Illegal index.");
Node cur = dummyHead.next;
for(int i = 0 ; i < index ; i ++)
cur = cur.next;
return cur.e;
}
// 修改链表的第index(0-based)个位置的元素为e
// 在链表中不是一个常用的操作,练习用:)
public void set(int index, E e){
if(index < 0 || index >= size)
throw new IllegalArgumentException("Set failed. Illegal index.");
Node cur = dummyHead.next;
for(int i = 0 ; i < index ; i ++)
cur = cur.next;
cur.e = e;
}
// 查找链表中是否有元素e
public boolean contains(E e){
Node cur = dummyHead.next;
while(cur != null){
if(cur.e.equals(e))
return true;
cur = cur.next;
}
return false;
}
// 从链表中删除第一个元素, 返回删除的元素
public E removeFirst(){
return remove(0);
}
// 从链表中删除最后一个元素, 返回删除的元素
public E removeLast(){
return remove(size - 1);
}
// 从链表中删除index(0-based)位置的元素, 返回删除的元素
// 在链表中不是一个常用的操作,练习用:)
public E remove(int index){
if(index < 0 || index >= size)
throw new IllegalArgumentException("Remove failed. Index is illegal.");
Node prev = dummyHead;
for(int i = 0 ; i < index ; i ++)
prev = prev.next;
Node retNode = prev.next;
prev.next = retNode.next;
retNode.next = null;
size --;
return retNode.e;
}
// 从链表中删除元素e
public void removeElement(E e){
Node prev = dummyHead;
while(prev.next != null){
if(prev.next.e.equals(e))
break;
prev = prev.next;
}
if(prev.next != null){
Node delNode = prev.next;
prev.next = delNode.next;
delNode.next = null;
size --;
}
}
private class Node{
public E e;
public Node next;
public Node() {
this(null, null);
}
public Node(E e) {
this(e, null);
}
public Node(E e, Node next) {
this.e = e;
this.next = next;
}
@Override
public String toString() {
return e.toString();
}
}
@Override
public String toString(){
StringBuilder res = new StringBuilder();
//第一种遍历方法
// Node cur = dummyHead.next;
// while(cur != null){
// res.append(cur + "->");
// cur = cur.next;
// }
//第二种遍历方法
for(Node cur = dummyHead.next ; cur != null ; cur = cur.next)
res.append(cur + "->");
res.append("NULL");
return res.toString();
}
}
接下来分析一下各操作的复杂度。
添加操作:O(n)
addLast(e):O(n)
addFirst(e):O(1)
add(index, e):O(n/2) = O(n)
删除操作:O(n)
removeLast(e):O(n)
removeFirst(e):O(1)
remove(index, e):O(n/2) = O(n)
修改操作:O(n)
set(index, e):O(n)
查找操作:O(n)
get(index):O(n)
总结:
说实话,对于这次的链表的学习还是很简单的,但是简单不代表就可以忽视它,因为它是最基础的动态数据结构,只有学扎实了它,才能对后续学习更复杂的动态数据结构【比如让人生畏的红黑树】起到巨大的帮助,关于链表还有很多内容,待之后再继续。