【数据结构与算法】----二叉树

作者：旧梦拾遗186

专栏：数据结构成长日记

 

目录

1.树概念及结构

1.1树的概念

1.2 树的结构

1.3 树的表示 

1.4 树在实际中的运用（表示文件系统的目录树结构）  

2.二叉树概念及结构 

2.2现实中的二叉树： 

2.3 特殊的二叉树： 

2.4 二叉树的性质  

2.5 二叉树的存储结构

3.二叉树的顺序结构及实现

3.1 二叉树的顺序结构

3.2 堆的概念及结构  

3.3 堆的实现

Heap.h

Heap.c

---

1.树概念及结构

1.1树的概念

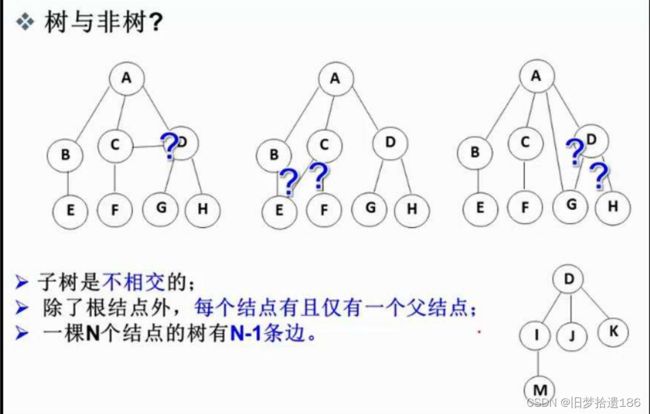
树是一种 非线性 的数据结构，它是由 n （ n>=0 ）个有限结点组成一个具有层次关系的集合。 把它叫做树是因 为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的 。

有一个 特殊的结点，称为根结点 ，根节点没有前驱结点

除根节点外， 其余结点被分成 M(M>0) 个互不相交的集合 T1 、 T2 、 …… 、 Tm ，其中每一个集合 Ti(1<= i <= m)又是一棵结构与树类似的子树。每棵子树的根结点有且只有一个前驱，可以有 0 个或多个后继

因此， 树是递归定义 的。

注意：树形结构中，子树之间不能有交集，否则就不是树形结构  

 

1.2 树的结构

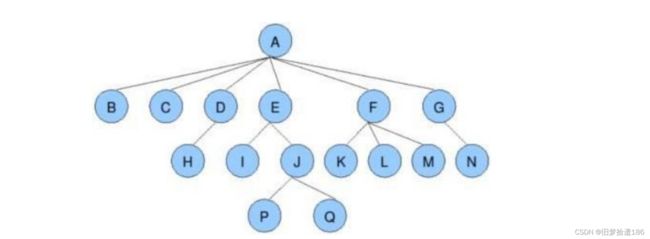
节点的度 ：一个节点含有的子树的个数称为该节点的度； 如上图： A 的为 6

叶节点或终端节点 ：度为 0 的节点称为叶节点； 如上图： B 、 C 、 H 、 I... 等节点为叶节点

非终端节点或分支节点 ：度不为 0 的节点； 如上图： D 、 E 、 F 、 G... 等节点为分支节点

双亲节点或父节点 ：若一个节点含有子节点，则这个节点称为其子节点的父节点； 如上图： A 是 B 的父节点

孩子节点或子节点 ：一个节点含有的子树的根节点称为该节点的子节点； 如上图： B 是 A 的孩子节点

兄弟节点 ：具有相同父节点的节点互称为兄弟节点； 如上图： B 、 C 是兄弟节点

树的度 ：一棵树中，最大的节点的度称为树的度； 如上图：树的度为 6

节点的层次 ：从根开始定义起，根为第 1 层，根的子节点为第 2 层，以此类推；

树的高度或深度 ：树中节点的最大层次； 如上图：树的高度为 4

堂兄弟节点 ：双亲在同一层的节点互为堂兄弟；如上图： H 、 I 互为兄弟节点

节点的祖先 ：从根到该节点所经分支上的所有节点；如上图： A 是所有节点的祖先

子孙 ：以某节点为根的子树中任一节点都称为该节点的子孙。如上图：所有节点都是 A 的子孙

森林 ：由 m （ m>0 ）棵互不相交的树的集合称为森林；

 

1.3 树的表示 

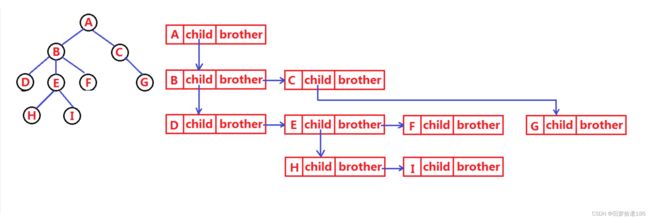
树结构相对线性表就比较复杂了，要存储表示起来就比较麻烦了， 既然保存值域，也要保存结点和结点之间 的关系 ，实际中树有很多种表示方式如：双亲表示法，孩子表示法、孩子双亲表示法以及孩子兄弟表示法 等。我们这里就简单的了解其中最常用的孩子兄弟表示法 。

 

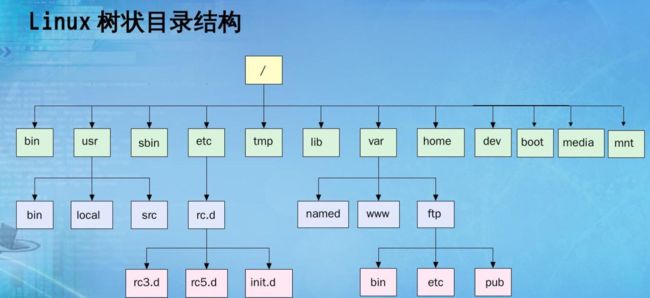
1.4 树在实际中的运用（表示文件系统的目录树结构）  

2.二叉树概念及结构 

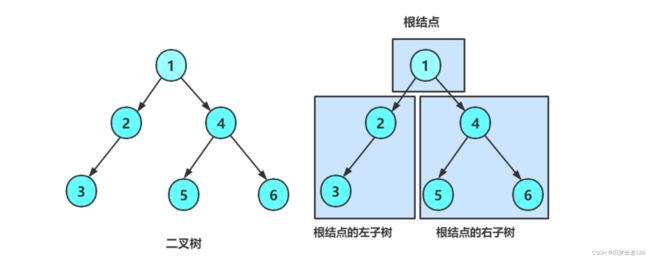
一棵二叉树是结点的一个有限集合，该集合 :

1. 或者为空

2. 由一个根节点加上两棵别称为左子树和右子树的二叉树组成

从上图可以看出：

1. 二叉树不存在度大于 2 的结点

2. 二叉树的子树有左右之分，次序不能颠倒，因此二叉树是有序树

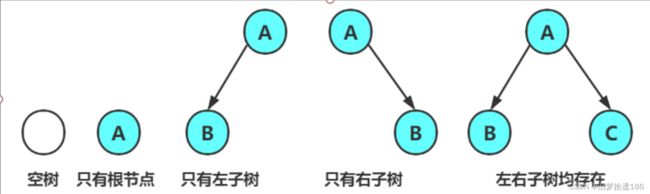
注意：对于任意的二叉树都是由以下几种情况复合而成的：

2.2现实中的二叉树： 

 

2.3 特殊的二叉树： 

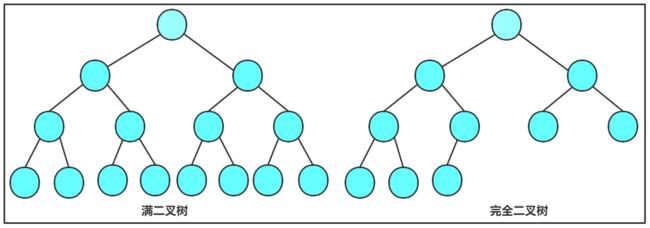
1. 满二叉树 ：一个二叉树，如果每一个层的结点数都达到最大值，则这个二叉树就是满二叉树。也就是 说，如果一个二叉树的层数为K ，且结点总数是 2^k-1，则它就是满二叉树。

2. 完全二叉树 ：完全二叉树是效率很高的数据结构，完全二叉树是由满二叉树而引出来的。对于深度为 K 的，有n 个结点的二叉树，当且仅当其每一个结点都与深度为 K 的满二叉树中编号从 1 至 n 的结点一一对 应时称之为完全二叉树。 要注意的是满二叉树是一种特殊的完全二叉树。

 

2.4 二叉树的性质  

 

1. 若 i>0 ， i 位置节点的双亲序号： (i-1)/2 ； i=0 ， i 为根节点编号，无双亲节点

2. 若 2i+1 ，左孩子序号： 2i+1 ， 2i+1>=n 否则无左孩子

3. 若 2i+2 ，右孩子序号： 2i+2 ， 2i+2>=n 否则无右孩子

题目练习：

1. 某二叉树共有 399 个结点，其中有 199 个度为 2 的结点，则该二叉树中的叶子结点数为（ ）

A 不存在这样的二叉树

B 200

C 198

D 199

2. 下列数据结构中，不适合采用顺序存储结构的是（ ）

A 非完全二叉树

B 堆

C 队列

D 栈

3. 在具有 2n 个结点的完全二叉树中，叶子结点个数为（ ）

A n

B n+1

C n-1

D n/2

4. 一棵完全二叉树的节点数位为 531 个，那么这棵树的高度为（ ）

A 11

B 10

C 8

D 12

5. 一个具有 767 个节点的完全二叉树，其叶子节点个数为（）

A 383

B 384

C 385

D 386

答案：

1.B

2.A

3.A

4.B

5.B

2.5 二叉树的存储结构

二叉树一般可以使用两种结构存储，一种顺序结构，一种链式结构。

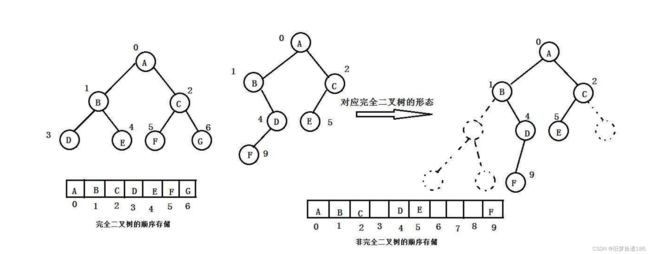
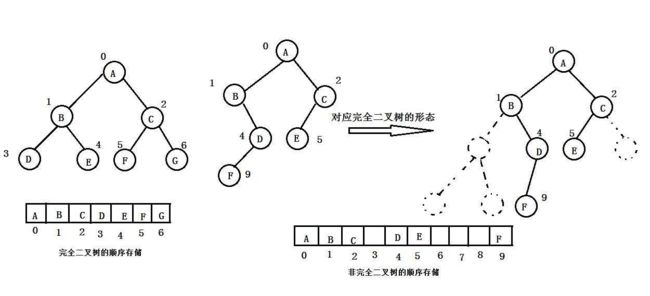
1. 顺序存储

顺序结构存储就是使用 数组来存储 ，一般使用数组 只适合表示完全二叉树 ，因为不是完全二叉树会有空

间的浪费。而现实中使用中只有堆才会使用数组来存储，关于堆我们后面的章节会专门讲解。 二叉树顺

序存储在物理上是一个数组，在逻辑上是一颗二叉树。

2. 链式存储

二叉树的链式存储结构是指，用链表来表示一棵二叉树，即用链来指示元素的逻辑关系。 通常的方法是 链表中每个结点由三个域组成，数据域和左右指针域，左右指针分别用来给出该结点左孩子和右孩子所 在的链结点的存储地址 。链式结构又分为二叉链和三叉链，当前我们学习中一般都是二叉链，后面课程 学到高阶数据结构如红黑树等会用到三叉链。

3.二叉树的顺序结构及实现

3.1 二叉树的顺序结构

普通的二叉树是不适合用数组来存储的，因为可能会存在大量的空间浪费。而完全二叉树更适合使用顺序结

构存储。 现实中我们通常把堆 ( 一种二叉树 ) 使用顺序结构的数组来存储，需要注意的是这里的堆和操作系统

虚拟进程地址空间中的堆是两回事，一个是数据结构，一个是操作系统中管理内存的一块区域分段。

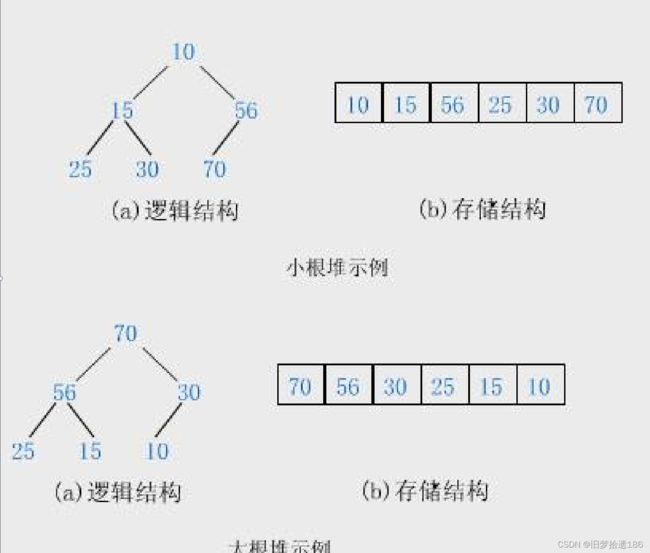
3.2 堆的概念及结构  

 

 

选择题

1. 下列关键字序列为堆的是：（）

A 100 , 60 , 70 , 50 , 32 , 65

B 60 , 70 , 65 , 50 , 32 , 100

C 65 , 100 , 70 , 32 , 50 , 60

D 70 , 65 , 100 , 32 , 50 , 60

E 32 , 50 , 100 , 70 , 65 , 60

F 50 , 100 , 70 , 65 , 60 , 32

2. 已知小根堆为 8 , 15 , 10 , 21 , 34 , 16 , 12 ，删除关键字 8 之后需重建堆，在此过程中，关键字之间的比较次

数是（）。

A 1

B 2

C 3

D 4

3. 一组记录排序码为 ( 5 11 7 2 3 17 ), 则利用堆排序方法建立的初始堆为

A ( 11 5 7 2 3 17 )

B ( 11 5 7 2 17 3 )

C ( 17 11 7 2 3 5 )

D ( 17 11 7 5 3 2 )

E ( 17 7 11 3 5 2 )

F ( 17 7 11 3 2 5 )

4. 最小堆 [ 0 , 3 , 2 , 5 , 7 , 4 , 6 , 8 ], 在删除堆顶元素 0 之后，其结果是（）

A [ 3 ， 2 ， 5 ， 7 ， 4 ， 6 ， 8 ]

B [ 2 ， 3 ， 5 ， 7 ， 4 ， 6 ， 8 ]

C [ 2 ， 3 ， 4 ， 5 ， 7 ， 8 ， 6 ]

D [ 2 ， 3 ， 4 ， 5 ， 6 ， 7 ， 8 ]

选择题答案

1. A

2. C

3. C

4. C

3.3 堆的实现

Heap.h

#define  _CRT_SECURE_NO_WARNINGS 1


#include
#include
#include
#include
#include


typedef int HPDataType;
typedef struct Heap
{
	HPDataType* a;
	int size;
	int capacity;
}HP;


//堆的初始化
void HeaPInit(HP* php);
//返回栈顶元素
HPDataType HeapTop(HP* php);
//判断是否为空
bool HeapEmpty(HP* php);
//插入x继续保持堆的形态
void HeapPush(HP* php, HPDataType x);
//打印堆
void HeapPrint(HP* php);
//元素个数
int HeapSize(HP* php);
//返回堆顶元素
HPDataType HeapTop(HP* php);
//删除堆顶元素——找出次大或者次小
void HeapPop(HP* php);

Heap.c

#define  _CRT_SECURE_NO_WARNINGS 1
#include"Heap.h"
//堆的初始化
void HeaPInit(HP* php)
{
	assert(php);
	php->a = NULL;
	php->size = php->capacity = 0;
}


返回栈顶元素
//HPDataType HeapTop(HP* php)
//{
//	assert(php);e
//	assert(!HeapEmpty(php));
//	return php->a[0];
//}

//判断是否为空
bool HeapEmpty(HP* php)
{
	assert(php);
	return php->size == 0;
}

//交换
void swap(HPDataType* a, HPDataType* b)
{
	HPDataType temp = *a;
	*a = *b;
	*b = temp;
}


//向上调整
void AdjustUp(HPDataType* a,int child)
{
	//父亲结点
	int parent = (child - 1) / 2;
	//终止条件：孩子等于0，大于0就继续调整
	//不要拿父亲作为条件,父亲和孩子都等于0的时候，paretn = (0-1)/2还是0，死循环了
	//while(parent>=0)
	while (child > 0)
	{
		//孩子小于父亲——小堆
		//如果要建大堆的话直接反过来就行了
		if (a[child] < a[parent])
		{
			swap(&a[child], &a[parent]);
			child = parent;
			parent = (child - 1) / 2;
		}
		else
		{
			break;
		}
	}
}

//插入x继续保持堆的形态
void HeapPush(HP* php, HPDataType x)
{
	assert(php);
	if (php->size == php->capacity)
	{
		int newCapacity = php->size == 0 ? 4 : php->capacity * 2;
		HPDataType* tmp = (HPDataType*)realloc(php->a, sizeof(HPDataType) * newCapacity);

		if (tmp == NULL)
		{
			perror("error");
			exit(-1);
		}
		php->a = tmp;
		php->capacity = newCapacity;
	}
	php->a[php->size]=x;
	php->size++;
	//向上调整，最后一个位置
	AdjustUp(php->a, php->size - 1);
}

void HeapPrint(HP* php)
{
	assert(php);
	assert(!HeapEmpty(php));
	for (int i = 0; i < php->size; i++)
	{
		printf("%d ", php->a[i]);
	}
	printf("\n");
		
}


//元素个数
int HeapSize(HP* php)
{
	assert(php);
	return php->size;
}

//返回堆顶元素
HPDataType HeapTop(HP* php)
{
	assert(php);
	assert(!HeapEmpty(php));
	return php->a[0];
}
//向下调整
AdjustDown(HPDataType* a,int size,int parent)
{
	//最小的默认为左孩子
	int minchild = 2 * parent + 1;
	while (minchild < size)
	{
		//找出小的孩子
		if (minchild + 1 < size && a[minchild + 1] < a[minchild])
		{
			minchild++;
		}
		if (a[minchild] < a[parent])
		{
			swap(&a[minchild], &a[parent]);
			parent = minchild;
			minchild = 2 * parent + 1;
		}
		else
		{
			break;
		}
		
	}
}
//删除堆顶元素——找出次大或者次小
void HeapPop(HP* php)
{
	assert(php);
	assert(!HeapEmpty(php));
	swap(&php->a[0], &php->a[php->size - 1]);
	php->size--;
	AdjustDown(php->a, php->size, 0);
}

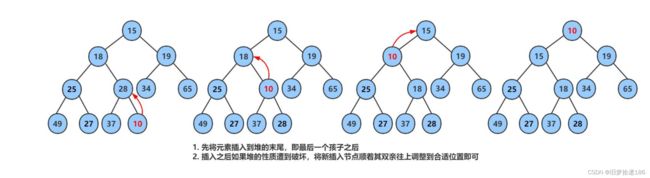
插入X并保持堆

插入之前是小根堆（假设堆已经创建好，后面会说到堆的创建，不要急，先看这一部分，便于理解，后面堆的创建就简单多了），我们是在尾部把X插入的，然后再进行向上调整（原来必须是大堆或者小堆了）。

比如先插入一个10到数组的尾上 ，再进行向上调整算法，直到满足堆 ：

//交换
void swap(HPDataType* a, HPDataType* b)
{
	HPDataType temp = *a;
	*a = *b;
	*b = temp;
}


//向上调整
void AdjustUp(HPDataType* a,int child)
{
	//父亲结点
	int parent = (child - 1) / 2;
	//终止条件：孩子等于0，大于0就继续调整
	//不要拿父亲作为条件,父亲和孩子都等于0的时候，paretn = (0-1)/2还是0，死循环了
	//while(parent>=0)
	while (child > 0)
	{
		//孩子小于父亲——小堆
		//如果要建大堆的话直接反过来就行了
		if (a[child] < a[parent])
		{
			swap(&a[child], &a[parent]);
			child = parent;
			parent = (child - 1) / 2;
		}
		else
		{
			break;
		}
	}
}

//插入x继续保持堆的形态
void HeapPush(HP* php, HPDataType x)
{
	assert(php);
	if (php->size == php->capacity)
	{
		int newCapacity = php->size == 0 ? 4 : php->capacity * 2;
		HPDataType* tmp = (HPDataType*)realloc(php->a, sizeof(HPDataType) * newCapacity);

		if (tmp == NULL)
		{
			perror("error");
			exit(-1);
		}
		php->a = tmp;
		php->capacity = newCapacity;
	}
	php->a[php->size]=x;
	php->size++;
	//向上调整，最后一个位置
	AdjustUp(php->a, php->size - 1);
}

开始之前，想想删除堆顶元素能干什么可以找出次大获知次小

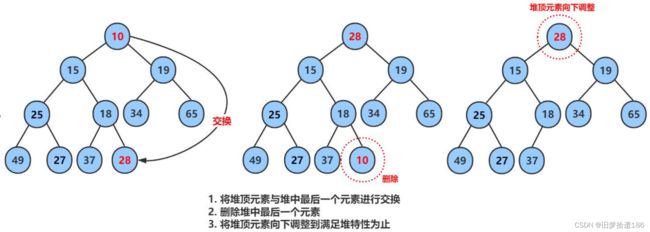
堆顶删除

删除堆是删除堆顶的数据，将堆顶的数据根最后一个数据一换，然后删除数组最后一个数据，再进行向下调整算法。

 

//向下调整
AdjustDown(HPDataType* a,int size,int parent)
{
	//最小的默认为左孩子
	int minchild = 2 * parent + 1;
	while (minchild < size)
	{
		//找出小的孩子
		if (minchild + 1 < size && a[minchild + 1] < a[minchild])
		{
			minchild++;
		}
		if (a[minchild] < a[parent])
		{
			swap(&a[minchild], &a[parent]);
			parent = minchild;
			minchild = 2 * parent + 1;
		}
		else
		{
			break;
		}
		
	}
}
//删除堆顶元素——找出次大或者次小
void HeapPop(HP* php)
{
	assert(php);
	assert(!HeapEmpty(php));
	swap(&php->a[0], &php->a[php->size - 1]);
	php->size--;
	AdjustDown(php->a, php->size, 0);
}