如何平衡机器学习中偏差与方差
本文介绍偏差与方差的概念和K折交叉验证，并通过示例展示其实现过程。
方差与偏差
为了评估模型在数据集上的表现，我们需要衡量模型预测与观测数据的匹配程度。对于回归模型，通常使用的指标是MSE(mean squared error)，其计算公式为：
MSE = (1/n)*Σ(y i {_i} i – f(x i {_i} i)) 2 {^2} 2
- n 为观测数据量
- y i {_i} i 第i个观测数据的响应值
- f(x i {_i} i)) 为第i个观测数据对于的预测值
模型预测值越接近响应值，则MSE越小。我们注意到MSE是通过看不见数据（测试数据集）计算的，但更应该关心的是如何面对不存在的数据（实际应用中的数据）。举例，如果模型基于历史数据预测股市走势非常好，但真正想要的是模型能够准确预测未来数据。
事实说明MSE总是可以分为两个部分：
- 方差
指的是使用不同训练集估计函数产生的变化量。
- 偏差
指用很简单模型逼近可能极其复杂的现实问题所产生的误差。
数学公式表示为：
Test MSE = Var(f(x 0 {_0} 0)) + [Bias(f(x 0 {_0} 0))] 2 {^2} 2 + Var(ε)
均方误差 = 方差 + 偏差 2 {^2} 2 + 未知误差
第三项表示未知错误，不能简单通过任何模型消除的误差，因为解释变量和响应变量关系中总是存在一些噪声。
模型有较高的偏差则对应方差趋向偏小。举例，简单线性关系模型有高偏差和低方差（模型评估从一个样本换为另一个样本不会变化太多）。
反之，模型有低偏差则方差趋于偏高。举例，复杂的非线性模型（没有假设响应变量与解释变量有明确关系）一般有低偏差和高方差（摸胸评估从一个样本换位另一个样本变化较大）。
偏差与方差平衡
偏差-方差权衡指的是当我们选择降低偏差(通常会增加方差)或降低方差(通常会增加偏差)时发生的权衡。
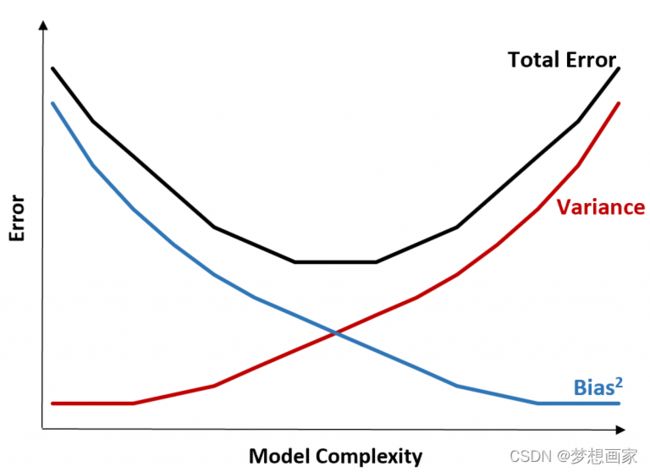
可以通过图形直观理解：
总误差随着模型复杂性的增加而减小，但仅到某一点。超过某一点，方差开始增加，总误差也开始增加。
在实践中，我们只关心最小化模型的总误差，而不一定要最小化方差或偏差。事实证明，最小化总误差的方法是在方差和偏差之间取得适当的平衡。换句话说，我们想要一个足够复杂的模型来捕捉解释变量和响应变量之间的真实关系，但又不能过于复杂，以至于它能发现实际上根本不存在的模式。
当一个模型过于复杂时，它会过度拟合数据。之所以会出现这种情况，是因为它很难在训练数据中找到只是由随机因素引起的模式。这种类型的模型在处理不可见数据时可能表现不佳。但是，当一个模型过于简单时，它就会与数据不符。这是因为它假设解释变量和响应变量之间的关系比实际更简单。
在机器学习中，选择最优模型的方法是在偏差和方差之间取得平衡，从而使模型对未来不可见数据的测试误差最小化。在实践中，最小化测试MSE的常见方法是使用交叉验证。
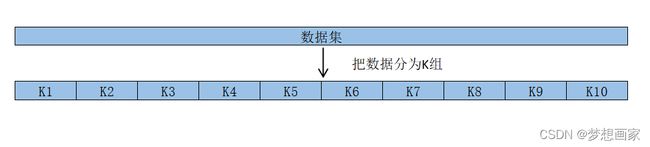
K折交叉验证
首先我们看下MSE的计算过程：
-
把数据集分为训练集和测试集
-
使用训练集构建模型
-
使用测试机进行预测并计算MSE
测试MSE让我们了解模型在处理之前从未见过的数据时的表现。然而只使用单个测试集的缺点是很大程度上过于依赖训练和测试过程中使用了哪些观察数据。
避免这个问题的常用方法是多次使用不同的训练和测试集拟合模型，然后计算所有测试MSE的平均值作为测试MSE。这种通用的方法被称为交叉验证，常用的交叉验证方法是K折交叉验证。
K折交叉验证过程如下：
-
随机把数据集分为K组，每组数据大致相等
-
选择其中一组作为测试集，使用其他剩下组作为训练集拟合模型，基于测试集计算MSE
-
重复这个过程K次，每次使用不同组作为测试集
-
计算所有测试MSE的平均值作为整个测试MSE
MSE = (1/k)* ∑ {\sum} ∑MSE i {_i} i
如何确定K值。一般来说，我们在k折交叉验证中使用的组数越多，检验MSE的偏差越低，但方差越高。相反使用的组数越少，偏差越高但方差越低。这是机器学习中偏方差权衡的经典问题。
在实践中通常选择使用5~10之间数值。正如在《统计学习导论》中所指出的，这已被证明在偏差和方差之间提供了最佳平衡。
通过使用k折交叉验证，我们通过训练集和测试集的几种不同变化来计算测试MSE，从而更有可能得到测试MSE的无偏估计。
R实现K折交叉验证
实现K折交叉验证，比较简单方式是使用caret包中的 trainControl() 函数。下面是示例数据集。
# 示例数据集
df <- data.frame(y=c(6, 8, 12, 14, 14, 15, 17, 22, 24, 23),
x1=c(2, 5, 4, 3, 4, 6, 7, 5, 8, 9),
x2=c(14, 12, 12, 13, 7, 8, 7, 4, 6, 5))
# 查看数据集
# df
下面代码利用上面数据集执行多重线性回归模型，并设定k=5，执行K折交叉验证评估模型表现。
library(caret)
# 指定交叉验证，设定k为5
ctrl <- trainControl(method = "cv", number = 5)
# 拟合回归模型，并使用k折交叉验证评估模型表现
model <- train(y ~ x1 + x2, data = df, method = "lm", trControl = ctrl)
# 查看模型概要信息
print(model)
# Linear Regression
#
# 10 samples
# 2 predictor
#
# No pre-processing
# Resampling: Cross-Validated (5 fold)
# Summary of sample sizes: 8, 8, 8, 8, 8
# Resampling results:
#
# RMSE Rsquared MAE
# 3.873277 1 3.589545
#
# Tuning parameter 'intercept' was held constant at a value of TRUE
我们对输出结果稍作解释：
-
没有进行预处理。也就是说在拟合模型之前，没有以任何方式对数据进行缩放(scale)
-
评估模型采用重采样方式是5折交叉验证
-
每次训练集的大小为8
-
RMSE: 均方根误差,它衡量的是模型预测与实际观测之间的平均差异。RMSE越低模型就越能准确地预测实际观测值。RMSE = Σ ( y i – y ^ i ) 2 / n \sqrt{Σ(y{_i} – ŷ{_i})^2 / n} Σ(yi–y^i)2/n
-
r²: 这是对模型预测和实际观测之间相关性的度量。r²越高，模型就越能准确预测实际观测值。
-
MAE: 平均绝对误差,这是模型预测和实际观测之间的平均绝对差。MAE越低，模型就越能准确预测实际观测结果。MAE = 1/n * Σ|y i {_i} i – ŷ i {_i} i|
输出的三个指标(RMSE、r²和MAE)都让我们了解模型在测试数据(看不见)上的表现。在实践中，我们通常拟合几个不同的模型，并比较上面三个度量指标，选择产生最低的测试误差的模型作为最佳。
下面的代码来检查最终的模型匹配:
# 查看最终模型
model$finalModel
# Call:
# lm(formula = .outcome ~ ., data = dat)
#
# Coefficients:
# (Intercept) x1 x2
# 21.2672 0.7803 -1.1253
通过输出得到最终模型为：
y = 21.2672 + 0.7803*(x1) – 1.12538(x2)
我们还可以查看每组测试的预测误差指标情况：
model$resample
# RMSE Rsquared MAE Resample
# 1 5.965809 1 5.556588 Fold1
# 2 4.267831 1 4.090775 Fold2
# 3 3.573658 1 3.457940 Fold3
# 4 3.119044 1 2.831199 Fold4
# 5 2.440045 1 2.011223 Fold5
这里我们选择了k=5，但可以选择任何组数。在实践中通常认为选择5到10次可产生可靠测试误差。