Python数据分析案例05——影响经济增长的因素(随机森林回归)

在计量经济学里面的研究，围绕着影响GDP的因素的研究有很多，基本都是做回归，拿GDP作为被解释变量y，其他因素作为解释变量x。然后做线性回归，时间序列就做自回归，面板数据就做固定效应等等。本次案例采用机器学习里面的随机森林回归来研究影响经济增长的因素，使用Python编程。选取人口，固定资产投资，消费，净出口，税收，广义M2货币，物价指数CPI作为解释变量X。我国GDP作为被解释变量y。

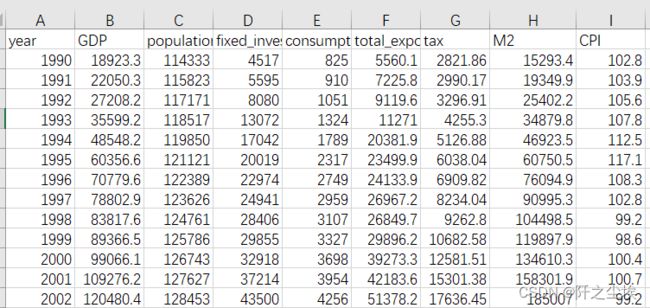
数据长这个样子，从1990年到2020年

 

---

首先导入包

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt 
import seaborn as sns
from sklearn.preprocessing import StandardScaler
import statsmodels.formula.api as smf
plt.rcParams ['font.sans-serif'] ='SimHei'              
plt.rcParams ['axes.unicode_minus']=False               
sns.set_style("darkgrid",{"font.sans-serif":[ 'Arial']})
#plt.rcParams['font.sans-serif'] = ['KaiTi']

读取数据，查看数据信息

spss = pd.read_excel('data.xlsx')
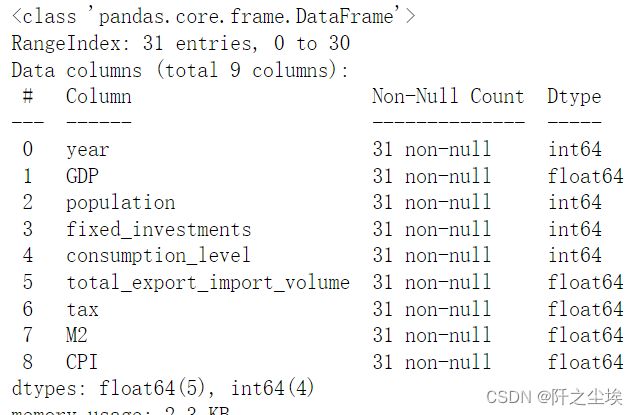
spss.info()
data=spss.copy()

 将时间设为索引

spss.set_index('year',inplace=True)
data.drop('year',axis=1,inplace=True)

---

 描述性统计

data.describe()  

计算每个变量的均值方差，分位数等

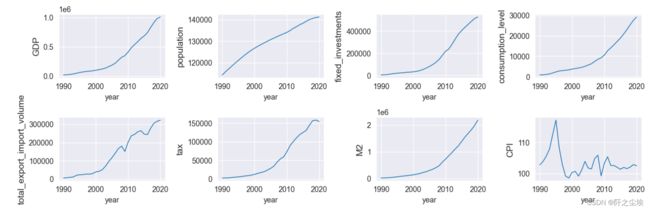
画出每个变量的随时间变化的折线图

#Sequence diagram of eight variables
column = data.columns.tolist() 
fig = plt.figure(figsize=(12,4), dpi=128) 
for i in range(8):
    plt.subplot(2,4, i + 1)  
    sns.lineplot(data=spss[column[i]],lw=1)  
    plt.ylabel(column[i], fontsize=12)
plt.tight_layout()
plt.show()

 所有变量都是单调增加，具有一致性趋势。

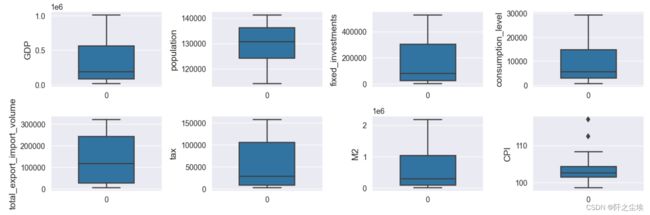
画所有变量的箱线图

#boxplot
column = data.columns.tolist() 
fig = plt.figure(figsize=(12,4), dpi=128)  
for i in range(8):
    plt.subplot(2,4, i + 1)  
    sns.boxplot(data=data[column[i]], orient="v",width=0.5)  
    plt.ylabel(column[i], fontsize=12)
plt.tight_layout()
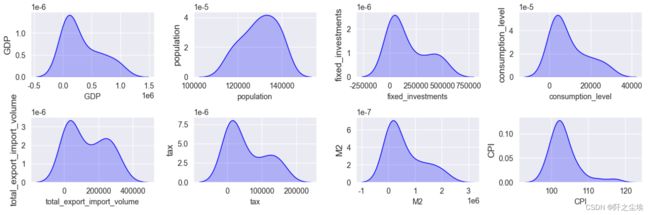
plt.show()

画核密度图

#kdeplot
column = data.columns.tolist() 
fig = plt.figure(figsize=(12,4), dpi=128)  
for i in range(8):
    plt.subplot(2,4, i + 1)  
    sns.kdeplot(data=data[column[i]],color='blue',shade= True) 
    plt.ylabel(column[i], fontsize=12)
plt.tight_layout()
plt.show()

 

 从箱线图和核密度图可以看出数据的分布都还比较集中，没有很多异常点。

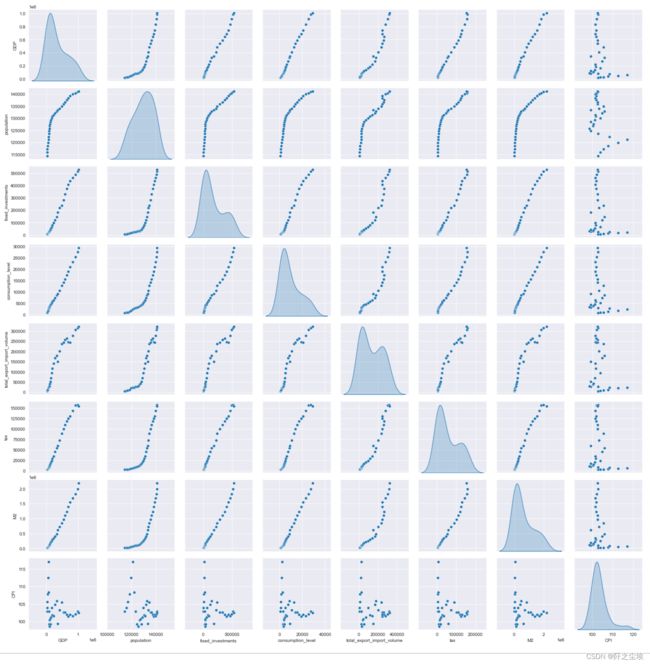
下面画所有变量两两之间的散点图

sns.pairplot(data[column],diag_kind='kde')
plt.savefig('Scatter plot.jpg',dpi=256)

 可以看到除了cpi，几乎所有变量之间都有线性关系，人口有点像二次抛物线。

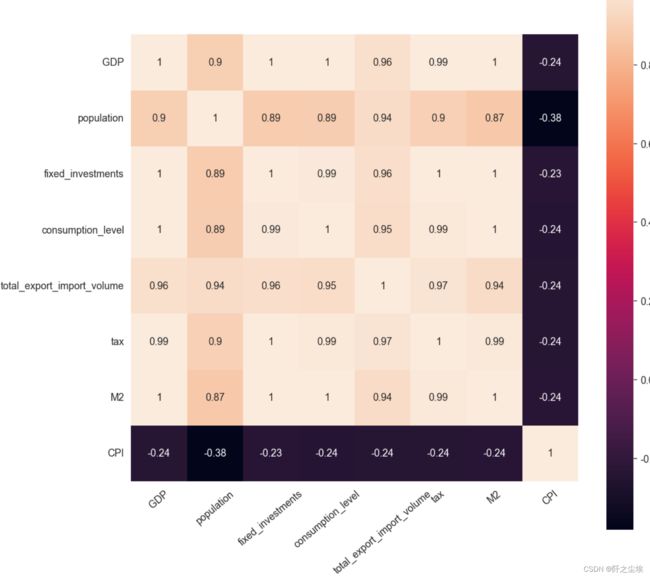
画皮尔逊相关系数热力图

#Pearson's correlation coefficient heatmap
corr = plt.figure(figsize = (10,10),dpi=128)
corr= sns.heatmap(data[column].corr(),annot=True,square=True)
plt.xticks(rotation=40)

 很多X之间都存在的高的相关性，经典的最小二乘线性模型可能存在着严重的多重共线性。

---

线性回归

还是做一下线性回归

import statsmodels.formula.api as smf
all_columns = "+".join(data.columns[1:])
print('x is ：'+all_columns)
formula = 'GDP~' + all_columns
print('The regression equation is ：'+formula)

写出回归方程后，带入ols模型

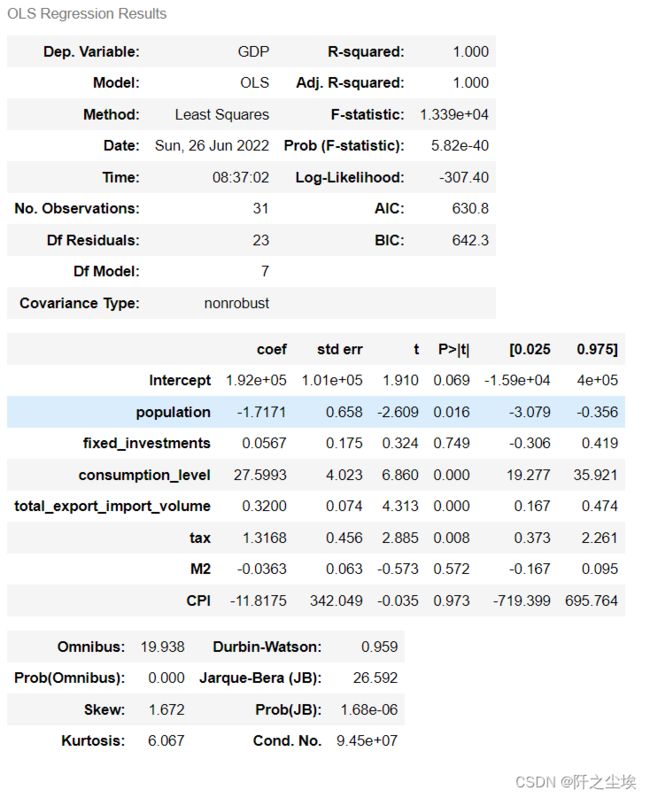
results = smf.ols(formula, data=data).fit()
results.summary()

 

 可以看到整体的拟合优度为100。。在0.05的显著性水平下，人口和消费，还有净出口税收都对GDP的变动具有显著性的影响。

有些变量不显着，可能是多重共线性的原因……下面的非参数回归方法——随机森林，可以避免多重共线性的影响，还能得到变量的重要特征排序

 

---

随机森林回归

取出X和y

X=data.iloc[:,1:]
y=data.iloc[:,0]

数据标准化

# data normalization
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaler.fit(X)
X_s= scaler.transform(X)
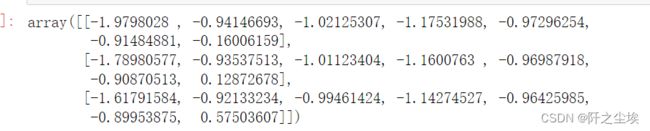
X_s[:3]

 随机森林模型拟合和评价

from sklearn.ensemble import RandomForestRegressor
model = RandomForestRegressor(n_estimators=5000, max_features=int(X.shape[1] / 3), random_state=0)
model.fit(X_s,y)
model.score(X_s,y)

 拟合优度也很高，99.96%

下面对比拟合值和真实值

pred = model.predict(X_s)
plt.scatter(pred, y, alpha=0.6)
w = np.linspace(min(pred), max(pred), 100)
plt.plot(w, w)
plt.xlabel('pred')
plt.ylabel('y_test')
plt.title('Comparison of GDP fitted value and true value')

 可以看到两者基本都在一条线上，说明效果很好

计算每个变量的重要性

print(model.feature_importances_)
sorted_index = model.feature_importances_.argsort()

画图可视化

plt.barh(range(X.shape[1]), model.feature_importances_[sorted_index])
plt.yticks(np.arange(X.shape[1]),X.columns[sorted_index],fontsize=14)
plt.xlabel('X Importance',fontsize=12)
plt.ylabel('covariate X',fontsize=12)
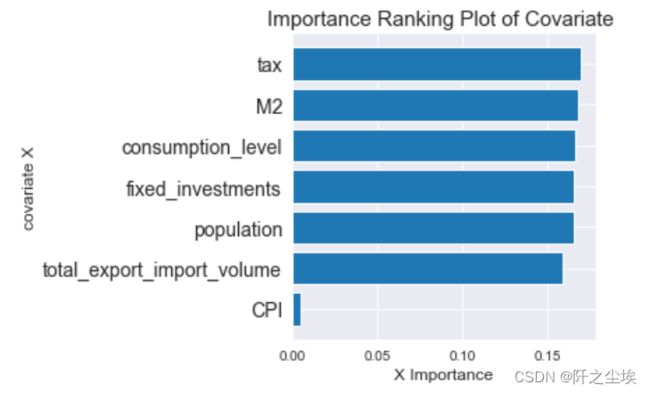
plt.title('Importance Ranking Plot of Covariate ',fontsize=15)
plt.tight_layout()

 

 结论，影响GDP的变量重要性排序：
税收>M2>消费>投资>人口>出口进口量>CPI

当然实际科研中也可以选择更多的变量，随机森林不怕多重共线性，是要变量越多越好。