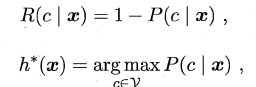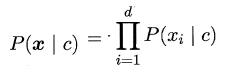【进阶版】机器学习之贝叶斯分类器细节回顾及原理完善（10）

欢迎订阅本专栏，持续更新中~

本专栏包含大量代码项目，适用于毕业设计方向选取和实现、科研项目代码指导，每一篇文章都是通过原理讲解+代码实战进行思路构建的，如果有需要这方面的指导可以私信博主，获取相关资源及指导！

本专栏前期文章介绍！

机器学习算法知识、数据预处理、特征工程、模型评估——原理+案例+代码实战

机器学习之Python开源教程——专栏介绍及理论知识概述
机器学习框架及评估指标详解
Python监督学习之分类算法的概述
数据预处理之数据清理，数据集成，数据规约，数据变化和离散化
特征工程之One-Hot编码、label-encoding、自定义编码
卡方分箱、KS分箱、最优IV分箱、树结构分箱、自定义分箱
特征选取之单变量统计、基于模型选择、迭代选择

机器学习八大经典分类万能算法——代码+案例项目开源、可直接应用于毕设+科研项目

机器学习分类算法之朴素贝叶斯
【万字详解·附代码】机器学习分类算法之K近邻（KNN）
《全网最强》详解机器学习分类算法之决策树（附可视化和代码）
机器学习分类算法之支持向量机
机器学习分类算法之Logistic 回归（逻辑回归）
机器学习分类算法之随机森林（集成学习算法）
机器学习分类算法之XGBoost（集成学习算法）
机器学习分类算法之LightGBM（梯度提升框架）

机器学习自然语言、推荐算法等领域知识——代码案例开源、可直接应用于毕设+科研项目

【原理+代码】Python实现Topsis分析法（优劣解距离法）
机器学习推荐算法之关联规则（Apriori）——支持度；置信度；提升度
机器学习推荐算法之关联规则Apriori与FP-Growth算法详解
机器学习推荐算法之协同过滤（基于用户）【案例+代码】
机器学习推荐算法之协同过滤（基于物品）【案例+代码】
预测模型构建利器——基于logistic的列线图（R语言）
基于surprise模块快速搭建旅游产品推荐系统（代码+原理）
机器学习自然语言处理之英文NLTK（代码+原理）
机器学习之自然语言处理——中文分词jieba库详解（代码+原理）
机器学习之自然语言处理——基于TfidfVectorizer和CountVectorizer及word2vec构建词向量矩阵（代码+原理）

机器学习配套资源推送

专栏配套资源推荐——部分展示（有需要可去对应文章或者评论区查看，可做毕设、科研参考资料）

自然语言处理之文本分类及文本情感分析资源大全（含代码及其数据，可用于毕设参考！）
基于Word2Vec构建多种主题分类模型（贝叶斯、KNN、随机森林、决策树、支持向量机、SGD、逻辑回归、XGBoost…）
基于Word2Vec向量化的新闻分本分类.ipynb
智能词云算法（一键化展示不同类型的词云图）运行生成HTML文件
协同过滤推荐系统资源（基于用户-物品-Surprise）等案例操作代码及讲解
Python机器学习关联规则资源（apriori算法、fpgrowth算法）原理讲解
机器学习-推荐系统（基于用户）.ipynb
机器学习-推荐系统（基于物品）.ipynb
旅游消费数据集——包含用户id，用户评分、产品类别、产品名称等指标，可以作为推荐系统的数据集案例

进阶版机器学习文章更新~

【进阶版】机器学习之基本术语及模评估与选择概念总结（01）
【进阶版】机器学习之模型性能度量及比较检验和偏差与方差总结（02）
【进阶版】机器学习之特征工程介绍及优化方法引入（03）
【进阶版】机器学习之特征降维、超参数调优及检验方法（04）
【进阶版】机器学习之线性模型介绍及过拟合欠拟合解决方法岭回归、loss回归、elasticnet回归（05）
【进阶版】机器学习之决策树知识与易错点总结（06）
【进阶版】机器学习之神经网络与深度学习基本知识和理论原理（07）
【进阶版】机器学习与深度学习之前向传播与反向传播知识（08）
【进阶版】机器学习之支持向量机细节回顾及原理完善（09）

---

前期我们对机器学习的基础知识，从基础的概念到实用的代码实战演练，并且系统的了解了机器学习在分类算法上面的应用，同时也对机器学习的准备知识有了一个相当大的了解度，而且还拓展了一系列知识，如推荐算法、文本处理、图像处理。以及交叉学科的应用，那么前期你如果认真的了解了这些知识，并加以利用和实现，相信你已经对机器学习有了一个“量”的认识，接下来的，我将带你继续学习机器学习学习，并且全方位，系统性的了解和深入机器学习领域，达到一个“质”的变化。

---

点击下方下载高清版学习知识图册

机器学习Python算法知识点大全，包含sklearn中的机器学习模型和Python预处理的pandas和numpy知识点

---

本篇将讨论一个经典的统计学习算法–贝叶斯分类器。

贝叶斯分类器

贝叶斯分类器是一种概率框架下的统计学习分类器，对分类任务而言，假设在相关概率都已知的情况下，贝叶斯分类器考虑如何基于这些概率为样本判定最优的类标。在开始介绍贝叶斯决策论之前，我们首先来回顾下概率论 --贝叶斯公式。

贝叶斯决策论

若将上述定义中样本空间的划分$B_i$看做为类标，A看做为一个新的样本，则很容易将条件概率理解为样本A是类别$B_i$的概率。在机器学习训练模型的过程中，往往我们都试图去优化一个风险函数，因此在概率框架下我们也可以为贝叶斯定义“条件风险”（conditional risk）。

我们的任务就是寻找一个判定准则最小化所有样本的条件风险总和，因此就有了贝叶斯判定准则（Bayes decision rule）:为最小化总体风险，只需在每个样本上选择那个使得条件风险最小的类标。

若损失函数λ取0-1损失，则有：

即对于每个样本x，选择其后验概率$P（c|x）$最大所对应的类标，能使得总体风险函数最小，从而将原问题转化为估计后验概率$P（c|x）$。一般这里有两种策略来对后验概率进行估计：

• 判别式模型：直接对 P（c | x）进行建模求解。前面所介绍的决策树、神经网络、SVM都是属于判别式模型。
• 生成式模型：通过先对联合分布P（x,c）建模，从而进一步求解 P（c | x）。

贝叶斯分类器就属于生成式模型，基于贝叶斯公式对后验概率P（c | x） 进行一项神奇的变换… P（c | x）变身：

对于给定的样本x，P（x）与类标无关，P（c）称为类先验概率，p（x | c ）称为类条件概率。这时估计后验概率P（c | x）就变成为估计类先验概率和类条件概率的问题。对于先验概率和后验概率，在看这章之前也是模糊了我好久，这里普及一下它们的基本概念。

• 先验概率： 根据以往经验和分析得到的概率。
• 后验概率：后验概率是基于新的信息，修正原来的先验概率后所获得的更接近实际情况的概率估计。

实际上先验概率就是在没有任何结果出来的情况下估计的概率，而后验概率则是在有一定依据后的重新估计，直观意义上后验概率就是条件概率。

例如：

对于类先验概率P（c），p（c）就是样本空间中各类样本所占的比例，根据大数定理（当样本足够多时，频率趋于稳定等于其概率），这样当训练样本充足时，p（c） 可以使用各类出现的频率来代替。

因此只剩下类条件概率p（x | c ），它表达的意思是在类别c中出现x的概率，它涉及到属性的联合概率问题，若只有一个离散属性还好，当属性多时采用频率估计起来就十分困难，因此这里一般采用极大似然法进行估计。

极大似然法

极大似然估计（Maximum Likelihood Estimation，简称MLE），是一种根据数据采样来估计概率分布的经典方法。常用的策略是先假定总体具有某种确定的概率分布，再基于训练样本对概率分布的参数进行估计。

运用到类条件概率p（x | c ）中，假设p（x | c ）服从一个参数为θ的分布，问题就变为根据已知的训练样本来估计θ。极大似然法的核心思想就是：估计出的参数使得已知样本出现的概率最大，即使得训练数据的似然最大。

所以，贝叶斯分类器的训练过程就是参数估计。总结最大似然法估计参数的过程，一般分为以下四个步骤：

• 1.写出似然函数；
• 2.对似然函数取对数，并整理；
• 3.求导数，令偏导数为0，得到似然方程组；
• 4.解似然方程组，得到所有参数即为所求。

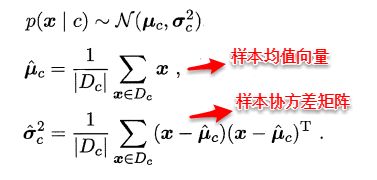
例如：假设样本属性都是连续值，p（x | c ）服从一个多维高斯分布，则通过MLE计算出的参数刚好分别为：

上述结果看起来十分合乎实际，但是采用最大似然法估计参数的效果很大程度上依赖于作出的假设是否合理，是否符合潜在的真实数据分布。这就需要大量的经验知识，搞统计越来越值钱也是这个道理，大牛们掐指一算比我们搬砖几天更有效果。

朴素贝叶斯分类器

=原始的贝叶斯分类器最大的问题在于联合概率密度函数的估计，首先需要根据经验来假设联合概率分布，其次当属性很多时，训练样本往往覆盖不够，参数的估计会出现很大的偏差。

为了避免这个问题，朴素贝叶斯分类器（naive Bayes classifier）采用了“属性条件独立性假设” ，即样本数据的所有属性之间相互独立。这样类条件概率p（x | c ）可以改写为：

这样，为每个样本估计类条件概率变成为每个样本的每个属性估计类条件概率。

相比原始贝叶斯分类器，朴素贝叶斯分类器基于单个的属性计算类条件概率更加容易操作，需要注意的是：若某个属性值在训练集中和某个类别没有一起出现过，这样会抹掉其它的属性信息，因为该样本的类条件概率被计算为0。因此在估计概率值时，常常用进行平滑（smoothing）处理，拉普拉斯修正（Laplacian correction）就是其中的一种经典方法，具体计算方法如下：

当训练集越大时，拉普拉斯修正引入的影响越来越小。对于贝叶斯分类器，模型的训练就是参数估计，因此可以事先将所有的概率储存好，当有新样本需要判定时，直接查表计算即可。

针对朴素贝叶斯，人们觉得它too sample，sometimes too naive！因此又提出了半朴素的贝叶斯分类器，具体有SPODE、TAN、贝叶斯网络等来刻画属性之间的依赖关系，此处不进行深入。

代码实现

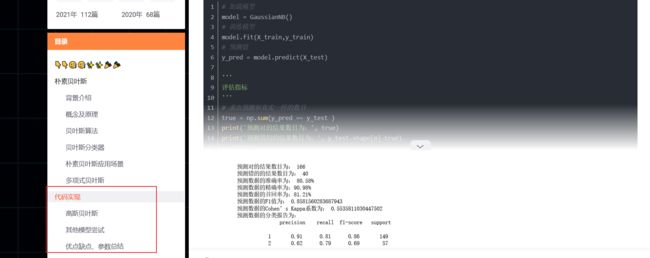
参考这篇文章，这是在最初的机器学习——分类算法上，通过案例+代码进行完整复现

机器学习分类算法之朴素贝叶斯

每文一语

快乐,其实很简单,只要我们有一颗能感受快乐的心。