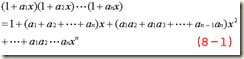HDOJ2082结题报告——找单词
Problem Description
假设有x1个字母A, x2个字母B,..... x26个字母Z,同时假设字母A的价值为1,字母B的价值为2,..... 字母Z的价值为26。那么,对于给定的字母,可以找到多少价值<=50的单词呢?单词的价值就是组成一个单词的所有字母的价值之和,比如,单词 ACM的价值是1+3+14=18,单词HDU的价值是8+4+21=33。(组成的单词与排列顺序无关,比如ACM与CMA认为是同一个单词)。
Input
输入首先是一个整数N,代表测试实例的个数。
然后包括N行数据,每行包括26个<=20的整数x1,x2,.....x26.
Output
对于每个测试实例,请输出能找到的总价值<=50的单词数,每个实例的输出占一行。
Sample Input
2 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 9 2 6 2 10 2 2 5 6 1 0 2 7 0 2 2 7 5 10 6 10 2 10 6 1 9
Sample Output
7 379297
该题就是典型的母函数(Generation function)及其应用,在数学中,某个序列的母函数是一种形式幂级数,其每一项的系数可以提供关于这个序列的信息。使用母函数解决问题的方法称为母函数方法。母函数可分为很多种,包括普通母函数、指数母函数、L级数、贝尔级数和狄利克雷级数。对每个序列都可以写出以上每个类型的一个母函数。构造母函数的目的一般是为了解决某个特定的问题,因此选用何种母函数视乎序列本身的特性和问题的类型。所谓整数拆分即把整数分解成若干整数的和(相当于把n个无区别的球放到n个无标志的盒子,盒子允许空,也允许放多于一个球)。整数拆分成若干整数的和,办法不一,不同拆分法的总数叫做拆分数。
可以看出:
x2项的系数a1a2+a1a3+...+an-1an中所有的项包括n个元素a1,a2, …an中取两个组合的全体;
同理:x3项系数包含了从n个元素a1,a2, …an中取3个元素组合的全体;
以此类推。
若令a1=a2= …=an=1,在(8-1)式中a1a2+a1a3+...+an-1an项系数中每一个组合有1个贡献,其他各项以此类推。故有:![]()
称函数G(x)是序列a0,a1,a2,…的母函数,(1+x)n是序列C(n,0),C(n,1),...,C(n,n)的母函数。如若已知序列a0,a1,a2,…则对应的母函数G(x)便可根据定义给出。反之,如若已经求得序列的母函数G(x),则该序列也随之确定。序列a0,a1,a2,…可记为{an} 。
- 实例分析:
例1:若有1克、2克、3克、4克的砝码各一枚,能称出哪几种重量?各有几种可能方案?
如何解决这个问题呢?考虑构造母函数。
如果用x的指数表示称出的重量,则:
1个1克的砝码可以用函数1+x表示,
1个2克的砝码可以用函数1+x2表示,
1个3克的砝码可以用函数1+x3表示,
1个4克的砝码可以用函数1+x4表示。
几种砝码的组合可以称重的情况,可以用以上几个函数的乘积表示:
(1+x)(1+x2)(1+x3)(1+x4)
=(1+x+x2+x3)(1+x3+x4+x7)
=1+x+x2+2x3+2x4+2x5+2x6+2x7+x8+x9+x10
从上面的函数知道:可称出从1克到10克,系数便是方案数。
例如右端有2x5 项,即称出5克的方案有2:5=3+2=4+1;同样,6=1+2+3=4+2;10=1+2+3+4。
故称出6克的方案有2,称出10克的方案有1
例2:求用1分、2分、3分的邮票贴出不同数值的方案数——
因邮票允许重复,故母函数为: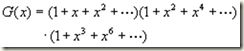
以展开后的x4为例,其系数为4,即4拆分成1、2、3之和的拆分数为4;
即 :4=1+1+1+1=1+1+2=1+3=2+2
- 概念:整数拆分
n所谓整数拆分即把整数分解成若干整数的和(相当于把n个无区别的球放到n个无标志的盒子,盒子允许空,也允许放多于一个球)。
n整数拆分成若干整数的和,办法不一,不同拆分法的总数叫做拆分数。
下面附上本体代码:
#include<iostream>
#include<iomanip>
#include<string>
#include<cmath>
using namespace std;
int main()
{
int n;
int i,j,k;
int data[27];
int c1[10000],c2[10000];
while(cin>>n&&n!=EOF){
for(i=0;i<n;i++)
{
int sum=0;
for(int j=1;j<=26;j++)
{
cin>>data[j];
}
for(int j=0;j<=50;j++)
{
c1[j]=0;
c2[j]=0;
}
for(int j=0;j<=data[1];j++)
c1[j]=1;
for(int j=2;j<=26;j++)
{
for(int k=0;k<=50;k++)
for(int p=0;p<=j*data[j];p+=j)
c2[k+p]=c2[k+p]+c1[k];
for(int k=0;k<=50;k++)
{
c1[k]=c2[k];
c2[k]=0;
}
}
for(int i=1;i<=50;i++)
sum+=c1[i];
cout<<sum<<endl;
}
}
}
由题意得知是要计算所有单词的组合,其质量和小于等于50的组合数,首先定义c1[],c2[]数组,c1[]用于保存多项式的系数,c2[]是中间量,保存每一次就是相邻两个多项式的系数的情况。开始对c1[]c2[]做初始化为0,for(int j=0;j<=data[1];j++) c1[j]=1; 这一步就是给第一个多项式的系数赋值(1+x+x^2+x^3…….),然后从第二个到26个多项式遍历即:第一个多项式*第二个多项式,记录其系数,然后将计算后结果与第三个多项式相乘,如此循环
for(int k=0;k<=50;k++)
for(int p=0;p<=j*data[j];p+=j)
c2[k+p]=c2[k+p]+c1[k];
这里k其实就是前面计算后的x的指数,指数就是单词的总重量,由于要计算小于等于50,所以只遍历0到50,就是单个多项式的x的指数,k+p就是相乘后的指数和,最后c2记录了该次乘积后结果的系数情况,for(int k=0;k<=50;k++) { c1[k]=c2[k]; c2[k]=0; } 这一步就是将结果让c1保存,c2重新赋值为0,继续下一次的循环。