数学建模:图论模型 — 最短路问题的 Python 求解
求固定起点到其余各点的最短路 (Dijkstra 算法)
例 1: 用 Dijkstra 算法求下图 v 1 v_1 v1 到其余各顶点的最短路及最短距离
import numpy as np
import networkx as nx
def Dijkstra_all_minpath(matr,start): #matr为邻接矩阵的数组,start表示起点
n=len( matr) #该图的节点数
dis=[]; temp=[]
dis.extend(matr[start]) #添加数组matr的start行元素
temp.extend(matr[start]) #添加矩阵matr的start行元素
temp[start] = np.inf #临时数组会把处理过的节点的值变成 \infty
visited=[start] #start已处理
parent=[start]*n #用于画路径,记录此路径中该节点的父节点
while len(visited)<n:
i= temp.index(min(temp)) #找最小权值的节点的坐标
temp[i]=np.inf
for j in range(n):
if j not in visited:
if (dis[i]+ matr[i][j])<dis[j]:
dis[j] = temp[j] =dis[i]+ matr[i][j]
parent[j]=i #说明父节点是i
visited.append(i) #该索引已经处理了
path=[] #用于画路径
path.append(str(i+1))
k=i
while(parent[k]!=start): #找该节点的父节点添加到path,直到父节点是start
path.append(str(parent[k]+1))
k=parent[k]
path.append(str(start+1))
path.reverse() #path反序产生路径
print(str(i+1)+':','->'.join(path)) #打印路径
return dis
a=[[0, 1, 4, np.inf, np.inf, np.inf],
[1, 0, 2, 7, 5, np.inf],
[4, 2, 0, np.inf, 1, np.inf],
[np.inf, 7, np.inf, 0, 3, 2],
[np.inf, 5, 1, 3, 0, 6],
[np.inf, np.inf, np.inf, 2, 6, 0]]
s=0
d=Dijkstra_all_minpath(a,s)
print(f"v{s+1}到所有顶点的最短距离为: {d}")
2: 1->2
3: 1->2->3
5: 1->2->3->5
4: 1->2->3->5->4
6: 1->2->3->5->4->6
v1到所有顶点的最短距离为: [0, 1, 3, 7, 4, 9]
例 2: 求邻接矩阵如下的图从 v 3 v_{3} v3 到所有其余顶点的最短路及最短距离
W = [ 0 1 2 ∞ 7 ∞ 4 8 1 0 2 3 ∞ ∞ ∞ 7 2 2 0 1 5 ∞ ∞ ∞ ∞ 3 1 0 3 6 ∞ ∞ 7 ∞ 5 3 0 4 3 ∞ ∞ ∞ ∞ 6 4 0 6 4 4 ∞ ∞ ∞ 3 6 0 2 8 7 ∞ ∞ ∞ 4 2 0 ] W=\left[\begin{array}{c} 0 & 1 & 2 & \infty & 7 & \infty & 4 & 8 \\ 1 & 0 & 2 & 3 & \infty & \infty & \infty & 7 \\ 2 & 2 & 0 & 1 & 5 & \infty & \infty & \infty \\ \infty & 3 & 1 & 0 & 3 & 6 & \infty & \infty \\ 7 & \infty & 5 & 3 & 0 & 4 & 3 & \infty \\ \infty & \infty & \infty & 6 & 4 & 0 & 6 & 4 \\ 4 & \infty & \infty & \infty & 3 & 6 & 0 & 2 \\ 8 & 7 & \infty & \infty & \infty & 4 & 2 & 0 \end{array}\right] W=⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡012∞7∞481023∞∞∞722015∞∞∞∞31036∞∞7∞53043∞∞∞∞640644∞∞∞360287∞∞∞420⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤
用 Dijkstra 算法求解
# Dijkstra 算法
import numpy as np
inf=np.inf
def Dijkstra_all_minpath(matr,start): #matr为邻接矩阵的数组,start表示起点
n=len( matr) #该图的节点数
dis=[]; temp=[]
dis.extend(matr[start]) #添加数组matr的start行元素
temp.extend(matr[start]) #添加矩阵matr的start行元素
temp[start] = np.inf #临时数组会把处理过的节点的值变成 \infty
visited=[start] #start已处理
parent=[start]*n #用于画路径,记录此路径中该节点的父节点
while len(visited)<n:
i= temp.index(min(temp)) #找最小权值的节点的坐标
temp[i]=np.inf
for j in range(n):
if j not in visited:
if (dis[i]+ matr[i][j])<dis[j]:
dis[j] = temp[j] =dis[i]+ matr[i][j]
parent[j]=i #说明父节点是i
visited.append(i) #该索引已经处理了
path=[] #用于画路径
path.append(str(i))
k=i
while(parent[k]!=start): #找该节点的父节点添加到path,直到父节点是start
path.append(str(parent[k]))
k=parent[k]
path.append(str(start))
path.reverse() #path反序产生路径
print(str(i)+':','->'.join(path)) #打印路径
return dis
a=[[0,1,2,np.inf,7,np.inf,4,8],[1,0,2,3,np.inf,np.inf,np.inf,7],
[2,2,0,1,5,np.inf,np.inf,np.inf],[np.inf,3,1,0,3,6,np.inf,np.inf],
[7,np.inf,5,3,0,4,3,np.inf],[np.inf,np.inf,np.inf,6,4,0,6,4],
[4,np.inf,np.inf,np.inf,3,6,0,2],[8,7,np.inf,np.inf,np.inf,4,2,0]]
d=Dijkstra_all_minpath(a,3)
print("v3到所有顶点的最短距离为:",d)
2: 3->2
0: 3->2->0
1: 3->1
4: 3->4
5: 3->5
6: 3->4->6
7: 3->4->6->7
v3到所有顶点的最短距离为: [3, 3, 1, 0, 3, 6, 6, 8]
用 Dijkstra 算法求固定起点到其他顶点的最短路还可以直接调用 networkx 的库函数 dijkstra_path(G, source, target, weight='weight') 求最短路径, dijkstra_path_length(G, source, target, weight='weight') 求最短距离, 其中 G 为 NetworkX 图, source 为起点, target 为终点.
需要注意在利用 networkx 库函数计算时, 如果两个顶点之间没有边, 对应的邻接矩阵元素为 0, 而不是像数学理论上对应的邻接矩阵元素为 + ∞ +\infty +∞. 下面同样约定算法上的数学邻接矩阵和 networkx 库函数调用时的邻接矩阵是不同的.
# networkx 库函数
import numpy as np
import networkx as nx
List=[(0,1,1),(0,2,2),(0,4,7),(0,6,4),(0,7,8),(1,2,2),(1,3,3),
(1,7,7),(2,3,1),(2,4,5),(3,4,3),(3,5,6),(4,5,4),(4,6,3),
(5,6,6),(5,7,4),(6,7,2)]
G=nx.Graph()
G.add_weighted_edges_from(List)
#A=nx.to_numpy_matrix(G, nodelist=range(8)) #导出邻接矩阵
p=nx.dijkstra_path(G, source=3, target=7, weight='weight') #求最短路径;
d=nx.dijkstra_path_length(G, 3, 7, weight='weight') #求最短距离
print("v3到v7最短路径为:",p,";最短距离为:",d)
v3到v7最短路径为: [3, 4, 6, 7] ;最短距离为: 8
求每对顶点间的最短路 (Floyd 算法)
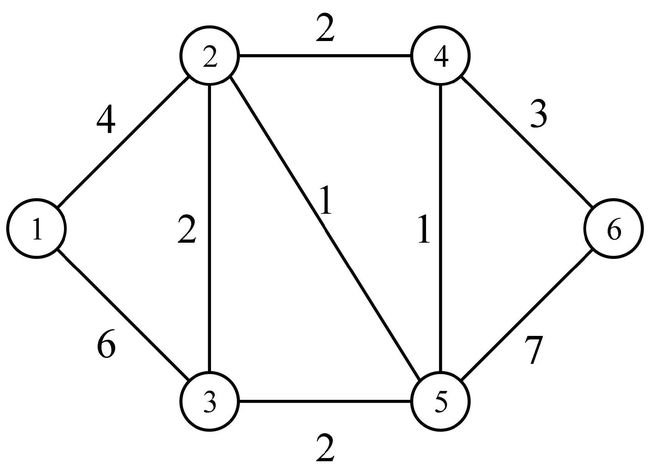
例 3: 求下图所有顶点对之间的最短距离矩阵与路由矩阵
import numpy as np
def floyd(graph):
m = len(graph)
dis = graph
path = np.zeros((m, m)) #路由矩阵初始化
for k in range(m):
for i in range(m):
for j in range(m):
if dis[i][k] + dis[k][j] < dis[i][j]:
dis[i][j] = dis[i][k] + dis[k][j]
path[i][j] = k
return dis, path
inf=np.inf
A=np.array([[0, 4, 6, inf,inf,inf],
[4, 0, 2, 2, 1, inf],
[6, 2, 0, inf,2, inf],
[inf,2, inf,2, 1, 3 ],
[inf,1, 2, 1, 0, 7 ],
[inf,inf,inf,3, 7, 0 ]]) #输入邻接矩阵
dis, path=floyd(A)
print(f"所有顶点对之间的最短距离为: \n{dis}\n路由矩阵为: \n{path}")
所有顶点对之间的最短距离为:
[[0. 4. 6. 6. 5. 9.]
[4. 0. 2. 2. 1. 5.]
[6. 2. 0. 3. 2. 6.]
[6. 2. 3. 2. 1. 3.]
[5. 1. 2. 1. 0. 4.]
[9. 5. 6. 3. 4. 0.]]
路由矩阵为:
[[0. 0. 0. 1. 1. 3.]
[0. 0. 0. 0. 0. 3.]
[0. 0. 0. 4. 0. 4.]
[1. 0. 4. 0. 0. 0.]
[1. 0. 0. 0. 0. 3.]
[3. 3. 4. 0. 3. 0.]]
例 4: 续例 2, 求所有顶点对之间的最短距离矩阵与路由矩阵
import numpy as np
def floyd(graph):
m = len(graph)
dis = graph
path = np.zeros((m, m)) #路由矩阵初始化
for k in range(m):
for i in range(m):
for j in range(m):
if dis[i][k] + dis[k][j] < dis[i][j]:
dis[i][j] = dis[i][k] + dis[k][j]
path[i][j] = k
return dis, path
inf=np.inf
a=np.array([[0 , 1 , 2 , inf,7 , inf,4 , 8 ],
[1 , 0 , 2 , 3 , inf,inf,inf,7 ],
[2 , 2 , 0 , 1 , 5 , inf,inf,inf],
[inf,3 , 1 , 0 , 3 , 6 , inf,inf],
[7 , inf,5 , 3 , 0 , 4 , 3 , inf],
[inf,inf,inf,6 , 4 , 0 , 6 , 4 ],
[4 , inf,inf,inf,3 , 6 , 0 , 2 ],
[8 , 7 , inf,inf,inf,4 , 2 , 0 ]]) #输入邻接矩阵
dis, path=floyd(a)
print(f"所有顶点对之间的最短距离为: \n{dis}\n路由矩阵为: \n{path}")
所有顶点对之间的最短距离为:
[[0. 1. 2. 3. 6. 9. 4. 6.]
[1. 0. 2. 3. 6. 9. 5. 7.]
[2. 2. 0. 1. 4. 7. 6. 8.]
[3. 3. 1. 0. 3. 6. 6. 8.]
[6. 6. 4. 3. 0. 4. 3. 5.]
[9. 9. 7. 6. 4. 0. 6. 4.]
[4. 5. 6. 6. 3. 6. 0. 2.]
[6. 7. 8. 8. 5. 4. 2. 0.]]
路由矩阵为:
[[0. 0. 0. 2. 3. 3. 0. 6.]
[0. 0. 0. 0. 3. 3. 0. 0.]
[0. 0. 0. 0. 3. 3. 0. 6.]
[2. 0. 0. 0. 0. 0. 4. 6.]
[3. 3. 3. 0. 0. 0. 0. 6.]
[3. 3. 3. 0. 0. 0. 0. 0.]
[0. 0. 0. 4. 0. 0. 0. 0.]
[6. 0. 6. 6. 6. 0. 0. 0.]]
求每对顶点间的最短路也可用 networkx 的库函数, networkx 求所有顶点对之间最短路径的函数为
shortest_path(G, source=None, target=None, weight=None, method='dijkstra')
其中 source 是起点, target 是终点, 如果未指定, 则计算所有可能节点的最短路径; method 是用于计算路径的算法, 可以取值 'dijkstra', 'bellman-ford'.
返回值是可迭代对象: 路径的列表或字典: 如果同时指定了起点和终点, 则返回从起点到终点的最短路径中的节点的列表;
如果仅指定了起点, 则返回一个键为终点, 值为从起点到这个终点的最短路径的节点的列表的字典;
如果仅指定了终点, 则返回一个键为起点, 值为从这个起点到终点的最短路径的节点的列表的字典;
如果既没有指定起点也没有指定终点, 则返回 path[source][target]=[list of nodes in path] 的字典.
networkx 求所有顶点对之间最短距离的函数为
shortest_path_length(G, source=None, target=None, weight=None, method='dijkstra')
参数与 shortest_path 相同.
返回值是长度: 整数或可迭代对象: 如果同时指定了起点和终点, 则返回从起点到终点的最短路径的长度;
如果只指定了起点, 则返回一个键为终点, 值为从起点到该终点的最短路径长度的字典;
如果只指定了终点,则返回一个键为起点,值为从该起点到终点的最短路径长度的字典;
如果既没有指定起点也没有指定终点, 则返回一个迭代器 (source, dictionary), 其中字典 dictionary 键为终点, 值为从起点到该终点的最短路径长度.
import numpy as np
import networkx as nx
a=np.array([[0 , 1 , 2 , 0 , 7 , 0 , 4 , 8 ],
[1 , 0 , 2 , 3 , 0 , 0 , 0 , 7 ],
[2 , 2 , 0 , 1 , 5 , 0 , 0 , 0 ],
[0 , 3 , 1 , 0 , 3 , 6 , 0 , 0 ],
[7 , 0 , 5 , 3 , 0 , 4 , 3 , 0 ],
[0 , 0 , 0 , 6 , 4 , 0 , 6 , 4 ],
[4 , 0 , 0 , 0 , 3 , 6 , 0 , 2 ],
[8 , 7 , 0 , 0 , 0 , 4 , 2 , 0 ]]) #输入邻接矩阵
G=nx.Graph(a) #利用邻接矩阵构造赋权无向图
d=nx.shortest_path_length(G,weight='weight') #返回值是可迭代类型
Ld=dict(d) #转换为字典类型
print("顶点对之间的距离为:",Ld) #显示所有顶点对之间的最短距离
print("顶点0到顶点4的最短距离为:",Ld[0][4]) #显示一对顶点之间的最短距离
m,n=a.shape; dd=np.zeros((m,n))
for i in range(m):
for j in range(n): dd[i,j]=Ld[i][j]
print("顶点对之间最短距离的数组表示为:\n",dd) #显示所有顶点对之间最短距离
#np.savetxt('example4.txt',dd) #把最短距离数组保存到文本文件中
p=nx.shortest_path(G, weight='weight') #返回值是可迭代类型
dp=dict(p) #转换为字典类型
print("\n顶点对之间的最短路径为:", dp)
print("顶点0到顶点4的最短路径为:",dp[0][4])
顶点对之间的距离为: {0: {0: 0, 1: 1, 2: 2, 3: 3, 6: 4, 4: 6, 7: 6, 5: 9}, 1: {1: 0, 0: 1, 2: 2, 3: 3, 6: 5, 4: 6, 7: 7, 5: 9}, 2: {2: 0, 3: 1, 0: 2, 1: 2, 4: 4, 6: 6, 5: 7, 7: 8}, 3: {3: 0, 2: 1, 1: 3, 4: 3, 0: 3, 5: 6, 6: 6, 7: 8}, 4: {4: 0, 3: 3, 6: 3, 5: 4, 2: 4, 7: 5, 1: 6, 0: 6}, 5: {5: 0, 4: 4, 7: 4, 3: 6, 6: 6, 2: 7, 1: 9, 0: 9}, 6: {6: 0, 7: 2, 4: 3, 0: 4, 1: 5, 5: 6, 3: 6, 2: 6}, 7: {7: 0, 6: 2, 5: 4, 4: 5, 0: 6, 1: 7, 3: 8, 2: 8}}
顶点0到顶点4的最短距离为: 6
顶点对之间最短距离的数组表示为:
[[0. 1. 2. 3. 6. 9. 4. 6.]
[1. 0. 2. 3. 6. 9. 5. 7.]
[2. 2. 0. 1. 4. 7. 6. 8.]
[3. 3. 1. 0. 3. 6. 6. 8.]
[6. 6. 4. 3. 0. 4. 3. 5.]
[9. 9. 7. 6. 4. 0. 6. 4.]
[4. 5. 6. 6. 3. 6. 0. 2.]
[6. 7. 8. 8. 5. 4. 2. 0.]]
顶点对之间的最短路径为: {0: {0: [0], 1: [0, 1], 2: [0, 2], 4: [0, 2, 3, 4], 6: [0, 6], 7: [0, 6, 7], 3: [0, 2, 3], 5: [0, 2, 3, 5]}, 1: {1: [1], 0: [1, 0], 2: [1, 2], 3: [1, 3], 7: [1, 7], 4: [1, 3, 4], 6: [1, 0, 6], 5: [1, 3, 5]}, 2: {2: [2], 0: [2, 0], 1: [2, 1], 3: [2, 3], 4: [2, 3, 4], 5: [2, 3, 5], 6: [2, 0, 6], 7: [2, 0, 6, 7]}, 3: {3: [3], 1: [3, 1], 2: [3, 2], 4: [3, 4], 5: [3, 5], 0: [3, 2, 0], 7: [3, 4, 6, 7], 6: [3, 4, 6]}, 4: {4: [4], 0: [4, 3, 2, 0], 2: [4, 3, 2], 3: [4, 3], 5: [4, 5], 6: [4, 6], 1: [4, 3, 1], 7: [4, 6, 7]}, 5: {5: [5], 3: [5, 3], 4: [5, 4], 6: [5, 6], 7: [5, 7], 0: [5, 3, 2, 0], 2: [5, 3, 2], 1: [5, 3, 1]}, 6: {6: [6], 0: [6, 0], 4: [6, 4], 5: [6, 5], 7: [6, 7], 1: [6, 0, 1], 2: [6, 0, 2], 3: [6, 4, 3]}, 7: {7: [7], 0: [7, 6, 0], 1: [7, 1], 5: [7, 5], 6: [7, 6], 4: [7, 6, 4], 3: [7, 6, 4, 3], 2: [7, 6, 0, 2]}}
顶点0到顶点4的最短路径为: [0, 2, 3, 4]