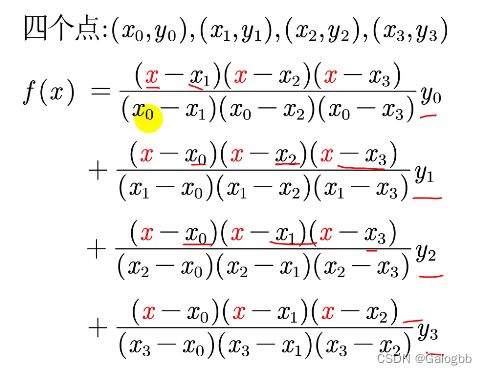数学建模学习笔记 | 插值算法
目录
前言
一、插值算法应用背景
二、一维插值
1.插值目标
2.传统插值方法
1.多项式的插值方法
2.拉格朗日插值法
3.分段插值(最常用)
4.牛顿插值
3.常用插值方法
1.埃尔米特插值
2.分段三次埃尔米特插值
3.三次样条插值
三.n维数据插值
总结
参考
前言
本文介绍几种常见的插值方法
一、插值算法应用背景
在数学建模的比赛中,通常要处理由试验、测量得到的大量数据或者一些过于复杂而不便于计算的函数表达式,然而有时候我们得到的数据是很少的,不可以进行数据的分析运算,这时候就需要模拟产生一些新的可靠的数据来满足我们的需求,这种方法是插值。其中在插值算法中,一维插值为一个x对应一个y,而多维插值则是多个x对应多个y
二、一维插值
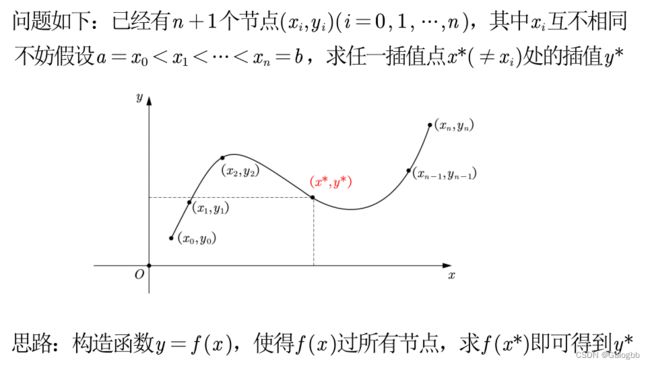
1.插值目标
构造出一个简单函数经过我们现知道的所有点,这个函数是不唯一的,如下图所示为其中一种插值方法,黑色的点为我们已知的所有点,红色的点为我们预测的点
2.传统插值方法
为了满足以上的目标,有以下三种实现的方法:
- 代数多项式插值
- 分段插值
- 三角插值
1.多项式的插值方法
定理:存在唯一的多项式!!!
Ps:
只要n+1个节点互不相同,则该条件的n阶多项式唯一
如果不限制多项式即n的次数,插值多项式不唯一,也就是说可以更曲折
2.拉格朗日插值法
数学解释
用法例子说明:
规律:整体x分别与不同的y相乘然后相加,整体的x分子为x未知数分别与剩下的点相减后相乘法,分母为该点的x值分别与剩下的点相减后相乘法
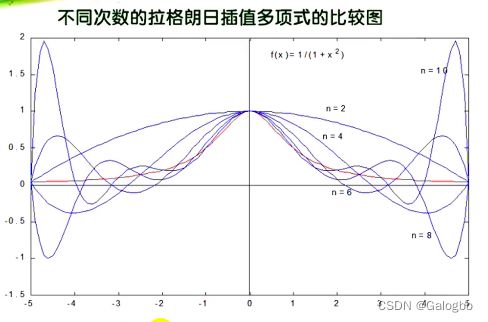
缺点-龙格现象
红色为原来的函数,蓝色为预测的,由图可知,n的次数越高,他的尾部震荡越大,因此一般不熟悉运动趋势的情况下,不要轻易用高次插值,为了减低龙格现象,因此引入了分段思想
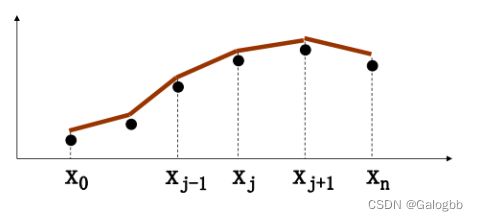
3.分段插值(最常用)
由于多项式次数高精度不一定高,而且误差可能会比较大,因此采用分段低次插值,也就是说按照几个点几个点的来预测一段一段的函数,然后拼接在一起
- 分段线性插值
两个点连在同一条直线上,然后预测中间所包含的值,但是又不准的地方
- 分段二次插值
三个点组成二次函数,然后再拼接在一起,组成新的函数进行预测
4.牛顿插值
找一个n次多项式,但是和拉格朗日不一样,加入了差商,减少了计算量,都是在前一项进行差商具有继承性,但是都存在龙格现象,这两种插值方法不能全面的反映被插函数的性态,缺乏导数值,因此很少用
3.常用插值方法
1.埃尔米特插值
2.分段三次埃尔米特插值
直接使用埃尔米特插值得到的多项式次数较高,也存在龙格线性,因此往往使用三次埃尔米特插值
操作如下:在matlab中有内置函数pchip
% 分段三次埃尔米特插值
x = -pi:pi; y = sin(x);
new_x = -pi:0.1:pi;
p = pchip(x,y,new_x);
figure(1); % 在同一个脚本文件里面,要想画多个图,需要给每个图编号,否则只会显示最后一个图哦~
plot(x, y, 'o', new_x, p, 'r-')3.三次样条插值
三次样条插值不仅仅要求二阶连续,而且还要求三阶连续
操作如下:在matlab中有内置函数spline
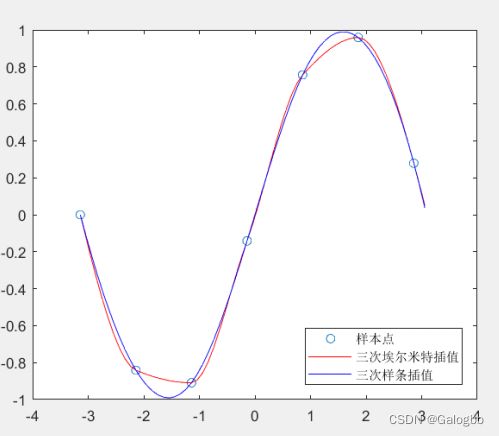
% 三次样条插值和分段三次埃尔米特插值的对比
x = -pi:pi;
y = sin(x);
new_x = -pi:0.1:pi;
p1 = pchip(x,y,new_x); %分段三次埃尔米特插值
p2 = spline(x,y,new_x); %三次样条插值
figure(2);
plot(x,y,'o',new_x,p1,'r-',new_x,p2,'b-')
legend('样本点','三次埃尔米特插值','三次样条插值','Location','SouthEast') %标注显示在东南方向效果比较
可以看出三次样条插值更加光滑,但是在实际项目中不确定函数的形状,因此两种插值都可以用
三.n维数据插值
操作方法:在matlab中有内置函数interpn
% n维数据的插值
x = -pi:pi; y = sin(x);
new_x = -pi:0.1:pi;
p = interpn (x, y, new_x, 'spline');
% 等价于 p = spline(x, y, new_x);
figure(3);
plot(x, y, 'o', new_x, p, 'r-')
Ps:可以验证一维插值
总结
以上就是今天要讲的内容,本文仅仅简单介绍了插值的几种常见方法,除了插值还有拟合,持续更新
参考
清风数学建模系列视频