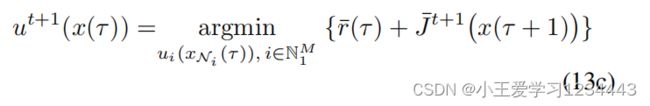论文研读笔记(三)——基于障碍函数的移动机器人编队控制安全强化学习
基于障碍函数的移动机器人编队控制安全强化学习(Barrier Function-based Safe Reinforcement Learning for Formation Control of Mobile Robots)
最近我在学习多机器人编队导航的论文,此篇文章为“X. Zhang, Y. Peng, W. Pan, X. Xu and H. Xie, “Barrier Function-based Safe Reinforcement Learning for Formation Control of Mobile Robots,” 2022 International Conference on Robotics and Automation (ICRA), 2022, pp. 5532-5538, doi: 10.1109/ICRA46639.2022.9811604.”的论文学习笔记,只供学习使用,不作商业用途,侵权删除。并且本人学术功底有限,如果有思路不正确的地方欢迎批评指正!
摘要
分布式模型预测控制(DMPC)关注如何有效地在线控制多个有约束的机器人系统。然而,动态系统模型和约束的非线性、非凸性和强互连可以使实时和现实世界的 DMPC 实现变得不平凡。强化学习 (RL) 算法有望用于控制策略设计。然而,如何在 RL 的状态约束方面确保安全仍然是一个重要问题。提出一种基于障碍函数的安全强化学习算法,用于状态约束下的非线性多机器人系统DMPC。所提出的方法由几个基于本地学习的 MPC 监管机构组成。每个与本地系统相关联的调节器都使用安全的强化学习算法以分布式方式学习和部署本地控制策略,即仅在相邻代理之间使用状态信息。作为所提出算法的一个突出特点,文中提出了一种新颖的基于障碍的策略结构来确保安全,该结构具有清晰的机制解释。具有防撞功能的移动机器人的编队控制的模拟和真实世界实验都表明了所提出的 DMPC 安全强化学习算法的有效性。
介绍
近年来,多机器人系统的分布式模型预测控制(DMPC)在[1]-[3]系统中受到了广泛的关注。与集中控制解决方案相比,分布式控制结构更高效、可扩展、维护[4]更友好。一个基于状态约束的多机器人控制的解决方案依赖于一个基于模型预测控制(MPC)[5],[6]的分布式结构。在这种情况下,许多DMPC方法被提出为[7]-[11],其中将局部MPC问题转化为几个优化问题,这些问题可以与邻居的信息交换并行在线解决。这样的过程需要定期访问本地的板载计算资源。为了减少计算负担,提出了一种显式分布式MPC算法[12],该算法首先离线计算一组与标记的单独约束区域相关联的分段显式控制策略。然后,根据州所在的区域在线搜索控制策略。然而,该方法仅针对线性系统进行设计,并依赖于系统的可分性假设。
在不同的环境下,基于强化学习(RL)和自适应动态规划(ADP)的分布式解决方案在过去的几十年[13]-[19]也受到了极大的关注。在基于RL的分布式方法中,RL和ADP通常依赖于参与者-批评结构,以正向的方式学习无限水平最优控制问题的近最优控制策略。与DMPC相比,分布式RL方法[13]-[19]可以更有效地解决优化问题。此外,由此产生的控制策略可以离线学习和在线部署,大大减少了计算负载。鉴于关键特征,演员-批评强化学习被用于一种后退的方式来学习[20]-[22]中集中式MPC的显式控制策略。在本文中,文中将工作[20]-[22]扩展到多代理的分布式控制场景。
至关重要的是,在许多安全关键分布式控制应用中,状态约束是一项困难的任务,也是一项艰巨的任务,也是不可或缺的要求。据作者所知,这个问题在上述基于学习的MPC[20]、[21]和RL算法[13]-[19]、[23]、[24]中还没有得到解决。在[25]中,提出了一种用于多机器人运动规划的安全强化学习算法。利用基于李亚普诺夫障碍的代价函数整形方法的代价函数,利用脉冲势场重建代价函数。然而,这种成本函数塑造处理可能会引入成本函数梯度的突变,容易导致行为者网络和批评者网络的权值的发散行为。
本文提出了一种基于屏障函数的非线性多机器人系统,针对分布式MPC(DMPC)的安全强化学习(BSRL)方法,称为SL-DMPC。该方法由几个基于BSRL的MPC调节器组成。每个调节器与本地系统相关联,以分布式的方式使用BSRL算法学习和部署本地MPC策略,即只在邻居代理之间进行状态信息交换。请注意,如何保证在国家约束下学习安全在强化学习社区仍然是一个挑战。在提出的BSRL算法中,不同于[25],[27],[28]不同,文中提出了一种新的基于障碍的控制策略结构,以保证状态约束下的学习安全,它对安全证书有清晰的机制解释。
与带有数值解的DMPC不同,SL-DMPC的实现依赖于几种基于障碍的行为评论家RL算法,为每个代理生成一个局部显式的状态反馈控制策略,而不是使用策略梯度的开环控制序列。这些本地控制策略可以同步学习和部署,也可以离线学习并在线部署。此外,还证明了基于屏障的强化学习算法在每个预测领域的安全保证。通过了模拟和真实的移动机器人编队控制实验,证明了所提出的SL-DMPC的有效性。
本文的其余部分组织如下。第二节介绍了线性动力系统的问题公式和DMPC的初步介绍。在第三节中,提出了针对非线性系统的SLDMPC算法。并对其进行了理论分析。在第四节中,演示了移动机器人非线性编队控制的仿真和实际实验结果。结论见第五节。
符号:文中使用 N l 1 l 2 \mathbb{N} _{l_1}^{l_2} Nl1l2来表示整数 l 1 , l 1 + 1 , … , l 2 l_1,l_1+1,\dots ,l_2 l1,l1+1,…,l2的集合。对于一组载体 z i ∈ R n i , i ∈ N 1 M z_i\in\mathbb{R} ^{n_i},i\in\mathbb{N}_1^M zi∈Rni,i∈N1M,文中使用 c o l i ∈ N 1 M ( z i ) {\rm col}_{i\in\mathbb{N}_1^{M(z_i)}} coli∈N1M(zi)表示 [ z 1 T , … , z M T ] T [z_1^{\rm T},\dots ,z_M^{\rm T}]^{\rm T} [z1T,…,zMT]T,其中 M M M是一个整数。文中使用 u ( k ) u(k) u(k)表示由控制序列 u ( k ) , … , u ( k + N − 1 ) u(k),\dots ,u(k+N-1) u(k),…,u(k+N−1)形成的控制策略,其中 N N N为MPC的预测范围, k k k为离散时间指数。
对DMPC的问题制定和初步研究
A.问题表述
所控制的整个系统由 M M M个离散时间、非线性、相互作用的子系统组成,描述为:
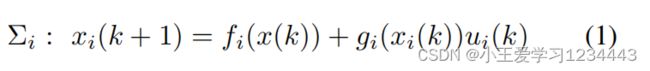
对于 ∀ N i M \forall \mathbb{N}_i^M ∀NiM,其中 x i ∈ χ i ⊆ R n i x_i\in\chi _i\subseteq \mathbb{R}^{n_i} xi∈χi⊆Rni和 u i ⊆ R m i u _i\subseteq \mathbb{R}^{m_i} ui⊆Rmi状态和输入变量与子系统 ∑ i {\sum}_i ∑i,而 k k k是离散时间指数, f i ∈ R n i f_i \in\mathbb{R}^{n_i} fi∈Rni和 g i ∈ R n i × m i g_i \in\mathbb{R}^{n_i\times m_i} gi∈Rni×mi平滑状态转换和输入映射函数和 f i ( 0 ) = 0 f_i(0)=0 fi(0)=0。本地状态集被定义为 χ i = { x i ∈ R ∣ B i t ( x i ) ≤ 0 , t ∈ N 1 q i } \chi _i=\{x_i\in \mathbb{R}|B_i^t(x_i)\le0,t\in \mathbb{N}^{q_i}_1\} χi={xi∈R∣Bit(xi)≤0,t∈N1qi}, i ∈ N 1 M i \in \mathbb{N}^M_1 i∈N1M, B i t B_i^t Bit是一个 C 1 C_1 C1函数,和 χ = χ 1 × ⋯ × χ M \chi=\chi_1\times\dots\times\chi_M χ=χ1×⋯×χM。
从(1)收集所有子系统,整体集中的动态模型,记为 ∑ \sum ∑,可以写为:
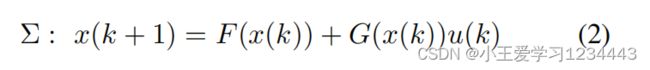
其中 x = c o l i ∈ N 1 M ( x i ) ∈ R n x={\rm col}_{i\in\mathbb{N}_1^M}(x_i)\in\mathbb{R}^n x=coli∈N1M(xi)∈Rn, n = ∑ i = 1 M n i n={\sum}_{i=1}^Mn_i n=∑i=1Mni, u = c o l i ∈ N 1 M ( u i ) ∈ R m u={\rm col}_{i\in\mathbb{N}_1^M}(u_i)\in\mathbb{R}^m u=coli∈N1M(ui)∈Rm, m = ∑ i = 1 M m i m={\sum}_{i=1}^Mm_i m=∑i=1Mmi, F = ( f 1 , … , f M ) F=(f_1,\dots,f_M) F=(f1,…,fM), G G G的对角线块是输入矩阵 g i g_i gi, i ∈ N 1 M i\in\mathbb{N}^M_1 i∈N1M。现在文中给出了一个多机器人系统中的邻居子系统的定义。
定义1(邻居子系统):对于子系统 ∑ i {\sum}_i ∑i,状态 x j x_j xj是 ∑ i {\sum}_i ∑i的邻居状态如果 x j a x^a_j xja, x j b x^b_j xjb当 x j b ≠ x j b x^b_j\ne x^b_j xjb=xjb表示 f i f_i fi值不同,则状态 x i x_i xi是邻居状态。状态xNi∈RnNi是所有相邻态的集合,即xNi=colj∈Nixj,其中Ni是与相邻态相关的所有指标j的集合。
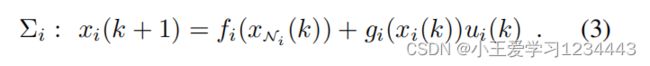
下面文中给出了下面对机器人之间的通信协议的假设:
假设1(通信协议):允许相邻子系统之间的通信,即如果i∈Nj或j∈Ni,状态信息可以在Σi和Σj之间进行双向交换。
本文考虑的控制目标是将x(k)→0和u(k)→0驱动为k→+∞,同时对所有i∈NM1强制执行局部状态约束xi(k)∈Xi。
B.线性系统的DMPC的初步研究
鉴于MPC具有明确处理状态约束的能力,DMPC可以很自然地用于解决所考虑的多机器人控制问题。首先,让文中回顾一下线性系统的DMPC公式[29]。在每个时间步长 k k k处,应尽量减少以下有限视界合作代价函数:
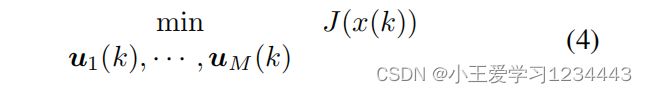
其中,全局成本 J J J被定义为:
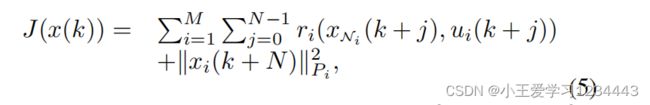
具有代价(5)的(4)中的优化问题可以通过模型(2)、局部状态约束 x i ( k + j ) ∈ χ i , ∀ j ∈ N 1 N , i ∈ N 1 M x_i(k+j)\in\chi_i,\forall j\in\mathbb{N}_1^N,i\in\mathbb{N}_1^M xi(k+j)∈χi,∀j∈N1N,i∈N1M进行数值求解。这个问题可以通过数值优化工具以分布式的方式来解决,参见[29],[30],因为局部状态约束是解耦的。因此,可以为每个预测范围中的每个代理计算局部开环控制序列。与在动态规划的过程中一样,应用第一个控制动作,并在下一个时刻重复求解(4)。
C.屏障功能和安全控制的定义
文中引入了基于状态约束的障碍函数的定义,并在基于障碍函数的强化学习算法中用于状态约束的满足。定义2(势垒函数):对于任何集合 χ i , i ∈ N 1 M \chi _i,i\in\mathbb{N}^M_1 χi,i∈N1M,一个势垒函数被定义为:
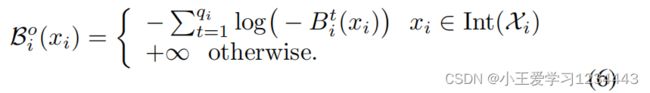
定义3(预测范围内的安全控制):在一般时间k时,一个记为 u ( k ) u(k) u(k)的控制策略,如果所得到的状态演化满足 x ( k + 1 ) , … , x ( k + N ) ∈ χ n x(k+1),\dots,x(k+N)\in\chi^n x(k+1),…,x(k+N)∈χn,则对(2)是安全的.
基于屏障函数的DMPC安全强化学习
由于动态系统模型(1)是非线性甚至非凸的,因此使用像(4)这样的DMPC来解决所考虑的多机器人控制问题不是平凡的。本节提出了一种基于障碍函数的安全强化学习算法来求解DMPC,即SL-DMPC,以分布式的方式学习每个代理的局部状态反馈控制策略。在第三节-A中,文中首先提出了SL-DMPC的主要思想,其中使用了一个基于屏障函数的控制策略来处理状态约束。并给出了该方法的安全保证和收敛性分析。在第三-B节中,提出了基于屏障函数的强化学习算法来实现SL-DMPC。
A.SL-DMPC的设计
设计一个解决DMPC的RL算法的主要困难在于保证在局部状态约束下的安全。为了解决这个问题,在SL-DMPC中,文中提出了一个基于屏障函数的控制策略结构来保证安全性。为此,文中首先用障碍函数重建性能指标J,即:
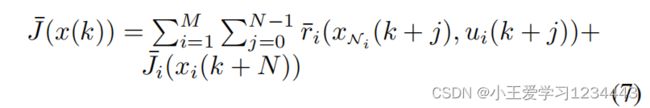
其中阶段的花费是:
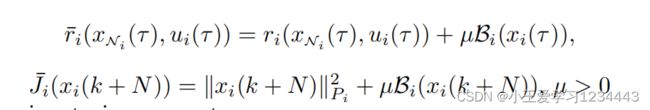
是一个调优参数。以集体形式,对于任何 τ ∈ [ k , k + N − 1 ] τ∈[k,k+N−1] τ∈[k,k+N−1],都可以编写:
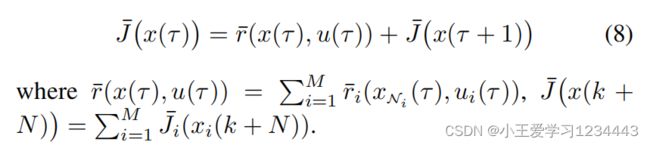
为了以分布式的方式优化(8),文中为子系统 Σ i Σ_i Σi构建了一个基于本地屏障的控制策略:
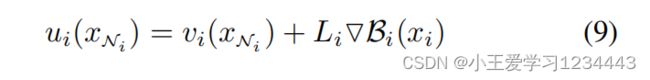
其中, v i ∈ R m i v_i∈\mathbb{R}^{m_i} vi∈Rmi是一个新的虚拟控制策略,而 L i ∈ R m i × n i L_i∈\mathbb{R}^{m_i\times n_i} Li∈Rmi×ni是一个需要进一步优化的决策变量(在第三节的B中延迟)。
备注1:(9)中的第二项是产生与第i个代理相关的局部排斥力,它随着状态 x i x_i xi向 χ i \chi_i χi的边界移动而增长。通过这样做,可以限制局部状态 x i x_i xi的内部,即通过(9)中状态约束的屏障函数的梯度来保证安全。
在任意时间即时 τ ∈ [ k , k + N − 1 ] τ∈[k,k+N−1] τ∈[k,k+N−1],设 J ˉ ∗ ( x ( τ ) ) \bar J^∗(x(τ)) Jˉ∗(x(τ))为控制结构(9)下的最优值函数,则可以将离散时间HJB方程写为:
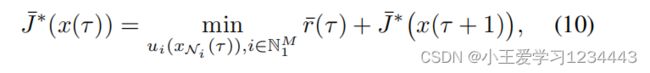
对于每个局部最优控制策略:
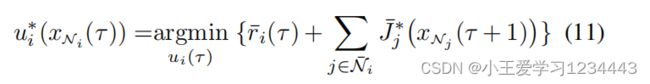
对于 i ∈ N 1 M i∈N^M_1 i∈N1M,其中 N ˉ i \bar N_i Nˉi是子系统的集合与其相邻的子系统的集合。
与经典的数值优化方法不同,文中采用下面的SL-DMPC算法来求解(10)和(11),见算法1。

在下面的定理中,文中证明了在每个预测范围内,(12)中的控制策略是安全的(见定义3),并且控制策略和值函数最终也将分别收敛到它们的最优值,即:
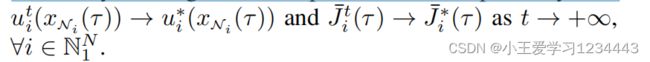
定理1(安全保证和收敛性):设u0(k)是安全策略,为初值函数。
![]()
证明. 1: 首先,通过收集所有i∈NM1的迭代步骤(12a),将得到以下集中的形式:
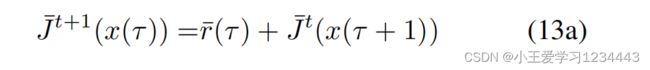
此外,由于 u i u_i ui只与 x N i 相 x_{N_i}相 xNi相关,因此(12b)等价于:
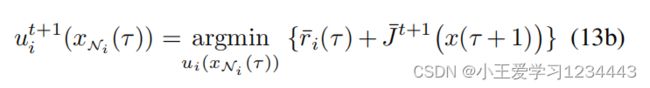
然后,文中可以将[31]中的证明参数应用于集中式系统,从而证明了这一点。
J ˉ t + 1 ( x ( τ ) ) ≤ V t ( x ( τ ) ) ≤ J ˉ t ( x ( τ ) ) , ∀ τ ∈ [ k , k + N − 1 ] \bar J^{t+1}(x(τ )) ≤ V^t(x(τ )) ≤ \bar J^t(x(τ )), \forall τ ∈ [k, k + N − 1] Jˉt+1(x(τ))≤Vt(x(τ))≤Jˉt(x(τ)),∀τ∈[k,k+N−1]
此外,根据[31],第二点和第三点可以很自然地得到证明。有兴趣的读者可以参考[31]了解更多细节。
B.基于RL的分布式边界函数的DMPC
下面,算法1将使用基于行为评论家框架[16]的基于分布式屏障函数的RL算法来实现。与DMPC的数值解相比,这种实现的优点是为每个代理生成一个局部显式的状态反馈控制策略,而不是一个开环控制序列。这允许直接离线部署学习到的控制策略。所提出的基于分布式屏障的RL由 M M M个行为评论家网络对组成,每个网络对为每个局部代理设计,以学习局部控制策略和相邻代理之间信息交换的值函数。对于任何子系统 i ∈ N 1 M i∈\mathbb{N}^M_1 i∈N1M,批评者网络被构建为:
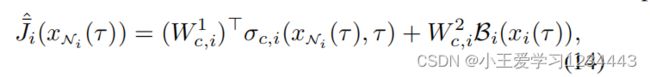
其中 W 1 c , i ∈ R N c , i × n i W^1{c,i}∈\mathbb{R}^{N_{c,i}×n_i} W1c,i∈RNc,i×ni是加权矩阵, σ c , i ∈ R N c , i σ_{c,i}∈\mathbb{R}^{N_{c,i}} σc,i∈RNc,i是一个由激活函数组成的向量。
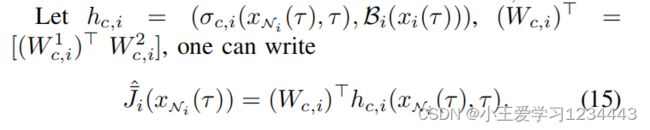
为了最小化 J ˉ i ∗ \bar J^∗_i Jˉi∗和 J ˉ ^ i \hat{\bar{J} }_i Jˉ^i之间的偏差,鉴于(12a),文中将以下 J ˉ i d \bar J^d_i Jˉid定义为 J ˉ ^ i \hat{\bar{J} }_i Jˉ^i的期望值,如下:
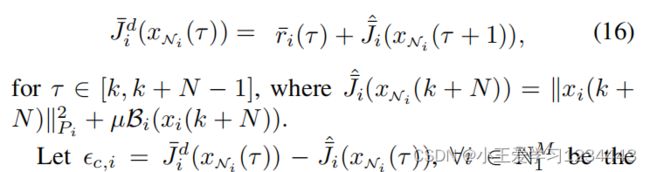
为局部近似误差。以下是每个 i ∈ N 1 M i∈N^M_1 i∈N1M的二次代价要最小化,即,
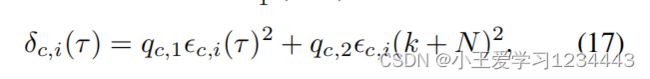
其中 q c , 1 , q c , 2 > 0 q{c,1},q_{c,2}>0 qc,1,qc,2>0是调优参数。最小化(17)导致加权矩阵 W c , i W_{c,i} Wc,i的更新规则为:
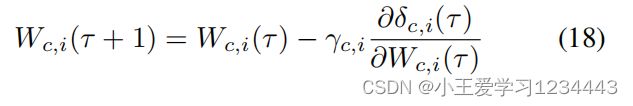
其中, γ c , i γ_{c,i} γc,i为局部学习率。
同样地,文中为每个代理构造基于屏障的参与者,即,
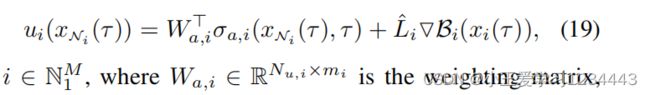
为加权矩阵,其中 σ a , i ∈ R u N σ_a,i∈\mathbb{R}^N_u σa,i∈RuN, i i i是一个由激活函数组成的向量, L ^ i ∈ R m i × n i \hat{L}_i∈\mathbb{R}^{mi×ni} L^i∈Rmi×ni是 L i L_i Li的近似值。针对(12b),文中设计了一个期望的 u i ( τ ) u_i(τ) ui(τ)值,即 u i d ( τ ) u_i^d(τ) uid(τ)为
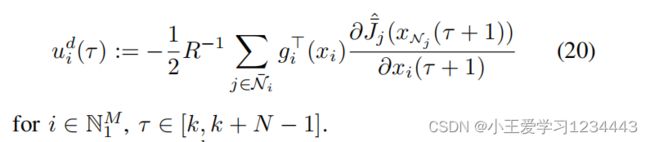
设 ϵ a , i ( τ ) = u i d ( τ ) − u i ( τ ) \epsilon _{a,i}(τ)=u^d_i(τ)−u_i(τ) ϵa,i(τ)=uid(τ)−ui(τ),其中 ϵ a , i \epsilon _{a,i} ϵa,i是近似误差。在每次即时 τ ∈ [ k , k + N − 1 ] τ∈[k,k+N−1] τ∈[k,k+N−1],每个代理最小化 ϵ a , i ( τ ) \epsilon_{a,i}(τ) ϵa,i(τ),即, δ a , i ( τ ) = ∥ ϵ a , i ( τ ) ∥ δ_{a,i}(τ)=\left \| \epsilon_{a,i}(τ) \right \| δa,i(τ)=∥ϵa,i(τ)∥,导致 W a , i W_{a,i} Wa,i和 L ^ i \hat L_i L^i的更新规则
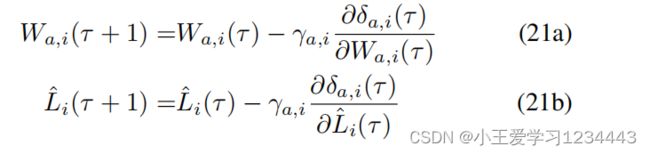
其中, γ a , i γ_{a,i} γa,i为局部学习率。
所提出的基于分布式屏障函数的安全RL算法在每个预测范围 [ k , k + N ] [k,k+N] [k,k+N]内的学习步骤可以总结如下。对于 τ = k , k + 1 , ⋅ ⋅ ⋅ , k + N − 1 τ=k,k+1,···,k+N−1 τ=k,k+1,⋅⋅⋅,k+N−1,重复执行以下步骤:
- 使用(1)生成 x i ( τ + 1 ) x_i(τ + 1) xi(τ+1), ∀ i ∈ N 1 M ∀i ∈ \mathbb{N}^M_1 ∀i∈N1M
- 用(16)和(20)计算 J ^ i d ( x N i ( τ ) ) \hat{J}_i^d(x_{N_i}(τ)) J^id(xNi(τ))和 u i d ( τ ) u^d_i(τ) uid(τ)使用 x N i ( τ + 1 ) x_{N_i}(τ+1) xNi(τ+1)和 x j ( τ ) x_j(τ) xj(τ),对于所有 j ∈ N i j∈N_i j∈Ni。
- 并行更新 W c , i ( τ + 1 ) W_{c,i}(τ+1) Wc,i(τ+1)与(18)和 W a , i ( τ + 1 ) W_{a,i}(τ+1) Wa,i(τ+1), L ^ i ( τ + 1 ) \hat L_i(τ+1) L^i(τ+1)与(21)。
在预测范围 [ k , k + N ] [k,k+N] [k,k+N]的学习过程后,将用(20)计算的第一个控制动作 u i ( x N i ( k ) ) u_i(x_{N_i}(k)) ui(xNi(k))应用于(1)。然后在随后的预测视界 [ k + 1 , k + N + 1 ] [k+1,k+N+1] [k+1,k+N+1],重复上述学习过程。
**备注2:**请注意,RL算法的训练过程(18)和(21)只使用了部分模型信息 G ( x ) G(x) G(x)。以一种稍微不同的方式,可以改变局部批评者根据双启发式规划[32]估计局部状态 λ i = ∂ J ˉ i ( x N i ) / ∂ x N i λ_i=∂\bar{J}_i(x_{N_i})/∂x_{N_i} λi=∂Jˉi(xNi)/∂xNi的作用,它可以通过利用模型信息 F ( x ) F(x) F(x)来加快收敛过程。
**备注3:**应该强调的是,基于分布式屏障函数的RL算法以完全分布式的方式训练和部署,即状态信息沟通在每个训练时间即时权重更新的评论家和在每个部署时间即时实现分布式控制。
现在文中将对计算复杂性问题进行了一些讨论。如果使用像[33]这样的快速局部MPC实现,则经典分布线性MPC的计算复杂度约为 O ( M N ( n N i + m i ) n N i 2 ) O(MN(n_{N_i}+m_i)n^2_{N_i}) O(MN(nNi+mi)nNi2)。在训练过程中,文中的方法的主要计算复杂度是对(18)、(21)和前向模型预测的更新,这大致是线性系统的 O ( M N ( n c , i + n u , i + n N i ) n N i 2 ) O(MN(n_{c,i}+n_{u,i}+n_{N_i})n^2_{N_i}) O(MN(nc,i+nu,i+nNi)nNi2)。当直接部署学习到的控制策略时,即使对于非线性多机器人系统,整体在线计算复杂度也降低到 O ( M ( n u , i n N i ) ) O(M(n_{u,i}n_{N_i})) O(M(nu,inNi))。总之,总体计算复杂度随着要去的代理的数量呈线性增长。
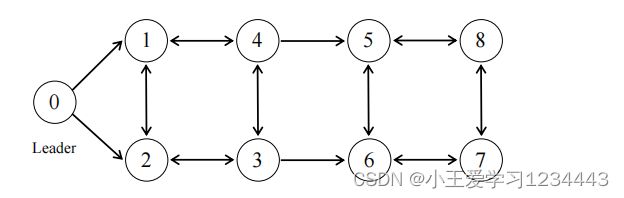
移动机器人的通信图如下,其中箭头表示移动机器人的信息传输方向,机器人0为领先机器人。
移动机器人编队控制的仿真与实验结果
A.模拟实验
考虑 M ( M = 8 ) M(M=8) M(M=8)移动机器人的编队控制。本地移动机器人之间的通信有向图如图1所示。第i个机器人的运动学模型为
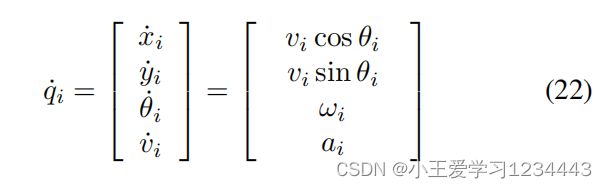
式中 ( x i , y i ) (x_i,y_i) (xi,yi)为笛卡尔坐标系中第i个机器人的坐标, θ i θ_i θi和 v i v_i vi分别为偏航角和线速度, u i = [ a i , ω i ] T u_i=[a_i,ω_i]^{\rm T} ui=[ai,ωi]T为控制输入,其中 a i a_i ai和 ω i ω_i ωi分别为加速度和偏航率。
让文中将第 i i i个机器人在局部坐标系中的形成误差定义为
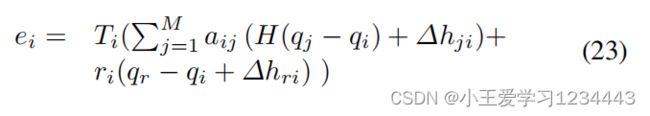
其中, a i j = 0 , 1 a_{ij}=0,1 aij=0,1表示连接状态,如果机器人 i i i从机器人 j j j接收到状态信息,否则, a i j = 0 a_{ij}=0 aij=0; r i r_i ri表示钉扎增益, r i = 1 r_i=1 ri=1表示机器人我能接收到领导者的信息, H = d i a g { 1 , 1 , 0 , 0 } H={\rm diag}\{1,1,0,0\} H=diag{1,1,0,0}。 ∆ h j i ∆h_{ji} ∆hji和 ∆ h r i ∆h_{ri} ∆hri是坐标校正变量,由地层形状和大小决定;坐标变换矩阵为
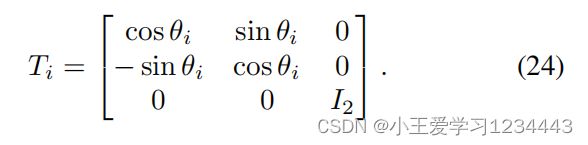
通过在变换(23)下离散(22),可以将离散时间局部形成误差模型写为
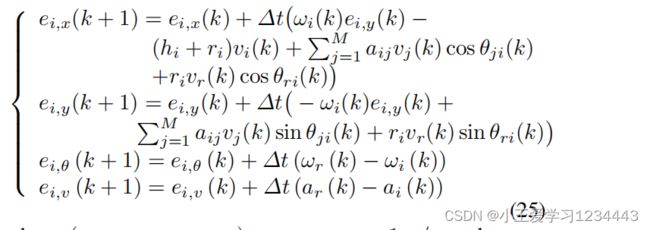
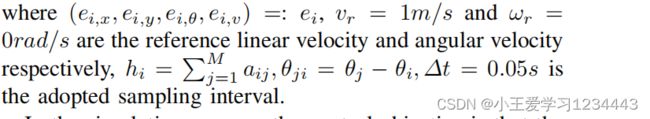
在仿真过程中,控制目标是移动机器人可以沿四行两列矩形的直线,避免路径上的障碍(见图2),同一行与列中相邻移动机器人之间的期望距离分别为2m和1m。所有需要避免的障碍物均为直径为0.5m的圆形物体(另见图2)。两个障碍物的坐标分别为(0,2)和(25,0)。在提出的SL-DMPC中,将惩罚矩阵选为 Q n N i = I n N i Q_{n_{N_i}}=I_{nN_i} QnNi=InNi, R i = I 2 R_i=I_2 Ri=I2,预测范围设为N=20。在训练过程中,将参与者和批评者的权重矩阵设置为均匀分布的随机值,并根据(18)和(21)在每个时间时刻进行更新。模拟是在英特尔酷睿[email protected]的笔记本电脑上使用MATLAB进行的。
下图的仿真结果表明,移动机器人可以从无序的初始状态条件下实现一个预定义的地层形状,同时避免了路径上遇到的所有障碍物,并在避碰后恢复了地层形状。从图2中可以观察到每个局部机器人的形成误差收敛于原点。

在仿真测试中,对8个具有防撞功能的移动机器人进行编队控制,其中黑色圆形区域(直径0.5m)代表障碍物,彩色线代表移动机器人的运动轨迹,同时同一列中的移动机器人用相同的彩色点标记。
B.现实世界的实验
文中还在两个真实的移动机器人上测试了文中提出的算法,用于防碰撞的地层控制(见下图)。在实验中,文中直接部署了离线学习到的局部策略来控制本地移动机器人。在每个采样时刻,机载卫星惯性制导集成定位系统测量每个本地状态 q i , i = 1 , 2 q_i,i=1,2 qi,i=1,2。测量到的 q 1 q_1 q1和相应的参考 q r q_r qr通过无线电从第一个机器人传输到第二个机器人。此外,将测量到的 q 2 q_2 q2从第二个机器人传输到第一个机器人。每个机器人都配备了一台笔记本电脑,其中安装了Unbuntu操作系统。在每台笔记本电脑中,利用测量的状态信息实时计算控制输入。采样间隔设为 ∆ t = 0.1 ∆t=0.1 ∆t=0.1s。
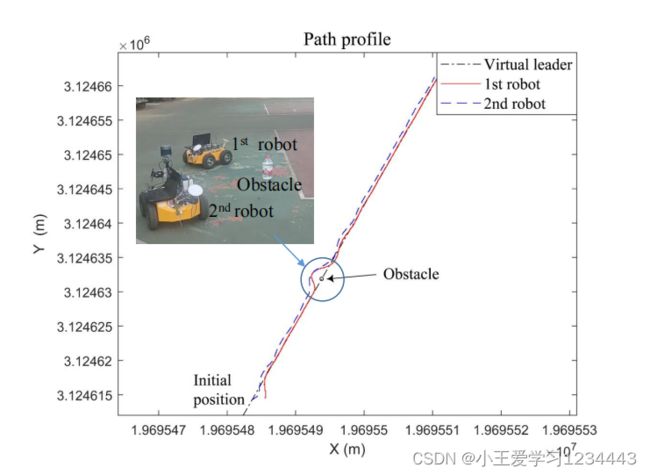
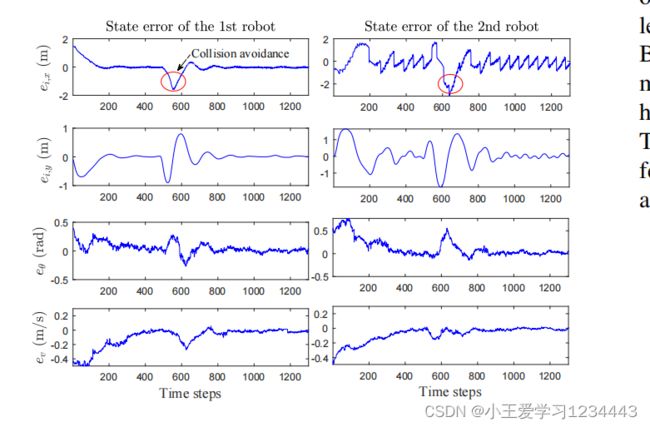
在实验中,文中在参考路径上添加了一个静态障碍。第一个机器人有望避开障碍物。为了简化实验设置,文中假设障碍物的位置信息是预先检测到的计算机视觉算法。在局部避碰条件下的实验结果如图3和图4所示,结果表明,移动机器人能够成功地避开障碍物1。同时,即使在避碰过程中,也保持了地层形状。请注意,在构建的软件中,测量状态和从无线电接收的状态之间存在明显的异步问题,这可能导致不可忽视的不确定性。即便如此,在这种情况下,文中的算法也显示出了很强的鲁棒性(参见下图)。
结论
本文提出了一种基于屏障函数的安全强化学习方法,用于具有状态约束的非线性多机器人系统的分布式模型预测控制(即SL-DMPC)。与经典的DMPC算法不同,SL-DMPC的实现依赖于一个基于参与者-批评者框架的分布式安全强化学习算法,从而为每个代理产生一个局部显式的状态反馈控制策略,而不是一个开环控制序列。这些本地控制策略可以同步学习和在线部署,也可以离线学习和在线部署,从而显著减少了有关DMPC的计算负载。作为另一个突出的特征,文中提出了一种新的基于屏障的控制策略结构,以保证分布式强化学习算法的安全性。此外,还证明了基于障碍函数的安全强化学习算法在每个预测领域的学习安全性和收敛性。对防撞移动机器人编队控制的模拟和真实实验结果验证了该方法的有效性。