机器学习技法 之 深度学习（Deep Learning）

前面学习了基础神经网络算法，可以得知神经网络基本结构中：神经元（Node）的个数，层数（Layer），以及激活函数的类型和神经元之间的连接形式都是可以自己选择的，这就导致结构的多样性，那么如何选择呢？当然是视情况而定了。

浅层与深层（Shallow versus Deep Neural Networks）

浅（shallow）层以为着较少（few）的隐含层（hidden layers）。其意味着：

• 训练效率高
• 简单的结构设计
• 理论上如果神经元足够多，那么就足够强，拟合任何问题

深层（deep）层以为着较少（few）的隐含层（hidden layers）。其意味着：

• 训练时间消耗大
• 复杂的结构设计
• 非常有力，可以拟合任何问题
• 更有意义

对于深度神经网络来说，由于层数较多，那每一层的任务相对来说比较简单，许多层完成一个复杂任务。并且常常用于一些使用原始特征比较困难的学习任务。

深度学习的挑战和关键技术（Challenges and Key Techniques）

difficult structural decisions:
结构设计困难

• subjective with domain knowledge: like convolutional NNet for
  images
  具有主观性，一般会结合专业知识进行设计，像卷积神经网络

high model complexity:
高模型复杂度

• no big worries if big enough data
  如果数据不够多会导致过拟合
• regularization towards noise-tolerant: like
  对噪声的容忍度提高
  • dropout (tolerant when network corrupted)，对网络出现问题导致噪声的容忍度
  • denoising (tolerant when input corrupted)，对输入噪声的容忍度

hard optimization problem:
很难优化

• careful initialization to avoid bad local minimum: called pre-training
  仔细选择初始值以防止不好的局部最优解，叫做预训练

huge computational complexity (worsen with big data):
高计算复杂度

• novel hardware/architecture: like mini-batch with GPU
  随着硬件的更新换代，这一问题得到缓和。

林老师认为这几条中初始化和正则化属于比较关键的技术。

二阶段深度学习框架（A Two-Step Deep Learning Framework）

第一阶段是：

$$\text{ for }\ell =1,\dots ,L.\text{ pre-train }\left\{w_{ij}^{(\ell )}\right\}\text{ assuming }{w}_{\ast }^{(1)},\dots w_{\ast }^{(\ell -1)}\text{ fixed }$$

什么意思呢，简单来说就是，先获得第一层的权重值，然后固定第一层的权重值来获得第二层的权重值，依次执行到最后一层。这一过程叫做预训练（pre-train)。可以看出这是一个多输入多输出问题（MIMO），但是丝毫不影响神经网络的训练，这是由于反向传播算法的实现，如果有不懂的话可以看前一篇《机器学习技法之神经网络》。

第二阶段是：

$$\text{ train with backprop on pre-trained NNet to fine-tune all }\left\{w_{ij}^{(\ell )}\right\}$$

即以预训练获取的权值作为初始值，然后使用反向传播算法进行迭代优化。

自编码器（Autoencoder）

信息保留式编码（Information-Preserving Encoding）

实际上每一层神经元的特征转换类似于编码过程（或者说转换表现形式），如果经过编码后，表现形式改变（different representation），但是代表的信息不变（same info）的话，便将之称为信息保留式编码（Information-Preserving Encoding）。所以经过信息保留式编码后的可以准确的解码为原来的表现形式。

那么现在的想法就是使用这种编码形式实现预训练，获取初始权值。

信息保留式神经网络（Information-Preserving Neural Net）

假设当前需求的神经网络只有一层隐含层，那么这种编码形式的神经网络结构图如下：

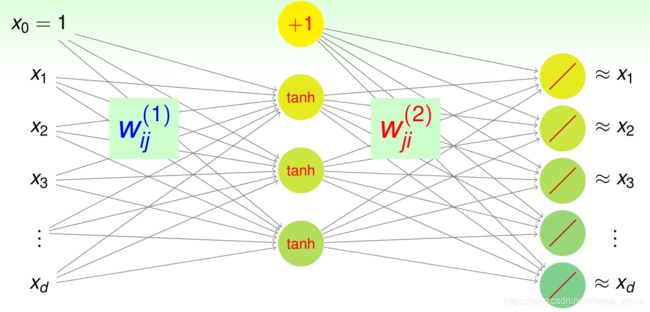
这种以 $d-\tilde{d}-d\text{ NNet with goal }{g}_i(\mathbf{x})\approx x_i$ 为结构形式的神经网络叫做自编码器（Autoencoder）。实际上就是在学习一个逼近恒等（自身）的函数（approximate identity function），identity 意思为将某个东西对应到它本身。

那么这次称编码权重（encoding weights）为：${\mathbf{w}}_{ij}^{(1)}$，解码权重（decoding weights）为：${\mathbf{w}}_{ij}^{(2)}$

逼近恒等函数（Approximating Identity Function）

这种函数的意义是：这种逼近过程会使用到（仰赖）一些已获得样本数据（observed data）中的隐藏结构（hidden structures），

对于监督学习，这种潜在的结构（hidden structure，比如说进行文字识别时学到的笔画）可以用于作为合理的特征转换 $\Phi (\mathbf{x})$（ reasonable transform）。这种潜在结构等于是原数据的信息表示（‘informative’ representation）。

对于无监督学习，自编码器更像是在学习数据的类型表示（‘typical’ representation of data）。在密度估计（density estimation）中，如果这类数据越多，那么这类数据的逼近越好，也就是自编码器的误差越少。在异常检测（outlier detection）中，如果自编码器的误差很小，那么代表该数据属于原来的训练数据。

所以说自编码器（autoencoder）是通过逼近恒等函数实现的一种表示学习（representation-learning through approximating identity function)。

基本的自编码器（Basic Autoencoder）

Basic Autoencoder 的表现形式为：

$$d-\tilde{d}-d\text{ NNet with error function }\sum _{i=1}^d{\left(g_i(\mathbf{x})-x_i\right)}^2$$

有以下特点：

1. backprop easily applies; shallow and easy to train
   反向传播算法容易应用，隐含层少易于训练
2. usually $d>\tilde{d}$ : compressed representation
   一般情况下隐含层神经元个数小于输入（或输出），从而达到一种数据压缩的效果
3. 数据的格式为：$\left\{\left({\mathbf{x}}_1,{\mathbf{y}}_1={\mathbf{x}}_1\right),\left({\mathbf{x}}_2,{\mathbf{y}}_2={\mathbf{x}}_2\right),\dots ,\left({\mathbf{x}}_N,{\mathbf{y}}_N={\mathbf{x}}_N\right)\right\}$，所以也被用于无监督学习（categorized as unsupervised learning technique）。
4. 有时候加入约束条件 $w_{ij}^{(1)}=w_{ji}^{(2)}$ 作为一种正则化，但是在计算梯度时会更复杂。

其中 $w_{ij}^{(1)}$ 用作预训练权重。

那么使用自编码器进行预训练的过程为：

第一阶段是：

$$\text{ for }\ell =1,\dots ,L.\text{ pre-train }\left\{w_{ij}^{(\ell )}\right\}\text{ assuming }{w}_{\ast }^{(1)},\dots w_{\ast }^{(\ell -1)}\text{ fixed }$$

$$\text{ by training basic autoencoder on }\left\{{\mathbf{x}}_n^{(\ell -1)}\right\}\text{ with }\tilde{d}=d^{(\ell )}$$

实际上就是一层一层的训练，这里有一个疑问为什么不一起训练，是复杂度问题吗？

第二阶段是：

$$\text{ train with backprop on pre-trained NNet to fine-tune all }\left\{w_{ij}^{(\ell )}\right\}$$

当然自编码的实现由正则化规则和不同的结构（ different architectures and regularization schemes）而丰富多样。

降噪自编码器（Denoising Autoencoder）

下面学习一种新的正则化技术。

过拟合的成因一般有三种：数据量过小，噪声过大，算法过于强大。

那么现在提出一种降噪模型，什么意思呢？

将下述形式的样本数据（将原数据和人工噪声混合数据作为输入，将原数据作为输出）输入自编码器中：

$$\begin{array}{c}\left\{\left({\tilde{\mathbf{x}}}_1,{\mathbf{y}}_1={\mathbf{x}}_1\right),\left({\tilde{\mathbf{x}}}_2,{\mathbf{y}}_2={\mathbf{x}}_2\right),\dots ,\left({\tilde{\mathbf{x}}}_N,{\mathbf{y}}_N={\mathbf{x}}_N\right)\right\}\\ \text{ where }{\tilde{\mathbf{x}}}_n={\mathbf{x}}_n+\text{ artificial noise }\end{array}$$

训练出模型：

$$g(\tilde{x})\approx x$$

人工的噪声或者说 hint（例如旋转图像，缩小图像） 常常用于神经网络或者其他模型。

主成分分析（Principal Component Analysis）

线性自编码器假设函数（Linear Autoencoder Hypothesis）

对于一个线性神经网络模型来说，这里则不需要 tanh 函数了，也就是说

$$h_k(\mathbf{x})=\sum _{j=0}^{\tilde{d}}{w}_{jk}^{(2)}\left(\sum _{i=0}^d{w}_{ij}^{(1)}{x}_i\right)$$

现在考虑三个特殊条件：

1. 为了简化，先不考虑 $x_0$，让输入和输出个数一样 ，也就是

$$h_k(\mathbf{x})=\sum _{j=0}^{\tilde{d}}{w}_{jk}^{(2)}\left(\sum _{i=1}^d{w}_{ij}^{(1)}{x}_i\right)$$

2. 假设 $\tilde{d}<d$，以确保非零解（non-trivial solution），因为当 $\tilde{d}>=d$ 可以想象出权重向量是非常稀疏的。

3. 加入前面提及的正则化约束条件 $w_{ij}^{(1)}=w_{ji}^{(2)}=w_{ij}$

$$h_k(\mathbf{x})=\sum _{j=0}^{\tilde{d}}{w}_{kj}\left(\sum _{i=1}^d{w}_{ij}{x}_i\right)$$

同时可以获取权重矩阵 $\mathrm{W}=\left[w_{ij}\right]\text{ of size }d\times \tilde{d}$，那么线性自编码器的假设函数为：

$$\mathbf{h}(\mathbf{x})={\mathrm{W}\mathrm{W}}^T\mathbf{x}$$

线性自编码器的误差函数（Linear Autoencoder Error Function）

可以根据平方误差写出误差函数：

$$E_{\mathrm{i}\mathrm{n}}(\mathbf{h})=E_{\mathrm{i}\mathrm{n}}(\mathrm{W})=\frac{1}{N}\sum _{n=1}^N{\Vert {\mathbf{x}}_n-{\mathrm{W}\mathrm{W}}^T{\mathbf{x}}_n\Vert }^2\text{ with }d\times \tilde{d}\text{ matrix }\mathrm{W}$$

但是这里有一点，需要计算关于 $\mathrm{W}$ 的四次多项式。

这里用到一些线性代数的知识，特征分解（eigen-decompose）：

$${\mathrm{W}\mathrm{W}}^T=\mathrm{V}\Gamma {\mathrm{V}}^T$$

$\mathrm{W}$ 是正规矩阵的充要条件是：存在酉矩阵，使得 $\mathrm{W}$ 酉相似于对角矩阵

其中

1. $\mathrm{V}$ 是 $d\times d$ 的正交（orthogonal）矩阵（又叫酉矩阵），并且 ${\mathrm{V}\mathrm{V}}^T={\mathrm{V}}^T\mathrm{V}={\mathrm{I}}_d$。
2. $\Gamma$ 为对角矩阵，且只有 $\le \tilde{d}$ 个非零项。

${\mathrm{W}\mathrm{W}}^T{\mathbf{x}}_n=\mathrm{V}\Gamma {\mathrm{V}}^T{\mathbf{x}}_n$ 中的各个参数的物理意义：

1. ${\mathrm{V}}^T$ ：将数据 ${\mathbf{x}}_n$ 进行坐标转换（旋转和镜像）。
2. $\Gamma$ ：令上一步获取的矩阵中 $\ge d-\tilde{d}$ 个参数为零，并缩放其他参数。
3. $\mathrm{V}$ ：将上一步获取的数据，根据系数和基向量进行坐标重构（反旋转和反镜像）。

那么根据这个物理意义可以写出如下表示：

$${\mathbf{x}}_n={\mathrm{V}\mathrm{I}\mathrm{V}}^T{\mathbf{x}}_n$$

也就是说只进行旋转和反旋转，并不对参数进行设成零或放缩操作。

那么误差函数最小化问题便转换为了 $\Gamma$ 和 $\mathrm{V}$ 的优化问题。

也就是说：

$$\underset{\mathbf{V}}{\min }\underset{\Gamma }{\min }\frac{1}{N}\sum _{n=1}^N\Vert \underset{{\mathbf{x}}_n}{{\mathrm{VIV}}^T{\mathbf{x}}_n}-\underset{\mathbf{W}{\mathbf{W}}^{\top }{\mathbf{x}}_n}{V\Gamma {\mathbf{V}}^T{\mathbf{x}}_n}{\Vert }^2$$

直观上来说由于 $\mathrm{V}$ 只是做了一个旋转动作，所以并不会影响向量的长度，所以将其拿掉。

$$\underset{\mathbf{V}}{\min }\underset{\Gamma }{\min }\frac{1}{N}\sum _{n=1}^N\Vert \left(I-\Gamma \right){\mathbf{V}}^T{\mathbf{x}}_n{\Vert }^2$$

先不考虑 $\mathrm{V}$，可以改写为：

$$\underset{\Gamma }{\min }\sum \Vert (\mathrm{I}-\Gamma )(\text{ some vector }){\Vert }^2$$

由于 $\mathrm{I}-\Gamma$ 是一个对角矩阵，那么为了满足上述优化问题，那么该对角矩阵应该有尽可能多的零值。由于 $\Gamma$ 中有 $\le \tilde{d}$ 非零值，那么也就是说最多有 $\tilde{d}$ 个 1 使得 $\mathrm{I}-\Gamma$ 零值最多。

那么现在先假设

$$\Gamma =\left[\begin{array}{cc}{\mathrm{I}}_{\tilde{d}}& 0\\ 0& 0\end{array}\right]$$

然后在求取 $\mathrm{V}$ 的值来满足这一条件，那么根据 $\mathrm{I}-\Gamma =\left[\begin{array}{cc}0& 0\\ 0& {\mathbf{I}}_{d-\tilde{d}}\end{array}\right]$ 的最优解将优化问题改为：

$$\underset{\mathbf{V}}{\min }\sum _{n=1}^N{\Vert \left[\begin{array}{cc}0& 0\\ 0& {\mathbf{I}}_{d-\tilde{d}}\end{array}\right]{\mathbf{V}}^T{\mathbf{x}}_n\Vert }^2\equiv \underset{\mathbf{v}}{\max }\sum _{n=1}^N{\Vert \left[\begin{array}{cc}{\mathbf{I}}_{\tilde{\alpha }}& 0\\ 0& 0\end{array}\right]{\mathbf{V}}^T{\mathbf{x}}_n\Vert }^2$$

首先假设 $\tilde{d}=1$，那么只有 ${\mathrm{V}}^T$ 的第一行 ${\mathrm{v}}^T$ 被用到了：

$$\underset{\mathbf{v}}{\max }\sum _{n=1}^N{\mathbf{v}}^T{\mathbf{x}}_n{\mathbf{x}}_n^T\mathbf{v}\text{ subject to }{\mathbf{v}}^T\mathbf{v}=1$$

那么最优解用拉格朗日乘数法可以表示为：

$$\sum _{n=1}^N{\mathbf{x}}_n{\mathbf{x}}_n^T\mathbf{v}=\lambda \mathbf{v}$$

可以看出 $\mathbf{v}$ 是 $X^{T}X$ 的一个特征向量，其中 $X^T=[{\mathbf{x}}_1,\cdots ,{\mathbf{x}}_N]$。那么最优的 $\mathbf{v}$ 应该是最大特征值对应的特征向量。

那么对于任意的 $\tilde{d}$，${\left\{{\mathbf{v}}_j\right\}}_{j=1}^{\tilde{d}}$ 应该是 Top $\tilde{d}$ 特征值对于的特征向量，而 ${\mathbf{w}}_j$ 的组成基本上就是这些特征向量，也就是说：

$$\text{ optimal }\left\{{\mathbf{w}}_j\right\}=\left\{{\mathbf{v}}_j\text{ with }\left[\left[{\gamma }_j=1\right]\right]\right\}=\text{ top eigenvectors }$$

线性自编码器：实际上就是投影到这些与数据 $\left\{{\mathbf{x}}_n\right\}$ 最匹配的几个正交向量。

线性自编码器的本质就是，向这些垂直的向量上做投影后，保证它们的和最大。

$$\text{ maximize }\sum (\text{ maginitude after projection }{)}^2$$

实现流程为：

$$\begin{array}{l}\text{ 1. calculate }\tilde{d}\text{ top eigenvectors }{\mathbf{w}}_1,{\mathbf{w}}_2,\dots ,{\mathbf{w}}_{\tilde{d}}\text{ of }{\mathbf{X}}^T\mathbf{X}\\ \text{ 2. return feature transform }\mathbf{\Phi }(\mathbf{x})=\mathbf{W}(\mathbf{x})\end{array}$$

主成分分析（PCA）的实现与之类似，其本质是做完投影后再这些投影上的变化量（variance）最大，也就是说具有多样性，即找出那些差异性较大的特征，也就是相关性较小的特征将被留下，如果两个特征的相关性较大那么尽可能只留其中一个：

$$\text{ maximize }\sum (\text{ variance after projection })$$

所以 PCA 经常用于降维。

PCA的具体实现流程 ：

$$\begin{array}{l}\text{ 1. let }\overline{\mathbf{x}}=\frac{1}{N}{\sum }_{n=1}^N{\mathbf{x}}_n,\text{ and let }{\mathbf{x}}_n\leftarrow {\mathbf{x}}_n-\overline{\mathbf{x}}\\ \text{ 2. calculate }\tilde{d}\text{ top eigenvectors }{\mathbf{w}}_1,{\mathbf{w}}_2,\dots ,{\mathbf{w}}_{\tilde{d}}\text{ of }{\mathbf{X}}^T\mathbf{X}\\ \text{ 3. return feature transform }\mathbf{\Phi }(\mathbf{x})=\mathbf{W}(\mathbf{x}-\overline{\mathbf{x}})\end{array}$$

特征值和特征向量的意义：图片压缩

以图片压缩为例，比如说，有下面这么一副 $512\times 512$ 的图片（方阵才有特征值，所以找了张正方形的图）：

这个图片可以放到一个矩阵里面去，就是把每个像素的颜色值填入到一个 $512\times 512$ 的 A 矩阵中。

加入该矩阵可以对角化的话，那么可以做如下特征分解（谱分解）：

$$A=P\Lambda P^{-1}$$

其中，$\Lambda$ 是对角阵，对角线上是从大到小排列的特征值。

在 $\Lambda$ 中只保留前面50个的特征值（也就是最大的50个，其实也只占了所有特征值的百分之十），其它的都填0，重新计算矩阵后，恢复为下面这样的图像：

效果还可以，其实一两百个特征值之和可能就占了所有特征值和的百分之九十了，其他的特征值都可以丢弃了。