Single View Metrology 单视图度量衡 复现

（本文作为课程作业记录）

摘 要

本文描述如何通过只给出从图像确定的最小几何信息的单透视图来计算3D仿射量。其中有代表性的最小信息有基准平面的消失线和不平行于此平面的方向消失点。结果表明，即使没有相机校准的知识（例如焦距），也没有相机和环境的明确关系（例如姿势），依然可以从图像中确定仿射场景结构。

具体而言，本文展示如何（1）在带有一个公共的缩放系数下，计算基准面和与之平行的平面的距离；（2）计算基准面和任何与之平行的平面的长度与面积比；（3）确定相机位置。从这些成果中可以引申出一个简单的几何学。

在此基础上，本文用python复现了论文《Single View Metrology》¹中的一些示例结果。

关键词：3D重建；视频测量；摄影测量法

预备知识

在本文中，相机模型是一个中心投影。我们假设在场景中，基准面的消失线可以在图像上测量得出，另一个方向（不平行于此平面）的消失点也是如此。这些信息总体上可以容易地从有结构的场景的图片中获得。例如径向畸变（通常在安保摄像头上使用广角镜头会略微出现）等等会破坏中心投影的影响普遍可以被修复，因此对我们的方法无害。

虽然示意图会展示出相机中心处于一个有限的位置，我们推导的结果仍然对相机中心处于无穷远，或者说图像通过平行投影得出的情况有效。

关于平面的消失线和消失点的基础理论在图1中说明。基准面的消失线$\mathbf{l}$是基准面上的直线的无穷远点在图像上的投影。消失点$\mathbf{v}$是基准方向上无穷远点在图像上的点。要注意到，虽然为了清晰直白，我们通常倾向于将消失点作为"竖直"消失点，这样图像上的消失点就是相机中心在基准面的竖直落脚点，但是基准方向不必是竖直的。同理，基准面通常但不是必须是地平面，这样消失线就是为人熟知的"地平线"。

图 1 基础理论：一个平面与基准面平行，穿过相机中心，平面的消失线$\mathbf{l}$是此平面与图像平面的相交线。消失点$\mathbf{v}$是经过相机中心、与基准方向平行的线和图像平面的相交点。

可以看到，消失线隔开了场景空间的所有点。任何投影在消失线上的点与基准面的距离和相机中心一样高。在其之上则比相机中心距离基准面更远，在其之下则比相机中心距离基准面更近。

理论

2.1 平行平面间的测量

我们希望通过图像上两个点$\mathbf{x}$和${\mathbf{x}}^{\prime }$测量两个平行平面在基准方向上的距离。图
2通过对应点$\mathbf{x}$和${\mathbf{x}}^{\prime }$展示了这个理论。我们用大写字母$\mathbf{X}$表示在空间中的点，小写$\mathbf{x}$表示图像上的点。

定义1.
如果穿过两点$\mathbf{X}$和${\mathbf{X}}^{\prime }$的线与基准方向平行，那么分开平面上（都平行于基准面）的两点$\mathbf{X}$和${\mathbf{X}}^{\prime }$相对应。

图 2 两个平面间的距离与相机中心到两者其中一个平面的距离有关：(a)实际(b)图像。在平面$\pi$上的点$\mathbf{x}$与平面${\pi }^{\prime }$上的点${\mathbf{x}}^{\prime }$对应，一条线上四个对齐的点$\mathbf{x},{\mathbf{x}}^{\prime },\mathbf{v}$与消失线交点$\mathbf{c}$定义了交叉比。交叉比的值确定了平面间实际距离的比值。

因此对应点和消失点共线。例如如果方向是竖直的话，人的头顶和落脚点对应。如果这两点实际距离已知，那么就称为基准距离。

理论1.
给出基准面的消失线和基准方向的消失点，可以计算出带有公共缩放系数的消失线到消失点的距离。这个缩放系数可以通过已知基准长度确定。

证明：在图 2(b)中已标记的四点$\mathbf{x},{\mathbf{x}}^{\prime },\mathbf{c},\mathbf{v}$定义了交叉比。消失点是图像上的场景中的一个无穷远点。鉴于$\mathbf{c}$点在消失线上，$\mathbf{c}$点是一个到平面$\pi$距离$Z_c$的点，其中$Z_c$是相机中心到平面$\pi$的距离。与$Z_c$相关联的交叉比的值确定了穿过$\mathbf{X}$和${\mathbf{X}}^{\prime }$的平面之间的距离$Z$的仿射长度比（或者说${\pi }^{\prime }$取决于交叉比的次序）。要注意到，距离$Z$也可以用线间单应变换来计算，来回避交叉比次序的歧义。

从图 2(b)我们可以得出

$$\frac{d\left(\mathbf{x},\mathbf{c}\right)d\left({\mathbf{x}}^{\prime },\mathbf{v}\right)}{d\left({\mathbf{x}}^{\prime },\mathbf{c}\right)d\left(\mathbf{x},\mathbf{v}\right)}=\frac{d\left(\mathbf{X},\mathbf{C}\right)d\left({\mathbf{X}}^{\prime },\mathbf{V}\right)}{d\left({\mathbf{X}}^{\prime },\mathbf{C}\right)d\left(\mathbf{X},\mathbf{V}\right)}\#(1)$$

其中$d\left({\mathbf{x}}_1,{\mathbf{x}}_2\right)$是俩一般点${\mathbf{x}}_1,{\mathbf{x}}_2$间的距离。鉴于点$\mathbf{v}$
反向投影到无穷远点有$d({\mathbf{X}}^{\prime },\mathbf{V})/d(\mathbf{X},\mathbf{V})=1$，所以（1）中右手边可以归约为$Z_c/(Z_c-Z)$。简单的代数操作即可得出

$$\frac{Z}{Z_c}=1-\frac{d\left(\mathbf{x},\mathbf{c}\right)d\left({\mathbf{x}}^{\prime },\mathbf{v}\right)}{d\left({\mathbf{x}}^{\prime },\mathbf{c}\right)d\left(\mathbf{x},\mathbf{v}\right)}\#(2)$$

一旦相机距离$Z_c$确定，距离$Z$也一并可获得。

然而实践上更常见的是通过另外一种测量方法在图像上获得距离$Z$，也就是基准长度。事实上，给出一个已知基准距离$Z_r$，通过（2）我们可以计算出$Z_c$从而将公式应用到新的一对端点并计算出$Z$。

下面我们推广理论1。

定义2.
如果通过对应点的约束链可以从一个平面集合内一个平面到另一个任意平面，则这个集合内的平面是被链接的。

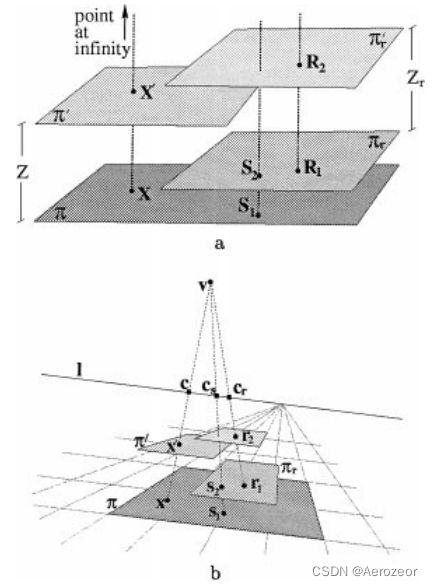
图 3
两个平面间距离与另外两个平面间距离有关系：(a)实际(b)图像。平面$\pi$上的点$\mathbf{x}$对应平面${\pi }^{\prime }$上的点${\mathbf{x}}^{\prime }$。点${\mathbf{s}}_1$对应点${\mathbf{s}}_2$。点${\mathbf{r}}_1$对应点${\mathbf{r}}_2$。${\mathbf{R}}_1$和${\mathbf{R}}_2$的实际距离$Z_r$已知，且作为基准值计算$Z$

理论2.
给出一个被链接的平面集合，任何一对平面间距离足以确定另一对任意平面间的绝对距离。链接的来源是对应点的约束链。

证明： 图3展示了四个平行的平面。注意它们共享了同一条消失线，同时也是多条轴的消失线。它们间距离$Z_r$可以作为基准来计算另外两个的距离$Z$。

• 从四个对齐点$\mathbf{v},{\mathbf{c}}_{\mathbf{r}},{\mathbf{r}}_2,{\mathbf{r}}_1$定义的交叉比和已知点${\mathbf{R}}_1,{\mathbf{R}}_2$距离$Z_r$可以计算出从平面${\pi }_{\mathbf{r}}$到相机间的距离。

• 四个对齐点$\mathbf{v},{\mathbf{c}}_{\mathbf{s}},{\mathbf{s}}_2,{\mathbf{s}}_1$定义的交叉比和相机距离确定了平面${\pi }_{\mathbf{r}}$到$\pi$间距离。相机到平面$\pi$的距离$Z_c$也因此确定。

• 现在可以在（2）中用$Z_c$计算平面$\pi$到${\pi }^{\prime }$间距离$Z$。

2.2 平行平面上的测量

如果基准平面$\pi$经过仿射校准（即已知它消失线），从图像度量值上我们可以计算：

1. 平面上平行线段的长度比
2. 平面上面积之比

另外，消失线被平行于基准面的一束平面共享，于是从束中其他任意平面都可以得出仿射度量值。然而，即使如面积比这样的仿射度量值可以在一个特定的平面得出，但是在不同平面上的区域面积不能直接比较。如果从一个平面到另一个平面平行投影一个区域，由于两个区域都在同一个平面，所以可以得出仿射度量值。平行投影不改变仿射属性。

两个平行平面实际上的映射关系诱导出在图像上两个平面内的点的投影映射关系。这个图像映射是平面同调关系。这个关系是带有五个自由度的投影变换。它具有一条线上的固定点，称为轴，和单独一个不在轴上的固定点，称为顶点。依据反映在图像上的三维空间透视，平面同调关系很自然就可以产生。

在这里，平面消失线和竖直消失点分别是轴和顶点。同调关系可以参数化为

$$H=I+\mu \frac{\mathbf{v}{\mathbf{l}}^{\top }}{\mathbf{v}\cdot \mathbf{l}}\#(3)$$

其中$\mathbf{v}$是消失点，$\mathbf{l}$是平面消失线，$\mu$是缩放系数。$\mathbf{v}$和$\mathbf{l}$确定了四个同调关系自由度。剩下的自由度$\mu$是由任意一对对应点唯一确定。一旦矩阵$H$计算出来，平面上的每个点都可以被转换成对应点，即${\mathbf{x}}^{\prime }=H\mathbf{x}$。

因此我们可以比较两个分开平面上的度量值。尤其是可以计算：

1. 平行线各在自己的平面上的长度之间的比。
2. 各在自己平面上的面积之比

事实上我们可以用同调关系从一个平面上转换所有点到基准平面上。然后从已知的基准面消失线得出仿射度量值。

2.3 确定相机位置

在2.1节中我们依据相机到基准面的距离计算出平面间距离比。反其道行之，我们可以从一个特定已知平面的单独的基准距离$Z_r$计算出相机距离$Z_c$。再者，考虑图1，相机位置对于基准面似乎是竖直消失点对于基准面的反投影。这个反投影已经被从图像到基准面的单应投影完成了（反之亦然）。即使实际场景的坐标框架选择有点随意，框架一固定，单应关系以及相机位置就立刻被定义。

代数形式表示

前面的章节描述基于交叉比计算度量值。在这一节我们延伸出一个独特的代数方法。这对构建几何有几个好处。第一是它回避了交叉比次序的潜在问题。第二是它可以让我们处理极小值和普遍的过度约束设置。第三我们在一个表示形式上整合了不同类型的度量值。第四可以进行不确定性分析。

首先我们在空间内定义一个仿射坐标系$XYZ$。让原点位于基准面内，并在平面上生成$X$和$Y$轴。$Z$轴是基准方向。图像坐标系就是通常的$xy$仿射图像框架。空间上的一个点$\mathbf{X}$通过一个$3\times 4$的投影矩阵$P$投影到图像点$\mathbf{x}$:

$$\mathbf{x}=P\mathbf{X}=\left[\begin{array}{cccc}{\mathbf{p}}_1& {\mathbf{p}}_2& {\mathbf{p}}_3& {\mathbf{p}}_4\end{array}\right]\mathbf{X}$$

其中$\mathbf{x}$和$\mathbf{X}$是形如$\mathbf{x}=(x,y,w{)}^{\top },\mathbf{X}=(X,Y,Z,W{)}^{\top }$的齐次向量。"$=$"意思是带一个缩放系数下相等。

如果我们用消失点来分别指示出$X,Y,Z$方向${\mathbf{v}}_X,{\mathbf{v}}_Y,\mathbf{v}$，显然可以检验$P$的前三列是消失点：${\mathbf{v}}_X={\mathbf{p}}_1,{\mathbf{v}}_Y={\mathbf{p}}_2,\mathbf{v}={\mathbf{p}}_3$，最后一列则是实际空间坐标系原点$\mathbf{o}={\mathbf{p}}_4$。由于我们选择的坐标框架在基准面上的$X,Y$轴${\mathbf{p}}_1={\mathbf{v}}_X,{\mathbf{p}}_2={\mathbf{v}}_Y$是在消失线上的两个单独的点，选择这些点会固定$X,Y$轴，我们将消失线表示为$\mathbf{l}$，为了强调${\mathbf{v}}_X,{\mathbf{v}}_Y$在消失线上，我们将它们表示为${\mathbf{l}}_1^{\perp },{\mathbf{l}}_2^{\perp }$，并且${\mathbf{l}}_i^{\perp }\cdot \mathbf{l}=0$。

投影矩阵的1，2，4列是基准面到图像的单应矩阵的三列。单应矩阵必须要秩为3，不然从基准面到图像的映射会退化。另外，最后一列（坐标原点）不能在消失线上，不然三点共线，列之间不再线性无关。于是我们将其设为${\mathbf{p}}_4=l/\Vert l\Vert =\overline{\mathbf{l}}$。

因此投影矩阵$P$的参数化形式为

$$\begin{array}{c}P=\left[\begin{array}{cccc}{\mathbf{l}}_1^{\perp }& {\mathbf{l}}_2^{\perp }& \alpha \mathbf{v}& \overline{\mathbf{l}}\end{array}\right]\#(4)\end{array}$$

其中$\alpha$是缩放系数。

要注意到竖直消失点$\mathbf{v}$对矩阵P附加了两个约束、$\mathbf{l}$有两个、$\alpha$有一个，总共五个约束。（目前前两列不完全已知，唯一约束仅仅只是垂直于$\mathbf{l}$）。然而一般而言$P$矩阵有十一个自由度，可以认为包括从基准面诱导的从实际场景到图像的单应矩阵的八个、消失点的两个、仿射参数$\alpha$的一个自由度。这里消失线确定了单应矩阵的八个自由度中的两个。

3.1 平行平面间的测量

3.1.1平面到基准面$\pi$的距离

我们希望通过场景中$\mathbf{X}$和$\mathbf{X}{}^{\prime }$测量两个平面的距离。两个点可以选择为$\mathbf{X}=(X,Y,0{)}^{\top },{\mathbf{X}}^{\prime }=(X,Y,Z{)}^{\top }$，它们的映射是$\mathbf{x}$和${\mathbf{x}}^{\prime }$。如果$P$是投影矩阵，那么图像坐标为

$$\mathbf{x}=P\left(\begin{array}{c}X\\ Y\\ 0\\ 1\end{array}\right),{\mathbf{x}}^{\prime }=P\left(\begin{array}{c}X\\ Y\\ Z\\ 1\end{array}\right)$$

上面的等式可以写成

$$\begin{gathered} \mathbf{x}=\rho \left(X{\mathbf{p}}_1+Y{\mathbf{p}}_2+{\mathbf{p}}_4\right)\#(5) \\ {\mathbf{x}}^{\prime }={\rho }^{\prime }\left(X{\mathbf{p}}_1+Y{\mathbf{p}}_2+Z{\mathbf{p}}_3+{\mathbf{p}}_4\right)\#(6) \end{gathered}$$

其中$\rho$和${\rho }^{\prime }$是未知放缩系数。${\mathbf{p}}_i$是矩阵$P$的第$i$列。

由于${\mathbf{p}}_1\cdot \overline{\mathbf{l}}={\mathbf{p}}_2\cdot \overline{\mathbf{l}}=0$，${\mathbf{p}}_4\cdot \overline{\mathbf{l}}=1$，用$\overline{\mathbf{l}}$点乘（5）得到$\rho =\overline{\mathbf{l}}\cdot \mathbf{x}$，于是（6）可以写成

$${\mathbf{x}}^{\prime }={\rho }^{\prime }\left(\frac{\mathbf{x}}{\rho }+\alpha Z\mathbf{v}\right)\#(7)$$

用$\mathbf{x}{}^{\prime }$向量乘（7）中每一项得到

$$\mathbf{x}\times {\mathbf{x}}^{\prime }=-\alpha Z\rho \left(\mathbf{v}\times {\mathbf{x}}^{\prime }\right)\#(8)$$

最后，（8）两边取绝对值得到

$$\alpha Z=-\frac{\Vert \mathbf{x}\times {\mathbf{x}}^{\prime }\Vert }{\left(\overline{\mathbf{l}}\cdot \mathbf{x}\right)\Vert \mathbf{v}\times {\mathbf{x}}^{\prime }\Vert }\#\left(9\right)$$

由于$\alpha Z$是$\alpha$的线性放缩，仿射结构已经得出了。如果$\alpha$已知，$Z$的度量值也可以立刻计算出：

$$Z=-\frac{\Vert \mathbf{x}\times {\mathbf{x}}^{\prime }\Vert }{\left({\mathbf{p}}_4\cdot \mathbf{x}\right)\Vert {\mathbf{p}}_3\times {\mathbf{x}}^{\prime }\Vert }\#\left(10\right)$$

反过来，如果$Z$已知（例如它是一个基准距离），（9）也提供计算$\alpha$的一个方法，并因此移除了仿射歧义。

从多基准值进行度量校准
如果不只一个基准距离已知，$\alpha$的估计值可以由一个误差最小化算法衍生。这里展示当从基准面出发的距离都被测量的情况并最小化代数误差。

对于第$i$个以点${\mathbf{r}}_i,{\mathbf{r}}_{i^{\prime }}$为端点基准距离$Z_i$，我们定义${\beta }_i=\Vert {\mathbf{r}}_i\times {\mathbf{r}}_{i^{\prime }}\Vert ,{\rho }_i=\overline{\mathbf{l}}\cdot {\mathbf{r}}_i,{\gamma }_i=\Vert \mathbf{v}\times {\mathbf{r}}_{{\mathbf{i}}^{\prime }}\Vert$，于是从（9）我们得到

$$\alpha Z{\rho }_i{\gamma }_i=-{\beta }_i\#(11)$$

现在定义$n\times 2$矩阵$A$（对（11）重新组织得）

$$A=\left(\begin{array}{cc}{Z}_1{\rho }_1{\gamma }_1& {\beta }_1\\ ⋮& ⋮\\ Z_i{\rho }_i{\gamma }_i& {\beta }_i\\ ⋮& ⋮\\ Z_n{\rho }_n{\gamma }_n& {\beta }_n\end{array}\right)$$

其中$n$是基准距离的数量。如果没有测量误差，或者$n=1$则有$A\mathbf{s}=0$，其中$\mathbf{s}={\left(s_1{s}_2\right)}^{\top }$是一个齐次2维向量，且

$$\alpha =\frac{s_1}{s_2}\#(12)$$

通常情况下$n>1$，且基准距离都有不确定性，在此情况下，我们找寻令$\Vert A\mathbf{s}\Vert$取最小值的解。那就是对应$2\times 2$的矩阵$M=A^{\top }A$的最小特征值的特征向量。此时$\alpha$仍然可以通过（12）计算。

3.1.2两个平行平面间的距离

投影矩阵$P$只定义在基准面上。在这一节我们根据平行平面${\pi }^{\prime }$确定投影矩阵$P^{\prime }$，以及如何计算到平面${\pi }^{\prime }$的距离。

图 4 度量平行于基准面$\pi$的任意两个平面${\pi }^{\prime },{\pi }^{\prime \prime }$间的距离

假设实际坐标通过基准方向上的$Z_r$从平面$\pi$变换到${\pi }^{\prime }$（图 4），我们可以参数化新投影矩阵$P^{\prime }$为

$$P^{\prime }=\left[\begin{array}{cccc}{\mathbf{p}}_1& {\mathbf{p}}_2& {\mathbf{p}}_3& Z_r{\mathbf{p}}_3+{\mathbf{p}}_4\end{array}\right]\#(13)$$

${\pi }^{\prime },\pi {}^{\prime \prime }$间的距离$Z^{\prime }$可以计算

$$Z^{\prime }=-\frac{\Vert {\mathbf{x}}^{\prime }\times {\mathbf{x}}^{\prime \prime }\Vert }{{\rho }^{\prime }\Vert {\mathbf{p}}_3\times {\mathbf{x}}^{{}^{\prime \prime }}\Vert }\#\left(14\right)$$

其中

$${\rho }^{\prime }=\frac{{\mathbf{x}}^{\prime }\cdot {\mathbf{p}}_4}{1+Z_r{\mathbf{p}}_3\cdot {\mathbf{p}}_4}$$

3.2 平行平面上的测量

正如在2.2节所描述的，给出平面$\pi$到${\pi }^{\prime }$同调矩阵我们就可以让一个平面上的所有点转换到另一个平面，从而在另一个平面上得出仿射度量值。同调矩阵可以直接从投影矩阵中得出。平面到图像的单应矩阵就是忽略第三列的投影矩阵

$$H=\left[\begin{array}{ccc}{\mathbf{p}}_1& {\mathbf{p}}_2& {\mathbf{p}}_4\end{array}\right],H^{\prime }=\left[\begin{array}{ccc}{\mathbf{p}}_1& {\mathbf{p}}_2& Z_r{\mathbf{p}}_3+{\mathbf{p}}_4\end{array}\right]$$

于是$H=H^{\prime }{H}^{-1}$是图像上在平面$\pi$的点到${\pi }^{\prime }$的映射，而且定义了同调矩阵。通过检验，由于${\mathbf{p}}_1\cdot {\mathbf{p}}_4={\mathbf{p}}_2\cdot {\mathbf{p}}_4=0$，所以$\left(I+Z_r{\mathbf{p}}_3{\mathbf{p}}_4^{\top }\right)H=H^{\prime }$，于是同调矩阵：

$$H=I{+Z}_r{\mathbf{p}}_3{\mathbf{p}}_4^{\top }\#\left(15\right)$$

另一方面，从（4）同调矩阵可写为

$$H=I+\psi \mathbf{v}{\overline{\mathbf{l}}}^{\top }\#\left(16\right)$$

其中$\mathbf{v}$是竖直消失点，$\overline{\mathbf{l}}$是平面消失线的正则化，$\psi =\alpha Z_r$（参考（3））。

如果$Z_r$且矩阵$P$后两列已知，同调矩阵就可以用（15）计算，如果只有$\mathbf{v}$，$\overline{\mathbf{l}}$已知，对应点$\mathbf{r},{\mathbf{r}}^{\prime }$可见，那么同调参数$\psi$可以用（9）计算（因为$\alpha Z_r=\psi$）而不需要知道$\alpha ,Z_r$的值。

3.3 确定相机位置

假设相机中心是$\mathbf{C}={\left(X_c,Y_c,Z_c.W_c\right)}^{\top }$,于是由于$P\mathbf{C}=0$，有

$$P\mathbf{C}={\mathbf{p}}_1{X}_c+{\mathbf{p}}_2{Y}_c+{\mathbf{p}}_3{Z}_c+{\mathbf{p}}_4{W}_c=0\#\left(17\right)$$

给出问题的解答（通过克莱姆法则）

$$\begin{array}{ccc}{X}_c& =& -\det \left[\begin{array}{ccc}{\mathbf{p}}_2& {\mathbf{p}}_3& {\mathbf{p}}_4\end{array}\right]\\ Y_c& =& \det \left[\begin{array}{ccc}{\mathbf{p}}_1& {\mathbf{p}}_3& {\mathbf{p}}_4\end{array}\right]\\ Z_c& =& -\det \left[\begin{array}{ccc}{\mathbf{p}}_1& {\mathbf{p}}_2& {\mathbf{p}}_4\end{array}\right]\\ W_c& =& \det \left[\begin{array}{ccc}{\mathbf{p}}_1& {\mathbf{p}}_2& {\mathbf{p}}_3\end{array}\right]\end{array}\#(18)$$

于是相机中心也被定义了。如果$\alpha$未知，我们可以

$$\begin{array}{ccc}{X}_c& =& -\det \left[\begin{array}{ccc}{\mathbf{p}}_2& \mathbf{v}& {\mathbf{p}}_4\end{array}\right]\\ Y_c& =& \det \left[\begin{array}{ccc}{\mathbf{p}}_1& \mathbf{v}& {\mathbf{p}}_4\end{array}\right]\\ \alpha Z_c& =& -\det \left[\begin{array}{ccc}{\mathbf{p}}_1& {\mathbf{p}}_2& {\mathbf{p}}_4\end{array}\right]\\ W_c& =& \det \left[\begin{array}{ccc}{\mathbf{p}}_1& {\mathbf{p}}_2& \mathbf{v}\end{array}\right]\end{array}\#(19)$$

来获得带有一个仿射放缩系数$\alpha$的距离$Z_c$。如果是以前，我们需要利用$\alpha$的知识来更新$Z_c$，或者需要相机高度的知识来计算$\alpha$，从而更新仿射框架。

可以注意到，仿射观察条件（相机中心在无穷远点）在（18）（19）上没有问题。因为其实我们可以让$\overline{\mathbf{l}}={\left[\begin{array}{ccc}0& 0& \ast \end{array}\right]}^{\top },\mathbf{v}={\left[\begin{array}{ccc}\ast & \ast & 0\end{array}\right]}^{\top }$。由于
$W_c=0$，我们此时获得在平面无穷远点的相机中心。在${\pi }_{\infty }$的点代表平行投影的观察方向。

如果观察点是有限的（即不是仿射观察条件），$\alpha Z_c$的公式可以更进一步，通过两边标量乘$\overline{\mathbf{l}}$可以得到

$$\alpha Z_c=-\frac{1}{\overline{\mathbf{l}}\cdot \mathbf{v}}\#(20)$$

代码复现

在这一节中我们复现了论文《Single View Metrology》中的一些示例结果。

图 5展示了怎么在额外给出一个垂直基准距离下计算人的升高。图 6展示了如何测量水平线到地面的高度。图 6的流程如下：

• 通过相交的（场景中）竖直边缘计算竖直消失点$\mathbf{v}$。

所有与地面平行的线都交于地平线上的点，则

• 通过右边木板的边缘计算地平线上的交点${\mathbf{v}}_1$。
• 通过左边的木板和房顶计算另一个交点${\mathbf{v}}_2$。
• 通过两个点算出平面消失线$\mathbf{l}$($\mathbf{l}={\mathbf{v}}_1\times {\mathbf{v}}_2$)。
• 通过基准距离用（9）算出$\alpha$。
• 选择${\mathbf{l}}_{x^{\prime }}$上的任意两点来构造平行线${\mathbf{l}}_{x^{\prime }}$。
• 可以算出与之有关的消失点${\mathbf{v}}_h({\mathbf{v}}_h={\mathbf{l}}_{x^{\prime }}\times \mathbf{l})$。
• 与${\mathbf{l}}_{x^{\prime }}$平行的直线${\mathbf{l}}_x$必须经过点${\mathbf{v}}_h$，再另外选择一个点就可以确定${\mathbf{l}}_x$。
• 从${\mathbf{l}}_{x^{\prime }}$中选择一点${\mathbf{x}}^{\prime }$，可以计算在${\mathbf{l}}_x$上与之对应的点$\mathbf{x}=\left({\mathbf{x}}^{\prime }\times \mathbf{v}\right)\times {\mathbf{l}}_x$。
• 用（10）可以算出两点间距离$Z$

图 5
从单视图中测量人的身高：(a)原图(b)示例($c$)复现结果。在示例中消失线以白色线表示，基准距离是右边的窗框高度。在复现结果中用于确定消失点${\mathbf{v}}_x,{\mathbf{v}}_y,\mathbf{v}$的平行线以蓝色线表示。消失线以红色线表示。基准距离是柱高度201cm以紫色线表示。身高以黄色线表示，结果为178.08cm。

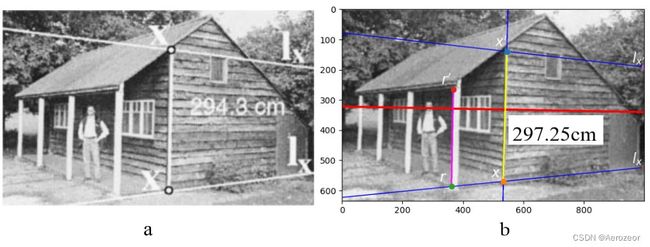
图 6
利用平行线计算高度：(a)示例(b)复现结果。在上方的蓝色线是${\mathbf{l}}_{x^{\prime }}$，在下方的是${\mathbf{l}}_x$。竖直的蓝色线经过竖直消失点。$\mathbf{x},{\mathbf{x}}^{\prime }$是一对对应点，分别与窗上边缘和地面在同一平面，计算结果297.25cm。

在这步骤中计算$\alpha$的代码如下

def cal_alpha(Z: list, r1: list, r2: list, v, l):
    alpha=0
    beta_i = rou_i = gamma_i = 0
    A = np.zeros([len(Z), 2])
    for i in range(len(Z)):
        beta_i = np.linalg.norm(np.cross(r1[i], r2[i]))
        l_bar = l / np.linalg.norm(l) #l的正则化
        rho_i = np.dot(l_bar, r1[i])
        gamma_i = np.linalg.norm(np.cross(v, r2[i]))
        A[i, 0] = Z[i] * rho_i * gamma_i
        A[i, 1] = beta_i

    if len(Z) == 1:#只有一个基准距离
        alpha = (-1.0 * beta_i) / (Z[0] * rho_i * gamma_i)
    else:
        M = np.dot(A.T, A)
        lam,xi = np.linalg.eig(M)#计算特征值和向量
        s = xi[:,np.argmin(lam)]#取最小特征值的特征向量
        alpha = s[0] / s[1]
    return alpha

计算距离Z的代码为

'''
其他代码中已定义以下内容
P = np.zeros([3, 4])
p1 = P[:, 0]
p2 = P[:, 1]
p3 = P[:, 2]
p4 = P[:, 3]
'''
def cal_z(point1, point2):
    return -np.linalg.norm(np.cross(point1, point2)) / (np.dot(p4, point1) * np.linalg.norm(np.cross(p3, point2)))

图 7反映了如何利用同调关系来计算一个点在平行平面上的对应点。图 8展示了如何在平行平面间比较线段长度。图 9展示如何在平行平面间比较面积大小。计算同调矩阵需要先计算参数$\psi$。$\psi$可以通过（9）计算。需要注意的是，由于python的OpenCV库默认图像坐标系左上角为原点，y轴正方向向下，与示例中设置的图像坐标系不同。所以$\psi$的符号也要变动。在最后，由于矩阵$P$需要带系数$\rho$才能使等式$\mathbf{x}=P\mathbf{X}$成立，所以由$P$推导出的同调矩阵$H$也需要带缩放系数。

图 7
从平面到另一个平行平面的点的同调映射：(a)原图，柜子的上顶面和下底面是平行平面。(b)示例图，共同的消失线（同调轴，上方白色）©示例图，显示物体轮廓(d)复现结果，用于确定消失点${\mathbf{v}}_x,{\mathbf{v}}_y,\mathbf{v}$的平行线以蓝色线表示。消失线以红色线表示。利用相同消失点和消失线推导的同调关系，给出上方选取点$\mathbf{x}$，就能计算出下方对应点${\mathbf{x}}^{\prime }$。橙色线表现了这个关系。

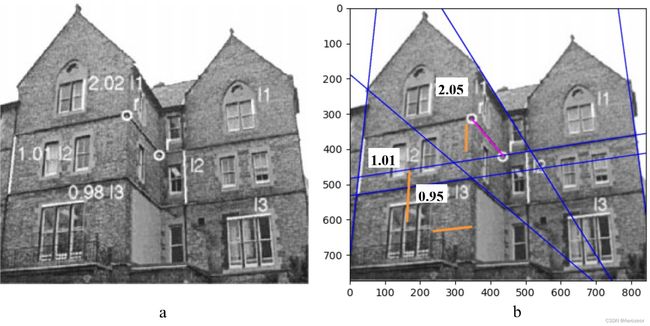
图 8
在两个平面之间测量平行线段长度之比：(a)原图示例(b)复现结果。点$\mathbf{r},{\mathbf{r}}^{\prime }$与消失点、消失线定义了两面墙的同调关系，蓝色线是定义消失点和消失线的平行线。紫色线段是以$\mathbf{r},{\mathbf{r}}^{\prime }$为端点的线段。橙色线是左外墙的线段映射到右外墙的结果。

图 9
测量在两个不同平面上的面积之比：(a)原图，目标是测量两个窗户的面积(b)复现效果图。橙色框是A1映射到A2平面的结果。利用$\mathbf{r},{\mathbf{r}}^{\prime }$计算同调关系，并转换A1点到A2所在平面上，获得两个窗户的面积比为$A1/A2=1.2$

下面是计算$\psi ,H$、同调对应点、以及额外缩放系数$\rho$的代码

def cal_psi(point1, point2, v, l):
    l_bar = l / np.linalg.norm(l)
    # 使用公式（9）计算psi。没有负号是因为图像坐标系y轴与示例中y轴正方向相反
    return np.linalg.norm(np.cross(point1, point2)) / ((np.dot(l_bar, point1)) * (np.linalg.norm(np.cross(v, point2))))

def cal_H_tilde(psi, v, l):
    l_bar = l / np.linalg.norm(l)
    return np.identity(3) + psi * (np.dot(np.mat(v).T, np.mat(l_bar)))

def correspond(H_tilde, point):
    correspond_point = np.dot(H_tilde, point)
    correspond_point = np.array(correspond_point)[0]  # 由矩阵转为向量
    correspond_point = correspond_point / correspond_point[-1]
    return correspond_point # 返回结果之后还需要乘缩放系数rho_tilde

rho_tilde = np.linalg.norm(reference_bottom_point) / np.linalg.norm(correspond(reference_top_point))

图 10展示了如何计算在不同平行平面上物体的高度。地平面是基准面$\pi$，将桌子桌面作为平面${\pi }^{\prime }$。用（14）即可以算出高度。

下面是计算文件夹高度$Z^{\prime }$的代码

'''
其他代码中已定义以下内容
P = np.zeros([3, 4])
p1 = P[:, 0]
p2 = P[:, 1]
p3 = P[:, 2]
p4 = P[:, 3]
'''
def cal_z_prime(point2, point3):
    rho_prime = np.dot(point2, p4) / (1 + reference_distance * np.dot(p3, p4))
    return -np.linalg.norm(np.cross(point2, point3)) / (rho_prime * (np.linalg.norm(np.cross(p3, point3))))

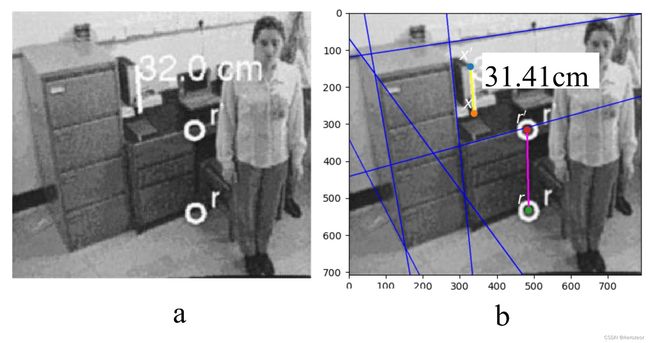
图 10
在不同平面上计算物体高度：(a)原示例结果(b)复现结果。蓝色线是定义消失点和消失线的平行线。紫色线是基准距离，桌子$\mathbf{r},{\mathbf{r}}^{\prime }$的高度设定为60cm，计算出文件夹高度31.41cm。

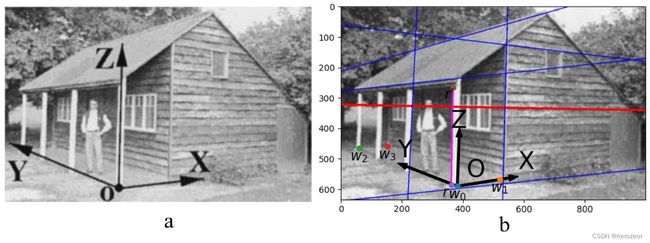
图 11
计算相机位置：(a)原示例图(b)附带标识了参考点的复现图。$w_i$表示用于计算单应矩阵的走廊矩形四个点。$w_0$与原点重合。紫色线是基准距离。坐标系表示将空间坐标系$XYZ$按照图示构造。设定走廊矩形长宽为$830cm\times 120cm$。计算出相机位置为$X_c=-385.36cm,Y_c=-651.01cm,Z_c=161.29cm$

图11展示在确定空间坐标系时，如何计算相机位置。在这里，空间坐标原点不再被设定为${\mathbf{p}}_4=\overline{\mathbf{l}}$，而是${\mathbf{p}}_4=w_0$。这导致两个结果。一是需要修改$\alpha$的计算方法，因为之前计算方法依赖于${\mathbf{p}}_4=\overline{\mathbf{l}}$，$\overline{\mathbf{l}}\cdot {\mathbf{p}}_4=1$。二是需要另一种方法计算从实际到图像的单应矩阵$H$，因为矩阵$P$现在是未知的。计算单应矩阵$H$可以利用图像点和空间坐标的点的关系联立方程用矩阵解法。（至少4对点，8个方程）。²

def cal_H(world_point:list,img_point:list):
    A = np.zeros([2 * len(img_point), 9])
    for i in range(len(img_point)):
        ip = img_point[i]
        wp = world_point[i]
        A[i * 2] = [wp[0], wp[1], 1, 0, 0, 0, -wp[0] * ip[0], -wp[1] * ip[0], -ip[0]]
        A[i * 2 + 1] = [0, 0, 0, wp[0], wp[1], 1, -wp[0] * ip[1], -wp[1] * ip[1], -ip[1]]

    lam, xi = np.linalg.eig(np.dot(A.T, A))
    H_vector = xi[:, np.argmin(lam)]
    return np.array([H_vector[:3], H_vector[3:6], H_vector[6:9]])

由于前提发生变换$(\overline{\mathbf{l}}\cdot {\mathbf{p}}_4\ne 1)$，所以$\alpha$的计算方法也发生了变化

def cal_alpha2(z: list, r1: list, r2: list, v, l):
    global alpha
    beta_i = rho_i = gamma_i = 0
    A = np.zeros([len(z), 2])
    for i in range(len(z)):
        beta_i = np.linalg.norm(np.cross(r1[i], r2[i]))
        l_bar = l / np.linalg.norm(l)
        # 这里更改了代码，因为np.dot(l_bar,p4)不等于1
        rho_i = np.dot(l_bar, r1[i]) / (np.dot(l_bar, p4))

        gamma_i = np.linalg.norm(np.cross(v, r2[i]))
        A[i, 0] = z[i] * rou_i * gamma_i
        A[i, 1] = beta_i

    if len(z) == 1:
        alpha = (-1.0 * beta_i) / (z[0] * rho_i * gamma_i)
    else:
        M = np.dot(A.T, A)
        lam, xi = np.linalg.eig(M)  # 计算特征值和向量
        s = xi[:, np.argmin(lam)]  # 取最小特征值的特征向量
        alpha = s[0] / s[1]

在算出单应矩阵后就可以得到投影矩阵$P$的1，2，4列。以下是获得矩阵$P$的流程。

    p1[:] = H[:, 0]
    p2[:] = H[:, 1]
    p4[:] = H[:, 2]
    #cal_alpha2()函数需要p4。所以需要计算p4后才运行cal_alpha2()
    alpha=cal_alpha2(reference_distances, reference_ground_points, reference_plane_points, v, l)
    p3[:] = alpha * v[:]

算出矩阵$P$后依据（18）算出相机位置（前面提到，由于坐标朝向问题，$Z_c$符号实际上是相反的。）

Xc = -np.linalg.det(np.array([p2, p3, p4]).T)
Yc = np.linalg.det(np.array([p1, p3, p4]).T)
Zc = -np.linalg.det(np.array([p1, p2, p4]).T)
Wc = np.linalg.det(np.array([p1, p2, p3]).T)

参考文献

---

1. A. Criminisi, I. Reid, and A. Zisserman, “Single view metrology,”
   International Journal of Computer Vision, vol. 40, no. 2, pp.
   123–148, 2000. ↩︎

2. A. Criminisi, I. Reid, and A. Zisserman, “A plane measuring
   device,” Image and Vision Computing, vol. 17, no. 8, pp. 625–634,1999. ↩︎