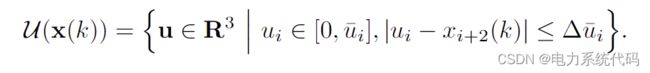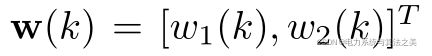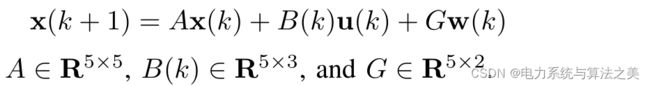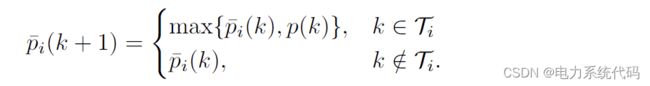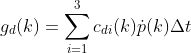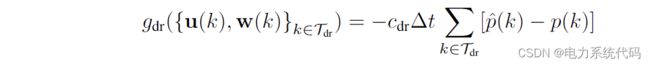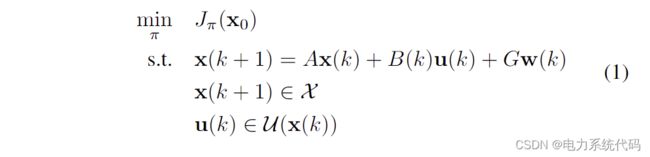需求响应|动态冰蓄冷系统与需求响应策略的优化研究（Matlab代码实现）
欢迎来到本博客❤️❤️❤️
作者研究：主要研究方向是电力系统和智能算法、机器学习和深度学习。目前熟悉python网页爬虫、机器学习、群智能算法、深度学习的相关内容。希望将计算机和电网有效结合！⭐️⭐️⭐️
目前更新：电力系统相关知识，期刊论文，算法，机器学习和人工智能学习。
支持：如果觉得博主的文章还不错或者您用得到的话，可以关注一下博主，如果三连收藏支持就更好啦！这就是给予我最大的支持！
欢迎您的到来
⛅⛅⛅ 个人主页：科研室
所有代码目录：电气工程科研社
【现在公众号名字改为：荔枝科研社】
本文目录如下：⛳️⛳️⛳️
目录
1 概述
2 控制算法讲解
2.1 随机开环最优控制 (OLOC)
2.2 模型预测控制(MPC)
3 数学模型建立
3.1 物理模型
3.2 经济模型
3.3 随机最优控制问题
4 算例及运行结果
5 Matlab代码实现
6 写在最后
1 概述
在现阶段全球气温升高的背景下，我觉得这个课题很值得研究。由于二氧化碳的大量排放，全球变暖。
(1)所有新型电力系统的提出思维独到，大力发展风、光等新能源尤为重要，所以我写了很多微电网的文章代码。搜索方法如下。
（2）需求响应主要分为基于价格和基于激励的需求响应。以往电力系统调度主要靠发电侧，借鉴了漂亮国，国家也开始重视需求响应。需求响应计划鼓励消费者在电网高峰时削减负荷。我也写了很多关于需求响应的文章代码。
(3)本文的创新点：具有冰蓄冷系的建筑物主要使用它来转移冷负荷。当电价低时生产冰或冷冻水，并在电价高时储存以给用户提供冷能。本文用随机最优控制和模型预测控制 (MPC) 结合求解。
2 控制算法讲解
本文使用了两种算法： 随机开环最优控制 (SOOC) 和模型预测控制 (MPC) 。
2.1 随机开环最优控制 (OLOC)
对于扰动随机的随机最优控制问题，本文采用文献[8]中的随机最优开环控制方法(SOOC)解决。下面重点讲解模型预测控制（MPC）。
2.2 模型预测控制(MPC)
2.2.1 概述
MPC 最早起源于石油化工等工业界，旨在解决经典的比例-积分-微分（PID）控制难以处理多变量约束优化控制的问题。作为一种基于模型的控制算法，其滚动优化问题中的系统模型可以是描述系统动态行为的任意形式的模型，因此从原理上该方法可处理时变或非时变、线性或非线性、有时滞或无时滞的系统约束最优控制问题。正是基于该特点，MPC 作为一类适用性非常强的控制算法在电力系统优化控制领域得到了广泛的应用。
随着 MPC 理论日趋成熟，国内外很多企业专门研发了商业化MPC 软件包。
模 型 预 测 控 制（model predictive control，MPC）是 近 年 来 最 引 人 关 注 的 一 类 反 馈 控 制 策略，主要由模型预测、滚动优化和反馈校正 3 个环节构成。
2.2.2 作用机理
MPC 从 20 世纪七八十年代开始萌芽，经历了模型算法控制、动态矩阵控制、广义预测控制 3 个阶段的过渡，已经发展为成熟的控制理论［21］，其原理如图 1 所示，求解步骤为：在每一个采样时刻，根据当前测量信息，在线求解一个有限时域开环优化问题，并将得到的控制序列的第 1 个元素作用于被控对象。在下一个采样时刻，重复上述过程，用新的测量值重构优化问题并重新求解［22］，可以得出如下结论。
1）与常规最优控制方法不同，MPC 的优化目标并非全局不变，而是采用滚动向前式的有限时域优化目标，以局部最优解逐级逼近全局最优解。这种有限时域优化策略可兼顾模型失配、时变等不确定性，是最优控制和不确定性情况下的折中。
2）MPC 将控制问题转化为有限时域的滚动式开环优化问题，能考虑被控对象的未来行为特征，易于处理多耦合系统，故可结合各种优化求解算法而易于拓展。
图1 MPC原理
3 数学模型建立
本文详细对成本进行建模。物理模型是建立在文献[6]中提出的物理模型的基础上，扩展到包括第二台制冰机、考虑制冰机的爬坡约束、时变性能系数以及非理想的存储和热交换器效率。得到的模型是一个具有线性时变动力学的完全观测MIMO随机系统。
在后文中，变量k对集合进行了索引
={0, . . . , N− 1},N = / Δt为控制视界T中长度Δt (小时)的离散时间步数（本文算例中Δt=0.5）。在本文中，我们取T = 24小时，虽然稍作修改，视界可以延长到一个月或一个冷却季.
3.1 物理模型
3.1.1 系统的状态变量
:冰库的充电状态
,上界为
（本文算例中冰罐容量
为1760
:为建筑冷却不足(kWhth）即前阶段所有未满足的冷却负荷的总和（滞后冷却负荷）。请注意，可能为负数，例如，如果建筑物在一夜之间预冷。
3.1.2 系统的控制变量
:分配给制冰的电功率。（KW）
（本文最大制冰机功率
,最大制冰机斜坡
)
:融化冰所满足的冷负荷。
(本文每个阶段的最大融冰量
，最大融冰爬坡
)
:主冰水机组消耗的功率（KW) ，为主冷水机组（主冷却器）消耗的功率 (kW)
(本文最大主制冰机功率为
，最大主制冰机爬坡
)
对于每个 
，i ∈{1,2,3}，定义最大工作点
和最大斜坡 
。
为了强制执行斜坡约束，我们将 u(k-1) 附加到状态，定义![x(k) = [x1(k),x2(k),u(k -1)^{T}]^{T}](http://img.e-com-net.com/image/info8/71826ddd200948a4bd12142a15bbe0c7.gif){kind=small}
。
这给出了状态约束 x(k) ∈ X =![[0, \overline{x_{1}}]](http://img.e-com-net.com/image/info8/320562307389409aa1539f03f87d6867.gif){kind=small}
×R4 和控制约束 u(k) ∈U(x(k))，其中:
3.1.3 系统的扰动变量
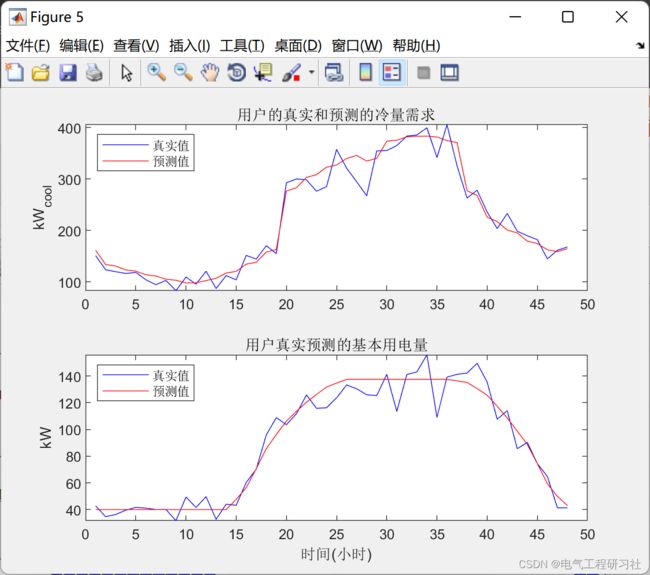
w1(k)为建筑物对冰需求( kWth )
w2 ( k )为建筑物的剩余电气需求( kW )：照明、插头负载等。（也可以理解为建筑物的固定荷载）
我们假设扰动
是服从正态分布的。
我们还假设,对于所有 k ∈T,建筑运营商在
和
的第0阶段都有准确的知识。给定这些定义，状态就按照这个下式演化：
或者更简洁书写为：
其中，β∈[ 0,1 ]为冰滞留率，η∈[ 0,1 ]为水箱与建筑物的换热效率，
和
分别为制冷机组和主制冷机组的性能系数。时间依赖性允许冷水机组性能系数随室外温度变化。
我们假设控制器在第k阶段完全了解
，尽管可以添加卡尔曼滤波器来估计噪声或未测量状态。
(本文冰滞留率β取为：0.98，水箱与建筑物的换热效率）
3.2 经济模型
3.2.1 电能成本
设 
为电价 ($/kWh)，
为净耗电量，能源成本为：
每天的能源价格在前一天下午 4 点发布，因此对于 24 小时模拟，它们是确定性已知的.
对于 
，令 
为受第 i 层需求费用影响的阶段集，令
为第 i 层需求费用之前消耗的最大功率到阶段 k，即在
∩ {0,...,k − 1} 上。变量
使用当月到目前为止的第 i 个峰值需求进行初始化，或者，如果 k = 0 是当月的开始，则使用基于历史数据的目标需求限制。每个
服从动态:
a.本文取初始需求高峰(所有小时)
b.初始需求高峰(（上午 8 点至晚上 10 点）
c.初始需求高峰(（上午 8 点至晚上 6 点）
3.2.2 价格型需求响应成本
一段时间内客户用电量波动率与价格波动率的比值称为电价伸缩系数:
如果实施峰平谷分时电价策略，由于电力用户对电价的反应，不同时期的用电量将发生转移。在本文中，本文采用需求侧响应电价伸缩系数矩阵描述电力需求的变化。
需求侧响应电价伸缩系数矩阵由电能变化与价格变化之比的弹性系数组成。用户用电量不仅与当前时段有关，还与其他时段有关。因此，需求弹性系数分为自弹性系数和交叉弹性系数，可表示为：
式中，
、
分别为
时段的自弹性系数及时段对
时段的交叉弹性系数﹔
、
分别为原系统的负荷量和电价;
、
分别为系统负荷量和电价的改变量。
在采用需求侧响应后,各阶段
负荷变化量
为，如下式：
式中，下角标
、、
代表伸缩系数归属的不同时间段。
综上。采用需求侧响应之后各个时间的负荷需求量矩阵为
所以基于价格型需求响应成本为：
式中，
为分时电价，
低谷电价为，
平段电价为，
高峰电价为.
3.2.3 冷能供应不足惩罚成本
为了避免对负荷冷能供应不足。可以施加惩罚项，这样在所有阶段都能尽可能满足冷负荷的需求，对提供的冷能与所需的冷能的偏差施加二次惩罚 :
这里 
，未满足冷负荷的价格($/(kWh
)，被建模为与第 k 阶段的建筑物占用率成正比，与其热质量成反比.
3.2.4 激励性需求响应成本
可控负荷为一些用电时段具有一定灵活性的用电设备,如洗衣机、可定时电饭煲等，还有本文的制冰机。在调度时段内采用激励型需求响应直接控制方式进行负荷转移,并给予补偿。激励型需求响应成本为：
式中, 
($/kWh)为在激励型需求响应计划中，参与激励型需求响应者获得的价格,
是由需求响应计划计算的第阶段的有功功率损耗。
净阶段成本是电能成本和冷能供应不足惩罚成本的总和:
需求响应成本是基于价格型需求响应成本和基于激励型需求响应成本的总和:
3.3 随机最优控制问题
给定初始状态x0，特殊策略π={μ0，...，
}的总预期成本为:(其中u(K)=μk(x(K)))
其中，对于所有 k ∈T，期望都超过了 w(k)。因此，随机最优控制问题为：
其中约束适用于所有
.
4 算例及运行结果
5 Matlab代码实现
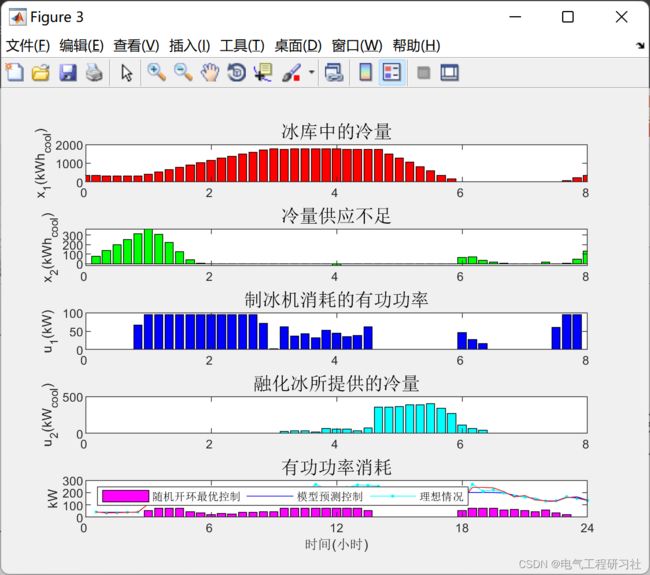
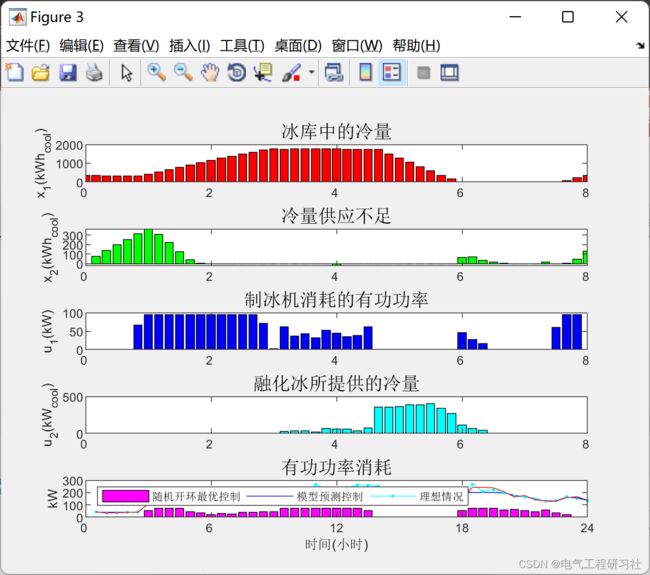
%% 状态和控制时间序列(图 3. MPC 策略下的状态和控制)
%====(1)绘制 x1, 冰罐的充电状态=====
ks = 0 : 1 : N;
figure(iFigure); clf
subplot(5,1,1)
bar(ks,x(1,:),'r')
title('冰库中的冷量', 'FontSize', titleSize)
ylabel('x_1(kWh_{cool})')
set(gca,'XLim',[0,N],'XTick',0:12:N,'XTickLabel',0:2:round(N/2))
%====(2)绘制x2, 为建筑冷却不足(kWhcool）即前阶段所有未满足的冷却负荷的总和（滞后冷却负荷、积压的冷负荷。）
subplot(5,1,2)
bar(ks,x(2,:),'g') %绘制阶梯图
title('冷量供应不足', 'FontSize', titleSize)
ylabel('x_2(kWh_{cool})')
set(gca,'XLim',[0,N],'XTick',0:12:N,'XTickLabel',0:2:round(N/2))
%=====(3)绘制u1, 制冰机消耗的功率。======
subplot(5,1,3)
bar(ks(1:end-1),u(1,:),'b')
title('制冰机消耗的有功功率', 'FontSize', titleSize)
ylabel('u_1(kW)')
set(gca,'XLim',[0,N],'XTick',0:12:N,'XTickLabel',0:2:round(N/2))
%====(4)绘制u2, 冰融化提供的冷却。=====
subplot(5,1,4)
bar(ks(1:end-1),u(2,:),'c')
title('融化冰所提供的冷量', 'FontSize', titleSize)
ylabel('u_2(kW_{cool})')
set(gca,'XLim',[0,N],'XTick',0:12:N,'XTickLabel',0:2:round(N/2))
%======绘制u3, 主制冰机消耗的功率。=====
subplot(5,1,5)
bar(ks(1:end-1),u(3,:),'m')
title('主制冰机消耗的有功功率', 'FontSize', titleSize)
ylabel('u_3(kW)')
set(gca,'XLim',[0,N],'XTick',0:12:N,'XTickLabel',0:2:round(N/2))
xlabel('时间(小时)')
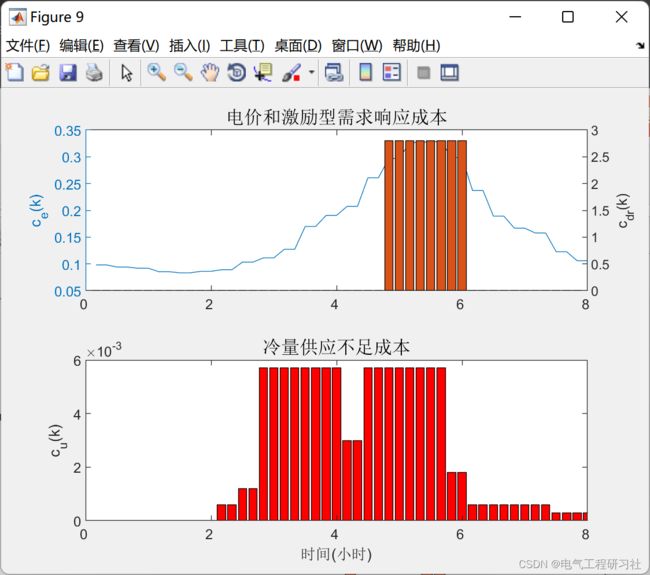
%% 电力和成本时间序列；成本条形图（图 4. MPC 策略下的电力和成本）
%该模块绘制了耗电量及其基线，以及阶段成本和总成本条形图。
%==(1)绘制总电力、其基线，以及如果所有冷负荷直接由主冷水机组（称为pNaive）满足，所消耗的有功功率。===
% pNaive = w(1,:)./params.kMain + w(2,:);
% figure(iFigure+1); clf
% subplot(2,1,1)
% hold on
% plot(ks(1:end-1), u(1,:) + u(3,:) + w(2,:), 'c.-') %MPC
% plot(ks(1:end-1), params.pBase, 'b') %OLOC方法,不考虑DR
% %plot(ks(1:end-1), pNaive, 'r') %pNaive = (w(1,:)./TSDRparams.kMain + w(2,:));如果所有冷负荷直接由主冷水机组（称为pNaive）满足
% set(gca,'XLim',[0,N],'XTick',0:12:N,'XTickLabel',0:6:round(N/2), ...
% 'YLim',[0,50*ceil(max(pNaive)/50)])
% title('有功功率消耗', 'FontSize', titleSize)
% ylabel('有功功率（kW）')
% legend(legLabel,'随机开环最优控制','理想情况', ... %,, '随机开环最优控制', '冷负荷全部由制冰机供冷',
% 'Location', 'SouthEast', 'Orientation', 'Horizontal')
% box on
%%完整代码：qq：207962168
%======(2)阶段成本和总成本条形图。==========
% figure(iFigure+2); clf
figure(iFigure+1);
%subplot(2,1,2)
barsToPlot = [costs.energyCosts', costs.DRcosts', costs.disutilityCosts'];
bar(0:N-1, barsToPlot, 'stack')
title('成本', 'FontSize', titleSize)
xlabel('时间(小时)')
ylabel('成本')
legend('电能成本', '激励型需求响应成本', '冷量供应不足惩罚成本', ...
'Location', 'SouthWest', 'Orientation', 'Horizontal')
set(gca, 'XLim', [0,N], 'XTick',0:12:N,'XTickLabel',0:6:round(N/2))
博主课外兴趣：中西方哲学，送予读者：
做科研，涉及到一个深在的思想系统，需要科研者逻辑缜密，踏实认真，但是不能只是努力，很多时候借力比努力更重要，然后还要有仰望星空的创新点和启发点。当哲学课上老师问你什么是科学，什么是电的时候，不要觉得这些问题搞笑，哲学就是追究终极问题，寻找那些不言自明只有小孩子会问的但是你却回答不出来的问题。在我这个专栏记录我有空时的一些哲学思考和科研笔记：科研和哲思。建议读者按目录次序逐一浏览，免得骤然跌入幽暗的迷宫找不到来时的路，它不足为你揭示全部问题的答案，但若能让人胸中升起一朵朵疑云，也未尝不会酿成晚霞斑斓的别一番景致，万一它居然给你带来了一场精神世界的苦雨，那就借机洗刷一下原来存放在那儿的“真理”上的尘埃吧。
或许，雨过云收，神驰的天地更清朗.......
博主优势：博客内容尽量做到思维缜密，逻辑清晰，为了方便读者，博主专门做了一个专栏目录，整个专栏只放了一篇文章，足见我对其重视程度：博主专栏目录。做到极度细致，方便大家进行学习！亲民！！！还有我开了一个专栏给女朋友的，很浪漫的喔，代码学累的时候去瞧一瞧，看一看：女朋友的浪漫邂逅。有问题可以私密博主，博主看到会在第一时间回复。
6 写在最后
部分理论引用网络文献，若有侵权请联系博主删除。