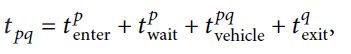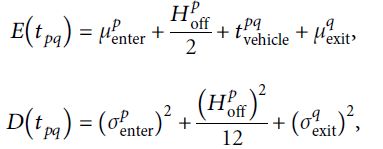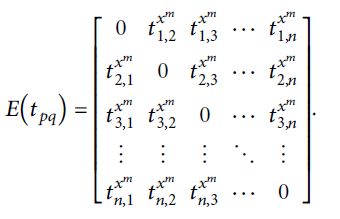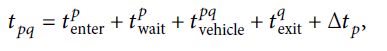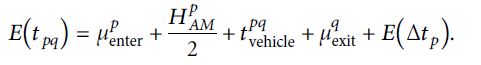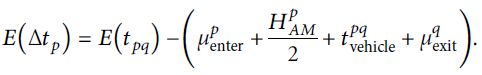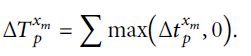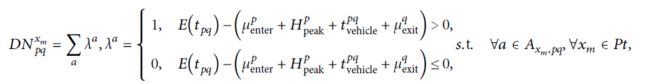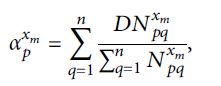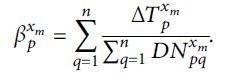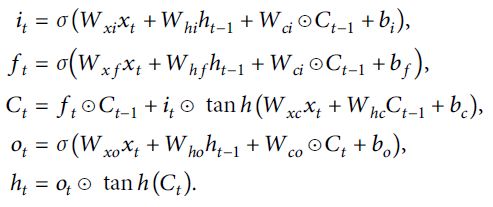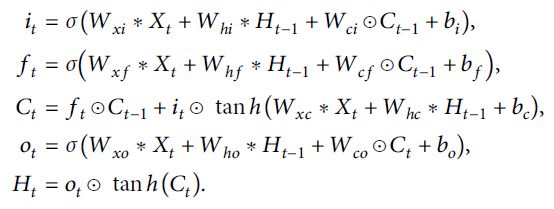基于Conv-LSTM网络的地铁乘客拥堵延误预测深度学习模型
![]()
1 文章信息
![]()
《A Deep Learning Model with Conv-LSTM Networks for Subway Passenger Congestion Delay Prediction》。2020年5月发表在《Journal of Advanced Transportation》上的文章。
![]()
2 摘要
![]()
当城市轨道交通在高峰时段面临大量通勤乘客时,由于地铁满载运行,乘客往往会等待下一班列车,从而导致乘客的整体出行时间延迟。地铁车站拥挤延误的计算和预测可以指导运营部门和乘客做出更好的规划和选择。文章采用一种基于深度学习技术的新方法对地铁站的拥挤延误进行评估。首先,使用自动售检票(AFC)系统数据来评估车站的拥堵延误。利用卷积长短时记忆(Conv-LSTM)网络提取时空特征,解决了网络结构中地铁拥堵延误的短期预测问题。时空变量包括进站客流、出站客流、延误乘客人数和平均延误时间。作为一个时空序列,在端到端训练模型中,输入和预测目标都是时空三维张量。以重庆市轨道交通为例,验证了该方法的有效性。实验结果表明,Conv-LSTM在捕捉空间和时间相关性方面优于基准模型。
![]()
3 介绍
![]()
文章的主要贡献如下:(1)在利用AFC数据计算乘客出行时间的基础上,利用控制变量的思想消除干扰因素,利用高峰时段的实际出行时间与非高峰时段的正常出行时间之差来评价乘客拥挤延误。(2) 用图像和时间序列表示整个网络中地铁客流的拥挤延误。其中,图像包含相邻站点间拥堵延误的空间传播,时间序列包含地铁站点拥堵延误的时间相关性。(3) 将传统的全连接长短时记忆(FC-LSTM)网络思想扩展到卷积长短时记忆(Conv-LSTM)网络,该网络在输入到状态和状态到状态的转换中都具有卷积结构,并且可以有效地捕获拥堵延迟的时空相关性。(4) 计算并预测了整个重庆地铁网络的拥堵延迟,并通过运行数据集验证了该方法的有效性。与传统的客流预测研究不同,传统的客流预测研究往往局限于车站或线路层面的预测。
![]()
4 方法
![]()
(1)利用AFC刷卡数据进行拥堵延迟计算
延迟表示为实际行程时间和正常行程时间之间的差值,由乘客拥挤引起的出行时间的增加称为拥挤延误,这是文章的主要研究对象。拥挤延迟主要由步行延迟和等待延迟组成。(1) 步行延误的主要原因包括:客流拥挤导致的出行缓慢、设备容量限制导致的排队、车站客流组织调整导致的出行距离增加。(2) 候车延误的主要原因是满载率高,乘客无法及时上车。因此,文章采用控制变量的思想,选取特定的日期来消除其他因素(列车延误和信号故障)的干扰,重点研究客流拥挤对出行时间延误的影响。
对于出行过程中需要换乘的乘客,只能通过AFC数据了解乘客进出车站的位置,无法确定乘客在哪里换乘。此外,当乘客的出行时间因乘客拥挤而增加时,无法判断增加的出行时间是发生在始发站还是中转站。因此,在评价车站拥挤程度时,以非换乘旅客为研究对象。如果这部分旅客出现拥堵延误,也可以判断同期进站的非换乘旅客也将面临同样的拥堵情况。
非高峰时间段或正常行驶时间
假设在非繁忙时间,由于车厢或站台的乘客挤塞,乘客不会留在车上。在这种情况下,乘客的等待时间近似为均匀分布U(0,Hnormal),乘客的最大等待时间为非高峰时段的发车间隔。由于乘客的步行速度近似正常,假设乘客的入站步行时间tenter和出站步行时间texit服从正态分布N(μ,σ2)。
一些研究人员认为,对于同一站,进入和离开站台的路径是相同的,所以他们设定步行时间进入和离开站台的时间是相同的值。然而,通过调查,发现一些车站的乘客进出站台的路线不同,乘客进出站台时在站台上的方向不同,楼梯的通行能力也不同。因此,文章分别计算和分析了步行进入和离开站台的时间。对于p站,乘客进出站台的步行时间可设置为tpenter和tpexit。
采取不换乘路线(p∼q) 作为研究对象,总行程时间为:
根据每个行程时间元素的独立性,行程时间的平均值和方差可由下式给出:
时间范围可分为k个周期x1, x2,…,xk。对于xm车站进站的乘客,总行程时间可通过以下公式得出:
拥堵延误高峰期
拥挤延误是指由于车站和车厢内的客流拥挤而导致的额外出行时间。主要包括步行路段客流拥堵造成的额外步行时间和等待路段客流拥堵造成的额外等待时间。
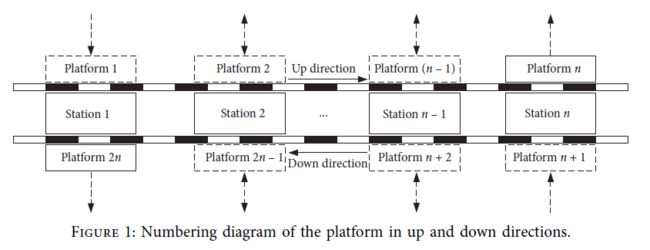
对于同一时间点的同一车站,由于上下方向不同,乘客的等待情况也不同。如图1所示,文章分别计算了各车站上下方向的站台拥堵延误时间。对于有n个车站的l线,站台数量为2n。
采取不换乘路线(p∼q) 作为研究对象,总行程时间为:
根据每个行程时间元素的独立性,行程时间的平均值和方差为:
利用前文得到的步行时间μp和μq,可得到p站乘客的拥挤延误时间。
车站拥堵研究的时间范围可分为k个周期x1, x2,…,xk。对于xm车站进站的乘客,总行程时间可通过以下公式得出:
如果乘客平均到达站台,平均等待时间等于发车间隔的一半。换言之,即使站台没有挤塞情况,乘客的候车时间也有一半超过发车间隔的一半。因此,对于某一特定乘客,即使Δtxmp>0,也不能确定该乘客是否存在拥堵延误。为避免这部分乘客可能造成拥堵延误乘客数计算错误,所以采用整个出发间隔作为无拥堵延误乘客的最大等待时间。拥堵延误整个发车间隔的,视为延误。被延误的旅客人数计算公式如下:
对于p站,在xm期间发生拥堵延误的乘客比例为:
对于p站,在xm时段内乘客进入车站的平均拥堵延误时间为:
(2)使用深度学习的方法进行预测
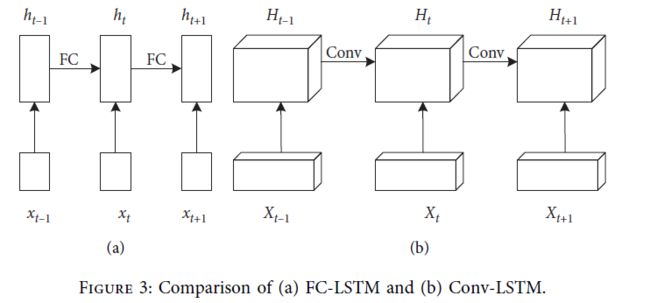
客运拥堵延误具有复杂的时空特征。车站某一时刻的拥堵延误可以从两个方面来解释。从时间维度来看,下一时段的乘客拥堵延误可以看作是上一时段乘客拥堵延误的延续。从空间维度来看,车站的乘客拥挤延误受到相邻车站拥挤延误的影响,相邻车站拥挤延误具有一定的空间相关性。因此,我们使用Conv - LSTM来处理地铁乘客拥挤延迟的空间依赖性、时间依赖性和网络拓扑特性。在本节中,将简要回顾传统的FC-LSTM结构,然后解释 Conv- LSTM的深度学习体系结构和优点。
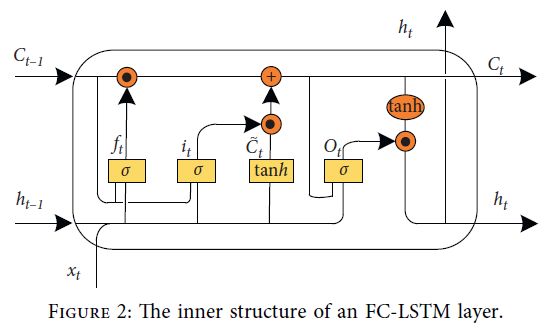
FC-LSTM
FC-LSTM的框架图为:
FC-LSTM的公式为:
由于FC-LSTM的内部门是通过类似的前馈神经网络计算的,这种结构可以很好地处理时间序列数据,但对于空间数据,会带来冗余。这是因为空间数据具有很强的局域性,而FC-LSTM无法描述这些局域性。
Conv-LSTM
为了获得更好的时空关系,将传统的FC-LSTM思想扩展到Conv-LSTM。方法是将FC-LSTM的输入到状态和状态到状态用卷积代替前馈计算。通过将多个Conv-LSTM层叠加形成预测结构,可以建立一个用于短期地铁拥堵延迟预测的端到端的训练模型。Conv-LSTM可以克服传统LSTM在网络空间依赖性方面的缺点。与传统的LSTM相比,Conv-LSTM将所有的输入、输出、隐藏状态和各种门从一个二维矢量转换为一个三维张量。ConvLSTM与FC-LSTM的比较如图3所示。
地铁拥挤延误系统在空间区域中的网格由P行和Q列组成。网格中每个具有地铁站的单元具有随时间变化的Z测量标度。因此,任何时候的信息都可以用张量X表示∈RZ×P×Q,其中R是观察到的特征域。Conv-LSTM通过其局部邻居的输入及其过去的状态来确定网格中单元的未来状态。公式如下:
在这一部分中,可以将Conv-LSTM作为模型来处理二维网格中的特征向量,可以根据网格中周围点的特征来预测中心网格的特征。因此,文章在时空变量下对地铁拥挤延误系统进行短期预测。
Conv-LSTM的训练步骤如下:
![]()
5 实验
![]()
(1)数据集
文章以重庆地铁网为例对模型进行了验证。在重庆地铁系统中,乘客需要在每个地铁站的自动售检票系统上输入智能卡信息。AFC系统记录每个乘客的出入口信息(例如,交易时间和车站ID)。卡数据示例如表1所示。文章选取了重庆地铁2018年9月和10月40个工作日的运营数据。首先,计算地铁乘客延误率和拥挤延误指数。计算预测结果的RMSE、MAE和R2值,以评估Conv LSTM模型的能力和有效性。
(2)结果
需要将地铁网络图分成许多小单元,并确保每个小单元最多包含一个地铁站。因此,文章将地铁网络单元的行和列值取为64。此外,数据集将分为两部分:第一部分是训练数据(35天),第二部分是测试数据(5天)。将测试Conv-LSTM模型的不同层,以确定最佳结构。通过使用历史观测数据,如进出车站的乘客人数、延误率和平均延误时间,预测未来延误率。
通过对重庆地铁网络延误率的实际情况和延误率的预测情况进行可视化,验证了模型的有效性。
![]()
6 总结
![]()
文章在分析地铁出行时间延误原因的基础上,运用控制变量的思想,提出了地铁网络层面的乘客拥挤延误计算方法。考虑到站间客流拥堵具有传播性,车站拥堵不仅与车站历史拥堵有关,还与相邻车站的拥堵有关。因此,结合乘客拥挤的时空特征,采用基于CNN和FC-LSTM的改进深度学习方法Conv-LSTM对地铁车站拥挤延误进行短期预测。Conv-LSTM不仅保留了FC-LSTM的优点,而且由于其独特的卷积结构,适用于时空数据。文章使用各种基准模型来评估所提出模型的性能。试验结果表明,Conv-LSTM能较好地解决地铁车站客流拥挤延误预测问题。
![]()
Attention
![]()
如果你是轨道交通、道路交通、城市规划相关领域的,可以加微信:Dr_JinleiZhang,备注“进群”,加入交通大数据交流群!希望大家共同进步!