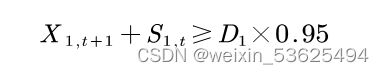2022华数杯B题论文思路分析+完整代码（水下机器人组装计划）(一二问答案接出来和标准答案一样)（问题三四逼近正确答案）（完整论文，代码可直接跑）

 写在前面：学校最近搞数学建模竞赛培训，以2022华数杯B题作为训练题目，在查资料过程中发现网上没有哪一篇论文解出了正确答案，而我们组利用Lingo软件准确的解出了正确答案，但是在第三问时，由于决策的变量激增，基于Lingo的模型已经无法解出，所以选择使用模拟退火算法进行解算。另外在文末给出了官方的标准答案。代码也在文末给出，自行复制，可直接运行。（如有读者发现错误，请及时联系指正。）另外，本文仅供大家参考交流使用^^。

还有就是，下面的论文中的表的标号会出现错误是因为把附录中的表部分粘到了正文中，排版正确文章见pdf。

不用付费，直接下（2022华数杯B题论文思路分析+完整代码（水下机器人组装计划）(一二问答案接出来和标准答案一样)（问题三四逼近正确答案）（完整论-其它文档类资源-CSDN下载）

基于线性规划的水下机器人组装计划的研究与分析

摘要

本文主要研究了水下机器人组装计划问题。主要基于Lingo软件建立线性规划模型，完成了对问题一、问题二和问题四中周生产计划的求解，并且利用Matlab软件编写模拟退火算法对第三问中检修日进行确定，最后利用SPSS软件，采取季节性一元预测模型对问题四中的历史数据进行预测。

针对问题一，从题目中提炼出五个约束条件：在周一和周日没有任何库存；忽略小组件从采购到组装与从小组件组装完成到组装WPCR的中间时间；每日的WPCR需求量必须按时、按量完成（也可以提前完成）；A、B、C的生产总工时必须符合总工时限制条件；每天只采购能满足当天需求量的小组件数量，不进行小组件的存储，不产生小组件的库存费用。基于上述条件分三步建立线性规划模型“确定决策变量——确定目标函数——确定约束条件”，对问题一进行求解。结果显示按照求解出的生产计划，可使得生产总成本最小，最小值为6260.9元。

针对问题二，从题目中提炼出四个约束条件：A、B、C的生产总工时必须符合总工时限制条件；组件A、B、C需要提前一天生产入库才能组装WPCR，A1、A2、A3、B1、B2、C1、C2、C3也需要提前一天生产入库才能组装A、B、C；对于WPCR而言，某天的需求量可由当天的组装量和前一天的库存量共同提供；本周日与上个周日的相比较，各个变量的相关数值应该完全相等。基于上述条件分三步建立线性规划模型“确定决策变量——确定目标函数——确定约束条件”，对问题二进行求解。结果显示按照求解出的生产计划，可使得生产总成本最小，最小值为177212.5元。

针对问题三，从题目中提炼出四个约束条件：在30周210天内设置7次检修，并且每次检修一天，任意两次检修之间间隔6天以上；检修日停工停产，检修日的订单只能提前安排生产；检修之后设备生产能力提高，检修后的第一天A、B、C生产总工时限制将会放宽10%，随后逐日减少放宽2%的比例，直至为0；总工时限制。基于上述约束条件，本文选择使用模拟退火算法进行优化求解。

针对问题四，从题目中提炼出两个约束条件：以过去30周数据作为历史周订单数据；既保障每天的WPCR订单均以95%以上的概率正常交付，又保障每周的WPCR订单以85%以上的概率正常交付；基于上述约束条件，首先采取基于一元时间序列预测模型对WPCR未来某周7天的订单数进行预测，再以预测结果通过问题二中建立的模型求解稳妥的单周生产计划。

关键词：线性规划 Lingo 模拟退火算法 SPSS 优化 Matlab

1. 问题重述

自来水管道清理机器人（WPCR）由3个A组件、4个B组件和5个C组件组装而成；其中A组件由6个A1组件、8个A2组件和2个A3组件组装而成，B组件由2个B1组件和4个B2组件组装而成，C组件由8个C1组件、2个C2组件和12个C3组件组装而成。

该工厂每次生产计划期为一周（即每次按照每周7天的订购数量实行订单生产），并且只有WPCR有外部需求，其他组件不对外销售。另外，A 、B 、C的工时消耗分别为 3 时/件、5 时/件和 5 时/件，表5为每天的WPCR外部 需求数及关键设备总工时限制。

在生产WPCR时需要付出生产准备费用和库存费用，生产准备费用和库存费用数据见表6。另外，所有订单到期必须全部交货，轻易不能有缺货事件发生。

请尝试建立数学模型讨论下列问题：

（1）工厂周一开始时和周日结束时不能有任何组件库存，每天各组件都可立刻用于组装。在使总成本最小的情况下，制定每周7天的生产计划，结果填入表一。

（2）组件A、B、C需要提前一天生产入库才能组装WPCR，A1、A2、A3、B1、B2、C1、C2、C3也需要提前一天生产入库才能组装A、B、C。在使总成本最小的情况下，制定每周7天的生产计划，结果填入表二。

（3）在问题二的基础上，工厂要在30周210天里设置7次停工检修，每次停工检修一天。检修之后关键设备生产能力有所提高，检修后的第一天A、B、C生产总工时限制将会放宽10%，随后逐日减少放宽2%的比例，直至为0(如第一天放宽10%，第二天就放宽8%，...)。检修日的订单必须提前安排，任意两日检修要相隔6天以上。30周的WPCR外部需求数据见表7。在使总成本最小的情况下，制定7次检修的检修日期，结果填入表三。

（4）将30周的WPCR外部需求数据作为历史订单数据，在保障每天的WPCR订单均以95%以上的概率保证正常交付，又能够以85%以上的概率保证整周的WPCR订单能正常交付的条件下，制定稳妥的周生产计划，结果填入表四。

1. 问题分析

该题目是以自来水管道清理机器人的组装为背景的多变量约束规划问题，问题一到问题四，逐步增加约束条件，本文采取先基于问题一简单的约束条件建立初级数学模型，再根据逐步增加的约束条件对建立的初级模型进行修改完善，最后完成对问题的求解。

2.2 对问题一的分析

问题一要求制定每周七天的生产计划，使得总成本最小，并且给出如下约束条件：

1. 在周一和周日没有任何库存；
2. 忽略小组件从采购到组装与从小组件组装完成到组装WPCR的中间时间；
3. 每日的WPCR需求量必须按时、按量完成（也可以提前完成）；
4. A、B、C的生产总工时必须符合总工时限制条件；

另外根据题目中条件“每天采购的组件马上就可用于组装，组装出来的组件也可以马上用于当天组装成WPCR”，有充分的理由可以推导出如下结论：“每天的小组件（指的是组装A/B/C所需要的组件）没有必要进行储存，即这些小组件不需要付库存费用”，理由如下：如果为了省下某组件的开工费，需要在前一天储存好能满足第二天WPCR生产的需要，而此时对应该部件储存的费用已经远远地大于了开工费。所以添加如下约束条件：

1. 每天只采购能满足当天需求量的小组件数量，不进行小组件的存储，不产生小组件的库存费用。

基于上述约束条件，本文认为解决该问题的模型方法由以下三个步骤组成：

1. 确定决策变量与相关符号说明，其目的主要是对题目中的条件进行数学化处理，找出决定目标函数大小的决策变量；
2. 确定目标函数，主要是通过决策变量建立目标函数的表达式；
3. 确定约束条件，对已经分析出来的约束条件用数学符号进行表达。

2.3 对问题二的分析

问题二仍然要求在总成本最低情况下，制定每周7天的生产计划，并给出如下约束条件：

1. A、B、C的生产总工时必须符合总工时限制条件；
2. 组件A、B、C需要提前一天生产入库才能组装WPCR；A1、A2、A3、B1、B2、C1、C2、C3也需要提前一天生产入库才能组装A、B、C；

另外，根据约束条件（2）可以推导出如下约束条件：

1. 对于WPCR而言，某天的需求量可由当天的组装量和前一天的库存量共同提供；

然后根据问题二中的信息“在连续多周生产情况下”和“每周的WPCR需求和关键设备工时限制以及每次生产准备费用和单件库存费用数据见表5、表6”可以得出如下结论：

1. 本周日与上个周日的相比较，各个变量的相关数值应该完全相等；

2.4 对问题三的分析

问题三要求在总成本最低的情况下，确定7次检修的检修日期，并给出约束条件如下：

1. 在30周210天内设置7次检修，并且每次检修一天，任意两次检修之间间隔6天以上；
2. 检修日停工停产，检修日的订单只能提前安排生产；
3. 检修之后设备生产能力提高，检修后的第一天A、B、C生产总工时限制将会放宽10%，随后逐日减少放宽2%的比例，直至为0；
4. 总工时限制。

本文在求解问题三时，在采用问题一中建立模型的整体思路“确定决策变量——确定目标函数——确定约束条件”时，遇到变量数量过多的问题，因此选择使用模拟退火算法进行求解。

2.5 对问题四的分析

问题四要求在未知WPCR外部需求订单的前提下，给公司制定稳妥的单周生产计划，并给出如下约束条件：

1. 以过去30周数据作为历史周订单数据；
2. 既保障每天的WPCR订单均以95%以上的概率正常交付，又保障每周的WPCR订单以85%以上的概率正常交付；

因此，本文基于上述约束条件，首先采取基于一元时间序列预测模型对WPCR未来某周7天的订单数进行预测，再以预测结果通过问题二中建立的模型求解稳妥的单周生产计划。

3、模型假设

1. 生产过程中，不会因为工厂停电、机械故障等突发情况打断生产；
2. 工厂资金流正常，不会因为缺乏资金而影响生产；
3. 只有最终WPCR装置有外部需求，其他组件不对外销售；
4. 机器人的需求按计划而定，不受市场价格波动影响；
5. WPCR的外部需求量不会临时发生改变。

4、符号说明

5、模型的建立与求解

5.1 问题一模型的建立与求解

5.1.1 确定决策变量与相关符号说明

为了便于后续计算与表示，本文首先对WPCR装置及其所有组件进行编号处理，编号结果如下：

表 1 WPCR装置及各组件编号

名称	编号i
WPCR	1
A	2
B	3
C	4
A1	5
A2	6
A3	7
B1	8
B2	9
C1	10
C2	11
C3	12

另外对周一到周日进行编号，编号结果如下：

表 2 周一到周日对应编号

名称	编号t
周一开始的时候	1
周一结束的时候	2
周二结束的时候	3
周三结束的时候	4
周四结束的时候	5
周五结束的时候	6
周六结束的时候	7
周日结束的时候	8

接着设出相关变量来表示题目中对应信息，列表如下：

5.1.2 确定目标函数

5.1.3 确定约束条件

          

5.1.4 问题一的求解

根据上述步骤，本文通过Lingo软件进行进行编程解算（代码见附录一），得到如下结果：

表 5 WPCR及各组件每日剩余量

日期	WPCR剩余量	A剩余量	B剩余量	C剩余量	生产准备费用	库存费用
周一	44	0	0	1	1200	221.7
周二	8	0	344	1	340	557.7
周三	51	0	20	0	860	285
周四	11	0	20	0	0	85
周五	22	0	1	0	1200	111.5
周六	40	0	0	0	1200	200
周日	0	0	0	0	0	0
总和	176	0	385	2	6260.9

表 6 问题一的结果

日期	WPCR组装数量	A组装数量	B组装数量	C组装数量	生产准备费用	库存费用
周一	83	249	332	416	1200	221.7
周二	0	0	344	0	340	557.7
周三	81	243	0	404	860	285
周四	0	0	0	0	0	85
周五	48	144	173	240	1200	111.5
周六	51	153	203	255	1200	200
周日	0	0	0	0	0	0
总和	263	789	1052	1315	6260.9

按照表6制定每周七天的生产计划，可使得生产总成本最小，最小值为6260.9元。

model:

sets:
si/1..4/:P,C1;
st/1..8/:B,C2,T1,D;
stemp/1..7/:;
lit(si,st):X,S,K;
endsets

data:
P=240,270,340,350;
T1=0,4500,2500,2750,2100,2500,2750,1500;
D=0,39,36,38,40,37,33,40;
C1=5,2,1.5,1.7;
enddata

min=@sum(st(t):B(t)+C2(t));

@for(lit(i,t):K(i,t)=X(i,t) #gt# 0);
@for(st(t):B(t)=@sum(si(i):K(i,t)*P(i)));
@for(st(t):C2(t)=@sum(si(i):S(i,t)*C1(i)));

!Zero at begin and end;
@for(si(i):S(i,1)=0);
@for(si(i):S(i,8)=0);

@for(st(t)|t #le# 7:S(1,t+1)=X(1,t+1)+S(1,t)-D(t+1));
@for(st(t)|t #le# 7:S(2,t+1)=X(2,t+1)+S(2,t)-3*X(1,t+1));
@for(st(t)|t #le# 7:S(3,t+1)=X(3,t+1)+S(3,t)-4*X(1,t+1));
@for(st(t)|t #le# 7:S(4,t+1)=X(4,t+1)+S(4,t)-5*X(1,t+1));


@for(st(t):3*X(2,t)+5*X(3,t)+5*X(4,t)<=T1(t));

!int limited;
@for(lit:@gin(X));
@for(lit:@gin(S));
@for(lit:@bin(K));

end

5.2 问题二模型的建立与求解

5.2.1 确定决策变量与相关符号说明

5.2.2 确定目标函数

            

5.2.3确定约束条件

                      

 

5.2.4 问题二的求解

根据上述步骤，本文通过Lingo软件进行进行编程解算（代码见附录），得到如下结果：

表 8 问题二的结果

日期	WPCR组装数量	A组装数量	B组装数量	C组装数量	生产准备费用	库存费用
周一	0	246	341	416	630	33737.7
周二	82	0	0	0	750	31296.7
周三	0	300	370	404	280	2101.7
周四	100	0	0	0	420	9899.7
周五	0	0	341	240	480	42572.2
周六	0	243	0	255	300	1686.0
周日	81	0	0	0	740	52318.5
总和	263	789	1052	1315	177212.5

另外WPCR及各大组件的剩余量见下表：

表 9 WPCR及各大组件的剩余量

日期	WPCR剩余量	A剩余量	B剩余量	C剩余量	生产准备费用	库存费用
周一	2	246	358	411	630	33737.7
周二	48	0	30	501	750	31296.7
周三	10	300	400	501	280	2101.7
周四	70	0	0	1	420	9899.7
周五	33	0	341	1	480	42572.2
周六	0	243	341	405	300	1686.0
周日	41	0	17	0	740	52318.5
总和	204	789	1487	1820	177212.5

（各小组件的剩余数量见附录）

由表9可知，按照表9制定每周七天的生产计划，可使得生产总成本最小，最小值为177212.5元。

表 15 各小组件组装数量

日期	A1组装数量	A2组装数量	A3组装数量	B1组装数量	B2组装数量	C1组装数量	C2组装数量	C3组装数量
周一	0	0	0	0	0	4000	1000	6000
周二	1800	2400	600	740	1480	0	0	0
周三	0	0	0	0	0	0	0	0
周四	0	0	0	682	1364	0	0	0
周五	1458	1944	486	0	0	3232	808	4848
周六	0	0	0	0	0	0	0	0
周日	1476	1968	492	682	1364	3288	822	4932
总和	4734	6312	1578	2104	4208	10520	2630	15780

表 16 各小组件剩余数量

日期	A1剩余量	A2剩余量	A3剩余量	B1剩余量	B2剩余量	C1剩余量	C2剩余量	C3剩余量
周一	0	0	0	0	0	4000	1000	6000
周二	1800	2400	600	740	1480	0	0	0
周三	0	0	0	0	0	0	0	0
周四	0	0	0	682	1364	0	0	0
周五	1458	1944	486	0	0	3232	808	4848
周六	0	0	0	0	0	0	0	0
周日	1476	1968	492	682	1364	3288	822	4932
总和	4734	6312	1578	2104	4208	10520	2630	15780

另外，其余具体各变量的解在5.2.4中给出

model:

sets:
si/1..12/:P,C1,N;
st/1..8/:B,C2,D,T1;
lit(si,st):K,X,S,C,E;
endsets

data:
P=240,120,160,180,40,60,50,80,100,60,40,70;
C1=5,2,1.5,1.7,5,3,6,4,5,3,2,3;
T1=4500,2500,2750,2100,2500,2750,1500,4500;
D=39,36,38,40,37,33,40,39;
N=0,3,4,5,6,8,2,2,4,8,2,12;
enddata

min=@sum(st(t)|t#le#7:B(t)+C2(t));

@for(lit(i,t):K(i,t)=X(i,t) #gt# 0);
@for(st(t):B(t)=@sum(si(i):K(i,t)*P(i)));
@for(st(t):C2(t)=@sum(si(i):S(i,t)*C1(i)));

@for(st(t)|t#le#7:S(1,t+1)=X(1,t+1)+S(1,t)-D(t+1));
S(1,1)=X(1,1)+S(1,7)-D(1);

@for(lit(i,t)|(t#le#7)#AND#(i#ge#2):E(i,t+1)=S(i,t)-C(i,t+1));
@for(si(i)|i#ge#2:E(i,1)=S(i,7)-C(i,1));

@for(lit(i,t)|i#ge#2:E(i,t)+X(i,t)=S(i,t));


@for(lit(i,t)|(i#ge#2)#AND#(i#le#4):C(i,t)=N(i)*X(1,t));
@for(lit(i,t)|(i#ge#5)#AND#(i#le#7):C(i,t)=N(i)*X(2,t));
@for(lit(i,t)|(i#ge#8)#AND#(i#le#9):C(i,t)=N(i)*X(3,t));
@for(lit(i,t)|(i#ge#10)#AND#(i#le#12):C(i,t)=N(i)*X(4,t));

@for(st(t):3*X(2,t)+5*X(3,t)+5*X(4,t)<=T1(t));

B(8)=B(1);
C2(8)=C2(1);
@for(si(i):X(i,8)=X(i,1));
@for(si(i):S(i,8)=S(i,1));
@for(si(i):K(i,8)=K(i,1));
@for(si(i):E(i,8)=E(i,1));
@for(si(i):C(i,8)=C(i,1));

@for(lit:@bin(K));
@for(lit:@gin(S));
@for(lit:@gin(X));
@for(lit:@gin(C));
@for(lit:@gin(E));

End

5.3 问题三模型的建立与求解

5.3.1 引入相关变量

                                      

5.3.2 约束条件

约束一：总工时限制：

                            

约束二：检修后总工时限制放宽：

约束三：检修日不产生任何组件：

                               

约束四：保证生产可以继续：

5.3.3 问题三的求解

使用Matlab软件编写模拟退火算法，寻求最优解，其结果如下：

表 10 问题三的结果

第一次	第二次	第三次	第四次	第五次	第六次	第七次	总成本
43	62	94	157	171	178	190	5655900

clear
clc
%每天WPCR需求量
WPCR=[39 36 38 40 37 33 40
39 33 37 43 34 30 39
42 36 35 38 36 35 41
38 36 36 48 34 35 39
38 36 40 40 40 34 39
40 30 36 40 34 36 37
41 36 41 41 38 29 43
33 31 40 42 42 30 40
35 36 38 33 35 37 41
43 35 42 37 36 33 39
38 32 41 36 40 31 34
37 37 41 39 38 35 38
38 38 33 42 42 29 33
39 37 44 38 35 36 38
40 39 38 38 37 34 44
35 36 38 39 39 39 39
43 28 39 41 38 30 38
35 37 40 41 40 35 41
36 35 40 41 37 38 36
37 38 39 41 38 37 44
37 37 37 36 39 33 41
39 37 42 37 36 28 43
40 32 35 45 40 34 43
38 36 37 36 40 28 45
38 40 38 36 35 40 42
31 31 44 36 31 36 40
40 36 34 43 35 32 39
33 33 36 41 34 38 40
35 34 37 37 39 36 40
37 41 39 41 36 32 44];
WPCR=reshape(WPCR',210,1)';
WPCR=[WPCR,WPCR(1:2)];
%一个WPCR队ABC需求比例
A_x=3;
B_x=4;
C_x=5;
D_x=[6;8;2;2;4;8;2;12];
%每天总工时
T=repmat([4500 2500 2750 2100 2500 2750 1500],1,30);
T=[T(end),T,T(1)];
%ABC单位工时消耗
TA=3;
TB=5;
TC=5;
%生产准备费用：A A1 A2 A3 B B1 B2 C C1 C2 C3
W=[240 120 40 60 50 160 80 100 180 60 40 70];
%单件库存费用：A A1 A2 A3 B B1 B2 C C1 C2 C3
C=[5 2 5 3 6 1.5 4 5 1.7 3 2 3];

%模拟退火-粒子群算法
T0=100; %初始化温度值
T_min=1; %设置温度下界
alpha=0.9; %温度的下降率
c1=0.4;c2=0.6; %学习因子
wmax=0.6;wmin=0.4; %惯性权重
num=2; %颗粒总数
X=[];
A=[];
F=[];
for i=1:num
    [X(i,:),A(i,:),F(i,1)]=chushihua3(WPCR,A_x,B_x,C_x,T,TA,TB,TC,W,C,D_x);
end
%以最小化为例
[bestf,a]=min(F);
bestx=X(a,:);
bestA=A(a,:);
trace(1)=bestf;
while(T0>T_min)
    XX=[];
    FF=[];
    AA=[];
 for i=1:num
        [XX(i,:),AA(i,:),FF(i,1)]=chushihua3(WPCR,A_x,B_x,C_x,T,TA,TB,TC,W,C,D_x);
        delta=FF(i,1)-F(i,1);
        if delta<0
            F(i,1)=FF(i,1);
            X(i,:)=XX(i,:);
            A(i,:)=AA(i,:);
        else
            P=exp(-delta/T0);
            if P>rand
                F(i,1)=FF(i,1);
                X(i,:)=XX(i,:);
                A(i,:)=AA(i,:);
            end
        end  
    end
    fave=mean(F);
    fmin=min(F);
    for i=1:num
        %权重更新
        if F(i)<=fave
            w=wmin+(F(i)-fmin)*(wmax-wmin)/(fave-fmin);
        else
            w=wmax;
        end
        [~,b]=min(F);
        best=X(b,:);%当前最优解
        %粒子群算法限制最多找10次位置
        m=1;
        flag=0;
        while flag==1
        v=w.*randn(1,28)+c1*rand*(best-X(i,:))+c2*rand*(bestx-X(i,:));%速度
        XX(i,:)=round(X(i,:)+v);%更新位置
        XX(i,:)=max(XX(i,:),0);%不能小于0
        %检验，不满足条件则返回之前的变量
        x=reshape(XX(i,:)',7,4)';%重新排列矩阵维度
        J=jianyan3(x,AA(i,:),WPCR,A_x,B_x,C_x);
        if (length(find((sum(x(2:4,:).*[TA;TB;TC],1)-T)>0))==0 & sum(x(1,:))>=sum(WPCR) & J==0) | m==10
            XX(i,:)=X(i,:);
        else
            m=m+1;
        end
        end
        %计算目标函数
        FF(i,1)=fun3(XX(i,:),AA(i,:),WPCR,A_x,B_x,C_x,W,C,D_x);
        %更新最优
        if FF(i,1)

function [X,b,F]=chushihua3(WPCR,A_x,B_x,C_x,T,TA,TB,TC,W,C,D_x)
%初始化变量、计算目标函数值，小件提前两天，大件提前1天
flag1=0;
while flag1==0
%检修
flag3=0;
while flag3==0
    A=zeros(1,length(WPCR));
    a=10+randperm(length(WPCR)-20);
    aa=a(1:7);
    A(aa)=1;
    b=find(A==1);
    c=b(2:end)-b(1:end-1);
    d=find(c<6);
    if length(d)==0
        flag3=1;
    end
end
%检修后提高效率
AA=[];%对应的时间
for i=1:length(b)
    AA=[AA,b(i)+1:b(i)+5];
end
G=repmat([1.1 1.08 1.06 10.4 1.02],1,length(b));
TT=T;
TT(AA)=TT(AA).*G;
X=[];
nn=2;%延迟天数
flag1=1;
KC_WPCR=zeros(1,length(WPCR)+nn);%记录每天WPCR库存
KC=zeros(3,length(WPCR)+nn);%记录每天ABC库存
KC_x=zeros(8,length(WPCR)+nn);%记录每天ABC小件库存
SY_WPCR=zeros(1,length(WPCR)+nn);%记录每天交付WPCR情况
SY=zeros(3,length(WPCR)+nn);%记录每天使用ABC情况
% SY_x=zeros(8,length(WPCR)+nn);%记录每天使用ABC小件情况
SC_WPCR=zeros(1,length(WPCR)+nn);%记录每天组装WPCR情况
SC=zeros(3,length(WPCR)+nn);%记录每天生产ABC情况
SC_x=zeros(8,length(WPCR)+nn);%记录每天生产ABC小件情况
for i=1:length(WPCR)%循环遍历每个WPCR
    if i==1%假设第一天刚好满足WPCR
        sub=[A_x,B_x,C_x].*WPCR(i);%求出每天的WPCR最小ABC需求量
        up=sub;
    else
        sub=max([A_x,B_x,C_x].*WPCR(i)-KC(:,i+nn-1)',0);%除了第一天，每天减去前一天的库存则为当天至少增加的需求量
        up=[];
        up(1)=fix((T(i)-sub([2,3])*[TB;TC])/TA);%BC最低供应时，A最大供应量
        up(2)=fix((T(i)-sub([1,3])*[TA;TC])/TB);%AC最低供应时，B最大供应量
        up(3)=fix((T(i)-sub([1,2])*[TA;TB])/TC);%AC最低供应时，B最大供应量
        up=min(up,fix(T(i)./([A_x,B_x,C_x]*[TA;TB;TC])*2).*[A_x,B_x,C_x]);
    end
    %前面的变量会影响后面的变量范围，可能会出现上up小于sub的情况，毕竟有最大工时限制
    if length(find((up-sub)<0))>0%如果出现则重新生成
        flag1=0;
        continue
    end
    flag2=0;
    while flag2==0
        x=[randi([sub(1),up(1)]),randi([sub(2),up(2)]),randi([sub(3),up(3)])];%在区间内随机生成整数
        if i==1
            flag2=1;
        elseif i>1
            if x*[TA;TB;TC]<=T(i)%需求量必须满足在工时限制内
                flag2=1;
            end
        end
    end
    %每天组装的WPCR
    if i==1
        s=WPCR(i);%可组装最小数量
        u=min(fix(x./[A_x,B_x,C_x]));%可组装最大数量
    else
        s=max(WPCR(i)-KC_WPCR(i+nn-1),0);
        u=min(fix([x+KC(:,i+nn-1)']./[A_x,B_x,C_x]));
    end
    if u0))=1;
X2=[repmat(X1(2,:),3,1);repmat(X1(3,:),2,1);repmat(X1(4,:),3,1)];
X2(:,b)=0;
%最优情况，小件无库存但是有生产准备费用
f1=(sum(X1.*[W(1);W(2);W(6);W(9)],1)+sum(X2.*[W(3:5)';W(7:8)';W(10:12)'],1))';
f2=(sum(X3.*C([1,2,6,9])',1)+sum(X4.*C([3,4,5,7,8,10,11,12])',1))';
F=sum(f1)+sum(f2);

function [F,f1,f2]=fun3(X,b,WPCR,A_x,B_x,C_x,W,C,D_x)
%初始化变量、计算目标函数值
X=reshape(X',212,4);
nn=2;
KC_WPCR=zeros(1,length(WPCR)+nn);%记录每天WPCR库存
KC=zeros(3,length(WPCR)+nn);%记录每天ABC库存
KC_x=zeros(8,length(WPCR)+nn);%记录每天ABC小件库存
SY_WPCR=zeros(1,length(WPCR)+nn);%记录每天交付WPCR情况
SY=zeros(3,length(WPCR)+nn);%记录每天使用ABC情况
% SY_x=zeros(8,length(WPCR)+nn);%记录每天使用ABC小件情况
SC_WPCR=zeros(1,length(WPCR)+nn);%记录每天组装WPCR情况
SC=zeros(3,length(WPCR)+nn);%记录每天生产ABC情况
SC_x=zeros(8,length(WPCR)+nn);%记录每天生产ABC小件情况
for i=1:length(WPCR)%循环遍历每个WPCR
    x=X(i,2:4);
    %更新SC、KC、SY矩阵
    %生产
    if length(find(b==i))==1
        SC_WPCR(i+nn)=0;
    else
        SC_WPCR(i+nn)=X(i,1);
    end
    if length(find(b==i-1))==1
        SC(:,i+nn-1)=0;
    else
        SC(:,i+nn-1)=SC(:,i+nn-1)+x';
    end
    %放库存
    KC_WPCR(i+nn)=KC_WPCR(i+nn-1)+SC_WPCR(i+nn);
    if KC_WPCR(i+nn)<0
        KC_WPCR(i+nn)=0;
    end
    if i==1
        KC(:,i+nn-1)=SC(:,i+nn-1);
    else
        KC(:,i+nn-1)=KC(:,i+nn-1)+SC(:,i+nn-1);
    end
    KC_x(1:3,i+nn-2)=D_x(1:3).*SC(1,i+nn-1);
    KC_x(4:5,i+nn-2)=D_x(4:5).*SC(2,i+nn-1);
    KC_x(6:8,i+nn-2)=D_x(6:8).*SC(3,i+nn-1);
    %使用
    SY_WPCR(i+nn)=WPCR(i);
    SY(:,i+nn)=[A_x;B_x;C_x].*SY_WPCR(i+nn);
    %更新库存
    KC_WPCR(i+nn)=KC_WPCR(i+nn)-WPCR(i);
    KC(:,i+nn)=KC(:,i+nn-1)-SY(:,i+nn);
end
X1=[SC_WPCR(:,nn+1:end-2);SC(:,nn+1:end-2)];%生产
X3=[KC_WPCR(:,nn+1:end-2);KC(:,nn+1:end-2)];%库存ABC
X4=[KC_x(:,nn+1:end-2)];%库存ABC小件
X1(find(X1>0))=1;
X2=[repmat(X1(2,:),3,1);repmat(X1(3,:),2,1);repmat(X1(4,:),3,1)];
X2(:,b)=0;
%最优情况，小件无库存但是有生产准备费用
f1=(sum(X1.*[W(1);W(2);W(6);W(9)],1)+sum(X2.*[W(3:5)';W(7:8)';W(10:12)'],1))';
f2=(sum(X3.*C([1,2,6,9])',1)+sum(X4.*C([3,4,5,7,8,10,11,12])',1))';
F=sum(f1)+sum(f2);

function J=jianyan3(X,b,WPCR,A_x,B_x,C_x,D_x)
%检验变量参与运算后是否出现小于0的值，是则不满足条件
X=X';
nn=2;
KC_WPCR=zeros(1,length(WPCR)+nn);%记录每天WPCR库存
KC=zeros(3,length(WPCR)+nn);%记录每天ABC库存
KC_x=zeros(8,length(WPCR)+nn);%记录每天ABC小件库存
SY_WPCR=zeros(1,length(WPCR)+nn);%记录每天交付WPCR情况
SY=zeros(3,length(WPCR)+nn);%记录每天使用ABC情况
SY_x=zeros(8,length(WPCR)+nn);%记录每天使用ABC小件情况
SC_WPCR=zeros(1,length(WPCR)+nn);%记录每天组装WPCR情况
SC=zeros(3,length(WPCR)+nn);%记录每天生产ABC情况
SC_x=zeros(8,length(WPCR)+nn);%记录每天生产ABC小件情况
for i=1:length(WPCR)%循环遍历每个WPCR
    x=X(i,2:4);
    %更新SC、KC、SY矩阵
    %生产
    if length(find(b==i))==1
        SC_WPCR(i+nn)=0;
    else
        SC_WPCR(i+nn)=X(i,1);
    end
    if length(find(b==i-1))==1
        SC(:,i+nn-1)=0;
    else
        SC(:,i+nn-1)=SC(:,i+nn-1)+x';
    end
    %放库存
    KC_WPCR(i+nn)=KC_WPCR(i+nn-1)+SC_WPCR(i+nn);
    if KC_WPCR(i+nn)<0
        KC_WPCR(i+nn)=0;
    end
    if i==1
        KC(:,i+nn-1)=SC(:,i+nn-1);
    else
        KC(:,i+nn-1)=KC(:,i+nn-1)+SC(:,i+nn-1);
    end
    KC_x(1:3,i+nn-2)=D_x(1:3).*SC(1,i+nn-1);
    KC_x(4:5,i+nn-2)=D_x(4:5).*SC(2,i+nn-1);
    KC_x(6:8,i+nn-2)=D_x(6:8).*SC(3,i+nn-1);
    %使用
    SY_WPCR(i+nn)=WPCR(i);
    SY(:,i+nn)=[A_x;B_x;C_x].*SY_WPCR(i+nn);
    %更新库存
    KC_WPCR(i+nn)=KC_WPCR(i+nn)-WPCR(i);
    KC(:,i+nn)=KC(:,i+nn-1)-SY(:,i+nn);
end
if length(find(KC_WPCR<0))>0 | length(find(KC<0))>0 | length(find(KC_x<0))>0
    J=1;
else
    J=0;
end

5.4 问题四模型的建立与求解

5.4.1 数据分析与数据预处理

题目中给出的30周历史数据，经分析发现预测对象“未来某周的WPCR订单数”是按照时间序列排列起的，构成时间序列，从构成的这一组时间序列过去的变化规律，推断今后变化的可能性及其变化趋势、变化规律，可以选择建立时间序列预测模型。另外，观察30周201天的数据无缺失数据。定义以周为单位的时间变量，以时间为横轴，机器人数量为纵轴绘制时间序列图。分析时间序列图，发现数据在一定范围内上下波动，无趋势、呈现出相当程度的季节性（季节性指周一到周日有各自的数据特点）。

表 11 SPSS分析数据

季节因子
序列名称	周期	季节因子 (%)
VAR00010	1	100.9
	2	94.5
	3	102.7
	4	105.4
	5	99.5
	6	90.2
	7	106.8
WEEK, not periodic	1	104.3
	2	102.8
	3	101.4
	4	100.1
	5	98.6
	6	97.1
	7	95.8
DAY, period 7	1	25.0
	2	50.0
	3	75.0
	4	100.0
	5	125.0
	6	150.0
	7	175.0

因此，本文采取季节性序列进行预测未来某周的WPCR订单数。

5.4.2 基于一元时间季节性序列预测模型的建立与检验

训练组数据是为以7为周期长度的序列，利用SPSS专家建模器建立最优时间序列分析模型，选择简单季节性模型进行求解。

检验模型是否识别完全：估计完成时间序列模型后，本文对残差进行白噪声检验，如果残差是白噪声，则说明我们选取的模型能完全识别出时间序列谁的规律,即模型可接受；如果残差不是白噪声,说明还有部分信息没有被模型所识别,则剔除。

ACF自相关系数、PACF偏自相关函数可以帮助判断残差是否为白噪声，即该时间序列是否能被模型识别完全。

表 12 模型统计结果

从上表可以看出，对残差进行Q检验得到的p值为0.451，即我们无法拒绝原假设，认为残差就是白噪声序列，因此简单季节性模型能够很好的识别本题中的机器人使用需求数据。

BIC(贝叶斯信息准则)表达式如下：

                                                                 

得出结果如下：

表 13 WPCR预测订单量

天	WPCR预测订单数量
周一	39
周二	35
周三	39
周四	41
周五	38
周六	33
周日	40

5.4.3 约束条件

约束一：保障每天正常交付

为保障每天的机器人订单均已95%以上的概率交付，因此对机器人组装数量的约束条件进行修改，如下所示：

                                                    

约束二：保障整周正常交付

为保障整周的机器人订单均能以85% 以上的概率交付，因此作出如下约束：

                                      

值得注意的是，每天的订单均已95%以上的概率交付，则整周的机器人订单必定均能以85%以上的概率交付，即（24）式已暗含于(23）式。因此保证每天正常交付即可，即可以不考虑（24）式。

5.4.4 问题四求解

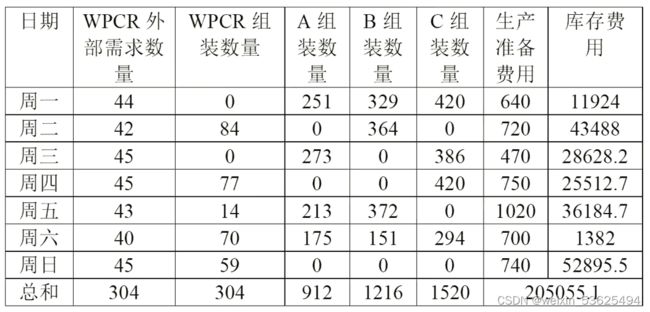
将上述条件，带入基于问题二的模型中进行求解，得到结果如下表所示：

表 14 问题四的结果数据

日期	WPCR外部需求数量	WPCR组装数量	A组装数量	B组装数量	C组装数量	生产准备费用	库存费用
周一	39	0	249	333	415	390	32108
周二	35	83	0	0	475	870	30481
周三	39	0	285	379	0	160	2012.5
周四	41	95	0	0	0	520	8969
周五	38	0	0	308	0	500	40508
周六	33	0	231	0	385	180	1578.5
周日	40	77	0	0	0	980	52513
总和	265	255	765	1020	1275	171770

给出其他物件的组装量和剩余量

表 17 小组件的组装数据

A1 组装数量	A2组装数量	A3组装数量	B1 组装数量	B2 组装数量	C1 组装数量	C2 组装数量	C3 组装数量
0	0	0	0	0	3800	950	5700
1710	2280	570	758	1516	0	0	0
0	0	0	0	0	0	0	0
0	0	0	616	1232	0	0	0
1386	1848	462	0	0	3080	770	4620
0	0	0	0	0	0	0	0
1494	1992	498	666	1332	3320	830	4980
4590	6120	1530	2040	4080	10200	2550	15300

表 18 各组件的剩余量

WPCR 剩余数量	A 剩余数量	B 剩余数量	C 剩余数量	A1 剩余数量	A2 剩余数量	A3 剩余数量	B1 剩余数量	B2 剩余数量	C1 剩余数量	C2 剩余数量	C3 剩余数量
0	249	333	415	0	0	0	0	0	3800	950	5700
83	0	0	475	1710	2280	570	758	1516	0	0	0
0	285	379	0	0	0	0	0	0	0	0	0
95	0	0	0	0	0	0	616	1232	0	0	0
0	0	308	0	1386	1848	462	0	0	3080	770	4620
0	231	0	385	0	0	0	0	0	0	0	0
77	0	0	0	1494	1992	498	666	1332	3320	830	4980
255	765	1020	1275	4590	6120	1530	2040	4080	10200	2550	15300

6、模型的优缺点

问题一、问题二和问题四都选择了基于Lingo软件的线性规划模型进行求解，所得结果相较于模拟退火等优化算法，有着更为准确的结果，不会出现将局部最优解作为全局最优解作为最终生产计划。但是该算法总时间复杂度来说比模拟退火等算法更为庞大，运算时间成为该模型的一个不可忽略的弊端。

正是由于基于Lingo软件的线性规划模型时间复杂度随着变量的增多而呈指数式增长。所以在解决第三问时，本小组刚开始仍然选择继续沿用问题一和问题二的模型，但是由于问题三的变量个数几乎已经达到了104的数量级，在用该模型时时间复杂度过大，在完成本论文时，已经运行了20余小时，运行过程见下图：

所以，在第三问时选择使用模拟退火算法进行解算，模拟退火算法优点在于时间复杂度小，解算速度快，但是容易陷入局部最优解，所以本文问题三求解出的解存在不是最优解的可能。

问题一标准答案

问题二标准答案

问题三标准答案 

 问题四标准答案