深度学习笔记----不同卷积类型的总结

目录

1，标准卷积

1.1  Same卷积

1.2 Valid卷积

1.3 Full卷积

 2,反卷积

3,空洞卷积（带孔卷积）

4.可变形卷积 

5，非局部卷积

5.1 非局部卷积介绍

5.2  Non-local block的结构

6，深度可分离卷积

7，组卷积

---

1，标准卷积

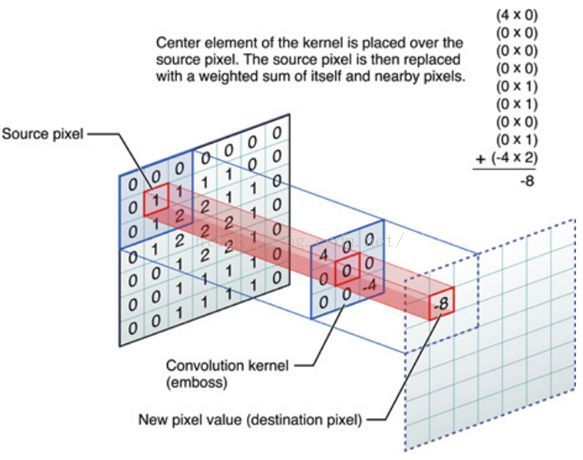
      卷积核上所有作用点依次作用于原始像素点后（即乘起来），线性叠加的输出结果，即是最终卷积的输出，也是我们想要的结果，我们称为destination（目标） pixel.

 标准卷积的计算公式为：

标准卷积有多种卷积方法，可划分为三种：Same卷积、Valid卷积、Full卷积(反卷积)。

有个博文详细讲卷积，可以参考下：

卷积原理_abyss_miracle的博客-CSDN博客_卷积原理

1.1  Same卷积

       通过Padding填充0运算保证卷积前后特征图大小不变，即W1=W2、H1=H2。公式为：(W1-K+2P)/S+1 = W2

      若令W1=W2则可计算填充0的P的值为多少。如，令K=3，S=1，W1=5，则计算P=1.

 1.2 Valid卷积

    不加入Padding运算，直接进行卷积运算，特征图会变小。公式为：(W1-K)/S+1=W2

    如，令W1=5，K=3，S=1，则W2=3

1.3 Full卷积

      实现full运算的核心步骤是在特征图中padding 0，然后进行卷积运算使得特征图变大。公式为：(W1-K+2P)/S+1 = W2

      如，令W1=5，K=3，P=2，S=1，则W2=7

 2,反卷积

     比较典型的就是 FCN结构使用的卷积方法， 反卷积运算方式则不同于以上的Full卷积方式，而是首先对特征图各神经元之间进行0填充，即上池化；然后再进行卷积运算。

计算公式为：(W1​−1)×S+K-2×P=W2

        通常卷积会造成分辨率降低，反卷积是卷积的逆向过程，就如卷积将4*4的变为2*2，反卷积的作用就是将2*2通过反卷积的作用，转换为4*4；

3,空洞卷积（带孔卷积）

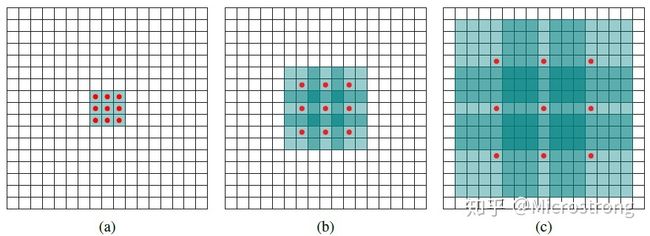
     标准的卷积操作中，卷积核的元素之间都是相邻的。但是，在空洞卷积中，卷积核的元素是间隔的，间隔的大小取决于空洞率。 如下图所示使用卷积核大小为3*3、空洞率（dilated rate）为2、卷积步长为1的空洞卷积操作对输入为7*7的特征图进行卷积生成3*3的特征图，如图2所示。

       下图中显示了正常卷积和空洞率为2和4的卷积。图(a)是正常卷积，（b）是空洞率为2的空洞卷积，（c）是空洞率为4的空洞卷积，可以看出，（b），（c）的感受野为别是7*7和15*15明显得到了提升。空洞卷积的作用就是再不增加计算量的同时，增加了模型的感受野，对图像分割任务中获取上下文的信息非常有用。

 空洞卷积的计算相关公式：

感受野尺寸=2（rate-1）*（K-1）+K  #K是kernel size 

例如，核是3*3的，空洞率是2，则感受野=2*（2-1）*（3-1）+3=7

带有空洞卷积的feature size的计算 

Output=(W-K+2P)/S+1  #w是上层feature的size，K是kernel size，S是stride

4.可变形卷积 

      卷积本身的操作是非常固定的几何形状，标准的卷积操作是一个非常规矩的采样。通常是正方形的，如果卷积采用非规矩的采样，形状不在是标准的正方形，而是任意形状这样的卷积核称为可变形卷积，如下图所示：

        图中展示了卷积核大小为 3x3 的正常卷积和可变形卷积的采样方式，(a) 所示的正常卷积规律的采样 9 个点（绿点），(b)(c)(d) 为可变形卷积，在正常的采样坐标上加上一个位移量（蓝色箭头），其中(c)(d) 作为 (b) 的特殊情况，展示了可变形卷积可以作为尺度变换，比例变换和旋转变换的特殊情况。

       由此可见，可变形卷积，不仅包含了权重系数还需要每个点的偏移量。举例说明，例如一个简单的3*3的卷积，可变形卷积仅仅做平移变换，就会包含18个偏移量系数（X.Y方向各9个偏移系量）。

       当通道共享偏移系数的时候。偏移系数和通道数无关，对于输入是M通道，输出时N通道，核为3*3的核来说，由于通道权重共享，所以权重 的参数是M*N*3*3,偏移参数是2*3*3，因此权重的参数远远大于偏移参数。而在后续的改进使用中，每个通道不在共享偏移量，其偏移量的参数变为2*3*3*M,但该参数量依旧比权重参数少，所以依旧不会大幅度增加模型的大小。且在实际应用中可以使用对通道组的分组共享偏移参数来降低参数。

     可变形卷积具有更加灵活的感受野，如下图所示：展示了两层结构，拥有标准固定感受野的卷积层 (a) 与拥有自适应感受野的可变性卷积层(b)。最上方是两个在不同大小的物体上的激活单元，中间是该单元所需的采样位置，最下方是中间的采样点分别所需的采样位置

     事实上，可变形卷积单元中增加的偏移量是网络结构的一部分，通过另外一个平行的标准卷积单元计算得到，进而也可以通过梯度反向传播进行端到端的学习。加上该偏移量的学习之后，可变形卷积核的大小和位置可以根据当前需要识别的图像内容进行动态调整，其直观效果就是不同位置的卷积核采样点位置会根据图像内容发生自适应的变化，从而适应不同物体的形状、大小等几何形变。下图展示了可变形卷积框架，首先通过一个小卷积层（绿色）的输出得到可变形卷积所需要的位移量，然后将其作用在卷积核（蓝色）上，达到可变形卷积的效果。

可变形卷积带来的好处：

1，增加了网络的空间变形适应性，对复杂的任务效果提升明显；

2，不增加额外的标注信息和训练代价，依旧使用原来的数据进行训练，并且可以同时训练卷积系数和偏移量，学习过程比较简单。对于增加的参数，可以通过分组进行控制；

5，非局部卷积

    在传统的CNN、DNN模型中，卷积层的计算只是将周围的特征加权加和，且一般当前层的计算只依赖前一层的结果，而现在的网络又大多使用1×1、3×3尺寸的小卷积核，对长距离相关特征的提取不足。 空洞卷积和可变形卷积都增加了感受野，但是增加的幅度都是有限的。有没有办法能够使卷积核的感受野是全图呢？非局部卷积就是用来实现这个目标。

5.1 非局部卷积介绍

     非局部（ Non-local）卷积，来自经典的非局部均值滤波算法，滤波后的值是输入值的的一个K,L邻域内的值的加权平均值。非局部（ Non-local）卷积将这个想法扩展到了全部的图像，图像上的任意一点都对中心像素的滤波结果有影响。

     非局部卷积（non-local convolution）由CMU和Facebook提出[4]。最初是用来处理视频图像分类任务中捕捉远距离像素之间的依赖关系的。传统的网络一般通过多次重复卷积操作来增加感受野，以捕捉远距离像素之间的依赖关系，但具有计算效率低、优化困难等问题。非局部卷积将一个位置处的响应表示为输入特征图中各个位置的特征的加权平均。如下图所示，其中  xi处的响应是该帧图像及相邻几帧图像所有像素处特征的加权平均。

5.2  Non-local block的结构

        Non-local是“CV注意力”的开篇之作，借鉴了传统CV领域的Non-local means滤镜算法，在特征图的每一个点上通过衡量与其他点的全局相关关系，来突出重点信息以优化分类效果。  非局部卷积可以应用于图像空间，也可以应用于不同时间帧，它可以通过维度变换来实现。下图显示了 Non-local 块的结构。

      如上图所示，先将输入的特征图降维（降到1维）后逐次嵌入（embed）到 theta、phi 和 g 三个向量中。然后，将向量 theta 和向量 phi 的转置相乘，做 softmax 激活后再与向量 g 相乘。最后，再将这个 Non-local 操作包裹一层，这通过一个1×1的卷积核和一个跨层连接实现残差结构。这样输入的维度和输出的维度是一样的，所以可以轻松的嵌入到任何卷积模块中。对于视频分类采用非局部卷积比对应的局部卷积网络效果要好，这是因为视频中的主体空间移动速度非常快，需要更大的感受野来捕捉信息。

6，深度可分离卷积

       Depthwise Separable Convolution是将一个完整的卷积运算分解为两步进行，即Depthwise Convolution与Pointwise Convolution。 

         Depthwise(DW)卷积与Pointwise(PW)卷积，合起来被称作Depthwise Separable Convolution(参见Google的Xception)，该结构和常规卷积操作类似，可用来提取特征，但相比于常规卷积操作，其参数量和运算成本较低。所以在一些轻量级网络中会碰到这种结构如MobileNet。

        Depthwise Convolution的一个卷积核负责一个通道，一个通道只被一个卷积核卷积。

       Pointwise Convolution的运算与常规卷积运算非常相似，它的卷积核的尺寸为 1×1×M，M为上一层的通道数。所以这里的卷积运算会将上一步的map在深度方向上进行加权组合，生成新的Feature map。有几个卷积核就有几个输出Feature map。如下图所示。

简而言之，

Depthwise ：就是在depth上面做文章，就是常说的channel ,对不同的channel使用不同的卷积核卷积提取特征

Pointwise：就是正常的卷积方式啦，但是是point的，就是对某一点，某一像素，所以kernel=[1,1]

        使用DW卷积后输出特征矩阵的channel是与输入特征矩阵的channel相等的，如果想改变/自定义输出特征矩阵的channel，那只需要在DW卷积后接上一个PW卷积即可。 下图是深度可分离卷积的完整过程。

 7，组卷积

      组卷积是把输入特征图在通道方向分成若干组，对每一组的特征分别做卷积后再拼接起来，以减少参数数量，提高运算速度。该方法在AlexNet中就被用来将特征图分解成两部分以分别部署到两个GPU上来处理内存消耗的问题。depthwise separable convolution可视作一种特殊的组卷积，使每一个分组只包含一个通道。

         组卷积可视作一种稀疏卷积连接的方式，即每一个输出通道只与输入通道中的某一个组相连，可能会丢失全局通道的信息。为了克服这个问题，微软推出了一种交错式组卷积（interleaved group convolutions，使输出通道能与所有输入通道相连。

       交错式组卷积如上图所示。假设输入由LM个通道，这里L = 2, M = 3。先将输入通道分成L个组，每个组包含M个通道，使用组卷积后将通道重新排序，分成M个组，每个组包含L个通道，再次进行组卷积。得到的输出即可捕捉到每个输入通道中的信息。