SGU 101.Domino (欧拉路)
时间限制: 0.5 sec
空间限制: 4096 KB
描述
多米诺骨牌,一种用小的方的木块或其他材料,每个都被一些点在面上标记,这些木块通常被称为骨牌。每个骨牌的面都被一条线分成两个 方形,两边各有一定点数。
N个多米诺骨牌,每个骨牌左右两侧分别有一个0~6的整数(骨牌可以旋转以调换其左右两数),
求一种把这些骨牌从左到右排列的方案,使得所有相邻的两数字相等(即左边骨牌右侧的数字等于右边骨牌左侧的数字)。
输入
第一行是一个整数N(1 ≤ N ≤ 100),表示骨牌的数量。接下来的N行描述每块骨牌,每块左右两边有不同的点数。
输出
如果无法安排,输出“No solution”。如果可能,输出任何一种,每行有一个数字,和“+”或“-”,前者代表不旋转,后者代表旋转。
样例输入
5
1 2
2 4
2 4
6 4
2 1
样例输出
2 -
5 +
1 +
3 +
4 -
{================================}
分析:
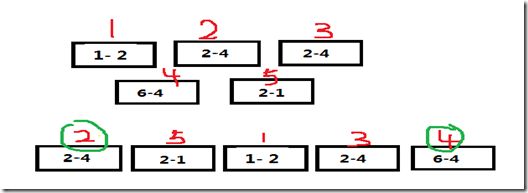
要对牌进行排序,上图对应样例,红色标记的是牌的编号,绿色圈出来的是需要翻转的牌。
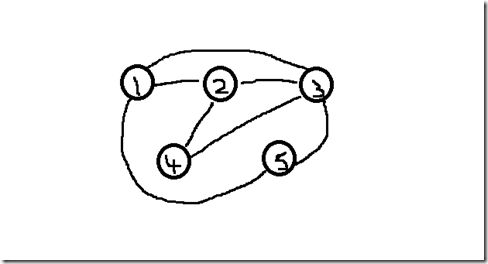
如果把每一张牌当做一个节点,有相同数字的两张牌之间连接一条边,如下图
那么只需要找到一条路径经过所有节点,并且只经过每个节点一次。即一个图的哈密顿路径
找到一个图的哈密顿路径的时间复杂度的是O(n^2),而判断哈密顿路径的存在却是NP完全问题,而题目的时限只有0.5s,显然不能满足我们的要求.是否有更好的方法呢?
我们换种方式建图:
考虑:把每个数字当做一个节点,每张牌当做一条边。
如图
那么现在的目标是找到一条路径,经过每一条边且只经过一次,即图的欧拉路
题中最多有0~6,7个节点,100条边,如果使用朴素的DFS的话,还是会超时,这时要充分运用欧拉路的性质进行剪枝
(1)无向欧拉图度为奇的节点数为0或2;
(2)欧拉图从奇度节点出发,如果没有任意一个偶度节点都能行;
经过测试,如果构图时使用链式前向星,枚举边进行DFS还是会在较大的数据上超时
所以还需要进一步优化
枚举顶点,如果两个节点之间有多条边的话,可以进行边的剪枝,
如果a,b两点有多条边,从节点a搜到节点b时,不能从b节点找到符合条件的路径
那么这时a和b其他的边也可以不搜了,直接搜下一个对顶点 例如 a和c。
由于最多只有7个顶点,21个点对。这样时间上便非常充裕了。
参考代码:(后面有更优的fleury算法)
#include <cstdio>
#include <vector>
#include <cmath>
using namespace std;
const int INF = 211;
//Edge记录点对间边的编号
vector<int> Edge[7][7];
int eSum[7], Path[INF], pd[INF];
int n, x, y;
int Find (int x, int cur) {
if (cur == n) return 1;
for (int i = 0; i <= 6; i++){
for (int j = 0; j < Edge[x][i].size(); j++) {
int num = (int) abs (Edge[x][i][j]);
if (pd[num] == 0) {
//Path保存路径,pd[]标记边的使用情况
Path[cur] = Edge[x][i][j], pd[num] = 1;
if (Find (i, cur + 1) ) return 1;
pd[num] = 0; break;
}
}
}
return 0;
}
int main() {
scanf ("%d", &n);
for (int i = 1; i <= n; i++) {
scanf ("%d %d", &x, &y);
//正负号记录使用的是正边还是反边
eSum[x]++, Edge[x][y].push_back (i);
eSum[y]++, Edge[y][x].push_back (-i);
}
x = 0, y = 0;
//x记录奇度节点个数
for (int i = 0; i <= 6; i++) if (eSum[i] & 1) x++;
if (x == 0 || x == 2) {
for (int i = 0; i <= 6; i++) {
//去掉不符合要求的起点
if (eSum[i] == 0) continue;
if (x == 2 && (eSum[i] & 1) == 0) continue;
if (Find (i, 0) ) break;
//如果有解,那么符合要求的任意起点都能找到解
//所以只需一次Find()即可
puts ("No solution");
return 0;
}
for (int i = 0; i <= n - 1; i++)
printf ("%d %c\n", (int) abs (Path[i]), Path[i] < 0 ? '-' : '+');
}
else
puts ("No solution");
return 0;
}
一个多月之前并不知道欧拉路的fleury算法,用了DFS加剪枝优化,SGU上代码运行的时间为32ms。
在了解了欧拉路O(m)的算法后,又把这道题重写了一遍,时间为15ms,内存也从246kb减少了到110kb。
code
#include <iostream>
#include <cstdio>
using namespace std;
struct node {
int v, ne, sta, id;
} edge[210];
int deg[7], head[7], cnt = 1, ans[210][2], vis[210], tol;
int n, m, x, y;
//链式前向星存边
void addedge (int u, int v, int id, int sta) {
edge[++cnt].v = v; edge[cnt].id = id;
edge[cnt].ne = head[u], edge[cnt].sta = sta;
head[u] = cnt;
}
void EulerianP (int x) {
for (int i = head[x]; i != 0; i = edge[i].ne) {
int v = edge[i].v, p = edge[i].id, sta = edge[i].sta;
if (!vis[i]) {
//标记走过的边,不再删除标记!
vis[i] = vis[i ^ 1] = 1;
EulerianP (v);
ans[++tol][0] = p;
ans[tol][1] = sta;
}
}
}
int main() {
scanf ("%d", &n);
for (int i = 1; i <= n; i++) {
scanf ("%d %d", &x, &y);
deg[x]++, deg[y]++;
addedge (x, y, i, 1);//正向边记为1
addedge (y, x, i, 0);//反向边记为0
}
int sum = 0, s = -1;
//统计奇度点
for (int i = 0; i <= 6; i++)
if (deg[i] & 1) sum++, s = i;
if (sum != 0 && sum != 2) {
puts ("No solution");
return 0;
}
if (s != -1) EulerianP (s);
else//寻找起点
for (int i = 0; i <= 6; i++)
if (deg[i] > 0) {
EulerianP (i);
break;
}
if (tol != n) {
puts ("No solution");
return 0;
}
for (int i = n; i >= 1; i--)
printf ("%d %c\n", ans[i][0], ans[i][1] == 1 ? '+' : '-');
return 0;
}
http://www.cnblogs.com/keam37/ keam所有 转载请注明出处