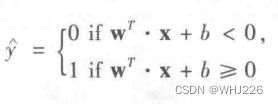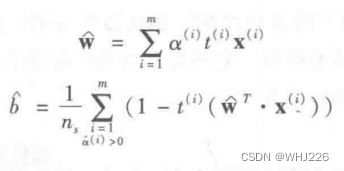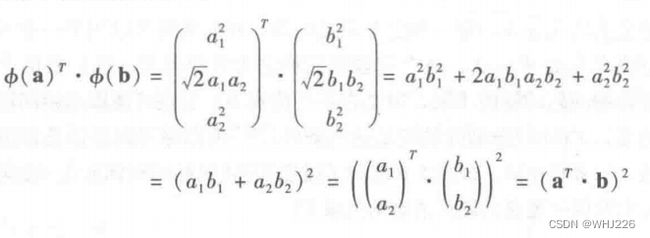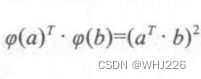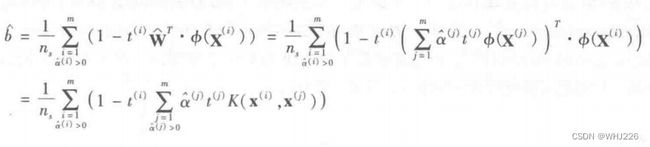机器学习实战（5）——支持向量机

目录

1 线性SVM分类

2 软间隔分类

3 非线性SVM分类

4 多项式核

5 添加相似特征

6 高斯RBF核函数

7 SVM回归

8 工作原理

8.1 决策函数和预测

8.2 训练目标

8.3 二次规划

8.4 对偶问题

8.5 核化SVM

---

支持向量机（简称SVM）是一个功能强大并且全面的机器学习模型，它能够执行线性或非线性分类、回归、甚至是异常值检测任务。SVM特别适用于中小型复杂数据集的分类。本篇博文中理论和理解的东西特别多。实在不懂的可以去哔哩哔哩找浙江大学胡浩基老师讲的支持向量机，简单易懂。（机器学习课程（六）支持向量机（线性模型）问题【720P】.qsv.flv_哔哩哔哩_bilibili）

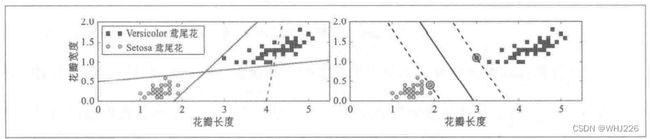
1 线性SVM分类

大间隔分类

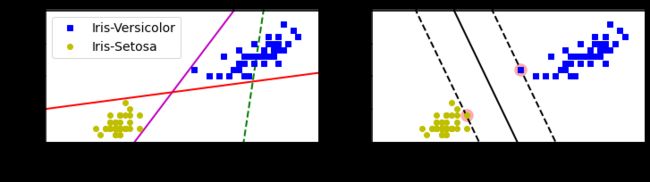
上图所示的数据集来自鸢尾花数据集的一部分。左图显示了三种可能的线性分类器的决策边界。其中虚线所代表的的模型表现非常糟糕，甚至都无法正确实现分类其余两个模型在这个训练集上表现良好，但是他们的决策边界与实例过于接近，导致在面对新实例时，表现可能不太会好。相比之下，右图中的实现代表SVM分类器的决策边界，这条线不仅分离了两个类别，并且尽可能远离了最近的训练实例。我们可以将SVM分类器视为在类别之间拟合可能的最宽的街道（平行的虚线）。因此这也叫做大间隔分类。（位于街道边缘的实例称为支持向量）

大间隔分类代码演示：

常规模块的导入以及图像可视化的设置：

# Common imports
import numpy as np
import os

# to make this notebook's output stable across runs
np.random.seed(42) #结果复现

# To plot pretty figures #可视化
%matplotlib inline
import matplotlib as mpl
import matplotlib.pyplot as plt
mpl.rc('axes', labelsize=14)
mpl.rc('xtick', labelsize=12)
mpl.rc('ytick', labelsize=12)

from sklearn.svm import SVC
from sklearn import datasets

iris = datasets.load_iris() #加载数据
X = iris["data"][:, (2, 3)]  # 花瓣长度和宽度
y = iris["target"]

setosa_or_versicolor = (y == 0) | (y == 1)
X = X[setosa_or_versicolor]
y = y[setosa_or_versicolor]

# SVM Classifier model
svm_clf = SVC(kernel="linear", C=float("inf"))
svm_clf.fit(X, y)

# Bad models
x0 = np.linspace(0, 5.5, 200)
pred_1 = 5*x0 - 20
pred_2 = x0 - 1.8
pred_3 = 0.1 * x0 + 0.5

def plot_svc_decision_boundary(svm_clf, xmin, xmax):
    w = svm_clf.coef_[0]
    b = svm_clf.intercept_[0]

    # At the decision boundary, w0*x0 + w1*x1 + b = 0
    # => x1 = -w0/w1 * x0 - b/w1
    x0 = np.linspace(xmin, xmax, 200)
    decision_boundary = -w[0]/w[1] * x0 - b/w[1]

    margin = 1/w[1]
    gutter_up = decision_boundary + margin
    gutter_down = decision_boundary - margin

    svs = svm_clf.support_vectors_
    plt.scatter(svs[:, 0], svs[:, 1], s=180, facecolors='#FFAAAA')
    plt.plot(x0, decision_boundary, "k-", linewidth=2)
    plt.plot(x0, gutter_up, "k--", linewidth=2)
    plt.plot(x0, gutter_down, "k--", linewidth=2)

plt.figure(figsize=(12,2.7))

plt.subplot(121)
plt.plot(x0, pred_1, "g--", linewidth=2)
plt.plot(x0, pred_2, "m-", linewidth=2)
plt.plot(x0, pred_3, "r-", linewidth=2)
plt.plot(X[:, 0][y==1], X[:, 1][y==1], "bs", label="Iris-Versicolor")
plt.plot(X[:, 0][y==0], X[:, 1][y==0], "yo", label="Iris-Setosa")
plt.xlabel("Petal length", fontsize=14)
plt.ylabel("Petal width", fontsize=14)
plt.legend(loc="upper left", fontsize=14)
plt.axis([0, 5.5, 0, 2])

plt.subplot(122)
plot_svc_decision_boundary(svm_clf, 0, 5.5)
plt.plot(X[:, 0][y==1], X[:, 1][y==1], "bs")
plt.plot(X[:, 0][y==0], X[:, 1][y==0], "yo")
plt.xlabel("Petal length", fontsize=14)
plt.axis([0, 5.5, 0, 2])

plt.show()

运行结果如下：

大间隔分类

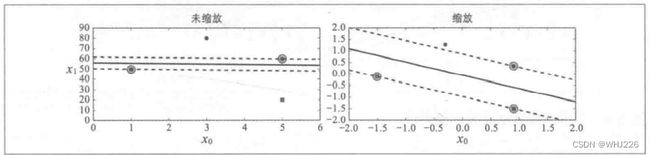
注意：SVM对特征缩放非常敏感，如下图，在左图中，垂直刻度比水平刻度大得多，因此可能的最宽的街道接近于水平。在特征缩放后，决策边界看起来好很多（右图）。

对特征缩放的敏感度

Xs = np.array([[1, 50], [5, 20], [3, 80], [5, 60]]).astype(np.float64)
ys = np.array([0, 0, 1, 1])
svm_clf = SVC(kernel="linear", C=100)
svm_clf.fit(Xs, ys)

plt.figure(figsize=(12,3.2))
plt.subplot(121)
plt.plot(Xs[:, 0][ys==1], Xs[:, 1][ys==1], "bo")
plt.plot(Xs[:, 0][ys==0], Xs[:, 1][ys==0], "ms")
plot_svc_decision_boundary(svm_clf, 0, 6)
plt.xlabel("$x_0$", fontsize=20)
plt.ylabel("$x_1$  ", fontsize=20, rotation=0)
plt.title("Unscaled", fontsize=16)
plt.axis([0, 6, 0, 90])

from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
X_scaled = scaler.fit_transform(Xs)
svm_clf.fit(X_scaled, ys)

plt.subplot(122)
plt.plot(X_scaled[:, 0][ys==1], X_scaled[:, 1][ys==1], "bo")
plt.plot(X_scaled[:, 0][ys==0], X_scaled[:, 1][ys==0], "ms")
plot_svc_decision_boundary(svm_clf, -2, 2)
plt.xlabel("$x_0$", fontsize=20)
plt.title("Scaled", fontsize=16)
plt.axis([-2, 2, -2, 2])

 运行结果如下：

对特征缩放的敏感度

2 软间隔分类

如果我们严格地让所有实例都不在街道上，并且位于正确的一边，这就是硬间隔分类。硬间隔分类有两个主要问题。首先，它只在数据是线性可分离的时候才有效；其次，它对异常值非常敏感。下图显示了有一个额外异常值的鸢尾花数据：左图的数据根本找不到硬间隔，而右图最终显示的决策边界与我们大间隔分类图中所看到的无异常值时的决策边界也大不相同，可能无法更好地泛化。

硬间隔对异常值的敏感度

X_outliers = np.array([[3.4, 1.3], [3.2, 0.8]])
y_outliers = np.array([0, 0])
Xo1 = np.concatenate([X, X_outliers[:1]], axis=0)
yo1 = np.concatenate([y, y_outliers[:1]], axis=0)
Xo2 = np.concatenate([X, X_outliers[1:]], axis=0)
yo2 = np.concatenate([y, y_outliers[1:]], axis=0)

svm_clf2 = SVC(kernel="linear", C=10**9)
svm_clf2.fit(Xo2, yo2)

plt.figure(figsize=(12,2.7))

plt.subplot(121)
plt.plot(Xo1[:, 0][yo1==1], Xo1[:, 1][yo1==1], "bs")
plt.plot(Xo1[:, 0][yo1==0], Xo1[:, 1][yo1==0], "yo")
plt.text(0.3, 1.0, "Impossible!", fontsize=24, color="red")
plt.xlabel("Petal length", fontsize=14)
plt.ylabel("Petal width", fontsize=14)
plt.annotate("Outlier",
             xy=(X_outliers[0][0], X_outliers[0][1]),
             xytext=(2.5, 1.7),
             ha="center",
             arrowprops=dict(facecolor='black', shrink=0.1),
             fontsize=16,
            )
plt.axis([0, 5.5, 0, 2])

plt.subplot(122)
plt.plot(Xo2[:, 0][yo2==1], Xo2[:, 1][yo2==1], "bs")
plt.plot(Xo2[:, 0][yo2==0], Xo2[:, 1][yo2==0], "yo")
plot_svc_decision_boundary(svm_clf2, 0, 5.5)
plt.xlabel("Petal length", fontsize=14)
plt.annotate("Outlier",
             xy=(X_outliers[1][0], X_outliers[1][1]),
             xytext=(3.2, 0.08),
             ha="center",
             arrowprops=dict(facecolor='black', shrink=0.1),
             fontsize=16,
            )
plt.axis([0, 5.5, 0, 2])

plt.show()

运行结果如下：

硬间隔对异常值的敏感度

那么怎么避免这些问题？尽可能在保持街道宽阔和限制间隔违例（即位于街道之上，甚至是错误一边的实例）之间找到良好的平衡，这就是软间隔。

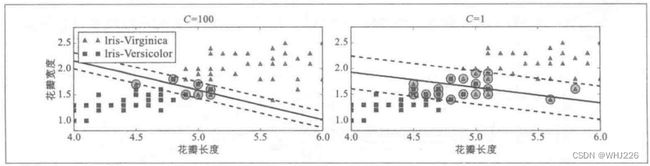
在Scikit-Learn的SVM分类中，我们可以通过超参数C来控制这个平衡：C值越小，则街道越宽，但是间隔违例也会越来越多。下图显示了在一个非线性可分类数据集上，两个软间隔SVM分类器各自的决策边界和间隔。左边使用了高C值，分类器的间隔违例较少，但是间隔也较小。右边使用了低C值，间隔大了很多，但是位于街道上的实例也更多。但是第二个分类器的泛化效果更好，因为大多数间隔违例实际上都位于决策边界正确的一边，所以即便是在该训练集上，他做出的错误预测也会更少。

较小间隔违例和大间隔对比

如果SVM模型过度拟合，可以试试通过降低C来进行正则化。

 代码实现：

import numpy as np
from sklearn import datasets
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.svm import LinearSVC

iris = datasets.load_iris()
X = iris["data"][:, (2, 3)]  # petal length, petal width
y = (iris["target"] == 2).astype(np.float64)  # Iris-Virginica

svm_clf = Pipeline([
        ("scaler", StandardScaler()),
        ("linear_svc", LinearSVC(C=1, loss="hinge", random_state=42)),
    ])

svm_clf.fit(X, y)



scaler = StandardScaler()
svm_clf1 = LinearSVC(C=1, loss="hinge", random_state=42)
svm_clf2 = LinearSVC(C=100, loss="hinge", random_state=42)

scaled_svm_clf1 = Pipeline([
        ("scaler", scaler),
        ("linear_svc", svm_clf1),
    ])
scaled_svm_clf2 = Pipeline([
        ("scaler", scaler),
        ("linear_svc", svm_clf2),
    ])

scaled_svm_clf1.fit(X, y)
scaled_svm_clf2.fit(X, y)


# Convert to unscaled parameters
b1 = svm_clf1.decision_function([-scaler.mean_ / scaler.scale_])
b2 = svm_clf2.decision_function([-scaler.mean_ / scaler.scale_])
w1 = svm_clf1.coef_[0] / scaler.scale_
w2 = svm_clf2.coef_[0] / scaler.scale_
svm_clf1.intercept_ = np.array([b1])
svm_clf2.intercept_ = np.array([b2])
svm_clf1.coef_ = np.array([w1])
svm_clf2.coef_ = np.array([w2])

# Find support vectors (LinearSVC does not do this automatically)
t = y * 2 - 1
support_vectors_idx1 = (t * (X.dot(w1) + b1) < 1).ravel()
support_vectors_idx2 = (t * (X.dot(w2) + b2) < 1).ravel()
svm_clf1.support_vectors_ = X[support_vectors_idx1]
svm_clf2.support_vectors_ = X[support_vectors_idx2]


plt.figure(figsize=(12,3.2))
plt.subplot(121)
plt.plot(X[:, 0][y==1], X[:, 1][y==1], "g^", label="Iris-Virginica")
plt.plot(X[:, 0][y==0], X[:, 1][y==0], "bs", label="Iris-Versicolor")
plot_svc_decision_boundary(svm_clf1, 4, 6)
plt.xlabel("Petal length", fontsize=14)
plt.ylabel("Petal width", fontsize=14)
plt.legend(loc="upper left", fontsize=14)
plt.title("$C = {}$".format(svm_clf1.C), fontsize=16)
plt.axis([4, 6, 0.8, 2.8])

plt.subplot(122)
plt.plot(X[:, 0][y==1], X[:, 1][y==1], "g^")
plt.plot(X[:, 0][y==0], X[:, 1][y==0], "bs")
plot_svc_decision_boundary(svm_clf2, 4, 6)
plt.xlabel("Petal length", fontsize=14)
plt.title("$C = {}$".format(svm_clf2.C), fontsize=16)
plt.axis([4, 6, 0.8, 2.8])

运行结果如下：

较小间隔违例和大间隔对比

 我们可以用模型做出预测：

svm_clf.predict([[5.5, 1.7]])

运行结果如下：

array([1.])

与Logistic回归分类器不同的是，SVM分类器不会输出每个类别的概率。

LinearSVC类会对偏置项进行正则化，所以需要我们先减去平均值，使训练集集中。如果使用StandScaler会自动进行这一步。另外，需要确保超参数loss设置为“hinge”，因为它不是默认值，为了获得更好的性能，还应该将超参数dual设置为False。

3 非线性SVM分类

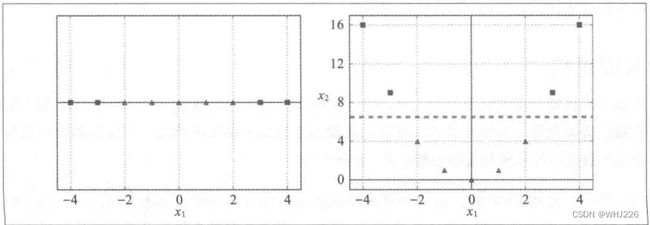
处理非线性数据集的方法之一是添加更多特征，比如多项式特征，这可能导致数据集变得线性可分离。如下图：左图是一个简单的数据集，只有一个特征，数据集线性不可分；但是我们添加第二个特征，生成的数据集则线性可分离。

通过添加特征使数据集线性可分离

 代码实现：

X1D = np.linspace(-4, 4, 9).reshape(-1, 1)
X2D = np.c_[X1D, X1D**2]
y = np.array([0, 0, 1, 1, 1, 1, 1, 0, 0])

plt.figure(figsize=(11, 4))

plt.subplot(121)
plt.grid(True, which='both')
plt.axhline(y=0, color='k')
plt.plot(X1D[:, 0][y==0], np.zeros(4), "bs")
plt.plot(X1D[:, 0][y==1], np.zeros(5), "g^")
plt.gca().get_yaxis().set_ticks([])
plt.xlabel(r"$x_1$", fontsize=20)
plt.axis([-4.5, 4.5, -0.2, 0.2])

plt.subplot(122)
plt.grid(True, which='both')
plt.axhline(y=0, color='k')
plt.axvline(x=0, color='k')
plt.plot(X2D[:, 0][y==0], X2D[:, 1][y==0], "bs")
plt.plot(X2D[:, 0][y==1], X2D[:, 1][y==1], "g^")
plt.xlabel(r"$x_1$", fontsize=20)
plt.ylabel(r"$x_2$", fontsize=20, rotation=0)
plt.gca().get_yaxis().set_ticks([0, 4, 8, 12, 16])
plt.plot([-4.5, 4.5], [6.5, 6.5], "r--", linewidth=3)
plt.axis([-4.5, 4.5, -1, 17])

plt.subplots_adjust(right=1)

plt.show()

运行结果如下：

通过添加特征使数据集线性可分离

使用Scikit-Learn实现这个想法，可以搭建一条流水线：一个PolynomialFeatures 转换器，接着一个StandardScaler，然后是LinearSVC。

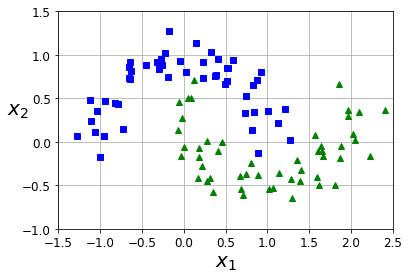
我们用卫星数据集来进行测试：

加载数据并可视化：

from sklearn.datasets import make_moons
X, y = make_moons(n_samples=100, noise=0.15, random_state=42)

def plot_dataset(X, y, axes):
    plt.plot(X[:, 0][y==0], X[:, 1][y==0], "bs") #标签y==0的数据点
    plt.plot(X[:, 0][y==1], X[:, 1][y==1], "g^") #标签y==1的数据点
    plt.axis(axes)
    plt.grid(True, which='both')
    plt.xlabel(r"$x_1$", fontsize=20)
    plt.ylabel(r"$x_2$", fontsize=20, rotation=0)

plot_dataset(X, y, [-1.5, 2.5, -1, 1.5])
plt.show()

运行结果如下：

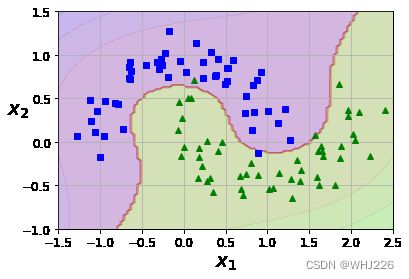
接着测试：

from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures

polynomial_svm_clf = Pipeline([
        ("poly_features", PolynomialFeatures(degree=3)),
        ("scaler", StandardScaler()),
        ("svm_clf", LinearSVC(C=10, loss="hinge", random_state=42))
    ])

polynomial_svm_clf.fit(X, y)

def plot_predictions(clf, axes):
    x0s = np.linspace(axes[0], axes[1], 100)
    x1s = np.linspace(axes[2], axes[3], 100)
    x0, x1 = np.meshgrid(x0s, x1s)
    X = np.c_[x0.ravel(), x1.ravel()]
    y_pred = clf.predict(X).reshape(x0.shape)
    y_decision = clf.decision_function(X).reshape(x0.shape)
    plt.contourf(x0, x1, y_pred, cmap=plt.cm.brg, alpha=0.2)
    plt.contourf(x0, x1, y_decision, cmap=plt.cm.brg, alpha=0.1)

plot_predictions(polynomial_svm_clf, [-1.5, 2.5, -1, 1.5])
plot_dataset(X, y, [-1.5, 2.5, -1, 1.5])

plt.show()

运行结果如下：

4 多项式核

问题是，如果多项式太低阶，处理不了非常复杂的数据集，而高阶会创造出大量的特征，导致模型变得太慢。不过，使用SVC时，通过应用特殊的数学技巧（核技巧），它产生的结果就跟添加了许多多项式特征，甚至是非常高阶的多项式特征一样，但实际上并不需要真的添加。因为实际没有添加任何特征，所以就不存在数量爆炸的组合特征了。

我们在卫星数据集上进行测试：

首先使用一个3阶多项式内核训练SVC分类器：

from sklearn.svm import SVC

poly_kernel_svm_clf = Pipeline([
        ("scaler", StandardScaler()),
        ("svm_clf", SVC(kernel="poly", degree=3, coef0=1, C=5))
    ])
poly_kernel_svm_clf.fit(X, y)

其次使用一个10阶多项式内核训练SVC分类器：

poly100_kernel_svm_clf = Pipeline([
        ("scaler", StandardScaler()),
        ("svm_clf", SVC(kernel="poly", degree=10, coef0=100, C=5))
    ])
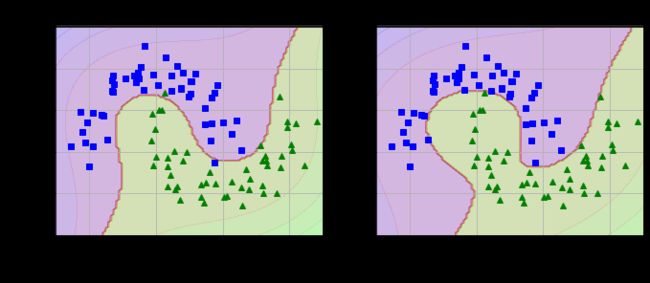
poly100_kernel_svm_clf.fit(X, y)

可视化：

plt.figure(figsize=(11, 4))

plt.subplot(121)
plot_predictions(poly_kernel_svm_clf, [-1.5, 2.5, -1, 1.5])
plot_dataset(X, y, [-1.5, 2.5, -1, 1.5])
plt.title(r"$d=3, r=1, C=5$", fontsize=18)

plt.subplot(122)
plot_predictions(poly100_kernel_svm_clf, [-1.5, 2.5, -1, 1.5])
plot_dataset(X, y, [-1.5, 2.5, -1, 1.5])
plt.title(r"$d=10, r=100, C=5$", fontsize=18)

plt.show()

运行结果如下：

从结果来看，如果模型过度拟合，我们可以降低多项式阶数，如果模型拟合不足，我们需要提升阶数。其中超参数coefo控制的是模型受高阶多项式还是低阶多项式影响的程度。

5 添加相似特征

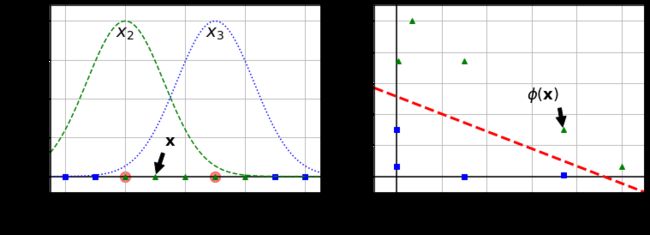
解决非线性问题的另一种技术是添加相似特征。这些特征经过相似函数计算得出，相似函数可以测量每个实例与一个特定地标之间的相似度。如下图。（添加地标最简单的方法是在数据集里每一个实例的位置上创建一个地标。这会创造出许多维度，因而也增加了转换后的训练集线性可分离的机会）

如左图，在x1=-2和x1=1处添加两个地标。下面，我们采用高斯径向基函数（RBF）作为相似函数，=0.3。

现在我们计算新特征， 例如，我们看到实例x1=-1 ：它与第一个地标距离为1，与第二个地标距离为2。因此新特征为， ，转化后的数据集如右图（去除了原始特征），现在我们可以看到数据是线性可分离的了。

代码实现如下：

def gaussian_rbf(x, landmark, gamma):
    return np.exp(-gamma * np.linalg.norm(x - landmark, axis=1)**2)

gamma = 0.3

x1s = np.linspace(-4.5, 4.5, 200).reshape(-1, 1)
x2s = gaussian_rbf(x1s, -2, gamma)
x3s = gaussian_rbf(x1s, 1, gamma)

XK = np.c_[gaussian_rbf(X1D, -2, gamma), gaussian_rbf(X1D, 1, gamma)]
yk = np.array([0, 0, 1, 1, 1, 1, 1, 0, 0])

plt.figure(figsize=(11, 4))

plt.subplot(121)
plt.grid(True, which='both')
plt.axhline(y=0, color='k')
plt.scatter(x=[-2, 1], y=[0, 0], s=150, alpha=0.5, c="red")
plt.plot(X1D[:, 0][yk==0], np.zeros(4), "bs")
plt.plot(X1D[:, 0][yk==1], np.zeros(5), "g^")
plt.plot(x1s, x2s, "g--")
plt.plot(x1s, x3s, "b:")
plt.gca().get_yaxis().set_ticks([0, 0.25, 0.5, 0.75, 1])
plt.xlabel(r"$x_1$", fontsize=20)
plt.ylabel(r"Similarity", fontsize=14)
plt.annotate(r'$\mathbf{x}$',
             xy=(X1D[3, 0], 0),
             xytext=(-0.5, 0.20),
             ha="center",
             arrowprops=dict(facecolor='black', shrink=0.1),
             fontsize=18,
            )
plt.text(-2, 0.9, "$x_2$", ha="center", fontsize=20)
plt.text(1, 0.9, "$x_3$", ha="center", fontsize=20)
plt.axis([-4.5, 4.5, -0.1, 1.1])

plt.subplot(122)
plt.grid(True, which='both')
plt.axhline(y=0, color='k')
plt.axvline(x=0, color='k')
plt.plot(XK[:, 0][yk==0], XK[:, 1][yk==0], "bs")
plt.plot(XK[:, 0][yk==1], XK[:, 1][yk==1], "g^")
plt.xlabel(r"$x_2$", fontsize=20)
plt.ylabel(r"$x_3$  ", fontsize=20, rotation=0)
plt.annotate(r'$\phi\left(\mathbf{x}\right)$',
             xy=(XK[3, 0], XK[3, 1]),
             xytext=(0.65, 0.50),
             ha="center",
             arrowprops=dict(facecolor='black', shrink=0.1),
             fontsize=18,
            )
plt.plot([-0.1, 1.1], [0.57, -0.1], "r--", linewidth=3)
plt.axis([-0.1, 1.1, -0.1, 1.1])
    
plt.subplots_adjust(right=1)

plt.show()

运行结果如下：

  

x1_example = X1D[3, 0]
for landmark in (-2, 1):
    k = gaussian_rbf(np.array([[x1_example]]), np.array([[landmark]]), gamma)
    print("Phi({}, {}) = {}".format(x1_example, landmark, k))

运行结果如下：

Phi(-1.0, -2) = [0.74081822]
Phi(-1.0, 1) = [0.30119421]
​

6 高斯RBF核函数

我们使用SVC类试试高斯RBF核：

rbf_kernel_svm_clf = Pipeline([
        ("scaler", StandardScaler()),
        ("svm_clf", SVC(kernel="rbf", gamma=5, C=0.001))
    ])
rbf_kernel_svm_clf.fit(X, y)


#可视化
from sklearn.svm import SVC

gamma1, gamma2 = 0.1, 5
C1, C2 = 0.001, 1000
hyperparams = (gamma1, C1), (gamma1, C2), (gamma2, C1), (gamma2, C2)

svm_clfs = []
for gamma, C in hyperparams:
    rbf_kernel_svm_clf = Pipeline([
            ("scaler", StandardScaler()),
            ("svm_clf", SVC(kernel="rbf", gamma=gamma, C=C))
        ])
    rbf_kernel_svm_clf.fit(X, y)
    svm_clfs.append(rbf_kernel_svm_clf)

plt.figure(figsize=(11, 7))

for i, svm_clf in enumerate(svm_clfs):
    plt.subplot(221 + i)
    plot_predictions(svm_clf, [-1.5, 2.5, -1, 1.5])
    plot_dataset(X, y, [-1.5, 2.5, -1, 1.5])
    gamma, C = hyperparams[i]
    plt.title(r"$\gamma = {}, C = {}$".format(gamma, C), fontsize=16)


plt.show()

运行结果如下：

增加gamma值会使钟形曲线变得更窄，每个实例的影响范围随之变小：决策边界变得更不规则，开始围绕单个实例转弯。减小gamma值使钟形曲线变得更宽，每个实例的影响范围随之增大，决策边界变得更平坦。（gamma类似于超参数）

注意：这么多核函数中，我们永远先从线性核函数开始尝试（LinearSVC比SVC(kernel="linear")快得多） 。

7 SVM回归

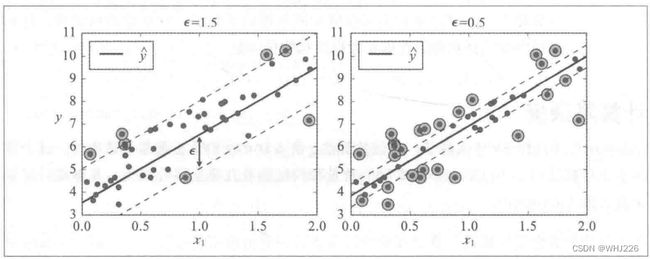
SVM算法非常全面：不仅支持线性和非线性分类，而且支持线性和非线性回归SVM。只需要将目标反转：不再是尝试拟合两个类别之间可能的最宽的街道的同时限制间隔违例，SVM回归要做的是让尽可能多的实例位于街道上，同时限制间隔违例（也就是不在街道上的实例）。街道的宽度有超参数  控制。下图显示了用随机线性数据训练的两个线性SVM回归模型，一个间隔较大，一个间隔较小。

在间隔内添加更多的实例不会影响模型的预测，所以这个模型被称为  不敏感。

我们可以使用Scikit-Learn的LinearSVR类来执行线性SVM回归。

代码如下：

np.random.seed(42)
m = 50
X = 2 * np.random.rand(m, 1)
y = (4 + 3 * X + np.random.randn(m, 1)).ravel()


from sklearn.svm import LinearSVR

svm_reg = LinearSVR(epsilon=1.5, random_state=42)
svm_reg.fit(X, y)


svm_reg1 = LinearSVR(epsilon=1.5, random_state=42)
svm_reg2 = LinearSVR(epsilon=0.5, random_state=42)
svm_reg1.fit(X, y)
svm_reg2.fit(X, y)

def find_support_vectors(svm_reg, X, y):
    y_pred = svm_reg.predict(X)
    off_margin = (np.abs(y - y_pred) >= svm_reg.epsilon)
    return np.argwhere(off_margin)

svm_reg1.support_ = find_support_vectors(svm_reg1, X, y)
svm_reg2.support_ = find_support_vectors(svm_reg2, X, y)

eps_x1 = 1
eps_y_pred = svm_reg1.predict([[eps_x1]])



def plot_svm_regression(svm_reg, X, y, axes):
    x1s = np.linspace(axes[0], axes[1], 100).reshape(100, 1)
    y_pred = svm_reg.predict(x1s)
    plt.plot(x1s, y_pred, "k-", linewidth=2, label=r"$\hat{y}$")
    plt.plot(x1s, y_pred + svm_reg.epsilon, "k--")
    plt.plot(x1s, y_pred - svm_reg.epsilon, "k--")
    plt.scatter(X[svm_reg.support_], y[svm_reg.support_], s=180, facecolors='#FFAAAA')
    plt.plot(X, y, "bo")
    plt.xlabel(r"$x_1$", fontsize=18)
    plt.legend(loc="upper left", fontsize=18)
    plt.axis(axes)

plt.figure(figsize=(9, 4))
plt.subplot(121)
plot_svm_regression(svm_reg1, X, y, [0, 2, 3, 11])
plt.title(r"$\epsilon = {}$".format(svm_reg1.epsilon), fontsize=18)
plt.ylabel(r"$y$", fontsize=18, rotation=0)
#plt.plot([eps_x1, eps_x1], [eps_y_pred, eps_y_pred - svm_reg1.epsilon], "k-", linewidth=2)
plt.annotate(
        '', xy=(eps_x1, eps_y_pred), xycoords='data',
        xytext=(eps_x1, eps_y_pred - svm_reg1.epsilon),
        textcoords='data', arrowprops={'arrowstyle': '<->', 'linewidth': 1.5}
    )
plt.text(0.91, 5.6, r"$\epsilon$", fontsize=20)
plt.subplot(122)
plot_svm_regression(svm_reg2, X, y, [0, 2, 3, 11])
plt.title(r"$\epsilon = {}$".format(svm_reg2.epsilon), fontsize=18)

plt.show()

运行结果如下：

解决非线性回归任务，可以使用核化的SVM模型。例如，下图显示了在一个随机二次训练集，使用二阶多项式核的SVM回归。左图几乎没有正则化（C值很大），右图则过度正则化。 

我们可以使用Scikit-Learn的SVR类（支持核技巧）。 SVR类是SVC类的回归等价物，LinearSVR类也是LinearSVC类的回归等价物。LinearSVR与训练集的大小线性相关（LinearSVC同），而SVR则在训练集变大时，变得很慢（SVC同）。

代码实现如下：

np.random.seed(42)
m = 100
X = 2 * np.random.rand(m, 1) - 1
y = (0.2 + 0.1 * X + 0.5 * X**2 + np.random.randn(m, 1)/10).ravel()


from sklearn.svm import SVR

svm_poly_reg = SVR(kernel="poly", degree=2, C=100, epsilon=0.1, gamma="auto")
svm_poly_reg.fit(X, y)



svm_poly_reg1 = SVR(kernel="poly", degree=2, C=100, epsilon=0.1, gamma="auto")
svm_poly_reg2 = SVR(kernel="poly", degree=2, C=0.01, epsilon=0.1, gamma="auto")
svm_poly_reg1.fit(X, y)
svm_poly_reg2.fit(X, y)



plt.figure(figsize=(9, 4))
plt.subplot(121)
plot_svm_regression(svm_poly_reg1, X, y, [-1, 1, 0, 1])
plt.title(r"$degree={}, C={}, \epsilon = {}$".format(svm_poly_reg1.degree, svm_poly_reg1.C, svm_poly_reg1.epsilon), fontsize=18)
plt.ylabel(r"$y$", fontsize=18, rotation=0)
plt.subplot(122)
plot_svm_regression(svm_poly_reg2, X, y, [-1, 1, 0, 1])
plt.title(r"$degree={}, C={}, \epsilon = {}$".format(svm_poly_reg2.degree, svm_poly_reg2.C, svm_poly_reg2.epsilon), fontsize=18)

plt.show()

运行结果如下：

8 工作原理

以下博文内容中我们去深入了解SVM的。这里我们使用一个约定，在处理SVM时它更为方便：偏置项表示为b，特征权重向量表示w，同时输入特征向量中不添加偏置特征。

8.1 决策函数和预测

线性SVM分类器通过简单地计算决策函数  来预测新实例x的分类。如果结果为正，则预测类别  是正类（1），反之负类（0）。

线性SVM分类器预测

下图显示了“较小间隔违例和大间隔对比” 图中较大间隔模型所对应的决策函数：数据集包含两个特征（花瓣宽度和长度），所以显示二维平面。决策边界是决策函数等于0的点的集合：它是两个平面的交集（图中加粗实线所示）。虚线表示决策函数等于1或-1的点：它们互相平行，并与决策边界的距离相等，从而形成间隔（街道）。

 

训练线性SVM分类器即意味着找到w和b的值，从而使这个间隔尽可能宽的同时，避免（硬间隔）或是限制（软间隔）间隔违例。

代码实现如下:

iris = datasets.load_iris()
X = iris["data"][:, (2, 3)]  # petal length, petal width
y = (iris["target"] == 2).astype(np.float64)  # Iris-Virginica


from mpl_toolkits.mplot3d import Axes3D

def plot_3D_decision_function(ax, w, b, x1_lim=[4, 6], x2_lim=[0.8, 2.8]):
    x1_in_bounds = (X[:, 0] > x1_lim[0]) & (X[:, 0] < x1_lim[1])
    X_crop = X[x1_in_bounds]
    y_crop = y[x1_in_bounds]
    x1s = np.linspace(x1_lim[0], x1_lim[1], 20)
    x2s = np.linspace(x2_lim[0], x2_lim[1], 20)
    x1, x2 = np.meshgrid(x1s, x2s)
    xs = np.c_[x1.ravel(), x2.ravel()]
    df = (xs.dot(w) + b).reshape(x1.shape)
    m = 1 / np.linalg.norm(w)
    boundary_x2s = -x1s*(w[0]/w[1])-b/w[1]
    margin_x2s_1 = -x1s*(w[0]/w[1])-(b-1)/w[1]
    margin_x2s_2 = -x1s*(w[0]/w[1])-(b+1)/w[1]
    ax.plot_surface(x1s, x2, np.zeros_like(x1),
                    color="b", alpha=0.2, cstride=100, rstride=100)
    ax.plot(x1s, boundary_x2s, 0, "k-", linewidth=2, label=r"$h=0$")
    ax.plot(x1s, margin_x2s_1, 0, "k--", linewidth=2, label=r"$h=\pm 1$")
    ax.plot(x1s, margin_x2s_2, 0, "k--", linewidth=2)
    ax.plot(X_crop[:, 0][y_crop==1], X_crop[:, 1][y_crop==1], 0, "g^")
    ax.plot_wireframe(x1, x2, df, alpha=0.3, color="k")
    ax.plot(X_crop[:, 0][y_crop==0], X_crop[:, 1][y_crop==0], 0, "bs")
    ax.axis(x1_lim + x2_lim)
    ax.text(4.5, 2.5, 3.8, "Decision function $h$", fontsize=15)
    ax.set_xlabel(r"Petal length", fontsize=15)
    ax.set_ylabel(r"Petal width", fontsize=15)
    ax.set_zlabel(r"$h = \mathbf{w}^T \mathbf{x} + b$", fontsize=18)
    ax.legend(loc="upper left", fontsize=16)

fig = plt.figure(figsize=(10, 10))
ax1 = fig.add_subplot(111, projection='3d')
plot_3D_decision_function(ax1, w=svm_clf2.coef_[0], b=svm_clf2.intercept_[0])

plt.show()

运行结果如下：

8.2 训练目标

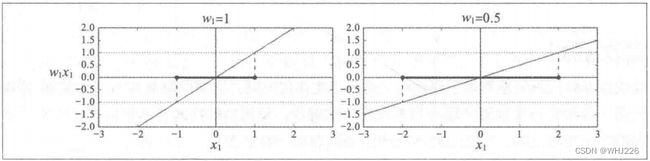
决策函数的斜率等于权重向量的范数，即  。如果我们将斜率除以2，那么决策函数等于  的点也将变得离决策函数两倍远。也就是说：权重向量w越小，间隔越大。

权重向量越小，间隔越大

 所以我们可以通过最小化  来得到尽可能大的间隔。但是，如果我们想避免任何间隔违例（硬间隔），那么就要使所有正类训练集的决策函数大于1，负类训练集的决策函数小于-1。如果我们定义，实例为负类（如果  ）时，；实例为正类（如果）时， 。那么我们可以将这个约束条件表示为：对所有实例来说， 。因此我们可以将硬间隔线性SVM分类器的目标，看做一个约束优化问题。

硬间隔线性SVM分类器的目标

注意：我们最小化的是  ，它等于  ，而不是最小化  。这是因为，虽然两者会得到相同的结果，但是  有一个简单好用的导数（W）。

要达到软间隔的目标，我们需要为每个实例引入一个松弛变量  ， 衡量的是第i个实例多大程度上允许间隔违例。那么我们现在有了两个互相冲突的目标：使松弛变量越小越好从而减少间隔违例，同时还要使   最小化以增大间隔。这正是超参数C的用武之地：允许我们在两个目标之间权衡。

软间隔线性SVM分类器的目标

8.3 二次规划

硬间隔和软间隔问题都属于线性约束的凸二次优化问题。这类问题被称为二次规划。

二次规划问题

注意表达式  实际上定义了  个约束：对于  ， ，其中  是包含A的第i行元素的向量，而  是b的第i个元素。

可以验证：如果我们把二次规划参数按以下方式设置，是否能够实现硬间隔线性SVM分类器的目标：

所以，要训练硬间隔线性SVM分类器，有一种办法是直接将上面的参数用在一个现成的二次规划求解器上。得到的向量p将会包括偏置项 ，以及特征权重  。类似地，我们也可以用二次规划求解器来解决软间隔问题。

8.4 对偶问题

针对一个给定的约束优化问题，称之为原始问题，或对偶问题（另一种表达）。通常来说，对偶问题的解只能算是原始问题的解的下限，但是在某些情况下，它也可能跟原始问题的解完全相同。SVM问题满足这些条件，所以我们可以选择是解决原始问题还是对偶问题，二者解相同。

线性SVM目标的对偶形式

一旦得到使得该等式最小化（使用二次规划求解器）的向量  ，就可以使用下面的公式计算原始问题最小化的  和  。

从对偶问题到原始问题

 

该公式用线性SVM分类器如何从对偶解走到原始解，但是如果我们应用了核技巧，最终得到的是包含  的方程。而  的维度数量必须与  相同，后者可能是无穷大的，我们可能无法计算。可是不知道  该如何做出预测，我们可以将该公式中  插入新实例  的决策函数中，这样就得到了一个只包含输入向量之间点积的公式，这时我们可以运用下面的核技巧。

  

8.5 核化SVM

如果你想要将一个二阶多项式转换为一个二维训练集，然后再转换训练集上训练训练线性SVM分类器。这个二阶多项式的映射函数如下所示：

二阶多项式映射

注意，转换后的向量是三维而不是二维的。如果我们应用这个二阶多项式映射，两个二维向量a和b会有什么变化， 然后再计算转换后两个向量的点击，如下：

二阶多项式映射的核技巧

转换后向量的点积等于原始向量的点积的平方：

如果将转换映射  应用于所有训练实例，那么对偶问题将包含点积  的计算。如果  是二阶多项式转换，那么可以直接用  来替代这个转换向量的点积。所以我们根本不需要转换训练实例，只需要将“线性SVM目标的对偶形式”中的点积换成点积的平方即可。

其中函数  被称为二阶多项式函数。机器学习中，核是能够仅基于原始向量a和b来计算点积  的函数，不需要计算转换函数  。以下是一些最常用的核函数。

常用核函数

使用核化SVM做出预测：

注意，因为仅对于支持向量才有  ，所以预测时，计算新输入向量  的点积，使用的仅仅是支持向量而不是全部训练实例，同时，需要使用同样的技巧来计算偏置项  。

使用核技巧计算偏置项：

学习笔记——《机器学习实战：基于Scikit-Learn和TensorFlow》