Leetcode各种题型题目+思路+代码(共176道题)
文章目录
- 第一章:Leetcode 每日很多题
-
- 1、Leetcode-1047 删除字符串中的所有相邻重复项
- 2、剑指 Offer 53 - I. 在排序数组中查找数字 I
- 3、Leetcode704:二分查找
- 4、 Leetcode 227:基本计算器II
- 5、leetcode 224:基本计算器(带括号的计算)
- 6、Leetcode 15:三数之和:排序+双指针
- 7、剑指 offer 38.字符串的排列
- 8、Leetcode409:最长回文串
- 9、Leetcode 331:验证二叉树的前序序列化
- 10、Leetcode 705:设计哈希集合
- 11、Leetcode 13:罗马数字转整数:
- 12、Leetcode 88:合并两个有序数组
- 13、Leetcode 706:设计哈希映射
- 14、Leetcode 54 螺旋矩阵:
- 15、 Leetcode 14 最长公共前缀
- 16、Leetcode 20:有效的括号
- 17、Leetcode 21:合并两个有序的链表
- 18、Leetcode 139:单词拆分问题
- 19、剑指Offer 29:顺时针打印矩阵
- 20、LCP 11: 期望个数统计
- 21、Leetcode 59:螺旋矩阵II
- 22、Leetcode 101 : 对称二叉树
- 23、Leetcode 115:不同的子序列
- 24、Leetcode 1603 :设计停车系统
- 25、Leetcode 290:单词规律
- 26、Leetcode 6:Z字形变换
- 27、Leetcode 914:卡牌分组
- 28、面试题 01.08 零矩阵:
- 29、Leetcode 150:逆波兰表达式求值
- 30、Leetcode 232:用栈实现队列
- 31、Leetcode 503:下一个更大元素II
- 32、Leetcode 131:分割回文串
- 33、Leetcode 92:反转链表II
- 第二章 二叉树/N叉树
-
- 1、Leetcode 94:二叉树的中序遍历
- 2、Leetcode 144:二叉树的前序遍历
- 3、Leetcode 145:二叉树的后序遍历
- 4、N叉树的后续遍历
- 5、Leetcode 589:N叉树的前序遍历:
- 6、Leetcode 429:N叉树的层序遍历
- 第三章:哈希表
-
- 1、Leetcode 242:有效的字母异位
- 2、 Leetcode 49:字母异位词分组
- 3、Leetcode1:两数之和
- 第四章 递归
-
- 1、 Leetcode-70: 爬楼梯问题
- 2、Leetcode-22:括号生成问题
- 3、Leetcode 98:验证二叉搜索树
- 4、Leetcode226:翻转二叉树
- 5、Leetcode104:二叉树的最大深度
- 6、Leetcode111:二叉树的最小深度
- 7、Leetcode509:斐波那契数列
- 8、Leetcode 297:二叉树的序列化和反序列化
- 9、Leetcode236:二叉树的公共祖先
- 10、Leetcode 105:从前序与中序遍历序列构造二叉树
- 11、 Leetcode 77: permutation
- 12、Leetcode 46:全排列
- 13、Leetcode 47:全排列II
- 第五章 动态规划
-
- 1、Leetcode 62:不同路径
- 2、Leetcode 63:不同路径II
- 3、Leetcode 1143:最长公共子序列
- 4、Leetcode 70:爬楼梯
- 5、Leetcode 120:三角形的最小路径和
- 6、Leetcode 55: 最大子序和
- 7、Leetcode 152:乘积最大子树和
- 8、Leetcode 332:零钱兑换问题
- 9、Leetcode 198:打家劫舍
- 10、Leetcode 121:买卖股票的最佳时机
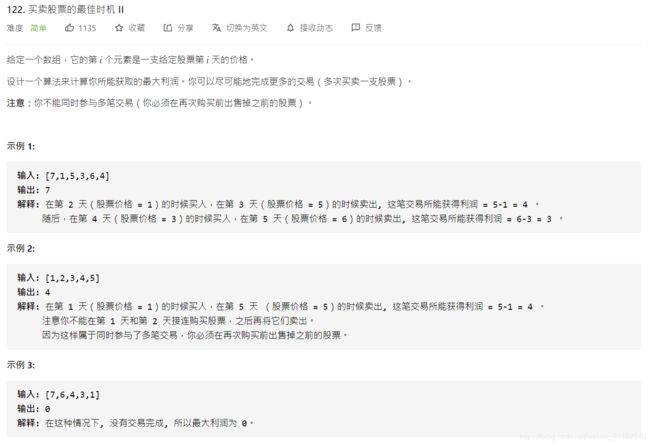
- 11、Leetcode 122:买入股票的最佳时机II
- 12、Leetcode 123:买卖股票的最佳时机III
- 13、Leetcode 309:最佳买卖股票时机含冷冻期
- 14、Leetcode 188:买卖股票的最佳时机IV
- 15、Leetcode 714:买卖股票的最佳时机含手续费
- 16、Leetcode 32:最长有效括号
- 17、Leetcode 64:最小路径和
- 18、Leetcode 72 :编辑距离
- 19、Leetcode 91:解码方法
- 20、Leetcode 221:最大正方形
- 21、Leetcode 403:青蛙过河
- 22、Leetcode 410:分割数组的最大值
- 23、Leetcode 552:学生出勤记录II
- 24、Leetcode 647:回文子串
- 25、Leetcode 76:最小覆盖子串
- 26、Leetcode 312:戳气球
- 27、Leetcode 213:打家劫舍ii
- 28、Leetcode 300:最长递增子序列
- 29、Leetcode 53:最大子序列和
- 30、Leetcode 72:编辑距离计算
- 31、Leetcode 332:零钱兑换
- 32、Leetcode 494:目标和
- 总结
- 第六章 分治、回溯
-
- 分治代码模板
- 回溯
- 1、Leetcode 50:Pow(x,n)
- 2、Leetcode 78:子集
- 3、Leetcode 169:多数元素
- 4、Leetcode 17:电话号码的字母组合
- 5、Leetcode 51:N皇后问题
- 第七章 深度优先搜索和广度优先搜索
-
- 1、Leetcode 102:二叉树的层序遍历
- 2、Leetcode 433:最小基因变化
- 3、Leetcode 22: 括号生成问题重写
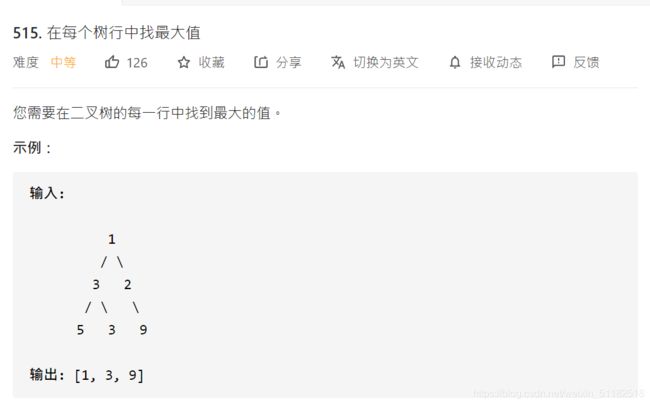
- 4、Leetcode 515:在每个树行中找最大值
- 5、Leetcode 127:单词接龙
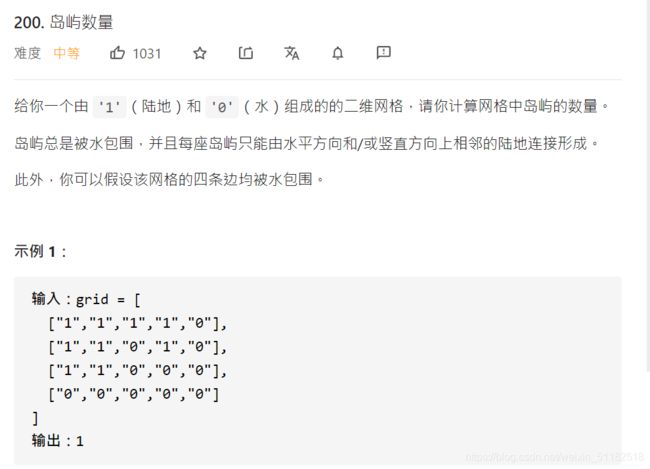
- 6、Leetcode 200:岛屿数量
- 第八章 :贪心搜索
-
- 1、Leetcode 455:分发饼干
- 2、Leetcode 122:买卖股票的最佳时机 II
- 3、Leetcode 55:跳跃游戏
- 4、Leetcode 860:柠檬水找零
- 5、Leetcode 874: 模拟行走机器人
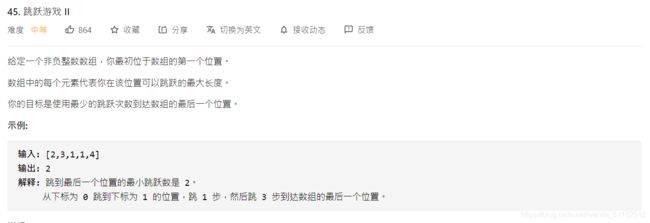
- 6、Leetcode 42: 跳跃游戏II
- 第九章 二分查找
-
- 1、Leetcode 69:x的平方根
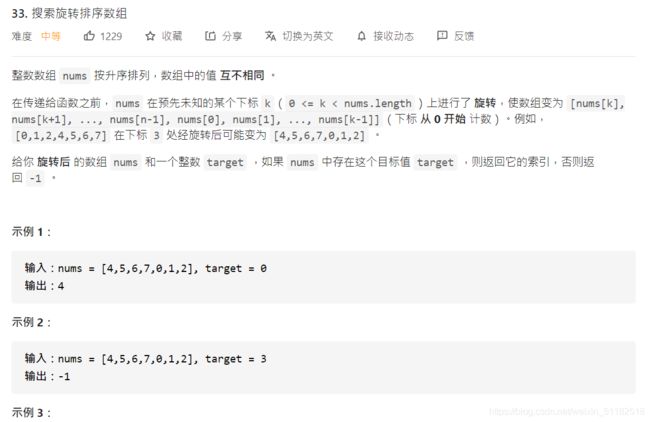
- 2、Leetcode 33:搜索旋转排序数组
- 3、Leetcode 367:有效的完全平方数
- 4、Leetcode 74:搜索二维矩阵
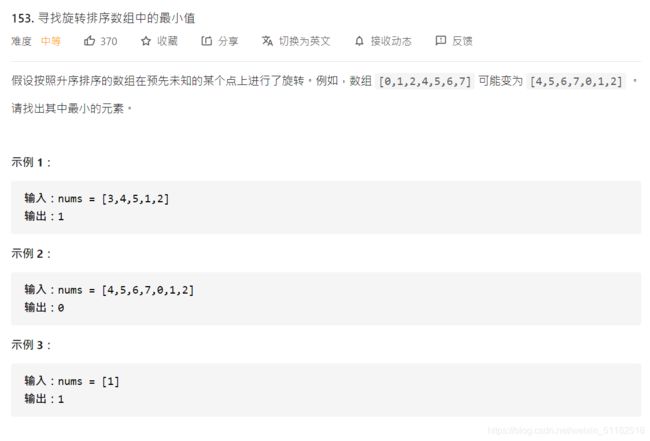
- 5、Leetcode 153:寻找旋转排序数组中的最小值
- 第十章 字典树
-
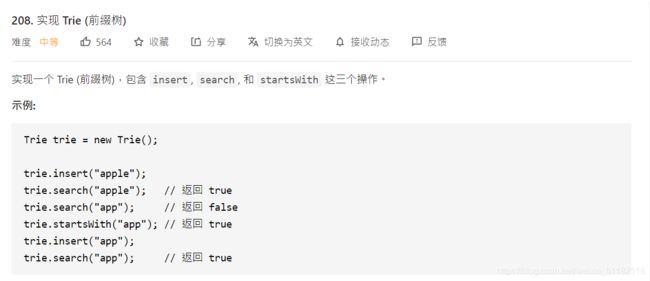
- 1、Leetcode 208:实现前缀树
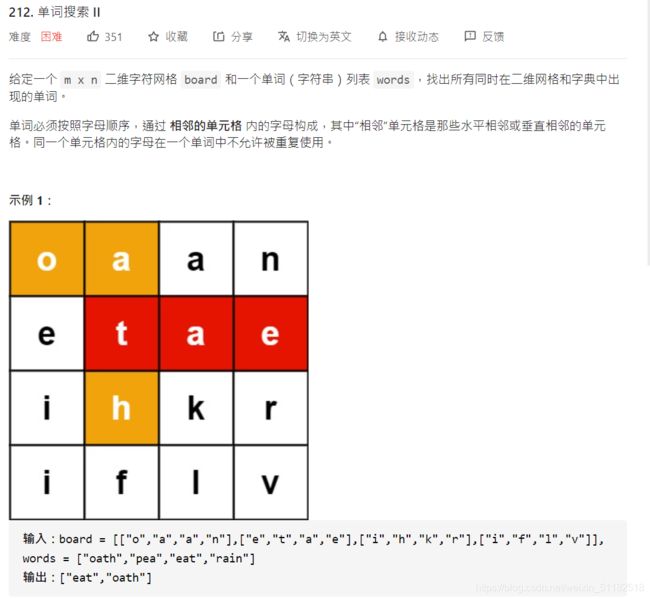
- 2、Leetcode 212:单词搜索
- 第十一章 并查集
-
- 1、Leetcode 200: 岛屿数量
- 2、Leetcode 130:被围绕的区域
- 第十二章 高级搜索
-
- 1、Leetcode 22 括号生成重新
- 2、Leetcode 51 :N皇后重写
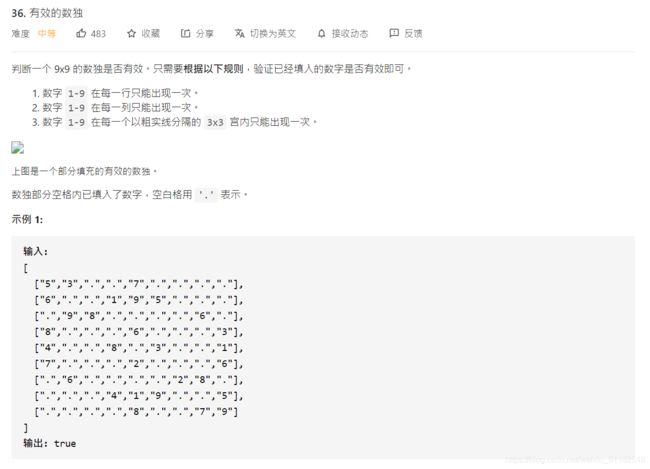
- 3、Leetcode 36:有效的数独
- 4、Leetcode 37:解数独
- 5、Leetcode 127:单词接龙重写
- 6、Leetcode 433:最小基因变化重新
- 7、Leetcode 773:滑动谜题
- 第十三章 红黑树和AVL树
- 第十四章 排序算法
-
- 1、简单的排序
-
- 冒泡排序
- 选择排序
- 插入排序
- 希尔排序
- 2、高级排序
-
- 快速排序
- 归并排序
- 3、Leetcode 1122:数组的相对排序
- 4、Leetcode 242:有效的字母异位词
- 5、Leetcode 1244:力扣排行榜
- 6、Leetcode 56:合并区间
- 7、剑指Offer 51 数组中的逆序对
- 8、Leetcode 491: 翻转对
- 第十五章 字符串相关问题
-
- 1、Leetcode 709 转换成小写字母
- 2、Leetcode 58:最后一个单词的长度
- 3、Leetcode 771:宝石与石头
- 4、剑指offer 50:第一个只出现一次的字符
- 5、Leetcode 8:字符串转换整数
- 6、Leetcode 14:最长公共前缀
- 7、Leetcode 344:反转字符串
- 8、Leetcode 541:反转字符串ii
- 9、Leetcode 151:反转字符串里的单词
- 10、Leetcode 557:反转字符串中的单词III
- 11、Leetcode 917:仅仅反转字母
- 12、Leetcode 242:有效的字母异位词重写
- 13、Leetcode 49:字母异位词分组:
- 14、Leetcode 438:找到字符串中的所有字母异位词
- 15、Leetcode 1143:最长公共子序列重写
- 16、Leetcode 125:验证回文串
- 17、Leetcode 680:验证回文字符串ii
- 18、Leetcode 5:最长回文子串
- 19、Leetcode 72:编辑距离重写
- 20、Leetcode 10:正则表达式匹配
- 21、Leetcode 44:通配符匹配
- 22、Leetcode 115:不同的子序列重写
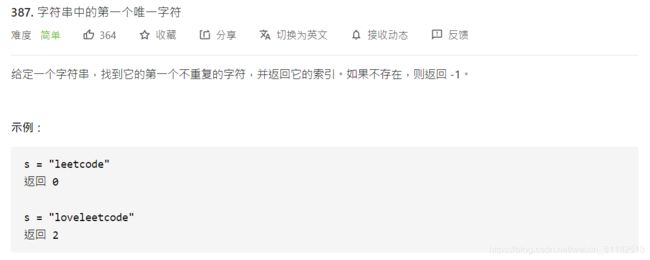
- 23、Leetcode 387:字符串中的第一个唯一字符
- 24、Leetcode 8:字符串转换整数重写
- 25、Leetcode 541:反转字符串II重写
- 26、Leetcode 151:翻转字符串里的单词重写
- 27、Leetcode 537:反转字符串中的单词iii重写
- 28、Leetcode 917:仅反转字母重写
- 29、Leetcode 438:找到字符串中所有字母异位词重写
- 30、Leetcode 5:最长回文串重写
- 31、Leetcode 205:同构字符串
- 32、Leetcode 680:验证回文字符串II重写
- 33、Leetcode 44:通配符匹配重写
- 34、Leetcode 32:最长有效括号重写
- 35、Leetcode 115:不同的子序列重写
- 第十六章 高级动态规划
-
- 1、Leetcode 300:最长递增子序列重做
- 2、Leetcode 91:解码方法重做
- 3、Leetcode 32:最长有效括号重写
- 4、Leetcode 85:最大矩形
- 5、Leetcode 115:不同的子序列重写
- 6、Leetcode 818:赛车
- 第十七章 布隆过滤器&LRU cache
-
- Leetcode 146:LRU缓存机制
- 第十八章 位运算
-
- 1、Leetcode 191:位1的个数
- 2、Leetcode 231:2的幂
- 3、 Leetcode 190:颠倒二进制位
- 4、Leetcode 51:N皇后问题的位运算解法
- 5、Leetcode 52:N皇后ii
- 6、Leetcode 338:比特位计数
第一章:Leetcode 每日很多题
1、Leetcode-1047 删除字符串中的所有相邻重复项
题目描述:

题目思路:
使用stack的思路,先把字符串的第一个字母压栈,然后判断下一个待压栈的字母是否与stack[-1]的字母相同,如果相同,该字母不进入stack中,且stack.pop()将重复的字母剔除。如此遍历一遍字符串,最后返回stack中的元素即为消除重复字后的字符串。
举例:"abbaca"
- 建立栈
- 把a压栈
- b与a不相同,压栈
- 第二个b和stack栈口元素相同,不要第二个b且把栈扣的b pop掉。
- 第四个元素:a,此时stack中还有一个元素a,相同,不要第四个元素且把stack中的a pop掉
- 压c,压a
- 返回ca即为结果
代码:
def main(S):
stack=[]
for i in S:
if stack and stack[-1]==i:
stack.pop()
else:
stack.append(i)
return "".join(stack)
2、剑指 Offer 53 - I. 在排序数组中查找数字 I
代码实现
class Solution:
def search(self, nums: List[int], target: int) -> int:
dic1=collections.defaultdict(int)
for i in nums:
dic1[i]+=1
return dic1[target] if dic1[target] else 0
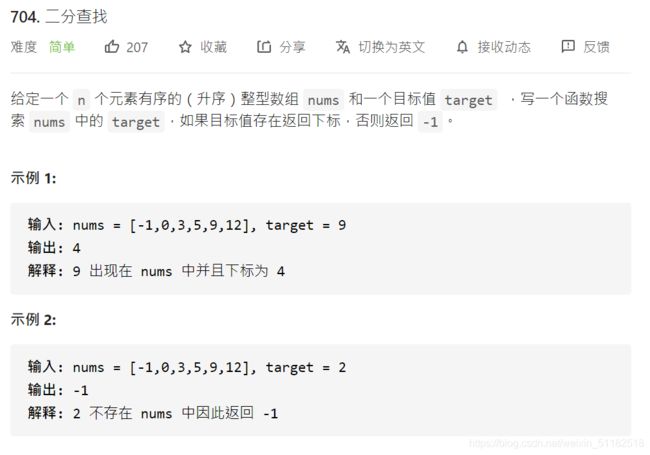
3、Leetcode704:二分查找
class Solution:
def search(self, nums: List[int], target: int) -> int:
left=0
right=len(nums)-1
while left<=right:
mid=(left+right)//2
if nums[mid]>target:
right=mid-1
elif nums[mid]<target:
left=mid+1
else:
return mid
return -1
4、 Leetcode 227:基本计算器II
题目描述:

解题思路:
首先对于计算器来说有加减乘除四种符号,对于加减的符号,运算主要看加减符号后面的两个数字。对于乘除符号,运算主要看乘除符号前后的数字。解题思路是维护一个栈,遍历输入字符串,当遇到的都是数字那么把它们做累加定义为变量num,当遍历到不是数字时,空格的话忽略。如果是计算符号,在当前时刻查看上一个符号,会有四种情况:
- “+”:只需把num的数字压栈即可
- “-”:只需把num的相反数压栈即可
- “*”:需要从栈中取出上一次压栈的数字并与当前num做乘法压栈。
- “/”:需要把栈中上一次压栈的数字并与当前num做除法取整即可。
对于出现计算符号的每个时刻计算的都是它前面保留的num和上一次符号的计算。所以当前时刻计算压栈后,prev_flag定义为当前符号,在下一次出现计算符号开始计算,num作为计数变量也要清零。
代码
class Solution:
def calculate(self, s: str) -> int:
s+="$"
stack=[]
pre_flag="+"
num=0
for i in s:
if i.isdigit():
num=num*10+int(i)
elif i==" ":
continue
else:
if pre_flag=="+":
stack.append(num)
elif pre_flag=="-":
stack.append(-(num))
elif pre_flag=="*":
stack.append(stack.pop()*num)
elif pre_flag=="/":
stack.append(int(stack.pop()/num))
pre_flag=i
num=0
return sum(stack)
5、leetcode 224:基本计算器(带括号的计算)
解题思路:
与第九题大致相同,但加入一个递归去计算每次括号中的数字,并且返回,如此递归下去。
class Solution:
def calculate(self, s: str) -> int:
def dfs(s,start):
stack=[]
prev_flag="+"
i=start
num=0
while i <len(s):
if s[i]==" ":
i+=1
continue
elif s[i].isdigit():
num=num*10+int(s[i])
elif s[i]=="(":
i,num=dfs(s,i+1)
else:
if prev_flag=="+":
stack.append(num)
elif prev_flag=="-":
stack.append(-num)
if s[i]==")":
break
prev_flag=s[i]
num=0
i+=1
return i,sum(stack)
s+="$"
return dfs(s,0)[1]
6、Leetcode 15:三数之和:排序+双指针
解题思路:
首先面对三树之和,先将列表用sort进行排序,然后第一层遍历每一个元素,对于每一次每一个位置的元素,都设定左右指针,右指针指list最后,左指针为当前元素的下一个。即:
- left=i+1
- right=len(list)-1
接下来就是一个判别式,具体为三种情况: - 如果左右指针对应元素小于target-list[i],说明最小的不够大,left指针加1
- 如果左右指针对应元素大于target-list[i],说明最大的不够小,right指针减1
- 如果左右指针对应元素相加正好等于target-list[i],满足题意,把三个数存储在列表排序经过tuple后添加到res集合中。左右指针分别加1减1继续查看。
- 最后只要把res列表化就可以了
两个问题:
- 第一个问题是为了达到去重的效果我是把列表sorted后tuple化添加到集合中的,然后再把集合list,其实里面的还是tuple,但是在leetcode中输出的还是list of list的形式。不太明白这段怎么处理。
- 常见的三数之和也可以使用哈希表加两层for循环查找,但在之前的题目中,我是通过字典存储nums中每个元素是否出现,然后两层for 循环查找是否target-j-k是否在字典中。但该题中列表元素中有重复的,那么使用哈希表就还要存储它在nums中的index,这点没有想到办法处理。只能使用排序+双指针好理解一些。后续的处理是建立一个新列表,遍历集合中的元组列表化插入新的列表。这样就不需要判断和上一次枚举的不同的这个条件了。
代码
class Solution:
def threeSum(self, nums: List[int]) -> List[List[int]]:
nums.sort()
res=set()
for i in range(len(nums)):
j=i+1
k=len(nums)-1
while j <k:
if nums[j]+nums[k]<-nums[i]:
j+=1
elif nums[j]+nums[k]>-nums[i]:
k-=1
else:
res.add(tuple(sorted([nums[j],nums[k],nums[i]])))
k-=1
j+=1
list1=[]
for j in res:
list1.append(list(j))
return list1
7、剑指 offer 38.字符串的排列
问题描述
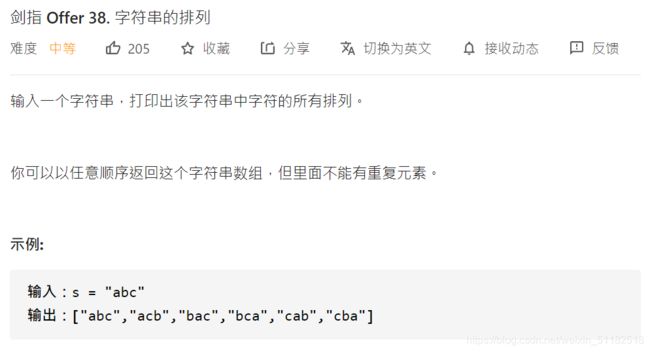
解题思路
最直接的办法就是对于一个给定字符串,对于第一个位置可以是任何字符串中的任何一个字母,分类讨论,固定好第一个字母,从剩下的字母中选择去固定下一个字母位置,如此递归,终止条件即位len-1的位置也固定好了以后,返回每一种情况。在其中要注意的是,如果列表中出现重复的字母的话,使用set()去重后,不需要让重复的再进行固定了。
代码
class Solution:
def permutation(self, s: str) -> List[str]:
c,res=list(s),[]
def dfs(x):
#终止条件:
if x==len(s)-1:
res.append("".join(c))
return
dic=set()
#循环字符串的每一个位置
for i in range(x,len(c)):
if c[i] in dic:#重复的不需要固定
continue
dic.add(c[i])
c[i],c[x]=c[x],c[i]
dfs(x+1)#对下一位进行递归
c[i],c[x]=c[x],c[i]#调换回来
dfs(0)
return res
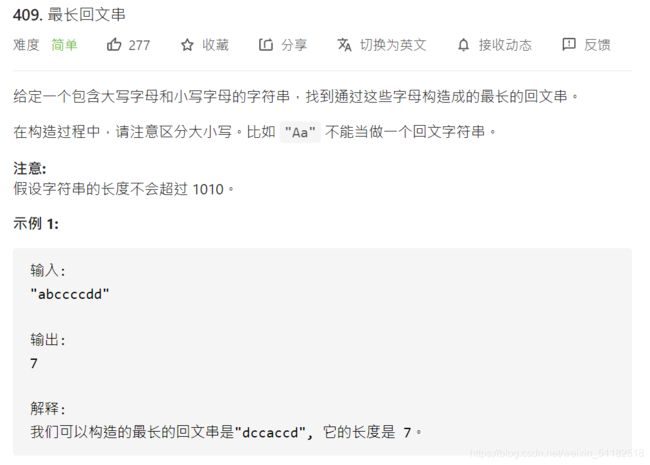
8、Leetcode409:最长回文串
class Solution:
def longestPalindrome(self, s: str) -> int:
n=len(s)
li=[s.count(i)%2 for i in set(s)]
return n - max(0,sum(li)-1)
9、Leetcode 331:验证二叉树的前序序列化
题目描述

解题思路:
如果对于一个节点,它的两个子节点都是"#",那么可以将这一组节点变为#。
例如
9,#,# ——>#,再去和他的上一层进行比较。遍历一遍前序遍历的列表,如果到最后只剩下["#"]表示序列化正常。
代码实现:
class Solution:
def isValidSerialization(self, preorder: str) -> bool:
stack=[]
for i in preorder.split(","):
stack.append(i)
while len(stack)>=3 and stack[-1]==stack[-2]=="#" and stack[-3]!="#":
stack.pop(),stack.pop(),stack.pop()
stack.append("#")
return len(stack)==1 and stack.pop()=="#"
10、Leetcode 705:设计哈希集合
题目描述
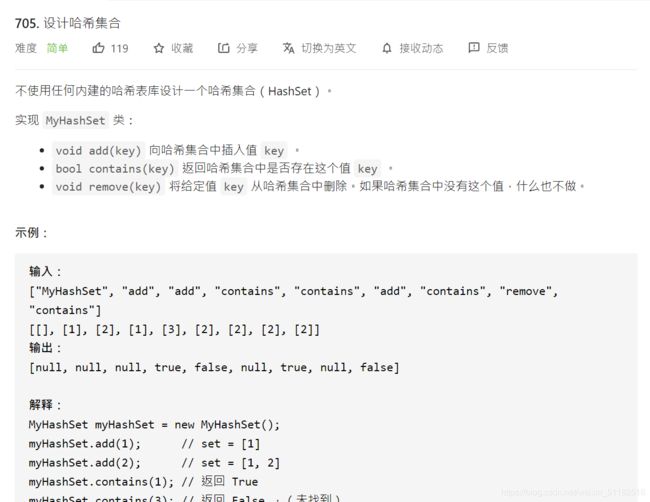
解题思路
对于输入的key使用key%1009作为哈希函数存储,无论是add,remove还是contain都通过查看self.table[hashkey]中是否有当前key来决定操作。self.table是一个列表存储了哈希的键位和值。
代码
class MyHashSet:
def __init__(self):
"""
Initialize your data structure here.
"""
self.buckets=1009
self.table=[[] for i in range(self.buckets)]
def hash(self,key):
#将输入的key进入哈希映射
return key%self.buckets
def add(self, key: int) -> None:
hashkey=self.hash(key)
if key in self.table[hashkey]:
return
self.table[hashkey].append(key)
def remove(self, key: int) -> None:
hashkey=self.hash(key)
if key not in self.table[hashkey]:
return
self.table[hashkey].remove(key)
def contains(self, key: int) -> bool:
"""
Returns true if this set contains the specified element
"""
hashkey=self.hash(key)
if key in self.table[hashkey]:
return True
else:
return False
11、Leetcode 13:罗马数字转整数:
解题思路
- 定义一个字典存储每个罗马数字对应的int值
- 遍历str,如果当前的这个罗马数字对应的int值是小于下一个的,那么就要在输出值减去当前值
- 否则,就加上当前罗马数字对应的十进制数字。
代码
class Solution:
def romanToInt(self, s: str) -> int:
dic={"I":1,"V":5,"X":10,"L":50,"C":100,"D":500,"M":1000}
ans=0
for i in range(len(s)):
if i<len(s)-1 and dic[s[i]]<dic[s[i+1]]:
ans-=dic[s[i]]
else:
ans+=dic[s[i]]
return ans
12、Leetcode 88:合并两个有序数组
解题思路
定义两个指针,分别遍历两个nums。终止点是指针到达m和n为止。
这里边要注意的是要对nums1进行浅拷贝。
因为有可能p和q一个遍历完了,一个还没有遍历完,所以while循环后要把剩下的使用extend补齐。
代码
class Solution:
def merge(self, nums1: List[int], m: int, nums2: List[int], n: int) -> None:
"""
Do not return anything, modify nums1 in-place instead.
"""
nums1_copy=nums1[:m]
nums1[:]=[]
p=0
q=0
while p < m and q<n:
if nums1_copy[p]<=nums2[q]:
nums1.append(nums1_copy[p])
p+=1
else:
nums1.append(nums2[q])
q+=1
nums1.extend(nums1_copy[p:])
nums1.extend(nums2[q:])
13、Leetcode 706:设计哈希映射
此题比较简单,就直接放代码了
class MyHashMap:
def __init__(self):
"""
Initialize your data structure here.
"""
self.map=[-1]*1000001
def put(self, key: int, value: int) -> None:
"""
value will always be non-negative.
"""
self.map[key]=value
def get(self, key: int) -> int:
"""
Returns the value to which the specified key is mapped, or -1 if this map contains no mapping for the key
"""
return self.map[key]
def remove(self, key: int) -> None:
"""
Removes the mapping of the specified value key if this map contains a mapping for the key
"""
self.map[key]=-1
14、Leetcode 54 螺旋矩阵:
解题思路
对于顺时针遍历螺旋矩阵,最难的点在于何时更改方向,从例子中可以看到,更改方向的点都是走到了行和列的边缘,或者遇到已经走过的点。那么对于本题,需要创建的除了一个存储所有螺旋便利的列表,还需要一个列表存储下一个点的行列信息是否已经走过的状态列表。遍历行和列所有的点,只要加入一次方向后,再该方向上不是边界外的点且没有遍历过,该点就可以加入res列表。除此之外,direction的列表的方向应该按顺时针书写。
代码
class Solution:
def spiralOrder(self, matrix: List[List[int]]) -> List[int]:
#统计行和列的数量
row=len(matrix)
col=len(matrix[0])
#所有的元素个数
total=row*col
#建立一个存储是否访问过的矩阵
visited=[[False ] * col for i in range(row)]
#建立一个存储路径的列表
order=[0]*total
#建立顺时针的方向矩阵
direction=[[0,1],[1,0],[0,-1],[-1,0]]
#初始化位置和方向索引
r,c=0,0
direction_idx=0
#开始遍历
for k in range(total):
#向order中添加元素信息
order[k]=matrix[r][c]
#在vistied 中存储路径
visited[r][c]=True
#计算下一个位置的坐标点
next_r=r+direction[direction_idx][0]
next_c=c+direction[direction_idx][1]
#判断这个点是否满足条件
if not (0<=next_r<row and 0<=next_c<col and not visited[next_r][next_c]):
#顺时针更新方向,只需要更新一次方向就可以保证一定可以继续走
direction_idx=(direction_idx+1)%4
#更新r和c的坐标
r+=direction[direction_idx][0]
c+=direction[direction_idx][1]
return order
15、 Leetcode 14 最长公共前缀
题目描述

解题思路
Approach 1:纵向查找
纵向查找,只需要以第一个单词的长度为基准,对比其他单词在每一位上是否相同,如果出现了不同或已经到达了任何一个词的长度,只需要返回前面的i-1个单词即可。
Approach 2: 分治
加入这个strs有四个单词,那么把它分成两份,再对其中每一份进行两两之间的比较,返回两两之间的最长公共前缀,再进行回溯,因为最长公共前缀是所有单词的公共前缀。终止条件是左边界等于右边界。
代码
#纵向搜索
class Solution:
def longestCommonPrefix(self, strs: List[str]) -> str:
if not strs:
return ""
length=len(strs[0])
count=len(strs)
for i in range(length):
if any(i==len(strs[j]) or strs[j][i]!=strs[0][i] for j in range(1,count)):
return strs[0][:i]
#如果都相同
return strs[0][:length]
class Solution:
def longestCommonPrefix(self, strs: List[str]) -> str:
#分治的思想
def dfs(start,end):
#终止条件:
if start == end:
return strs[start]
#将strs里面的字母分开
mid=(start+end)//2
#递归左右两边
left=dfs(start,mid)
right=dfs(mid+1,end)
#对比两个返回的长度,取小的那个
min_length=min(len(left),len(right))
#遍历较短的单词
for j in range(min_length):
#一旦他们出现了不相等的位置
if left[j]!=right[j]:
return left[:j]
#如果都相同,return较短的
return left[:min_length]
return "" if not strs else dfs(0,len(strs)-1)
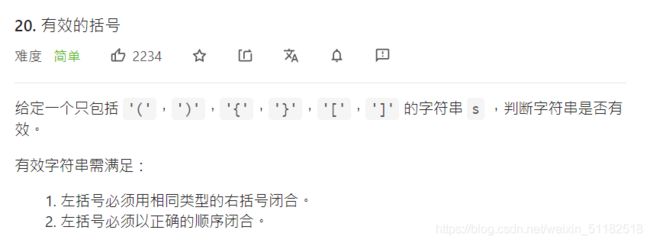
16、Leetcode 20:有效的括号
解题思路
采用栈的思想,遍历字符串中的每一个括号,分成四类讨论:
- 如果是")“且上一个也是”(",那么把上一个出栈
- 如果是”]“且栈的上一个是"[",那么把上一个出栈
- 如果是"}“且栈的最后一个是”{",那么把栈的最后一个出栈。
- 如果不满足上述四个,将当前括号类型压栈。
如果最后stack的长度为0说明符合标准,返回True,否则返回False。
代码
class Solution:
def isValid(self, s: str) -> bool:
stack=[]
n=len(s)
for i in s:
if stack and i=="]" and stack[-1]=="[":
stack.pop()
elif stack and i==")" and stack[-1]=="(":
stack.pop()
elif stack and i=="}" and stack[-1]=="{":
stack.pop()
else:
stack.append(i)
return True if len(stack)==0 else False
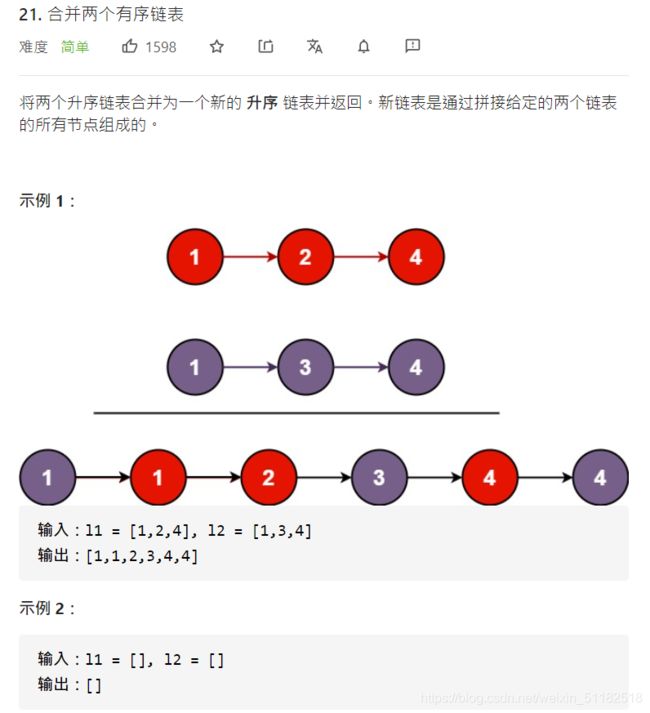
17、Leetcode 21:合并两个有序的链表
题目描述
递归方法
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution:
def mergeTwoLists(self, l1: ListNode, l2: ListNode) -> ListNode:
if l1 is None:
return l2
elif l2 is None:
return l1
elif l1.val > l2.val:
l2.next=self.mergeTwoLists(l1,l2.next)
return l2
else:
l1.next=self.mergeTwoLists(l1.next,l2)
return l1
迭代方法
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution:
def mergeTwoLists(self, l1: ListNode, l2: ListNode) -> ListNode:
#迭代的方法
#建立一个节点
head=ListNode(-1)
#定义指针
pre=head
while l1 and l2:
if l1.val>l2.val:
pre.next=l2
l2=l2.next
else:
pre.next=l1
l1=l1.next
#比较完要移动一次指针
pre=pre.next
#将剩下的没有添加完的添加进head
pre.next=l1 if l1 is not None else l2
return head.next
18、Leetcode 139:单词拆分问题
解题思路
本题使用动态规划解决,建立一个dp列表长度为n+1,每个位置储存的状态为false,dp[i]表示从str[:i]能否满足题意,遍历str的长度,遍历每个i前面的所有字母,只要s[j-1:i]存在在字典,那么dp[i]和dp[j-1]的状态是一样的。
代码
class Solution:
def wordBreak(self, s: str, wordDict: List[str]) -> bool:
#建立一个DP列表
n=len(s)
dp=[False]*(n+1)
#初始化
dp[0]=True
#遍历
for i in range(1,n+1):
for j in range(i,-1,-1):
if s[j-1:i] in wordDict:
dp[i]|=dp[j-1]
return dp[n]
19、剑指Offer 29:顺时针打印矩阵
该题和螺旋矩阵相同,直接上代码
class Solution:
def spiralOrder(self, matrix: List[List[int]]) -> List[int]:
#计算行的长度
row=len(matrix)
if row==0:
return []
#计算列的长度
col=len(matrix[0])
#计算有多少个数字
total=col*row
#定义一个存储访问的矩阵
visted=[[False]*col for i in range(row)]
#定义一个最后输出的矩阵
res=[0]*total
#定义方向的列表
direction=[(0,1),(1,0),(0,-1),(-1,0)]
#定义col和row的起始位置
r,c=0,0
direction_id=0
#开始遍历
for i in range(total):
res[i]=matrix[r][c]
visted[r][c]=True
#定义direction id
new_r=r+direction[direction_id][0]
new_c=c+direction[direction_id][1]
#判断这个点是否满足条件
if not (0<=new_r<row and 0<=new_c<col and not visted[new_r][new_c]):
direction_id=(direction_id+1)%4
r+=direction[direction_id][0]
c+=direction[direction_id][1]
return res
20、LCP 11: 期望个数统计
class Solution:
def expectNumber(self, scores: List[int]) -> int:
return len(set(scores))
21、Leetcode 59:螺旋矩阵II
题目描述

解题思路
这道题和原本的螺旋矩阵类似,但是不需要维护一个状态的矩阵,只需要判断matrix中下一个位置的值是否为初始值0。
代码
class Solution:
def generateMatrix(self, n: int) -> List[List[int]]:
#设定行和列的数量
row,col=n,n
#建立一个填入的矩阵
matrix=[[0]*n for _ in range(n)]
#建立方向
direction=[(0,1),(1,0),(0,-1),(-1,0)]
#建立初始坐标和方向索引
r,c,d=0,0,0
#开始添加
for i in range(n*n):
matrix[r][c]=i+1
new_r=r+direction[d][0]
new_c=c+direction[d][1]
#查看下一个坐标位置是否符合规则
if not(0<=new_c<col and 0<=new_r<row and matrix[new_r][new_c]==0):
#方向顺时针转动一次
d=(d+1)%4
#更新坐标
r+=direction[d][0]
c+=direction[d][1]
return matrix
22、Leetcode 101 : 对称二叉树
代码实现
Approach 1:递归
使用递归做,就是定义函数不断地去判断每个左节点下的左子节点,和右节点下的右子节点和左节点下的右子节点和右节点下的左子节点是否相同。这里比较麻烦的是终止条件:
- 条件1:如果left和right都为空,为true:not(left or right)
- 条件2:如果left和right 有一个为空,为False:not(left and right)
- 条件3:如果left和right的val不同,为False
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def isSymmetric(self, root: TreeNode) -> bool:
if not root:
return True
def dfs(left,right):
#left代表左叶节点,left代表右叶节点
#终止条件1:如果left和right为空
if not (left or right):
return True
#终止条件2:如果left和right有一个为空:
if not (left and right):
return False
#终止条件3,left和right不相等
if left.val!=right.val:
return False
#进入递归
return dfs(left.left,right.right) and dfs(left.right,right.left)
return dfs(root.left,root.right)
Approach 2:队列迭代
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def isSymmetric(self, root: TreeNode) -> bool:
#建立一个队列
queue=collections.deque()
queue.extend([root.left,root.right])
while queue:
#拿出第一对
left=queue.popleft()
right=queue.popleft()
#如果left和right都为空
if not (left or right):
continue
#如果一个为空:
if not (left and right):
return False
if left.val!=right.val:
return False
#将left的左节点,right的右节点添加队列
queue.extend([left.left,right.right])
#将left的右节点,right的左节点添加队列
queue.extend([left.right,right.left])
return True
23、Leetcode 115:不同的子序列
解题思路
转移方程的话已经在代码中写到了,解题思路感觉这个大佬写的最清晰,即如果当前对比的位置字符相同,我可以选择进行匹配或者不进行匹配,因为从右往左的顺序进行匹配的话,即使相同前面可能也会有相同的,所以有两种选择。

代码实现
class Solution:
def numDistinct(self, s: str, t: str) -> int:
#统计两个字符串的长度
m,n=len(s),len(t)
#以t为子串,如果t比s长,不符合题意
if m<n:
return 0
#建立储存的状态矩阵
dp=[[0]*(n+1) for _ in range(m+1)]
#初始化,如果n=0,那么它可以使s的任何子串
for i in range(m+1):
dp[i][n]=1
#如果m=0,没有字串
#开始遍历
for i in range(m-1,-1,-1):
for j in range(n-1,-1,-1):
#如果当前字母匹配
if s[i]==t[j]:
#那么有可能是从s+1,j+1转移,也可能是s+1,j转移
dp[i][j]=dp[i+1][j+1]+dp[i+1][j]
else:
#如果不相等,只能考虑s+1,j
dp[i][j]=dp[i+1][j]
return dp[0][0]
24、Leetcode 1603 :设计停车系统
解题思路
这题想通过还是很简单的,不做赘述了。
代码实现
class ParkingSystem:
def __init__(self, big: int, medium: int, small: int):
self.big=big
self.medium=medium
self.small=small
def addCar(self, carType: int) -> bool:
if carType==3:
if self.small>=1:
self.small-=1
return True
else:
return False
elif carType==2:
if self.medium>=1:
self.medium-=1
return True
else:
return False
else:
if self.big>=1:
self.big-=1
return True
else:
return False
25、Leetcode 290:单词规律
解题思路
- 使用两个哈希表
word2char:存储当前词key对应的字母value
char2word:存储当前字母key对应的单词value - 那么判断其为false的就有两个条件
1、当前词已经出现在word2char中了,但对应的char并不是当前的char
2、当前char已经出现在char2word里了,但对应的word不是当前的word - 使用zip(pattern,word_list)进行打包遍历
代码实现
class Solution:
def wordPattern(self, pattern: str, s: str) -> bool:
word2chr={}
chr2word={}
#如果长度不相等,直接返回错
word_list=s.split()
if len(pattern)!=len(word_list):
return False
for char,word in zip(pattern,word_list):
#如果词在词典中出现,但对应的字母和word2chr的不同
#如果字母在字典中出现,但对应的词和chr2word存储的不同
if (word in word2chr and word2chr[word] !=char) or (char in chr2word and chr2word[char]!=word):
return False
word2chr[word]=char
chr2word[char]=word
return True
26、Leetcode 6:Z字形变换
解题思路
把这道题想得简单些,加入输入的numsRows有三行,那么添加字符串中的顺序应该是012|1|012|1
也就是说只要定义一个变量去存储方向状态即可
- i==0时,flag为+1
- 达到i==row-1后,flag为-1
代码实现
class Solution:
def convert(self, s: str, numRows: int) -> str:
if numRows < 2: return s
res = ["" for _ in range(numRows)]
i, flag = 0, -1
for c in s:
res[i] += c
if i == 0 or i == numRows - 1: flag = -flag
i += flag
return "".join(res)
作者:jyd
链接:https://leetcode-cn.com/problems/zigzag-conversion/solution/zzi-xing-bian-huan-by-jyd/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
27、Leetcode 914:卡牌分组
代码实现+步骤详解
class Solution:
def hasGroupsSizeX(self, deck: List[int]) -> bool:
#统计牌组中每一种牌出现的次数
count_list=collections.Counter(deck)
#统计长度
n=len(deck)
#对X进行遍历
for x in range(2,n+1):
#条件1:x是长度的约数
if n%x==0:
#条件2:x是每个牌出现次数的约数
if all(v%x==0 for v in count_list.values()):
return True
#如果遍历完所有x取值的可能都没达到条件,返回False
return False
28、面试题 01.08 零矩阵:
代码实现
第一次遍历,存储matrix位置为0的row和col,第二次遍历将row和
col为0的所有位置都变成0。
class Solution:
def setZeroes(self, matrix: List[List[int]]) -> None:
"""
Do not return anything, modify matrix in-place instead.
"""
row=len(matrix)
col=len(matrix[0])
r,c=[0]*row,[0]*col
for i in range(row):
for j in range(col):
if matrix[i][j]==0:
r[i]=1
c[j]=1
for i in range(row):
for j in range(col):
if r[i]==1 or c[j]==1:
matrix[i][j]=0
29、Leetcode 150:逆波兰表达式求值
解题思路
维护一个栈,遍历tokens
- 如果token为数字,压栈
- 当遇到了加减乘除符号,拿出栈的后两个进行计算后,将计算值压栈。
- 返回stack中最后的值。
代码实现
class Solution:
def evalRPN(self, tokens: List[str]) -> int:
stack=[]
for token in tokens:
if token in ["+","-","/","*"]:
b=stack.pop()
c=stack.pop()
if token=="*":
stack.append(b*c)
elif token=="/":
stack.append(int(c/b))
elif token=="+":
stack.append(b+c)
else:
stack.append(c-b)
else:
stack.append(int(token))
return int(stack[-1])
30、Leetcode 232:用栈实现队列
题目描述
解题思路
这种简单的题是真实存在的么…
代码实现
class MyQueue:
def __init__(self):
"""
Initialize your data structure here.
"""
self.queue=[]
def push(self, x: int) -> None:
"""
Push element x to the back of queue.
"""
self.queue.append(x)
def pop(self) -> int:
"""
Removes the element from in front of queue and returns that element.
"""
return self.queue.pop(0)
def peek(self) -> int:
"""
Get the front element.
"""
return self.queue[0]
def empty(self) -> bool:
"""
Returns whether the queue is empty.
"""
return len(self.queue)==0
31、Leetcode 503:下一个更大元素II
题目描述
解题思路
做多了dp感觉这种题还是很简单的。主要说一下三个核心点:
- 1、因为是循环数组,所以遍历n*2-1次,每个位置用i对n取模达到定位
- 2、代码中,res列表存储的是每个位置的下一个最大值,stack中存储的是nums中每个的下标。
- 3、对于当前nums[i]的值来说,遍历stack中其他的下标,如果stack中其他下标对应的值小于了nums[i],那么先要将res对应的位置添加nums[i],说明这些位置的下一个最大值就是nums[i],然后再把nums[i]压栈去寻找nums[i]的下一个最大元素。
代码实现
class Solution:
def nextGreaterElements(self, nums: List[int]) -> List[int]:
n=len(nums)
#维护一个列表储存每个下标对应的下一个最大值
res=[-1]*n
#建立一个栈,存储的是下标
stack=[]
#因为是循环数组,遍历2n次
for i in range(n*2-1):
#只要栈中的元素比当前元素小,就pop
while stack and nums[stack[-1]]<nums[i%n]:
res[stack.pop()]=nums[i%n]
stack.append(i%n)
return res
32、Leetcode 131:分割回文串
题目描述
![]()
解题思路
这道题分为递归和dp两个部分
1、dp部分::判断
判断i到j是否为回文串,如果当前i和j的位置相等,且i+1到j-1的位置也是回文串,那么 d p [ i ] [ j ] dp[i][j] dp[i][j]是回文串。
2、递归部分::遍历
对于当前位置的i,遍历i后面的所有元素,判断i,j是否为回文串,如果是,将level中存储这部分的值,因为i,j已经是回文串了,那么要对j+1开始判断是j+1,n是否为回文串,当j到达n时,把这部分的值存储到res中。返回上一层,每返回一层还要讲该层的信息删除pop掉。
代码实现
class Solution:
def partition(self, s: str) -> List[List[str]]:
n=len(s)
#DP部分,表示i-j部分的字符串是否为回文串的判断
dp=[[True]*n for _ in range(n)]
for i in range(n-1,-1,-1):
for j in range(i+1,n):
#i=j是回文串的条件是当前元素对应值相等且i+1:j-1也是回文串
dp[i][j]=dp[i+1][j-1] and s[i]==s[j]
#存储所有结果
res=[]
#递归过程中存储每个结果
level=[]
def dfs(i):
#终止条件:
if i==n:
res.append(level[:])
return
#对于每个i进行分析
for j in range(i,n):
#如果当前是回文串
if dp[i][j]:
level.append(s[i:j+1])
#对于j+1开始判断
dfs(j+1)
#删除前面的可能
level.pop()
dfs(0)
return res
33、Leetcode 92:反转链表II
题目描述
解题思路
- 先将指针定位到反转区域的前一个元素,定义pre,cur,next
- 对于需要反转的区域,每次不算的把pre cur next的位置翻转为pre next cur。pre是固定的
代码实现
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution:
def reverseBetween(self, head: ListNode, left: int, right: int) -> ListNode:
#设置头节点
dummy=ListNode(-1)
dummy.next=head
#前节点
pre=dummy
#定位到left的前一个位置
for i in range(left-1):
pre=pre.next
#定位到left的第一个位置
cur=pre.next
#遍历需要反转的区域
for j in range(right-left):
#找到前一个节点
next=cur.next
#将cur指向前一个的前一个
cur.next=next.next
#将next指向cur
next.next=pre.next
#将pre指向next
pre.next=next
return dummy.next
第二章 二叉树/N叉树
1、Leetcode 94:二叉树的中序遍历
使用递归的思想
使用递归的思想即为对于每个根节点都按照左根右的方式进行遍历,递归的思路即为先对根节点的左子节点进行递归,然后打印或添加,然后再对根节点的右子节点进行递归。如果对于当前递归层的节点来说,它不是root,则返回上一层递归操作。
代码实现:
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def inorderTraversal(self, root: TreeNode) -> List[int]:
res=[]
def dfs(root):
if not root:
return
dfs(root.left)
res.append(root.val)
dfs(root.right)
dfs(root)
return res
颜色标记法
使用stack的思想,先进后出。定义新的节点为白色,已经遍历过的节点为灰色,如果第一次看到的节点是白色,就要把当前节点的按照右,中,左的顺序依次入栈。同时还要不算的出栈,出栈的顺序即为左、中、右。对于每一次节点的进栈,它本身的节点已经被看过了,将其变成灰色标记存入栈中,即下次出栈出到这个节点时,它本身就是灰色,不需要处理,直接出栈即可。而它的左子节点和右子节点还没有被看过,需要先进栈再出栈才算被看过,所以标记为白色。
代码实现:
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def inorderTraversal(self, root: TreeNode) -> List[int]:
res=[]
white,gray=0,1
stack=[(white,root)]
while stack:
color,node=stack.pop()
if node is None:
continue
if color==white:
stack.append((white,node.right))
stack.append((gray,node))
stack.append((white,node.left))
else:
res.append(node.val)
return res
维护一个栈迭代的思想
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def inorderTraversal(self, root: TreeNode) -> List[int]:
if not root:
return []
res=[]
stack=[root]
while stack:
while root.left:
stack.append(root.left)
root=root.left
cur=stack.pop()
res.append(cur.val)
if cur.right:
stack.append(cur.right)
root=cur.right
return res
2、Leetcode 144:二叉树的前序遍历
递归的思路
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def preorderTraversal(self, root: TreeNode) -> List[int]:
res=[]
def dfs(root):
if root:
res.append(root.val)
dfs(root.left)
dfs(root.right)
dfs(root)
return res
颜色标记法
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def preorderTraversal(self, root: TreeNode) -> List[int]:
res=[]
white,gray=0,1
stack=[(white,root)]
while stack:
color,node=stack.pop()
if node is None:
continue
if color==white:
stack.append((white,node.right))
stack.append((white,node.left))
stack.append((gray,node))
else:
res.append(node.val)
return res
迭代的方法维护一个栈
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def preorderTraversal(self, root: TreeNode) -> List[int]:
if not root:
return []
res=[]
stack=[]
node=root
while stack or node:
while node:
res.append(node.val)
stack.append(node)
node=node.left
node=stack.pop()
node=node.right
return res
3、Leetcode 145:二叉树的后序遍历
使用递归的思想
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def postorderTraversal(self, root: TreeNode) -> List[int]:
if not root:
return []
res=[]
def dfs(root):
if root:
dfs(root.left)
dfs(root.right)
res.append(root.val)
dfs(root)
return res
使用颜色标记法
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def postorderTraversal(self, root: TreeNode) -> List[int]:
if not root:
return []
white, gray=0,1
stack=[(white,root)]
res=[]
while stack:
color , node =stack.pop()
if not node:
continue
if color==white:
stack.append((gray,node))
stack.append((white,node.right))
stack.append((white,node.left))
else:
res.append(node.val)
return res
使用迭代的思想
实现左右根的思路感觉很难,所以将前序遍历中的根左右,变为根右左再逆序就得到了左右根。
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def postorderTraversal(self, root: TreeNode) -> List[int]:
res,stack=[],[]
node=root
while node or stack:
while node:
res.append(node.val)
stack.append(node)
node=node.right
cur=stack.pop()
node=cur.left
return res[::-1]
4、N叉树的后续遍历
使用递归的思想
对于N叉树的后续遍历其实与二叉树差不多,只不过对于每个节点,需要完成一次遍历,按照左右根的顺序进行遍历。
"""
# Definition for a Node.
class Node:
def __init__(self, val=None, children=None):
self.val = val
self.children = children
"""
class Solution:
def postorder(self, root: 'Node') -> List[int]:
res=[]
def dfs(root):
if root:
for node in root.children:
dfs(node)
res.append(root.val)
dfs(root)
return res
颜色标记法
依然可以使用颜色标记法,遍历的顺序为12345根,所以压栈顺序应该为根54321,故遍历每个node的子节点时,应该逆序遍历。
"""
# Definition for a Node.
class Node:
def __init__(self, val=None, children=None):
self.val = val
self.children = children
"""
class Solution:
def postorder(self, root: 'Node') -> List[int]:
white,gray=0,1
res=[]
stack=[(white,root)]
while stack:
color,node=stack.pop()
if not node:
continue
if color==white:
stack.append((gray,node))
for node_child in node.children[::-1]:
stack.append((white,node_child))
else:
res.append(node.val)
return res
迭代法
"""
# Definition for a Node.
class Node:
def __init__(self, val=None, children=None):
self.val = val
self.children = children
"""
class Solution:
def postorder(self, root: 'Node') -> List[int]:
if not root:
return []
res=[]
stack=[root]
while stack:
node=stack.pop()
stack.extend(node.children)
res.append(node.val)
return res[::-1]
5、Leetcode 589:N叉树的前序遍历:
递归的方法:
"""
# Definition for a Node.
class Node:
def __init__(self, val=None, children=None):
self.val = val
self.children = children
"""
class Solution:
def preorder(self, root: 'Node') -> List[int]:
res=[]
def dfs(root):
if root:
res.append(root.val)
for child in root.children:
dfs(child)
dfs(root)
return res
颜色标记法
"""
# Definition for a Node.
class Node:
def __init__(self, val=None, children=None):
self.val = val
self.children = children
"""
class Solution:
def preorder(self, root: 'Node') -> List[int]:
white,gray=0,1
stack=[(white,root)]
res=[]
while stack:
color,node=stack.pop()
if not node:
continue
if color==white:
for child in node.children[::-1]:
stack.append((white,child))
stack.append((gray,node))
else:
res.append(node.val)
return res
迭代法
"""
# Definition for a Node.
class Node:
def __init__(self, val=None, children=None):
self.val = val
self.children = children
"""
class Solution:
def preorder(self, root: 'Node') -> List[int]:
if not root:
return []
stack=[root]
res=[]
while stack:
node=stack.pop()
stack.extend(node.children[::-1])
res.append(node.val)
return res
6、Leetcode 429:N叉树的层序遍历
迭代法:
解题思路
因为返回的格式是每一层的元素都由一个列表格式返回,且层序遍历是对于每一层都从左到右进行遍历,所以使用队列会比使用栈好,队列左出右进,边可满足层序遍历的条件。具体代码思路如下。
- res列表用来存储结果。
- 调用collections.deque建立一个队列,将[root]添加进队列。
- 只要队列不为空就进行循环。
- 建立一个queue列表存储每一层的元素
- 每次在内层循环一个队列的长度,每次都从stack中取出一个层,然后把它添加到queue里,再把这个元素的所有孩子节点都extend到队列中。
"""
# Definition for a Node.
class Node:
def __init__(self, val=None, children=None):
self.val = val
self.children = children
"""
class Solution:
def levelOrder(self, root: 'Node') -> List[List[int]]:
if not root:
return []
res=[]
stack=collections.deque([root])
while stack:
queue=[]
for _ in range(len(stack)):
node=stack.popleft()
queue.append(node.val)
stack.extend(node.children)
res.append(queue)
return res
第三章:哈希表
哈希表存储的方式:哈希函数映射到一个int的index的位置。
One of approach of hash function:对于一个字符串转为ascii值相加
好的哈希函数可以让数值在哈希表中尽量分散,避免哈希碰撞。
如果发生哈希碰撞,可以对一个位置加入一个链表存储这几个碰撞的值,但如果碰撞的太多,遍历会变得麻烦。
查询添加,删除的复杂度都为O(1)。
1、Leetcode 242:有效的字母异位
核心思路
将每个字符串中分别出现的词作为key,词频作为value,存储在两个字典中。最后判断两个字典知否相等即可。
from collections import defaultdict
class Solution:
def isAnagram(self, s: str, t: str) -> bool:
dict1=defaultdict(int)
dict2=defaultdict(int)
for i in s:
dict1[i]+=1
for j in t:
dict2[j]+=1
return True if dict1==dict2 else False
2、 Leetcode 49:字母异位词分组
问题描述:

核心思想
建立一个哈希表,遍历列表中的每个单词,对单词进行sorted后的字符串作为key,value的数据类型为list,每次遇到字母异位词就直接append到对应的key中。
class Solution:
def groupAnagrams(self, strs: List[str]) -> List[List[str]]:
dict1=collections.defaultdict(list)
for token in strs:
key="".join(sorted(token))
dict1[key].append(token)
res=[]
for key,value in dict1.items():
res.append(value)
return res
方法2:计数
建立一个长度为26的count列表,每个位置表示对于一个单词每个字母出现的次数,字母异位词的两个词会有相同的count列表。将count作为key,字母异位词的list作为value。
class Solution:
def groupAnagrams(self, strs: List[str]) -> List[List[str]]:
mp = collections.defaultdict(list)
for st in strs:
counts = [0] * 26
for ch in st:
counts[ord(ch) - ord("a")] += 1
# 需要将 list 转换成 tuple 才能进行哈希
mp[tuple(counts)].append(st)
return list(mp.values())
3、Leetcode1:两数之和
题目描述
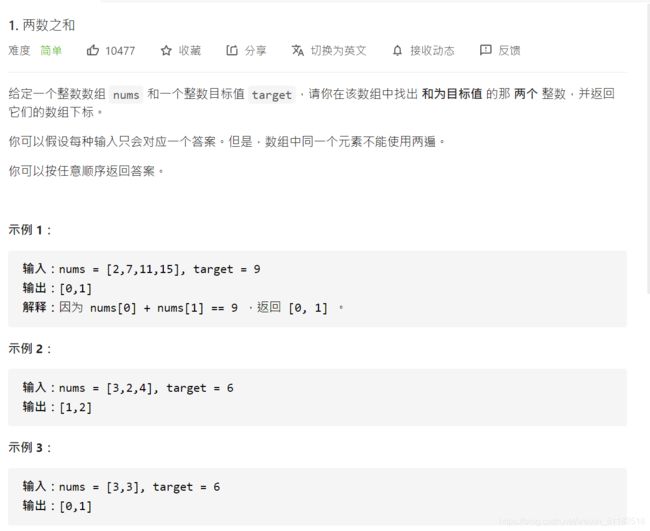
思路
首先遍历一次列表,将列表的值和索引作为key和value存入字典。再遍历一次列表,如果对于当前位置的值被target减去存在于dict的key中且它们的索引位置不同,那么它们满足条件,直接返回即可。
class Solution:
def twoSum(self, nums: List[int], target: int) -> List[int]:
dict1=collections.defaultdict(int)
for i in range(len(nums)):
dict1[nums[i]]=i
res=[]
for j in range(len(nums)):
if target-nums[j] in dict1 and j!=dict1[target-nums[j]]:
return [dict1[target-nums[j]],j]
第四章 递归
- 1、添加终止条件
- 2、处理当前层逻辑
- 3、进入下一层的递归
思维要点:
1、不要人肉递归
2、找到最近最简方法,将其拆解成可重复解决的问题(重复子问题)
3、数学归纳法思维。
1、 Leetcode-70: 爬楼梯问题
class Solution:
def climbStairs(self, n: int) -> int:
if n<=2:
return n
#对于n阶台阶就是n-2和n-1选一种
f1,f2,f3=1,2,3
for i in range(3,n+1):
f3=f1+f2
f1=f2
f2=f3
return f3
2、Leetcode-22:括号生成问题
解题思路
定义左括号left和右括号right,它们的终止条件都为到达n停止。但是对于左括号的要求仅仅为小于等于n,但对于右括号,只有已经加入左括号后,右括号才可以加入。即对于每一层的计算,考虑是在基础上加left还是right。
代码
class Solution:
def generateParenthesis(self, n: int) -> List[str]:
ans=[]
def generate(left,right,s):
if left==n and right==n:
ans.append("".join(s))
return
if left<n:
s.append("(")
generate(left+1,right,s)
s.pop()
if right<left:
s.append(")")
generate(left,right+1,s)
s.pop()
left,right=0,0
s=[]
generate(left,right,s)
return ans
3、Leetcode 98:验证二叉搜索树
解题思路:
对于当前传入节点,要小于它的下届大于它的上届的话即不满足条件,再对它的左子节点右子节点进行递归,分别判断,此时左子节点的递归的上界变成该node的val,右子节点的递归的下界变成该node的val。
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def isValidBST(self, root: TreeNode) -> bool:
def search(node,lower=float("-inf"),upper=float("inf")):
if not node:
return True
value=node.val
if value <= lower or value>=upper:
return False
if not search(node.right,value,upper):
return False
if not search(node.left,lower,value):
return False
return True
return search(root)
4、Leetcode226:翻转二叉树
解题思路
对于每个节点,都需要把当前节点的左子节点和右子节点进行翻转。层层递归,当没有左子节点和右子节点后,逐层返回,把root.left和root.right交换位置即可。
代码
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def invertTree(self, root: TreeNode) -> TreeNode:
if not root:
return root
left=self.invertTree(root.left)
right=self.invertTree(root.right)
root.left,root.right=right,left
return root
5、Leetcode104:二叉树的最大深度
解题思路
如果root存在就分别递归它的左子树和右子树,左子树和右子树的深度的最大值加1(root层)即为当前树的最大深度。
代码
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def maxDepth(self, root: TreeNode) -> int:
if root is None:
return 0
else:
left=self.maxDepth(root.left)
right=self.maxDepth(root.right)
return max(left,right)+1
6、Leetcode111:二叉树的最小深度
解题思路
首先可以想到使用深度优先搜索的方法,遍历整棵树,记录最小深度。对于每一个非叶子节点,我们只需要分别计算其左右子树的最小叶子节点深度。这样就将一个大问题转化为了小问题,可以递归地解决该问题。
代码实现
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def minDepth(self, root: TreeNode) -> int:
if root is None:
return 0
if not root.left and not root.right:
return 1
min_depth=10**10
if root.left:
min_depth=min(self.minDepth(root.left),min_depth)
if root.right:
min_depth=min(self.minDepth(root.right),min_depth)
return min_depth+1
7、Leetcode509:斐波那契数列
Approach 1:动态规划
class Solution:
def fib(self, n: int) -> int:
if n<=1:
return n
f1,f2,f3=0,1,1
for i in range(2,n+1):
f3=f1+f2
f1,f2=f2,f3
return f3
class Solution:
def fib(self, n: int) -> int:
sqr=5**0.5
fn=(((1+sqr)/2)**n-((1-sqr)/2)**n)/sqr
return int(fn)
Approach 3:使用列表存储动态规划
class Solution:
def fib(self, n: int) -> int:
dp=[1 for i in range(n+1)]
dp[0]=0
for j in range(2,n+1):
dp[j]=dp[j-1]+dp[j-2]
return dp[n]
Approach 4: 直接递归
class Solution:
def fib(self, n: int) -> int:
if n <=1:
return n
return self.fib(n-1)+self.fib(n-2)
8、Leetcode 297:二叉树的序列化和反序列化
代码
# Definition for a binary tree node.
# class TreeNode(object):
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Codec:
def serialize(self, root):
"""Encodes a tree to a single string.
:type root: TreeNode
:rtype: str
"""
if not root:
return ""
res=[]
queue=collections.deque([root])
while queue:
node=queue.popleft()
if node:
res.append(str(node.val))
queue.append(node.left)
queue.append(node.right)
else:
res.append("None")
return "[" + ",".join(res)+"]"
def deserialize(self, data):
"""Decodes your encoded data to tree.
:type data: str
:rtype: TreeNode
"""
if not data:
return []
dataList=data[1:-1].split(",")
root=TreeNode(int(dataList[0]))
queue=collections.deque([root])
i=1
while queue:
node=queue.popleft()
if dataList[i]!="None":
node.left=TreeNode(int(dataList[i]))
queue.append(node.left)
i+=1
if dataList[i]!="None":
node.right=TreeNode(int(dataList[i]))
queue.append(node.right)
i+=1
return root
9、Leetcode236:二叉树的公共祖先
题目描述

解题思路
解决这道题的核心思路是找到从根开始到这两个节点的路径,并以列表的形式返回。第二步是选择那个长度较短的路径,遍历这两个路径,当到达一个位置使得两个路径的节点不同是,说明两条路径在这个位置的根节点处分开了,那么返回当前位置上一个位置的元素。如果遍历为较短的路径,都没有出现路径的不同,说明较段路径的节点在较长路径的路径内,直接返回较短路径的节点即可。
代码
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
def back(node,res,path,target):
if not node:
return
if node==target:
path.append(node)
res.extend(path[:])
return
path.append(node)
back(node.left,res,path,target)
back(node.right,res,path,target)
path.pop()
res_q=[]
res_p=[]
back(root,res_p,[],p)
back(root,res_q,[],q)
if len(res_p)>len(res_q):
res_p,res_q=res_q,res_p
for i in range(len(res_p)):
if res_p[i]!=res_q[i]:
return res_p[i-1]
return res_p[-1]
10、Leetcode 105:从前序与中序遍历序列构造二叉树
解题思路
- 1、前序遍历的第一个为整棵树的根节点
- 2、使用这个根节点定位到中序遍历的根节点所在位置,那么该位置左边全为左子树,左边的长度如果记为l,右边全为右子树。
- 3、对于前序遍历,根节点后面一个位置到l的距离也是左子树。
- 4、使用递归
- 5、建立一个哈希表,储存中序遍历中node的值和index对应关系
代码实现
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def buildTree(self, preorder: List[int], inorder: List[int]) -> TreeNode:
def dfs(pre_left:int,pre_right:int,in_left:int,in_right:int):
if pre_left>pre_right:
return None
root1=preorder[pre_left]
#定位到根在中序遍历的位置
root_idx=index[root1]
#构建根节点
root=TreeNode(root1)
#计算根的左子树的个数
nums=root_idx-in_left
#开始进行递归
root.left=dfs(pre_left+1,pre_left+nums,in_left,root_idx-1)
root.right=dfs(pre_left+nums+1,pre_right,root_idx+1,in_right)
return root
n=len(preorder)
index={k:i for i,k in enumerate(inorder)}
return dfs(0,n-1,0,n-1)
11、 Leetcode 77: permutation
题目描述

解题思路
从n个数中取k个进行组合。这道题主要是使用递归的思想,遍历n个数,先选择第一个数,加入一个列表存储,再对后面的数进行递归,直到储存列表达到k个数,把这个列表添加到结果的大列表里。
代码
class Solution:
def combine(self, n: int, k: int) -> List[List[int]]:
res=[]
def backtrace(i,temp):
if len(temp)==k:
res.append(temp)
return
for j in range(i,n+1):
backtrace(j+1,temp+[j])
backtrace(1,[])
return res
12、Leetcode 46:全排列
题目描述

这道题和第一章第七题思路类似,但不需要考虑重复的数字。
代码
class Solution:
def permute(self, nums: List[int]) -> List[List[int]]:
res=[]
def dfs(x):
if x==len(nums)-1:
res.append(nums[:])
return
for i in range(x,len(nums)):
nums[i],nums[x]=nums[x],nums[i]
dfs(x+1)
nums[i],nums[x]=nums[x],nums[i]
dfs(0)
return res
13、Leetcode 47:全排列II
代码实现
class Solution:
def permuteUnique(self, nums: List[int]) -> List[List[int]]:
res=[]
def dfs(x):
if x==len(nums)-1:
res.append(nums[:])
return
dic=set()
for i in range(x,len(nums)):
if nums[i] in dic:
continue
dic.add(nums[i])
nums[i],nums[x]=nums[x],nums[i]
dfs(x+1)
nums[i],nums[x]=nums[x],nums[i]
dfs(0)
return res
第五章 动态规划
分治+最优子结构
将一个复杂的问题分解成很多简单的子问题
关键点
- 动态规划和递归没有根本上的区别
- 共性:找到重复子问题
- 差异性:最优子结构,中途可以淘汰次优解
1、Leetcode 62:不同路径
- 核心:对于没有障碍物的,每一个点要么从上面过来,要么从左面过来。
- 特殊情况:最左边的一列和最上面的一行只能平行的过来,没有第二条路。
代码实现
Approach 1
每一个位置都由左边或者上边状态转移得到
class Solution:
def uniquePaths(self, m: int, n: int) -> int:
#建立dp矩阵
dp=[[0] *(n+1) for i in range(m+1)]
for i in range(m+1):
dp[i][1]=1
for j in range(n+1):
dp[1][j]=1
#开始循环
for i in range(2,m+1):
for j in range(2,n+1):
dp[i][j]=dp[i-1][j]+dp[i][j-1]
return dp[m][n]
Approach 2
只需要维护一层的状态列表就可以,因为每个点的状态等于上面的状态加左边的状态,在累加每一行的时候,上面的状态自动地被类加上了。
class Solution:
def uniquePaths(self, m: int, n: int) -> int:
dp=[1]*n
for i in range(1,m):
for j in range(1,n):
dp[j]+=dp[j-1]
return dp[-1]
2、Leetcode 63:不同路径II
题目描述
解题思路
和上一题思路差不多,只不过对于dp的状态更新要保证点不是障碍物即可
代码实现
#二维矩阵
class Solution:
def uniquePathsWithObstacles(self, obstacleGrid: List[List[int]]) -> int:
#行和列
row=len(obstacleGrid)
col=len(obstacleGrid[0])
#建立dp矩阵
dp=[[0]*col for i in range(row)]
#初始化矩阵的值
for i in range(col):
if obstacleGrid[0][i]==0:
dp[0][i]=1
else:
break
for j in range(row):
if obstacleGrid[j][0]==0:
dp[j][0]=1
else:
break
#开始遍历
for i in range(1,row):
for j in range(1,col):
if obstacleGrid[i][j]!=1:
dp[i][j]=dp[i-1][j]+dp[i][j-1]
return dp[-1][-1]
为了让j可以在边界取到j-1,在每一行的左边加入一个1充当障碍物,所以最后也要返回dp[-2]
class Solution:
def uniquePathsWithObstacles(self, obstacleGrid: List[List[int]]) -> int:
#行和列
row=len(obstacleGrid)
col=len(obstacleGrid[0])
#建立一维dp矩阵
dp=[1]+[0]*col
#开始遍历
for i in range(0,row):
for j in range(0,col):
if obstacleGrid[i][j]:
dp[j]=0
else:
dp[j]+=dp[j-1]
return dp[-2]
3、Leetcode 1143:最长公共子序列
题目描述
- 当前对比的字母相同时: d p [ i ] [ j ] = d p [ i − 1 ] [ j − 1 ] + 1 dp[i][j]=dp[i-1][j-1]+1 dp[i][j]=dp[i−1][j−1]+1
- 不同时: d p [ i ] [ j ] = m a x ( d p [ i − 1 ] [ j ] , d p [ i ] [ j − 1 ] ) dp[i][j]=max(dp[i-1][j],dp[i][j-1]) dp[i][j]=max(dp[i−1][j],dp[i][j−1])
代码实现
class Solution:
def longestCommonSubsequence(self, text1: str, text2: str) -> int:
#判断特殊条件
if not text1 or not text2:
return 0
#两个字符串的长度
m=len(text1)
n=len(text2)
#建立dp矩阵
dp=[[0]*(n+1) for i in range(m+1)]
for i in range(1,m+1):
for j in range(1,n+1):
#如果当前对比的字母是一样的,那么就是i-1和j-1的最长公共子序列+1
if text1[i-1]==text2[j-1]:
dp[i][j]=dp[i-1][j-1]+1
#如果当前对比的字母不相同,那么就是i-1,j或者i,j-1两者之间最长的公共子序列。
else:
dp[i][j]=max(dp[i-1][j],dp[i][j-1])
return dp[-1][-1]
4、Leetcode 70:爬楼梯
重写,不多解释了
代码
class Solution:
def climbStairs(self, n: int) -> int:
dp=[1]+[2]*(n-1)
for i in range(2,n):
dp[i]=dp[i-2]+dp[i-1]
return dp[-1]
5、Leetcode 120:三角形的最小路径和
- 对于三角形两条边上的点,它的值只能是沿着边的上一个状态加自己本身得值得到,而在三角形内的点可以由左上或右上的状态加自己本身的值得到,取最小的值即可。
代码
class Solution:
def minimumTotal(self, triangle: List[List[int]]) -> int:
#建立一个三角形的动态矩阵
n=len(triangle)
dp=[[0]*n for i in range(n)]
#初始化,第一层的值就等于他本身
dp[0][0]=triangle[0][0]
#开始遍历
for i in range(1,n):
#三角形左斜边的值的累加只能来自于边
dp[i][0]=dp[i-1][0]+triangle[i][0]
for j in range(1,i):
#不在三角形边上的值可以来自于左斜上方或者右斜上
dp[i][j]=min(dp[i-1][j-1],dp[i-1][j])+triangle[i][j]
#三角形右斜边的值累加只能来自于边
dp[i][i]=dp[i-1][i-1]+triangle[i][i]
#返回最后一行的最小值
return min(dp[n-1])
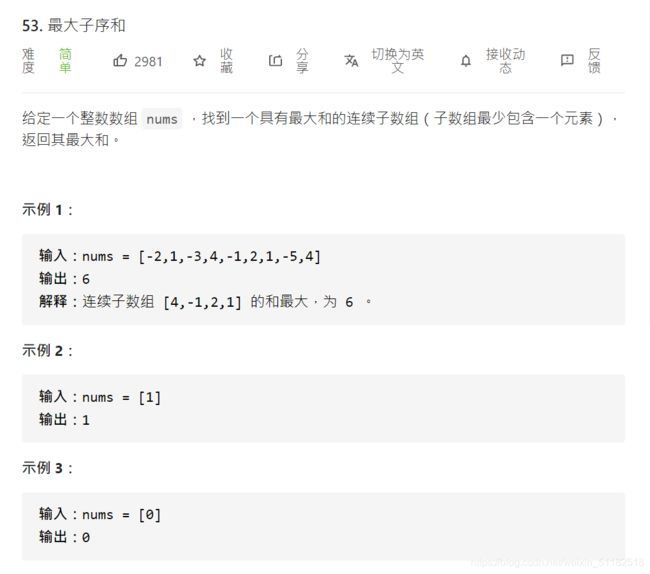
6、Leetcode 55: 最大子序和
题目描述
![]()
解题思路
这道题已经写了很多遍了,就不多说。
代码实现
class Solution:
def maxSubArray(self, nums: List[int]) -> int:
#特殊情况,如果长度为1,输出本身
if len(nums)==1:
return nums[0]
#定义两个变量,一个存储当前的0,i的和,一个存储上一次的
cur=last=nums[0]
#定义一个储存最大值的变量
max_count=nums[0]
#遍历
for i in range(1,len(nums)):
#如果之前的加当前值比当前值还小:
if last+nums[i]<=nums[i]:
#储存的状态变为当前值
cur=nums[i]
else:
cur=last+nums[i]
#对比当前的最大子序和max的关系
if max_count<cur:
#更新
max_count=cur
#更新last
last=cur
#返回最大值
return max_count
7、Leetcode 152:乘积最大子树和
解题思路
因为列表中有负数的存在,如果对于每个位置的遍历只看它子序列中最大的乘积乘以它和它自身的话,是不正确的。对于当前位置为负数,乘以它子序列的最小值,即也为负的情况才是对于当前位置的最大状态。
所以在进行动态规划时,对于每个时刻,它的前面子序列的最大乘积就是在max(i-1),min(i-1)和nums[i]中选择最大的。那么计算min(i-1),就是在max(i-1),min(i-1),和nums[i]中选择最小的。
代码实现
class Solution:
def maxProduct(self, nums: List[int]) -> int:
if not nums:
return 0
#最大值的状态统计
max_pre=nums[0]
#最小值的状态统计
min_pre=nums[0]
#最后输出的值
res=nums[0]
#开始遍历
for i in range(1,len(nums)):
#如果i为正数,那要判断乘不乘当前的值
max_cur=max(max_pre*nums[i],min_pre*nums[i],nums[i])
min_cur=min(max_pre*nums[i],min_pre*nums[i],nums[i])
#更新一下最大值
res=max(max_cur,res)
#移动
max_pre=max_cur
min_pre=min_cur
return res
8、Leetcode 332:零钱兑换问题
解题思路
对于amount+1,遍历一遍coins中的硬币c,它的转移是从amount+1-c这个状态加1得到的。即对于凑11元,coins中有一个5元,3元,和1元,那么可行的方案就是:
- 凑6元+一个五元硬币
- 凑8元+一个三元硬币
- 凑10元+加一个1元硬币
因为都是加了一个硬币,那么就要对比的是凑6、8、10元中需要最小的硬币数。
在代码中多cur代表使用最少的硬币书凑得到的amount,每次要和amount+1对比一下,因为如果cur一直没更新,说明coins中凑不出来amount+1
代码实现
class Solution:
def coinChange(self, coins: List[int], amount: int) -> int:
#建立dp
dp=[0]*(amount+1)
#当前最大值
#开始遍历:
for i in range(1,amount+1):
cur=amount+1
#遍历每个coins
for c in coins:
#如果c比当前target小的话
if c<=i:
cur=min(cur,dp[i-c])
dp[i]=cur+1 if cur <amount+1 else amount+1
return -1 if dp[-1]==amount+1 else dp[-1]
9、Leetcode 198:打家劫舍
题目描述
解题思路
对于长度为0 :i的偷窃方案,只能选择从0 :i-2加上当前的值或者0:i-1的值。
在这里n-1和n-2的状态值是一样的。
代码实现
class Solution:
def rob(self, nums: List[int]) -> int:
if not nums:
return 0
#如果只有一个数
if len(nums)==1:
return nums[0]
#建立dp列表
dp=[0]*len(nums)
#对于只有第一间房,直接偷
dp[0]=nums[0]
#对于只有两间房,偷较大的
dp[1]=max(nums[0],nums[1])
#开始遍历
for i in range(2,len(nums)):
dp[i]=max(dp[i-2]+nums[i],dp[i-1])
return dp[len(nums)-1]
10、Leetcode 121:买卖股票的最佳时机
解题思路
使用dp列表去存储对于0到n每个时刻的利润最大的值。对于每个时刻i,有两种操作:
- 不卖:那它的值等于i-1时刻的值
- 卖:它的值等于当前时刻股票的价格减去前面所有时刻的最低价格
取两种情况较大的值,保存在dp列表中。
代码实现
class Solution:
def maxProfit(self, prices: List[int]) -> int:
n=len(prices)
#特殊条件
if n==0:
return 0
#动态列表
dp=[0]*n
#定义一个存储最低价格的变量
min_price=prices[0]
#开始遍历
for i in range(n):
#找到对于每个时刻前面最低的价格
min_price=min(min_price,prices[i])
#对于每个时刻,要么不抛,要么卖掉,利润为当前价格减去之前的最低价格
dp[i]=max(dp[i-1],prices[i]-min_price)
return dp[-1]
11、Leetcode 122:买入股票的最佳时机II
解题思路
现在是凌晨12:30,写不动了,大致的思路是,对于dp增加一个维度表示当前是否持有股票的状态。分情况讨论
代码实现
class Solution:
def maxProfit(self, prices: List[int]) -> int:
n=len(prices)
dp=[[0]*2for _ in range(n)]
#如果第一天不持有股票,利润为0
dp[0][0]=0
#如果第一天就买入,利润为负
dp[0][1]=-prices[0]
for i in range(1,n):
#如果第i天没持有,可能上一时刻也没有,也可能i-1持有,今天卖掉了
dp[i][0]=max(dp[i-1][0],dp[i-1][1]+prices[i])
#如果第i天持有,可能上一时刻持有,也可能当前买入了
dp[i][1]=max(dp[i-1][1],dp[i-1][0]-prices[i])
#最后时刻持有一定小于不持有
return dp[n-1][0]
12、Leetcode 123:买卖股票的最佳时机III
解题思路
对于在第i天的状态,大概有四个操作:
- 买入了一次
- 买卖一次
- 买卖一次+买入一次
- 买卖两次
状态转移方程:
![]()
初始化的时候,在i=0天的时候,如果是买入一次和两次都是-prices[0],如果是买卖一次和买卖两次,对于第一天,手里的收益为0.
代码实现
class Solution:
def maxProfit(self, prices: List[int]) -> int:
n=len(prices)
#初始化状态
#对于只买入一次和买入两次
buy1=-prices[0]
buy2=-prices[0]
#对于买入卖出一次和两次
sell1,sell2=0,0
#开始循环
for i in range(1,n):
#对于买入一次,可以选择什么都不做,和当前时刻买入
buy1=max(buy1,-prices[i])
#对于买卖一次的,可以选择当前继续持有,也可以选择卖出
sell1=max(sell1,buy1+prices[i])
#对于买入两次,可以选择当前不买入,也可以选择卖过一次后买入
buy2=max(buy2,sell1-prices[i])
#对于买卖两次,可以选择当前继续持有,也可以选择卖出
sell2=max(sell2,buy2+prices[i])
return sell2
13、Leetcode 309:最佳买卖股票时机含冷冻期
解题思路
三个状态:
- 当前时刻持有
对于当前时刻持有,可能是前一天也持有,也可能是前一天未持有但不在冷静期,然后今天买入 - 当前时刻未持有,且在冷静期
如果当前处于冷静期,说明前一天必然进行了卖出,则从前一天持有的状态+prices[i] - 当前时刻未持有,且不在冷静期
第一种为前一天也未持有,不在冷静期,也可能是前一天未持有,但在冷静期。
取n-1时刻最大的值
代码实现
class Solution:
def maxProfit(self, prices: List[int]) -> int:
n=len(prices)
#dp列表
dp=[[0]*3 for i in range(n)]
#状态初始化
dp[0][0]=-prices[0]
dp[0][1],dp[0][2]=0,0
for i in range(1,n):
#对于当前持有股票,可能是一直持有,也可能是在前一天且不在冷静期下当天买入
dp[i][0]=max(dp[i-1][0],dp[i-1][2]-prices[i])
#对于当前未持有,且在冷静期中,说明前一天持有,今天卖出了
dp[i][1]=dp[i-1][0]+prices[i]
#对于当天未持有,且不在冷静期,可能是前一天也未持有,也可能是在前一天处于冷静期
dp[i][2]=max(dp[i-1][2],dp[i-1][1])
return max(dp[n-1][1],dp[n-1][2])
14、Leetcode 188:买卖股票的最佳时机IV
解题思路
将dp列表扩充到二维数组,第二个维度储存完成了第j次交易。
那么对于i时刻当前持有股票的buy来说:
- i-1时刻就已经持有了
- i-1时刻未持有,在当前时刻进行一个买入
对于i时刻当前未持有股票
- i-1时刻未持有
- i-1时刻未持有,交易次数为j-1,当前时刻选择卖出,完成了j笔交易
代码实现
class Solution:
def maxProfit(self, k: int, prices: List[int]) -> int:
if not prices:
return 0
n=len(prices)
#将k的范围缩小
k=min(k,n//2)
#建立dp矩阵
buy=[[0]*(k+1) for _ in range(n)]
sell=[[0]*(k+1) for _ in range(n)]
#初始化buy
buy[0][0]=-prices[0]
for i in range(1,k+1):
buy[0][i]=-99999
sell[0][i]=-99999
#开始循环
for i in range(1,n):
#j=0,不需要考虑sell
buy[i][0]=max(buy[i-1][0],sell[i-1][0]-prices[i])
for j in range(1,k+1):
#对于当前持有,可能是上一个时刻就持有,也可能是上一时刻未持有当前时刻买入
buy[i][j]=max(buy[i-1][j],sell[i-1][j]-prices[i])
#对于当前未持有,可能是上一个时刻未持有,也可能是上一时刻持有,当前时刻卖出,完成了第j笔交易
sell[i][j]=max(sell[i-1][j],buy[i-1][j-1]+prices[i])
#最大利润一定是卖出的
return max(sell[n-1])
15、Leetcode 714:买卖股票的最佳时机含手续费
解题思路
这题与买卖股票的最佳时机ii类似,但多了一个手续费,由于一次买入卖出只交一次手续费,那么选择在卖出时交手续费即可。两种状态:
- 当前时刻持有
- 当前时刻未持有
代码实现
class Solution:
def maxProfit(self, prices: List[int], fee: int) -> int:
n=len(prices)
dp=[[0]*2 for _ in range(n)]
#初始化
#持有股票
dp[0][0]=-prices[0]
#未持有股票
dp[0][1]=0
#开始遍历
for i in range(1,n):
#如果当前时刻持有股票
#可能是上一时刻就持有,也可能是在上一时刻未持有,但这一时刻买入
dp[i][0]=max(dp[i-1][0],dp[i-1][1]-prices[i])
#如果当前时刻未持有,可能是上一时刻未持有或上一时刻持有当前时刻卖出
dp[i][1]=max(dp[i-1][1],dp[i-1][0]+prices[i]-fee)
#最大利润一定是未持有的状态
return dp[n-1][1]
16、Leetcode 32:最长有效括号
代码实现
class Solution:
def longestValidParentheses(self, s: str) -> int:
n=len(s)
if n==0:
return 0
#建立dp
dp=[0]*n
#开始遍历
for i in range(n):
if i>0 and s[i]==")":
if s[i-1]=="(":
dp[i]=dp[i-2]+2
elif s[i-1]==")" and i-dp[i-1]-1>=0 and s[i-dp[i-1]-1]=="(":
dp[i]=dp[i-1]+2+dp[i-dp[i-1]-2]
return max(dp)
17、Leetcode 64:最小路径和
解题思路
这道题的思路其实和之前的不同路径的思路是一样的,只不过在计算中计算的是每一个格子的具体值是多少,因为走法只能是往下走或往右走,所以对于一个不在上边界和左边界的格子,它要么从上面来,要么从左边来,选择两个前状态最小的路径值。对于边界条件的考虑,除了初始点为当前值以外,上边界和左边界的值只能来自左边和上面,对于这两条路径来说,它的值路径值是固定的。
代码实现
class Solution:
def minPathSum(self, grid: List[List[int]]) -> int:
#定义一下矩阵的长宽
row=len(grid)
col=len(grid[0])
#建立dp
dp=[[0]*(col) for _ in range(row)]
dp[0][0]=grid[0][0]
#边际处理
#对于最上层的格子只能横着走
for j in range(1,col):
dp[0][j]=dp[0][j-1]+grid[0][j]
#对于j=0的格子只能往下走
for i in range(1,row):
dp[i][0]=dp[i-1][0]+grid[i][0]
#开始遍历
for i in range(1,row):
for j in range(1,col):
#每一个位置可能是从上面或者左边过来的
dp[i][j]=min(dp[i-1][j],dp[i][j-1])+grid[i][j]
return dp[-1][-1]
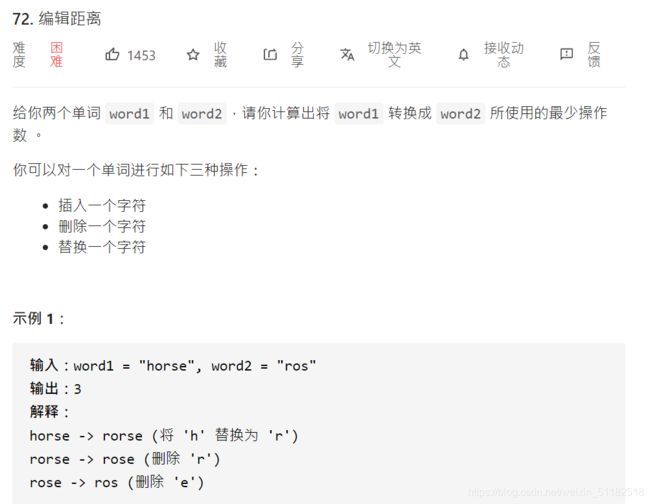
18、Leetcode 72 :编辑距离
题目描述
解题思路
虽然在dp中是困难题,但做过好多遍了,对于当前i和j相等的情况很好分析。当二者不相等时,就是插入、添加和删除三种情况
- 删除:i和j都删除的话,转移为 d p [ i − 1 ] [ j − 1 ] + 1 dp[i-1][j-1]+1 dp[i−1][j−1]+1
- insert,以word1为基准的话,要插入一个才能保证word1和word2相同,那么对于word1的i等于word2的j-1
- 移除,以word2为基准的话,要移除一个才保证word1和word2相同,那么就是 d p [ i − 1 ] [ j ] dp[i-1][j] dp[i−1][j]+1
代码实现
class Solution:
def minDistance(self, word1: str, word2: str) -> int:
#定义两个word的长度
m=len(word1)
n=len(word2)
#建立dp
dp=[[0]*(n+1) for _ in range(m+1)]
#考虑边界条件,如果word1为空,
for i in range(1,n+1):
dp[0][i]=i
#如果word2为空
for j in range(1,m+1):
dp[j][0]=j
#开始遍历
for i in range(1,m+1):
for j in range(1,n+1):
#如果当前字符相同
if word1[i-1]==word2[j-1]:
dp[i][j]=dp[i-1][j-1]
else:
dp[i][j]=min(dp[i-1][j],
dp[i-1][j-1],
dp[i][j-1])+1
return dp[-1][-1]
19、Leetcode 91:解码方法
题目描述
解题思路
对于状态的转移,可以有以下两种情况:
- 对于当前时刻i对应的数字不为0,那么它自己就可以算一种情况,与i-1的状态应该一致,因为目标结果是有多少种解码的方法
- 对于当前时刻的对应的数字,要考虑它和前一位进行组合,如果组合后的数字是在10-26这个区间,那么对于dp[i+1]这个状态它还要加上从dp[i-1]过来的。
代码实现
class Solution:
def numDecodings(self, s: str) -> int:
n=len(s)
if n==0:
return 0
#建立dp状态列表
dp=[0]*(n+1)
#如果第一位是0,无法编译
if s[0]=="0":
return 0
#初始化
dp[0],dp[1]=1,1
#开始遍历
for i in range(1,n):
#只要s[i]不等于0,那么它自身可以编译
if s[i]!="0":
dp[i+1]=dp[i]
#计算i-1和i是否可以组成一个被编译的十位数
nums=10*(ord(s[i-1])-ord("0"))+ord(s[i])-ord("0")
if 10<=nums<=26:
dp[i+1]+=dp[i-1]
return dp[n]
20、Leetcode 221:最大正方形
解题思路
对于 d p [ i ] [ j ] dp[i][j] dp[i][j]的定义是以(i,j)为右底角所能达到的最多的正方形的个数,初始化的限制条件为对于上层和左边的每一个点值为1,那么最多就是1,值为0,则为0。
对于那些在matrix中值为1的点,它的状态转移来自于(i-1,j-1)(i,j-1)(i-1,j)中最小的加1,因为要在三个方向上保证都是正方形,那么要取最小的,否则不满足正方形的边长的限制。由于返回值不一定由最后时刻的dp决定,所以要维护一个变量去在迭代中更新最小值。
代码实现
class Solution:
def maximalSquare(self, matrix: List[List[str]]) -> int:
row=len(matrix)
col=len(matrix[0])
if row==0 or col==0:
return 0
#建立dp
dp=[[0]*col for _ in range(row)]
max_side=0
#开始遍历
for i in range(row):
for j in range(col):
#如果当前为1
if matrix[i][j]=="1":
if i==0 or j==0:
dp[i][j]=1
else:
dp[i][j]=min(dp[i-1][j-1],dp[i-1][j],dp[i][j-1])+1
#更新max_side
max_side=max(max_side,dp[i][j])
return max_side*max_side
21、Leetcode 403:青蛙过河
解题思路
定义 d p [ i ] [ j ] dp[i][j] dp[i][j]为跳跃至i位置,所需要的跳跃数量,j表示上一个位置,True or False
代码中的diff代表上一次跳跃的的单元格的数量,那么当前只能跳跃diff+1,diff或者diff-1的单元格的数量。
代码实现
class Solution:
def canCross(self, stones: List[int]) -> bool:
n = len(stones)
dp = [[False] * n for _ in range(n)]
dp[0][1] = True
for i in range(1, n):
for j in range(i):
diff = stones[i] - stones[j]
# print(i, diff)
if diff < 0 or diff >= n or not dp[j][diff]: continue
dp[i][diff] = True
if diff - 1 >= 0: dp[i][diff - 1] = True
if diff + 1 < n: dp[i][diff + 1] = True
return any(dp[-1])
22、Leetcode 410:分割数组的最大值
解题思路
d p [ i ] [ j ] dp[i][j] dp[i][j]代表对于第i个位置分成j段后每种情况下每段的最大值的最小值。
那么状态的转移可以定义为
假设在0-i区间第j段分为k:i,那么转移的就是 d p [ k ] [ j − 1 ] dp[k][j-1] dp[k][j−1]和i-k区间所有元素加和的最大值,对于每种k
这里的代码应该是没错的,但超时了好烦,,,,
代码实现
class Solution:
def splitArray(self, nums: List[int], m: int) -> int:
#nums的长度
n=len(nums)
#建立dp,表示前i个数中可分为j段
dp=[[10**18]*(m+1) for _ in range(n+1)]
#初始化
dp[0][0]=0
#定义一个列表,每个位置是之前的nums的累加
sub=[0]
for num in nums:
sub.append(sub[-1]+num)
#开始循环
for i in range(1,n+1):
#j的范围不能超过m也不能超过i
for j in range(1,min(i,m)+1):
#所有可能的分割情况:0-k,k-i
for k in range(i):
#当前分段后的最大值应该是前k个数分为j-1段的和或者第j段的和中的最大值中的最小值
dp[i][j]=min(dp[i][j],max(dp[k][j-1],sub[i]-sub[k]))
return dp[n][m]
23、Leetcode 552:学生出勤记录II
题目描述
解题思路
d p [ i ] [ j ] [ k ] dp[i][j][k] dp[i][j][k]中i表示出勤的长度,j表示A的个数,K表示末尾连续的L的个数。
根据题目要求,A不得超过1,K不得超过2
1、初始化状态的分析,如果长度为1,那么只能是A,P,L的其中一个。
- 出勤为p: d p [ 1 ] [ 0 ] [ 0 ] = 1 dp[1][0][0]=1 dp[1][0][0]=1
- 出勤为A d p [ 1 ] [ 1 ] [ 0 ] = 1 dp[1][1][0]=1 dp[1][1][0]=1
- 出勤为L: d p [ 1 ] [ 0 ] [ 1 ] = 1 dp[1][0][1]=1 dp[1][0][1]=1
2、当出现连续的k时,且k不超过2,那么把这些k删掉的状态转移是相同的
d p [ i ] [ j ] [ k ] = d p [ i − 1 ] [ j ] [ k − 1 ] dp[i][j][k]=dp[i-1][j][k-1] dp[i][j][k]=dp[i−1][j][k−1]
3、如果末尾没有L,当没有A时,末尾的为P,那么可以删掉也不影响,删掉p,可能末尾是一个L,两个L或者0个L
d p [ i ] [ 0 ] [ 0 ] = d p [ i − 1 ] [ 0 ] dp[i][0][0]=dp[i-1][0] dp[i][0][0]=dp[i−1][0]
4、当末尾没有L,但却是A时,那么吧i位置的A删掉与情况3相同。
代码实现
class Solution:
def checkRecord(self, n: int) -> int:
mod=pow(10,9)+7
# 长度、'A'出现的次数、末尾连续'L'的次数
dp=[[[0]*3 for _ in range(2)]for _ in range(n+1)]
# base case:长度为1,那么是'A'、'L'、'P'中的一种
dp[1][1][0]=1 #A
dp[1][0][1]=1 #L
dp[1][0][0]=1 #P
for i in range(2,n+1):
# 若末尾是k个连续的L(即k>0)
for j in range(2):
for k in range(1,3):
dp[i][j][k]=dp[i-1][j][k-1]%mod
# 若末尾没有L(即k=0)
dp[i][0][0]=noA=sum(dp[i-1][0])%mod
dp[i][1][0]=noA+sum(dp[i-1][1])%mod
# 结果等于dp[n]的每种可能
return sum(sum(col) for col in dp[-1])%mod
24、Leetcode 647:回文子串
题目描述
解题思路
使用 d p [ i ] [ j ] dp[i][j] dp[i][j]表示对于字符串s,从i到j位置是否是回文串,由于每个子串都要计数,那么只要 d p [ i ] [ j ] = 1 dp[i][j]=1 dp[i][j]=1时就count+1,对于每个字符本身,肯定是回文串,所以count+1,对于不相连得位置,如果它们对应元素相等,且它们距离小于2说明它们是连续的,那么也为1,如果距离大于2,就要看i和j中间的字符是不是回文串了。对于每个为1得dp位置,count+1。最后返回count的值。
代码实现
class Solution:
def countSubstrings(self, s: str) -> int:
n=len(s)
#建立dp,表示i到j位置有多少个回文数
dp=[[0]*n for _ in range(n)]
count=0
#开始循环
for i in range(n-1,-1,-1):
#自身肯定是回文数
dp[i][i]=1
count+=1
for j in range(i+1,n):
#如果i和j对应的相同
if s[i]==s[j]:
#只有两个数的前提下
if j-i<=2:
dp[i][j]=1
else:
dp[i][j]=dp[i+1][j-1]
if dp[i][j]:
count+=1
return count
25、Leetcode 76:最小覆盖子串
题目描述
解题思路
这题做了挺久的,第一次做滑动窗口的题,直接上解题思路吧,复习的时候再回来完善自己的思路。

代码实现
class Solution:
def minWindow(self, s: str, t: str) -> str:
#建立一个空字典储存t中的元素和需要的个数
need=collections.defaultdict(int)
#遍历t,将t存储进去
for char in t:
need[char]+=1
#统计滑动窗口需要找到的数量
count=len(t)
res=(0,float("inf"))
#滑动窗口的起始点
i=0
#开始遍历s
for j,c in enumerate(s):
#如果当前c出现在t中,将count-1
if need[c]>0:
count-=1
#如果没出现,把c添加到need,并-1,为了i增加时可以把包括的在抛出出去
need[c]-=1
#当count已经为0时,代表当前窗口已经包含了所有的t中元素,那么要将i扩大
if count==0:
#让i扩大,直到s[i]找到t中的元素
while True:
c=s[i]
#找到了
if need[c]==0:
break
#没找到的话,把原先那些-1的值加回来
need[c]+=1
#移动i
i+=1
#当前i,j为第一次找到的最小字串区间,对比更新
if j-i<res[1]-res[0]:
#更新
res=(i,j)
#将i移动一个,重新寻找一个滑动窗口
#先要把need中的属于t的元素加一个1
need[s[i]]+=1
#将count+1
count+=1
#移动i
i+=1
#返回时如果j大于了长度,那么说明没找到合适的窗口
return ""if res[1]>len(s) else s[res[0]:res[1]+1]
26、Leetcode 312:戳气球
解题思路

对于i,j区间内的所有可能的数字k,它可以和i,j组成一个戳爆气球后的硬币组合,对于每个位置k,它的硬币总数为val[i]*val[k]*val[j]再加上 d p [ i ] [ k ] + d p [ k ] [ j ] dp[i][k]+dp[k][j] dp[i][k]+dp[k][j]的值,找到最大的位置k,并存储在 d p [ i ] [ j ] dp[i][j] dp[i][j]中。
代码实现
class Solution:
def maxCoins(self, nums: List[int]) -> int:
#长度
n=len(nums)
#建立dp
dp=[[0]*(n+2) for _ in range(n+2)]
#nums的扩充
val=[1]+nums+[1]
#开始遍历
for i in range(n-1,-1,-1):
for j in range(i+2,n+2):
for k in range(i+1,j):
total=val[i]*val[k]*val[j]
total+=dp[i][k]+dp[k][j]
dp[i][j]=max(total,dp[i][j])
return dp[0][n+1]
27、Leetcode 213:打家劫舍ii
题目描述

解题思路
与第九题的状态转移是一样的概念,但是加入了环以后,第一个和最后一个连接到了一起,表示第一个和最后一个不可能同时偷盗,故将列表刨除第一个和最后一个分开讨论,取到最大值。
代码实现
class Solution:
def rob(self, nums: List[int]) -> int:
if len(nums)==1:
return nums[0]
def Dp(nums):
n=len(nums)
if not nums:
return 0
if n==1:
return nums[0]
dp=[0]*(n)
dp[0]=nums[0]
#初始化
dp[1]=max(nums[0],nums[1])
for i in range(2,n):
dp[i]=max(dp[i-2]+nums[i],dp[i-1])
return dp[n-1]
p1=Dp(nums[1:])
p2=Dp(nums[:-1])
return max(p1,p2)
28、Leetcode 300:最长递增子序列
题目描述
解题思路
维护一个dp列表,对于当前位置的元素,找到前面元素比它小的值,找到所有比它小的值的dp状态最大的那个加1,就是当前位置元素的最长子序列的值。
代码
class Solution:
def lengthOfLIS(self, nums: List[int]) -> int:
if len(nums)<=1:
return len(nums)
dp=[1 for i in range(len(nums))]
for j in range(1,len(nums)):
for k in range(0,j):
if nums[k]<nums[j]:
dp[j]=max(dp[j],dp[k]+1)
return max(dp)
29、Leetcode 53:最大子序列和
解题思路
核心思路是,只要前面的数相加的和不小于0那么就可以继续加下一个数,如果前面的数相加小于0的话就选择当前的数作为cur的值。还要定义一个max_count的变量,如果cur大于了max_count就更新cur。因为存在加上这个数虽然不小于0但是却变小了的可能。
代码
class Solution:
def maxSubArray(self, nums: List[int]) -> int:
if len(nums)==1:
return nums[0]
count=-10**10
cur=last=0
for i in range(0,len(nums)):
if last+nums[i]>nums[i]:
cur=last+nums[i]
else:
cur=nums[i]
if cur > count:
count=cur
last=cur
return count
30、Leetcode 72:编辑距离计算
class Solution:
def minDistance(self, word1: str, word2: str) -> int:
n=len(word1)
m=len(word2)
dp=[[0 for x in range(m+1)] for x in range(n+1)]
for i in range(n+1):
dp[i][0]=i
for j in range(m+1):
dp[0][j]=j
for i in range(1,n+1):
for j in range(1,m+1):
if word1[i-1] == word2[j-1]:
dp[i][j]=dp[i-1][j-1]
else:
dp[i][j]=1+min(dp[i-1][j],
dp[i][j-1],
dp[i-1][j-1])
return dp[n][m]
31、Leetcode 332:零钱兑换
代码
class Solution:
def coinChange(self, coins: List[int], amount: int) -> int:
mems=[0 for _ in range(amount+1)]
for i in range(1,amount+1):
cur=amount+1
for j in coins:
if j<=i:
cur=min(cur,mems[i-j])
mems[i]=cur+1 if cur < amount+1 else amount+1
return -1 if mems[-1]== amount+1 else mems[-1]
32、Leetcode 494:目标和
题目描述

解题思路
一种0/1背包问题,dp表示前i个数和为方案j的方案数,对于每个时刻的i,它的转移矩阵可以是加或减当前i位置元素的值。相加和的范围应该是从-sums 到+sums这个区间。最后只需要返回最后一个i位置的时候,total+s的方案数即可(因为是从负区间到正区间)。除此之外,对于每个时刻对于加nums[i],要保证加完不超过上界。减去nums[i]要保证不超过下界。附上leetcode的解释:

代码
class Solution:
def findTargetSumWays(self, nums: List[int], S: int) -> int:
total=sum(nums)
#如果nums所有相加都比S小,说明无法凑出s
if abs(total)<abs(S):
return 0
#建立dp矩阵,i,j表示0~i个元素加和为j的方法。
dp=[[0 for j in range(total*2+1)]for i in range(len(nums))]
#初始化
if nums[0]==0:
dp[0][total]=2
else:
dp[0][total-nums[0]]=1
dp[0][total+nums[0]]=1
for i in range(1,len(nums)):
for j in range(total*2+1):
l=j-nums[i] if j-nums[i]>=0 else 0
r=j+nums[i] if j +nums[i]<total*2+1 else 0
dp[i][j]=dp[i-1][l]+dp[i-1][r]
return dp[-1][total+S]
总结
做完了课程中所有的dp题,对于做出dp题最重要的三点:
- 1、找到转移方程即最优子问题
- 2、确定边际条件
- 3、维护的dp的长度
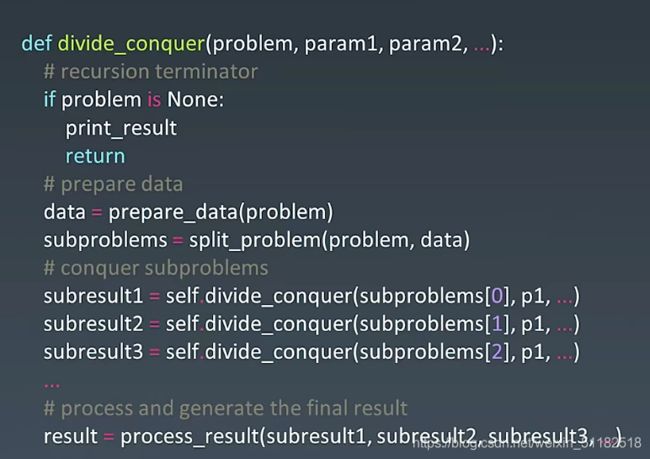
第六章 分治、回溯
分治代码模板
- 把问题拆成子问题
- 把子问题的结果进行拼接
回溯
1、Leetcode 50:Pow(x,n)
题目描述
解题思路
核心思想为将n次幂对2取整,通过递归将每次x的二分之n次幂进行相乘。如果是奇数还需要乘以一个x本身。
代码
class Solution:
def myPow(self, x: float, n: int) -> float:
def split_(N):
if N==0:
return 1.0
y=split_(N//2)
return y*y if N%2==0 else y*y*x
return split_(n) if n>=0 else 1.0/split_(-n)
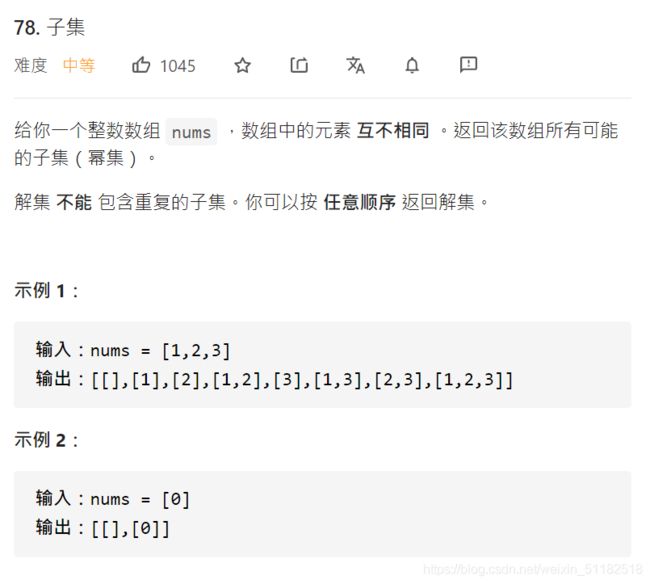
2、Leetcode 78:子集
代码
class Solution:
def subsets(self, nums: List[int]) -> List[List[int]]:
res = []
n = len(nums)
def helper(i, tmp):
res.append(tmp)
for j in range(i, n):
helper(j + 1,tmp + [nums[j]] )
helper(0, [])
return res
迭代思想的代码
class Solution:
def subsets(self, nums: List[int]) -> List[List[int]]:
res = [[]]
for i in nums:
res = res + [[i] + num for num in res]
return res
3、Leetcode 169:多数元素
代码
Approach 1:
直接使用collections中的counter建立字典,key为列表的每个元素,value为列表中每一个数字出现的次数。直接返回value最大的key即可。
class Solution:
def majorityElement(self, nums: List[int]) -> int:
d=collections.Counter(nums)
return max(d.keys(),key=d.get)
Approach 2: 分治
核心思路是如果一个数a是列表中的众数,那么它必定是左右列表中的其中一个子列表或两个子列表的众数。如果a同时是两个列表的众数,那么直接返回这个值即可。如果a只是其中一个列表的众数,那么需要对比左右两个子列表的众数的个数的大小,多的那个为整个列表的众数。
- 终止条件:左==右索引
- 循环点:mid
- 判断条件:
1、如果左众数等于右众数,返回任意一个
2、如果不等,统计窗口范围内的左众数个数和右众数个数,返回大的。
class Solution:
def majorityElement(self, nums: List[int]) -> int:
def dfs(low,high):
if low==high:
return nums[low]
mid=(low+high)//2
left=dfs(low,mid)
right=dfs(mid+1,high)
if left==right:
return left
left_c=sum(1 for i in range(low,high+1)if nums[i]==left)
right_count=sum(1 for i in range(low,high+1) if nums[i]==right)
return left if left_c>right_count else right
return dfs(0,len(nums)-1)
4、Leetcode 17:电话号码的字母组合
解题思路
- 建立一个字典储存每个数字所对应的字母的可能
- 终止条件:如果遍历个数等于给定数字的个数,停止,将ans中添入temp(存储可能的字母)并返回。
- 递归:对于第一位,遍历所有可能的字母,添加一位,对第二位进行递归
- 对于每次递归返回的值,要清除上一层循环的值。
代码
class Solution:
def letterCombinations(self, digits: str) -> List[str]:
m={"2":"abc","3":"def","4":"ghi","5":"jkl","6":"mno","7":"pqrs",
"8":"tuv","9":"wxyz"}
def dfs(i,digits):
#终止条件:
if i ==len(digits):
res.append("".join(temp))
return
for j in m[digits[i]]:
temp.append(j)
#递归下一位
dfs(i+1,digits)
temp.pop()
if not digits:
return []
res=[]
temp=[]
dfs(0,digits)
return res
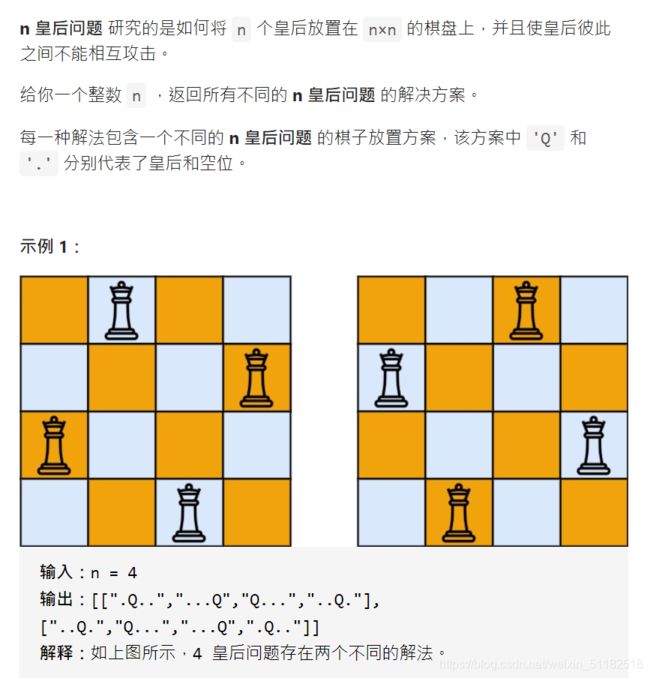
5、Leetcode 51:N皇后问题
解题思路
首先在递归前,需要定义一个col,一个pie,一个na的三个集合,储存的是对于上一层的放置位置,下一层不能放的位置。
-
终止条件:行数等于n的时候,结束,储存结果的列表中把每一个皇后的位置信息添加。
-
对于每一行,需要遍历每一个列,只要这个位置不在col,pie和na中就可以防止,然后将当前行列位置的col,pie,na信息加入到上述集合中。
-
然后就是递归,对于行+1进行递归,此时要更新一下[col]的位置。
-
递归结束后,还是要对上述三个集合进行清除。使用remove函数
-
最后就是定义一个生成棋盘格的函数,因为cur_state中存储的是每一行,皇后所出的列位置i,那么生成棋盘的过程就是遍历每一行,前面加入i个"."后面加上(n-i-1)个“.”。此时board存储的是每一种可能的n行的信息,所以返回的时候要遍历board 步长为n进行添加。
代码
class Solution:
def solveNQueens(self, n: int) -> List[List[str]]:
#特殊情况:
if n<1:
return []
result=[]#储存结果
cols=set()#储存不能放置的列信息
pie=set()#储存不能放置的pie方向信息
na=set()#储存不能放置的na方向信息
#定义函数
def dfs(n,row,cur_state):#row:每一行,cur_state:存储皇后位置
#终止条件:
if row==n:
result.append(cur_state)
#遍历每一行:
for col in range(n):
#如果是在不可以放置的位置,跳过
if col in cols or col+row in pie or row-col in na:
continue
#添加位置信息
cols.add(col)
pie.add(col+row)
na.add(row-col)
#进行递归,对于下一层递归,且更新一下状态
dfs(n,row+1,cur_state+[col])
#清除状态
cols.remove(col)
pie.remove(col+row)
na.remove(row-col)
#定义生成表格的函数:
def generate_result(n):
board=[]
#result存储的是所有的可能的数m*n个
for res in result:
#res中是n行的信息,i是皇后所在位置的列索引
for i in res:
board.append("."*i+"Q"+"."*(n-i-1))
#生成的过程
return [board[i:i+n] for i in range(0,len(board),n)]
dfs(n,0,[])
return generate_result(n)
第七章 深度优先搜索和广度优先搜索
深度优先搜索格式

如果树的每个节点有超过两个子节点:

广度优先搜索格式
1、Leetcode 102:二叉树的层序遍历
代码
class Solution:
def levelOrder(self, root: TreeNode) -> List[List[int]]:
res=[]
queue=collections.deque()
queue.append(root)
while queue:
list1=[]
for i in range(len(queue)):
node=queue.popleft()
if not node:
continue
list1.append(node.val)
queue.append(node.left)
queue.append(node.right)
if list1:
res.append(list1)
return res
2、Leetcode 433:最小基因变化
解题思路
参考了官方的python题解,具体思想分为大概三层:
- 第一层:维护一个队列,格式是(word,step),word代表每次更新一次的字符串,step代表从start开始到达当前word使用的步数
- 第二层:遍历一遍start的每个字符串位置,对于每个位置的元素进行一次替代,对于A,可以替代的有CGT,对于G,可以替代的有ACT,完成一次替代后,可以将替代后的字符串与bank中的做对比,如果替换后的在bank中,把这个字符串更新到队列中,且队列的step+1
- 第三层:不断的从queue里取出word,当word与end的字符串相同,即更新完毕,输出当前word对应的step。
代码
class Solution:
def minMutation(self, start: str, end: str, bank: List[str]) -> int:
#建立一个对应的字典
dic1={
"A":"CGT",
"G":"ACT",
"T":"AGC",
"C":"AGT"
}
queue=[(start,0)]
while queue:
word,step=queue.pop(0)
#终止条件:
if word==end:
return step
#遍历word的每一个元素位置:
for i, k in enumerate(word):
#每个位置都可以由除了当前字母以外的其他三个字母替代
for p in dic1[k]:
#生成一次替换后的word
temp=word[:i]+p+word[i+1:]
#判断temp是否在bank中:
if temp in bank:
#把这个移除避免重复计数:
bank.remove(temp)
#如果在的话可以把它添加到queue中
queue.append((temp,step+1))
#如果循环完整个queue还没有得到step结果,return -1
return -1
3、Leetcode 22: 括号生成问题重写
代码
class Solution:
def generateParenthesis(self, n: int) -> List[str]:
res=[]
def dfs(left,right,s):
#终止条件:
if left == n and right == n:
res.append("".join(s))
return
#left的条件:
if left<n:
s.append("(")
#递归
dfs(left+1,right,s)
s.pop()
if left>right:
s.append(")")
#递归
dfs(left,right+1,s)
s.pop()
dfs(0,0,[])
return res
4、Leetcode 515:在每个树行中找最大值
解题思路
因为在二叉树的层序遍历中,对于每一层是使用列表存储元素,那么只需要在最后将每一层的元素找到最大的并返回即可。
代码
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def largestValues(self, root: TreeNode) -> List[int]:
#建立一个队列实现广度遍历
queue=collections.deque()
#先将root添加进去
queue.append(root)
#建立一个空列表存储答案
res=[]
#进行循环
while queue:
#建立另外一个空列表存储每个每一层的元素
value=[]
#遍历每一层的节点个数:
for i in range(len(queue)):
#将节点取出来
node=queue.popleft()
#如果不是node
if not node:
continue
#将node的值添加到value中
value.append(node.val)
#将node的左右子节点添加到queue里
queue.append(node.left)
queue.append(node.right)
#结束了每一层的循环后找到当前层的最大值
if value:
a=max(value)
#添加到res中
res.append(a)
return res
5、Leetcode 127:单词接龙
解题思路
解题过程:
- 第一步:定义一个添加单词的函数,wordid作为一个词典,把每个词进行编号
- 第二步:定义一个添加边界的函数,对于一个词的每一次字母,替换成"*"然后产生出边界词,把边界词添加到wordid中。除此之外,还要建立一个新的字典,字典的key是原始词,value是所有的边界词,列表形式保存。注意:每次替换后要替换回来供下次循环使用。
- 遍历wordlist中的词,编号。对beginword编号,此时,如果endword不在wordid中,返回0
- 建立两个列表分别存储从beginWord出发的词和endWord出发的词每次走的step。
- 建立两个队列存储两个词走的路线。
- 对于每个内层的循环,终止条件是当前的元素在列表中的值不为“inf”,即为找到了这个词。相当于从两边寻找碰面了。
- 对于每个内层循环,调用edge字典,对于每个词掉入它的所有边界词的可能。
代码实现
class Solution:
def ladderLength(self, beginWord: str, endWord: str, wordList: List[str]) -> int:
def addWord(word:str):
#定义一个函数对所有的wordlist里面的词进行编号,包括边界词
if word not in wordId:
nonlocal nodeNum
wordId[word]=nodeNum
nodeNum+=1
def addEdge(word:str):
#先要addword
addWord(word)
#拿出当前词对应的id
id1=wordId[word]
#列表化
chars=list(word)
for i in range(len(chars)):
tmp=chars[i]
chars[i]="*"
#生成新的word
newWord="".join(chars)
#将newWord添加到字典中
addWord(newWord)
#拿到newWord的id
id2=wordId[newWord]
#将id2添加到id1的key下,将id1添加到id2的key下
edge[id1].append(id2)
edge[id2].append(id1)
#复原
chars[i]=tmp
wordId=dict()
edge=collections.defaultdict(list)
nodeNum=0
#将wordlist的词添加到wordid中编号,并生成边界词
for word in wordList:
addEdge(word)
#将beginword也添加进去
addEdge(beginWord)
#判断endWord在不在里面
if endWord not in wordId:
return 0
#建立从beginWord出发的存储列表
disBegin=[float("inf")]*nodeNum
#获取beginWord的id
beginId=wordId[beginWord]
#初始化
disBegin[beginId]=0
#建立一个队列
queue1=collections.deque([beginId])
#同理,建立从endWord出发的存储列表
disEnd=[float("inf")]*nodeNum
endId=wordId[endWord]
#初始化
disEnd[endId]=0
#建立队列
queue2=collections.deque([endId])
#开始对两个队列进行循环
while queue1 or queue2:
#先从beginword开始走
m=len(queue1)
for i in range(m):
#拿出第一个词
nodeBegin=queue1.popleft()
#终止条件
if disEnd[nodeBegin]!=float("inf"):
#返回一半的路程
return (disBegin[nodeBegin]+disEnd[nodeBegin])//2+1
#对于nodeBegin中所有的边际词进行遍历
for it in edge[nodeBegin]:
#边际词到原始词的操作加1
if disBegin[it]==float("inf"):
disBegin[it]=disBegin[nodeBegin]+1
#把每个边际词压入队列
queue1.append(it)
for j in range(len(queue2)):
nodeEnd=queue2.popleft()
#终止条件
if disBegin[nodeEnd]!=float("inf"):
return (disEnd[nodeEnd]+disBegin[nodeEnd])//2+1
#遍历end开始的每个生成的边际词:
for it in edge[nodeEnd]:
if disEnd[it]==float("inf"):
disEnd[it]=disEnd[nodeEnd]+1
queue2.append(it)
return 0
6、Leetcode 200:岛屿数量
题目描述
解题思路
- 使用深度优先搜索,对于值为1的点,则作为起始节点进行深度优先搜索,在深度优先搜索的过程中,每个搜索到的1都会被标记为0. 最后岛屿的数量就是进行深度优先搜索的次数。
- 第一步,定义一个dfs函数,输入grid,横坐标和纵坐标,记录。遍历这个点上下左右的鸽子,如果坐标值为1,则对这个点进行递归。
- 第二部主函数,遍历每个格子点,nc为多少列,nr为多少行,如果值为1,岛屿树加1,继续进行递归搜索
- 最后return 岛屿数。
这题感觉难度还好,主要点在于对于四个方向的坐标的限制条件以及需要把遍历过的变成0,防止重复遍历,还有一点就是建立一个变量nums去维护岛屿数量。
代码
class Solution:
def dfs(self,grid,r,c):
#先把这个点变为0
grid[r][c]=0
nr=len(grid)
nc=len(grid[0])
#讨论上下左右四种情况:
for x,y in [(r+1,c),(r-1,c),(r,c+1),(r,c-1)]:
if 0<=x<nr and 0<=y<nc and grid[x][y]=="1":
#如果它的上下左右还是为1:
self.dfs(grid,x,y)
def numIslands(self, grid: List[List[str]]) -> int:
nc=len(grid[0])
nr=len(grid)
if nr==0:
return 0
#定义一个岛屿数量
nums=0
#开始遍历
for i in range(nr):
for j in range(nc):
#当遇到为1时
if grid[i][j]=="1":
nums+=1
#继续递归
self.dfs(grid,i,j)
return nums
第八章 :贪心搜索
1、Leetcode 455:分发饼干
题目描述
解题思路
采样贪心算法,先对孩子的胃口进行排序,再对饼干的大小进行排序。定义两个指针分别指向两个列表的首端,那么会有两种情况
- 当前饼干大小可以满足孩子的胃口,两个指针都加1,计数器加一
- 当前饼干无法满足孩子的胃口,饼干指针加1,继续对比
代码
class Solution:
def findContentChildren(self, g: List[int], s: List[int]) -> int:
g.sort()
s.sort()
l=0
r=0
num=0
while l<len(g) and r<len(s):
if g[l]<=s[r]:
num+=1
l+=1
r+=1
else:
r+=1
return num
2、Leetcode 122:买卖股票的最佳时机 II
解题思路
还是使用贪心,只要前一天的价格比后一天低,就可以完成一次买卖。
代码
class Solution:
def maxProfit(self, prices: List[int]) -> int:
n=len(prices)
max_profit=0
for i in range(0,n-1):
if prices[i]<prices[i+1]:
max_profit+=prices[i+1]-prices[i]
return max_profit
3、Leetcode 55:跳跃游戏
题目描述
代码
Approach 1
nums中的每个数字代表可以由该点走到的最大路径,路径为nums的位置索引。初始化的最远距离索引是第一个值2,遍历nums,当索引小于当前最远距离时,可以更新最远距离。如果最后的最远距离大于了nums长度,表示可以达到。
class Solution:
def canJump(self, nums: List[int]) -> bool:
#如果nums中没有0一定可以达到
if 0 not in nums:
return True
#如果长度为1也可以到达
if len(nums)<2:
return True
#定义一个最远距离
max_dis=nums[0]
#遍历
for i in range(1,len(nums)-1):
if i<=max_dis:
max_dis=max(max_dis,i+nums[i])#更新最远坐标
else:
break
return max_dis>=len(nums)-1
Approach 2 DP算法 会超时
class Solution:
def canJump(self, nums: List[int]) -> bool:
dp=[False]*len(nums)
dp[0]=True
for i in range(1,len(nums)):
for j in range(0,i):
if dp[j] and nums[j]>=i-j:
dp[i]=True
break
return dp[-1]
4、Leetcode 860:柠檬水找零
题目描述
解题思路
- 定义两个变量存储5,10元的个数
- 遇到5元,直接收下
- 遇到十元,收下且要保证有一个5元找零
- 遇到20元,优先选择10元的给,再给一个5元,如果没有十元,要保证至少有三个五元。
代码实现
class Solution:
def lemonadeChange(self, bills: List[int]) -> bool:
#建立两个变量储存5元和10元的数量
fives,tens=0,0
#遍历bills
for money in bills:
#如果是5元
if money==5:
fives+=1
elif money==10:
#如果有5元,可以继续
if fives>0:
tens+=1
fives-=1
else:
return False
#如果是20元
else:
#优先使用10元,只要至少有一个十元,只要一个5元,20就能找开
if tens>=1 and fives>=1:
tens-=1
fives-=1
#如果没有十元,那至少要有三个5元
elif tens==0 and fives>=3:
fives-=3
else:
return False
return True
5、Leetcode 874: 模拟行走机器人
题目描述
解题思路
- 定义x,y点为机器人行走的位置,d为机器人的方向
- 使用集合储存障碍物的坐标
- 定义d_x和d_y表示方向,右转向右更新,左转向左更新
- 遍历列表的元素,如果是-2左转,-1右转。
- 对于路径的元素,要一步一步走,判断每一步是否前面会遇到障碍物,每走一步更新一次计算欧氏距离的变量,选择最大的在遍历结束后输出。
代码
class Solution:
def robotSim(self, commands: List[int], obstacles: List[List[int]]) -> int:
#定义坐标值和方向索引
x,y,d=0,0,0
d_x=[0,1,0,-1]
d_y=[1,0,-1,0]
#储存障碍物的坐标,以集合存储
ob=set(map(tuple,obstacles))
res=0
for order in commands:
#如果向右转90度,顺时针更新
if order==-1:
d=(d+1)%4
#如果向左转90度,逆时针更新
elif order==-2:
d=(d-1)%4
else:
#下一个点不能是障碍物
for i in range(order):
if (x+d_x[d],y+d_y[d]) not in ob:
x+=d_x[d]
y+=d_y[d]
res=max(res,x**2+y**2)
return res
6、Leetcode 42: 跳跃游戏II
解题思路,复制自官方答案
代码实现
class Solution:
def jump(self, nums: List[int]) -> int:
#每次可达到的最远距离
max_dis=0
#统计跳跃次数
step=0
#每一个位置的可以达到的最大的点
end=0
#长度
n=len(nums)
#遍历列表
for i in range(n-1):
#只要i在最远距离的范围内
if max_dis>=i:
#根据当前位置的索引更新max_dis
max_dis=max(max_dis,i+nums[i])
if i==end:
end=max_dis
step+=1
return step
第九章 二分查找
三大特性
- 单调性
- 上下界
- 索引访问
代码模板
1、Leetcode 69:x的平方根
代码实现
Approach 1:二分查找
class Solution:
def mySqrt(self, x: int) -> int:
#规定左右边界,x的平方根一定小于x
left,right=0,x
ans=0
#循环
while left<=right:
#计算中间值
mid=(left+right)//2
#如果mid大于目标值,左边查找
if mid*mid > x:
right=mid-1
#如果小于目标值,右边查找
else:
ans=mid
left=mid+1
return ans
Approach 2: 牛顿迭代法
class Solution:
def mySqrt(self, x: int) -> int:
if x==0:
return 0
z=float(x)
while True:
r=0.5*(z+float(x)/z)
if abs(r-z)<1e-6:
break
z=r
return int(z)
2、Leetcode 33:搜索旋转排序数组
解题思路
- 二分查找
- 通过比较nums[0]和nums[mid]的大小判断哪个区间属于有序数组
- 不断更新上下界
代码实现
class Solution:
def search(self, nums: List[int], target: int) -> int:
if not nums:
return -1
#定义左右指针
left,right=0,len(nums)-1
while left<=right:
mid=(left+right)//2
#终止条件
if nums[mid]==target:
return mid
#判断0,mid是否是有序区间
if nums[0]<=nums[mid]:
#判断target的范围
if nums[0]<=target<nums[mid]:
right=mid-1
else:
left=mid+1
else:
if nums[mid]<target<=nums[-1]:
left=mid+1
else:
right=mid-1
return -1
3、Leetcode 367:有效的完全平方数
解题思路
这道题和第一题解法相同,只不过判断条件不同,因为第一题对于无法开平方的数返回的是整数部分,那么只要在结尾判断整数部分的平方和原始的num相等不相等即可。
代码实现
class Solution:
def isPerfectSquare(self, num: int) -> bool:
#二分查找,先定义左右边界
left,right=0,num
#循环条件
ans=0
while left<=right:
#找到mid值
mid=(left+right)//2
#如果mid二次方大于num更新右边界
if mid*mid>num:
right=mid-1
else:
#先更新一下ans
ans=mid
left=mid+1
#判断ans的平方和num是不是相同即可
return ans*ans==num
4、Leetcode 74:搜索二维矩阵
题目描述
解题思路
做出这道题这需要弄清三点即可
- 第一点,使用二分查找
- 第二点,把二维矩阵摊开可以变成一个0,m*n-1的列表
- 第三点,每次定位到的中间值mid,mid//n为行位置,mid%n为列位置,即可找到中间值的具体值。
代码实现
class Solution:
def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
if len(matrix)==0:
return False
#统计行和列的个数
row,col=len(matrix),len(matrix[0])
#左右指针
left,right=0,row*col-1
while left<=right:
#找到中间位置索引:
mid=(left+right)//2
#找到中间值
mid_value=matrix[mid//col][mid%col]
#判断中间值和目标值间的关系
if mid_value>target:
#更新右边界
right=mid-1
elif mid_value<target:
#更新左边界
left=mid+1
else:
return True
#没找到:
return False
5、Leetcode 153:寻找旋转排序数组中的最小值
题目描述
解题思路
- 第一点:如果nums[mid]大于nums[0],有序区间在左边,无序在右边
- 第二点:最小值的点为旋转的点
- 第三点,在无序区间内,如果mid的值大于下一个,下一个为旋转点,如果mid的值小于上一个,mid本身为旋转点。
代码实现
class Solution:
def findMin(self, nums: List[int]) -> int:
#特殊条件1:如果nums只有一个元素
if len(nums)==1:
return nums[0]
#特殊条件2:如果没有进行旋转
if nums[0]<nums[-1]:
return nums[0]
#左右边界
left=0
right=len(nums)-1
#循环
while left <=right:
#中间值
mid=(left+right)//2
#如果上一个值大于mid,mid为变化点
if nums[mid-1]>nums[mid]:
return nums[mid]
#如果mid大于下一个值,下一个值是变化点
if nums[mid]>nums[mid+1]:
return nums[mid+1]
#如果nums[mid]>nums[0],那么[0,mid]都是升序的
if nums[mid]>=nums[0]:
#更新左边界
left=mid+1
else:
#更新右边界
right=mid-1
第十章 字典树
1、Leetcode 208:实现前缀树
解题思路
相对而言比较简单,结构为集合套集合。具体步骤解释在代码中。
代码实现
class Trie:
def __init__(self):
"""
Initialize your data structure here.
"""
#定义一个tree,以字典的形式
self.look_up={}
def insert(self, word: str) -> None:
"""
Inserts a word into the trie.
"""
tree=self.look_up
#遍历单词中出现的字母
for char in word:
#如果当前层没有该字母
if char not in tree:
#建立当前层字母的子树
tree[char]={}
#位置移动到下一层
tree=tree[char]
#在最后加上停止符号
tree["#"]="#"
def search(self, word: str) -> bool:
"""
Returns if the word is in the trie.
"""
tree=self.look_up
#遍历单词中的字母
for char in word:
#如果当前字母不在树中:
if char not in tree:
return False
#如果在,下移一层
tree=tree[char]
#遍历结束后,必须有"#"才可以
return True if "#" in tree else False
def startsWith(self, prefix: str) -> bool:
"""
Returns if there is any word in the trie that starts with the given prefix.
"""
#与search唯一的区别是不需要考虑有没有"#"
tree=self.look_up
for char in prefix:
if char not in tree:
return False
tree=tree[char]
#如果遍历完preflix没有返回False,返回True
return True
2、Leetcode 212:单词搜索
解题思路
- 前缀树储存单词信息
- 递归的方式遍历整个棋盘。
代码实现
class Solution:
def findWords(self, board: List[List[str]], words: List[str]) -> List[str]:
#step 1:建立前缀树
root={}
#遍历所有词
for word in words:
p=root
#遍历所有字母:
for char in word:
if char not in p:
p[char]={}
#往下移动一层
p=p[char]
#标记每个单词
p["finish"]=word
#step 2:建立递归函数
m=len(board)
n=len(board[0])
res=[]
def dfs(start,p):
#定位到坐标
i,j=start[0],start[1]
#定位到坐标值
c=board[i][j]
#查看该字母在不在树中,同时查看它到达这个位置后是否有finish
#且将已经查看过的词的节点直接删除掉。
last=p[c].pop("finish",False)
#如果有finish
if last:
#将词添加
res.append(last)
#开始移动该点
board[i][j]="#"
#s四个方向
for x,y in [(1,0),(0,1),(-1,0),(0,-1)]:
new_i=i+x
new_j=j+y
#判断是否符合要求
if 0<=new_i<m and 0<=new_j<n and board[new_i][new_j] in p[c]:
#进入下一层递归
dfs((new_i,new_j),p[c])
#结束递归后,把值变回来
board[i][j]=c
if not p[c]:
p.pop(c)
#开始遍历board
for i in range(m):
for j in range(n):
if board[i][j] in root:
dfs((i,j),root)
return res
第十一章 并查集
适用场景:
组团和配对
基本操作
1、Leetcode 200: 岛屿数量
解题思路
- 建立并查集
- 遍历grid,对于每个位置为1得查看他上下左右的值,如果也为1,那么通过并查集联合他们到一起
- 问题:self.rank是做啥的。。发现把它删掉以后并不影响,所以删掉吧哈哈。
代码实现
#并查集
class UnionFind:
def __init__(self,grid):
#统计grid得长宽
m,n=len(grid),len(grid[0])
#计数变量
self.count=0
#并查集
self.parent=[-1]*(m*n)
self.rank=[0]*(m*n)
#对于grid得每个点都建立一个初始集合,统计grid中值为1的数量
for i in range(m):
for j in range(n):
if grid[i][j]=="1":
self.parent[i*n+j]=i*n+j
self.count+=1
def find(self,i):
#根的话会指向自己
if self.parent[i]!=i:
#通过递归不断去查找
self.parent[i]=self.find(self.parent[i])
return self.parent[i]
#合并的函数
def union(self,x,y):
#找到x和y的根
root_x=self.find(x)
root_y=self.find(y)
if root_x!=root_y:
if self.rank[root_x]<self.rank[root_y]:
root_x,root_y=root_y,root_x
self.parent[root_y]=root_x
if self.rank[root_y]==self.rank[root_x]:
self.rank[root_x]+=1
self.count-=1
def getCount(self):
return self.count
class Solution:
def numIslands(self, grid: List[List[str]]) -> int:
#行
row=len(grid)
if row==0:
return 0
col=len(grid[0])
nums=0
#建立并查集
uf=UnionFind(grid)
#开始遍历
for r in range(row):
for c in range(col):
if grid[r][c]=="1":
#先把它下沉
grid[r][c]="0"
#看四个方向
for x,y in [(r-1,c),(r+1,c),(r,c-1),(r,c+1)]:
if 0<=x<row and 0<=y<col and grid[x][y]=="1":
#将x,y对应的坐标点和转移前的点合并做合并
uf.union(r*col+c,x*col+y)
return uf.getCount()
2、Leetcode 130:被围绕的区域
解题思路
- 建立并查集
- 把所有在边缘的O算成一类total
- 遍历其他的,如果不在边缘看他上下左右是不是O,把连接的O算作一类
- 遍历一遍,看每个位置和total是不是一类,是的话留些O,不是变成X
代码实现
class Solution:
def solve(self, board: List[List[str]]) -> None:
"""
Do not return anything, modify board in-place instead.
"""
f={}
def find(x):
f.setdefault(x,x)
if f[x]!=x:
#递归的查找并查集
f[x]=find(f[x])
return f[x]
def union(x,y):
#将y指向x
f[find(y)]=find(x)
if not board or not board[0]:
return
row=len(board)
col=len(board[0])
total=row*col
for i in range(row):
for j in range(col):
#如果当前为O
if board[i][j]=="O":
#如果是在边缘的O
if i==0 or i==row-1 or j==0 or j==col-1:
union(i*col+j,total)
else:
for x,y in[(i+1,j),(i-1,j),(i,j+1),(i,j-1)]:
if 0<=x<row and 0<=y<col and board[x][y]=="O":
#如果是相连的O,合并
union(x*col+y,i*col+j)
for i in range(row):
for j in range(col):
if find(total)==find(i*col+j):
board[i][j]="O"
else:
board[i][j]="X"
附上一段dfs的代码
class Solution:
def solve(self, board: List[List[str]]) -> None:
"""
Do not return anything, modify board in-place instead.
"""
#先判断特殊条件
if not board or not board[0]:
return
#建立dfs
def dfs(x,y):
#先把这个点变成a
board[x][y]="a"
#四个方向
for (r,c) in [(x+1,y),(x-1,y),(x,y-1),(x,y+1)]:
if 0<=r<len(board) and 0<=c<len(board[0]) and board[r][c]=="O":
dfs(r,c)
#先看上面一行和下面一行
for j in range(len(board[0])):
if board[0][j]=="O":
dfs(0,j)
if board[len(board)-1][j]=="O":
dfs(len(board)-1,j)
#再看左面一列和右边一列
col=len(board[0])
row=len(board)
for i in range(row):
if board[i][0]=="O":
dfs(i,0)
if board[i][col-1]=="O":
dfs(i,col-1)
#最后一次遍历
for i in range(row):
for j in range(col):
if board[i][j]=="O":
board[i][j]="X"
if board[i][j]=="a":
board[i][j]="O"
第十二章 高级搜索
1、Leetcode 22 括号生成重新
该题在重新时思路上还是比较清晰的,但第一次提交错误,因为没有在循环结束后将原始的可能pop掉。
代码实现
class Solution:
def generateParenthesis(self, n: int) -> List[str]:
#定义一个存储结果的列表
res=[]
def dfs(left,right,temp):
#终止条件
if left==n and right==n:
res.append("".join(temp))
return
#对于左括号的剪枝
if left<n:
#可以将字符串中加入一个左括号
temp.append("(")
#对当前情况继续递归
dfs(left+1,right,temp)
temp.pop()
#对于右括号的剪枝,必须小于左括号的个数才可以添加
if right<left:
temp.append(")")
dfs(left,right+1,temp)
temp.pop()
dfs(0,0,[])
return res
2、Leetcode 51 :N皇后重写
代码实现
class Solution:
def solveNQueens(self, n: int) -> List[List[str]]:
#存储结果的列表
res=[]
#存储列信息的集合
col_set=set()
#存储pie信息的
pie=set()
#存储na信息
na=set()
#建立一个递归函数
def dfs(n,row,state):
#终止条件
if row==n:
res.append(state)
#对于当前行的每一列进行处理
for col in range(n):
#要保证当前列位置不存在于那三个集合
if col+row in pie or row-col in na or col in col_set:
continue
#如果不在,首先要添加信息至三个集合
col_set.add(col)
pie.add(col+row)
na.add(row-col)
#对于该层已经放好了,那么就可以进入下一层
dfs(n,row+1,state+[col])
#返回时要把添加的信息删掉
col_set.remove(col)
pie.remove(col+row)
na.remove(row-col)
#建立一个函数生成结果
def generated_result(res):
result=[]
#res里存储的是每个皇后放置的n个列信息
for re in res:
#拿出每一个列信息
for i in re:
result.append("."*i+"Q"+"."*(n-i-1))
#再把这些元素n个n个的取出来
return [ result[i:i+n] for i in range(0,len(result),n)]
dfs(n,0,[])
return generated_result(res)
3、Leetcode 36:有效的数独
代码实现
class Solution:
def isValidSudoku(self, board: List[List[str]]) -> bool:
#建立存储行,列和box信息的list({})
row_num=[{} for i in range(9)]
col_num=[{} for _ in range(9)]
box_num=[{} for j in range(9)]
row=len(board)
col=len(board[0])
#开始遍历数独中的元素
for i in range(row):
for j in range(col):
if board[i][j]!=".":
#拿出其中的数字
num=int(board[i][j])
#把行中的数字对应的位数+1
row_num[i][num]=row_num[i].get(num,0)+1
#把列中的数字对应的位数+1
col_num[j][num]=col_num[j].get(num,0)+1
#定位到该位置所在的box
box=(i//3)*3+(j//3)
#把box中的数字对应的位数+1
box_num[box][num]=box_num[box].get(num,0)+1
#判断条件
if row_num[i][num]>1 or col_num[j][num]>1 or box_num[box][num]>1:
return False
return True
4、Leetcode 37:解数独
解题思路
核心思路中最主要的有三点
- 建立三个集合存储对于每一行、每一列、每一个box中还可以用的数字
- 要遍历一次数独,把所有的已经有信息的数字的点在三个集合中删除,同时存储那些需要填数字的点的信息
- 最后一个核心也是最为重要的,遍历需要填充的点的时候,要查看这个点的行、列、box中的可用数字的交集,相当于三条路的交集的数字才可以满足三个集合中可用的信息。这点是最为重要的
代码实现
class Solution:
def solveSudoku(self, board: List[List[str]]) -> None:
"""
Do not return anything, modify board in-place instead.
"""
#行可用数字
row_set=[set(range(1,10))for _ in range(9)]
col_set=[set(range(1,10))for _ in range(9)]
box_set=[set(range(1,10))for _ in range(9)]
#收集需要填充的位置
empty=[]
for i in range(9):
for j in range(9):
if board[i][j]!=".":
val=int(board[i][j])
row_set[i].remove(val)
col_set[j].remove(val)
box_set[(i//3)*3+j//3].remove(val)
else:
empty.append((i,j))
def dfs(iters=0):
#终止条件
if iters==len(empty):
return True
#定位当前坐标
x,y=empty[iters]
#定位当前box
box=(x//3)*3+y//3
#遍历可用的数字
for val in row_set[x]&col_set[y]&box_set[box]:
#先把这些可用的数字拿出去
row_set[x].remove(val)
col_set[y].remove(val)
box_set[box].remove(val)
#将该位置填上可选元素
board[x][y]=str(val)
#继续下一个位置的迭代
if dfs(iters+1):
return True
#回溯
row_set[x].add(val)
col_set[y].add(val)
box_set[box].add(val)
return False
dfs()
5、Leetcode 127:单词接龙重写
代码实现
class Solution:
def ladderLength(self, beginWord: str, endWord: str, wordList: List[str]) -> int:
#定义一个函数把wordlist中的词存入词典,编号
def addWord(word):
if word not in wordid:
nonlocal nodeNum
wordid[word]=nodeNum
nodeNum+=1
#定义一个函数,把word_list中所有的词生成它的少一位的变化词
def addEdge(word):
#先添加字典
addWord(word)
#获取id
id1=wordid[word]
#将该单词每个字符列表话
chars=list(word)
#遍历每个字母
for i in range(len(chars)):
#拿到每个字母
temp=chars[i]
#把该字母替换
chars[i]="*"
#生成边际词
new_char="".join(chars)
#将边际词添加到wordid编号
addWord(new_char)
#获取id
id2=wordid[new_char]
#将id1对准每一个边际词
edge[id1].append(id2)
#将id2对准它可能能生成的词
edge[id2].append(id1)
#每一次把变幻的位置复原
chars[i]=temp
wordid=dict()
edge=collections.defaultdict(list)
nodeNum=0
#把wordlist中的词,编号并生成边际词
for word in wordList:
addEdge(word)
#把起始词也加入进去
addEdge(beginWord)
#判断结束词在不在wordlist中,不在的话直接返回0
if endWord not in wordid:
return 0
#建立从beginword 出发的存储列表
disBegin=[float("inf")]*nodeNum
#获取beginword的id
begin_id=wordid[beginWord]
#初始化beginword
disBegin[begin_id]=0
#建立队列
queue1=collections.deque([begin_id])
#对结束词也做上述操作
disEnd=[float("inf")]*nodeNum
end_id=wordid[endWord]
disEnd[end_id]=0
queue2=collections.deque([end_id])
#开始对两个队列进行循环
while queue1 or queue2:
#先走beginword
m=len(queue1)
for i in range(m):
nodeBegin=queue1.popleft()
#终止条件,当前id出现在了end中
if disEnd[nodeBegin]!=float("inf"):
return (disBegin[nodeBegin]+disEnd[nodeBegin])//2+1
#当前层,遍历当前nodeend所有可能的边际词
for it in edge[nodeBegin]:
#如果是还没处理过的
if disBegin[it]==float("inf"):
#操作+1
disBegin[it]=disBegin[nodeBegin]+1
#压入队列
queue1.append(it)
for j in range(len(queue2)):
nodeEnd=queue2.popleft()
#终止条件
if disBegin[nodeEnd]!=float("inf"):
return (disBegin[nodeEnd]+disEnd[nodeEnd])//2+1
for it in edge[nodeEnd]:
if disEnd[it]==float("inf"):
disEnd[it]=disEnd[nodeEnd]+1
queue2.append(it)
return 0
6、Leetcode 433:最小基因变化重新
代码实现
这道题因为每个单词只有三个转移的状态,所以不需要上一题一样对于每个词都生成边际词。
class Solution:
def minMutation(self, start: str, end: str, bank: List[str]) -> int:
#建立一个对照字典
dic={"A":"CGT","C":"AGT","G":"ACT","T":"ACG"}
queue=[(start,0)]
while queue:
word,step=queue.pop(0)
#终止条件
if word==end:
return step
#处理当前层
for i,k in enumerate(word):
for p in dic[k]:
new_word=word[:i]+p+word[i+1:]
if new_word in bank:
bank.remove(new_word)
queue.append((new_word,step+1))
return -1
7、Leetcode 773:滑动谜题
解题思路
该题看似复杂,其实搞清楚三点即可
- key 1: 将板子的位置通过012345标记后,每次移动后的处理以字符串形式获得,那么终止条件为"012345"。
- key 2:对于一个空的位置,我们可移动的板子就是与它相邻的几个位置,比如对于位置0为空时,我们只能移动位置1或者位置3,而当我们移动了位置1时,在下一个时刻位置1变为空了,即我们用一个队列去维护递归的状态,每个时刻我们要存储当前的数字顺序和当前空的位置。
- key 3: 广度优先遍历,对于每个时刻的几种移动情况,将其压入队列。
代码实现
class Solution:
def slidingPuzzle(self, board: List[List[int]]) -> int:
moves={0:[1,3],1:[0,2,4],2:[1,5],3:[0,4],4:[1,3,5],5:[2,4]}
used=set()
#定义次数的变量
num=0
#得到当前板子的字符串形式的数字
s="".join(str(c) for row in board for c in row)
#建立队列,定位到0所在的位置
q=[(s,s.index("0"))]
#开始循环
while q:
new=[]
#拿出当前板子的数字顺序和空位置
for s,i in q:
#添加集合去重
used.add(s)
#终止条件
if s=="123450":
return num
#将数字顺序列表话
arr=[c for c in s]
#遍历当前空位置每种可能的移动的结果
for move in moves[i]:
new_arr=arr[:]
#将空位置和移动到空位置的板子的数字交换位置
new_arr[i],new_arr[move]=new_arr[move],new_arr[i]
#将当前顺序字符串化
new_s="".join(new_arr)
#判断是否重复
if new_s not in used:
#如果不重复,把移动一步的顺序和当前空位置添加入new中
new.append((new_s,move))
num+=1
#将当前所有可能移动到空位置的情况压入队列
q=new
return -1
第十三章 红黑树和AVL树
第十四章 排序算法
1、简单的排序
冒泡排序
遍历每个位置的元素,与相邻的数字作比较,不断交换位置。
def main(nums):
n=len(nums)
for i in range(n):
for j in range(0,n-i-1):
if nums[j]>nums[j+1]:
nums[j],nums[j+1]=nums[j+1],nums[j]
print(nums)
选择排序
每次遍历都找到当前最小值的下标,按照顺序依次放到列表对应位置
def main(nums):
n=len(nums)
for i in range(n):
cur_min = i
for j in range(i+1,n):
if nums[j]<nums[cur_min]:
cur_min=j
nums[i],nums[cur_min]=nums[cur_min],nums[i]
print(nums)
插入排序
def main(nums):
n=len(nums)
for i in range(1,n):
j=i
while j>0:
if nums[j]<nums[j-1]:
nums[j],nums[j-1]=nums[j-1],nums[j]
j-=1
else:
break
print(nums)
希尔排序
def main(list):
n=len(list)
gap=n//2
while gap>0:
for i in range(gap,n):
j=i
while j>=gap:
if list[j-gap]>list[j]:
list[j],list[j-gap]=list[j-gap],list[j]
j-=gap
else:
break
gap//=2
return list
2、高级排序
快速排序
def quick_sort(nums,left,right):
if left>=right:
return
mid=nums[left]
low=left
high=right
while low<high:
while nums[high]>=mid and low<high:
high-=1
nums[low]=nums[high]
while nums[low]<=mid and low < high:
low+=1
nums[high]=nums[low]
nums[low]=mid
quick_sort(nums,left,low)
quick_sort(nums,low+1,right)
归并排序
def merge_sort(list):
n=len(list)
mid=n//2
if n<=1:
return list
left_list=merge_sort(list[:mid])
right_list=merge_sort(list[mid:])
left_cur=0
right_cur=0
result=[]
while left_cur<len(left_list) and right_cur<len(right_list):
if left_list[left_cur]<right_list[right_cur]:
result.append(left_list[left_cur])
left_cur+=1
else:
result.append(right_list[right_cur])
right_cur+=1
result.extend(left_list[left_cur:])
result.extend(right_list[right_cur:])
return result
3、Leetcode 1122:数组的相对排序
解题思路
将arr1中的值和对应出现的位置存储在字典中,建立一个cmp函数如果当前x在rank中返回0,rank[i],如果不在返回(1,x),根据这个key对arr1进行排序
代码实现
class Solution:
def relativeSortArray(self, arr1: List[int], arr2: List[int]) -> List[int]:
def cmp(x):
return (0,rank[x]) if x in rank else(1,x)
rank={k:i for i,k in enumerate(arr2)}
arr1.sort(key=cmp)
return arr1
4、Leetcode 242:有效的字母异位词
之前使用的是哈希表来存储s和t,这里使用排序对列表化字符串进行排序然后再变成字符串进行比较。
代码实现
class Solution:
def isAnagram(self, s: str, t: str) -> bool:
def str2list(words):
li=list(words)
li.sort()
return "".join(li)
return str2list(s)==str2list(t)
5、Leetcode 1244:力扣排行榜
解题思路
这道题其实没什么难度,主要是返回topk的总数,这里的做法参考了题解,即把字典中的value拿出来排序存储于列表,再统计k个的组合。也可以直接对字典进行排序然后遍历k次。感觉应该都差不多。如果用heap直接压堆可能会更快一点。
代码实现
class Leaderboard:
def __init__(self):
#建立一个字典
self.dic=collections.defaultdict(int)
def addScore(self, playerId: int, score: int) -> None:
self.dic[playerId]+=score
def top(self, K: int) -> int:
#先要根据value进行排序
dic1=sorted([v for v in self.dic.values()],reverse=True)
return sum(dic1[:K])
def reset(self, playerId: int) -> None:
self.dic[playerId]=0
6、Leetcode 56:合并区间
解题思路
首先将区间根据区间起始位置进行排序,然后遍历每个区间,维护一个列表,如果当前列表没有或者当前区间的起始位置大于列表中最后一个区间的终止位置,那么就无需合并,直接添加。如果当前区间的起始位置小于了上个区间的终止位置,需要合并。将列表最后一个区间的终止位置改成当前区间的终止位置。
代码实现
class Solution:
def merge(self, intervals: List[List[int]]) -> List[List[int]]:
#先根据起始位置进行排序
intervals.sort(key=lambda x:x[0])
res=[]
#遍历每个区间
for interval in intervals:
#如果当前已经加入res的区间的结束位置小于当前interval的起始位置,直接添加即可
if not res or res[-1][-1]<interval[0]:
res.append(interval)
#如果当前interval的起始值小于merge中存储interval的终止位置,那要将它们合并
else:
res[-1][-1]=max(res[-1][-1],interval[1])
return res
7、剑指Offer 51 数组中的逆序对
题目描述
代码实现
class Solution:
def reversePairs(self, nums: List[int]) -> int:
tmp=[0]*len(nums)
#归并排序
def merge_sort(l,r):
#终止条件:
if l>=r:
return 0
#递归的mid
mid=(l+r)//2
#左右分别递归
res=merge_sort(l,mid)+merge_sort(mid+1,r)
#合并阶段
#定义两个指针
i,j=l,mid+1
#找到当前列表的值域
tmp[l:r+1]=nums[l:r+1]
#遍历tmp
for k in range(l,r+1):
#如果左指针已经走完,那就不算添加右边的值
if i==mid+1:
nums[k]=tmp[j]
j+=1
#如果右指针已经走完或者当前左指针的值小于右指针
elif j==r+1 or tmp[i]<=tmp[j]:
nums[k]=tmp[i]
i+=1
#如果当前左指针大于右指针,那在添加右指针的同时还要统计逆序对的数量
else:
nums[k]=tmp[j]
j+=1
#逆序对的数量为左边列表个数减去当前位置i
res+=mid-i+1
return res
return merge_sort(0,len(nums)-1)
8、Leetcode 491: 翻转对
解题思路
这道题讲道理花费了很长时间,想从上一题直接添加一个判断是否两倍的条件来输出,发现不是很对,因为对于2,3;1这两个子序列,如果在比较2和1不满足两倍以上这个条件后,1就会被加入列表,j的下标也会移动就无法判断3,1了。想了半天发现还是在比较外再添加两个元素,再遍历一遍去添加。
代码实现
class Solution:
def reversePairs(self, nums: List[int]) -> int:
tmp=[0]*len(nums)
#归并排序
def merge_sort(l,r):
#终止条件
if l>=r:
return 0
#求出mid的位置
mid=(l+r)//2
res=merge_sort(l,mid)+merge_sort(mid+1,r)
#合并阶段,定义两个指针,指向两个子列表的开头
i,j=l,mid+1
#找到当前左右子列表的值域
tmp[l:r+1]=nums[l:r+1]
#开始遍历
for k in range(l,r+1):
#如果左指针走完,就把每个位置对应右指针
if i==mid+1:
nums[k]=tmp[j]
j+=1
#如果右指针走完或者当前左指针的值小于右指针的值
elif j==r+1 or tmp[i]<=tmp[j]:
nums[k]=tmp[i]
i+=1
#如果当前左指针的值大于右指针的值
else:
nums[k]=tmp[j]
j+=1
ti, tj = l, mid + 1
while ti <= mid and tj <= r:
if tmp[ti] <= 2 * tmp[tj]:
ti += 1
else:
res+= mid - ti + 1
tj += 1
return res
return merge_sort(0,len(nums)-1)
第十五章 字符串相关问题
1、Leetcode 709 转换成小写字母
这道题超级简单,就不做描述了
class Solution:
def toLowerCase(self, str: str) -> str:
#建立一个空字符串
word=""
#遍历str
for char in str:
word+=char.lower()
return word
2、Leetcode 58:最后一个单词的长度
第一遍提交报错是因为没有考虑多个空格的情况。所以通过判断切割后的字列表的长度判断是否全为空格。
class Solution:
def lengthOfLastWord(self, s: str) -> int:
#将字符串分隔开
word_list=s.split()
#如果为空
if len(word_list)==0:
return 0
return len(word_list[-1])
3、Leetcode 771:宝石与石头
代码实现
class Solution:
def numJewelsInStones(self, jewels: str, stones: str) -> int:
#将宝石类型列表化
list_j=list(jewels)
#统计变量
count=0
#遍历stones
for stone in stones:
if stone in list_j:
count+=1
return count
4、剑指offer 50:第一个只出现一次的字符
代码实现
class Solution:
def firstUniqChar(self, s: str) -> str:
if len(s)==0:
return " "
#先统计s的每个词出现的次数
dic=collections.defaultdict(list)
i=0
for char in s:
#把每个字母出现在s的位置作为value
dic[char].append(i)
i+=1
#遍历哈希表
for k,v in dic.items():
#第一次出现字母对应的位置只有一个的时候,返回其值
if len(v)==1:
return k
#如果遍历完都没出现
return " "
5、Leetcode 8:字符串转换整数
解题思路
使用re.findall(str)匹配正则,正则表达式:字符串形式,以正负号开头的数字(d)
上下界都要有规定。
代码实现
import re
class Solution:
def myAtoi(self, str: str) -> int:
INT_MAX = 2**31-1
INT_MIN = -2**31
str = str.lstrip() #清除左边多余的空格
num_re = re.compile(r'^[\+\-]?\d+') #设置正则规则
num = num_re.findall(str) #查找匹配的内容
num = int(*num) #由于返回的是个列表,解包并且转换成整数
return max(min(num,INT_MAX),INT_MIN) #返回值
不使用正则的方法:
class Solution:
def myAtoi(self, s: str) -> int:
#判断是否为空
#去除空格
slices=list(s.strip())
if len(slices)==0:return 0
#对于正负号的处理
signal= -1 if slices[0]=="-" else 1
#删除正负号
if slices[0] in ["+","-"]: del slices[0]
res,i=0,0
#遍历字符串且只考虑是数字的字符
while i <len(slices) and slices[i].isdigit():
res=res*10+ord(slices[i])-ord("0")
i+=1
#返回
return max(-2**31,min(signal*res,2**31-1))
6、Leetcode 14:最长公共前缀
分治代码
class Solution:
def longestCommonPrefix(self, strs: List[str]) -> str:
#分治的方法
def dfs(start,end):
#终止条件
if start==end:return strs[start]
#开始递归
mid=(start+end)//2
left=dfs(start,mid)
right=dfs(mid+1,end)
#对比两个词的长度取最小
min_len=min(len(left),len(right))
#遍历这个最小长度
for i in range(min_len):
if left[i]!=right[i]:
return left[:i]
#如果一直相同,就返回最短的词
return left[:min_len]
return "" if len(strs)==0 else dfs(0,len(strs)-1)
纵向比较代码
class Solution:
def longestCommonPrefix(self, strs: List[str]) -> str:
#特殊情况
if not strs:
return ""
#拿出一个字作为标准,因为是公共前缀,所以哪个都可以
length=len(strs[0])
#统计有多少个词
count=len(strs)
#遍历标准词的每一个位置
for i in range(length):
#如果i到达了其他词的最大长度或者当前标准词的位置和其他词的相同位置不同,结束
if any(i==len(strs[j]) or strs[j][i]!=strs[0][i] for j in range(1,count)):
return strs[0][:i]
#如果完全相同
return strs[0]
7、Leetcode 344:反转字符串
代码实现
这种题是真实存在的么,。。。。。
class Solution:
def reverseString(self, s: List[str]) -> None:
"""
Do not return anything, modify s in-place instead.
"""
return s.reverse()
8、Leetcode 541:反转字符串ii
解题思路
其实这道题作为简单题唯一的一点小的难点在于不足2k个的时候怎么处理,在下面的代码中可以看到,我们是隔2k个一取得,当最后不足k个的时候依然进行了反转,当在k和2k之间时,大于k得就没有反转,满足题意。
代码实现
class Solution:
def reverseStr(self, s: str, k: int) -> str:
n=len(s)
li=list(s)
for i in range(0,n,k*2):
#将前k个进行交换
li[i:i+k]=s[i:i+k][::-1]
return "".join(li)
9、Leetcode 151:反转字符串里的单词
解题思路
- 切片
- 反转
- 列表变字符串
代码实现
class Solution:
def reverseWords(self, s: str) -> str:
#先将单词取出储存于列表
word_list=s.split()
#将列表反转
word_list.reverse()
#输出
return " ".join(word_list)
10、Leetcode 557:反转字符串中的单词III
解题思路
没看题解,不知道还有没有更好的方法。步骤:
- 每个单词空格切分,对每个单词列表化:list of list
- 对于每个list后的词,翻转,转换为字符串添加到res
- res转换为字符串,空格分开。
代码实现
class Solution:
def reverseWords(self, s: str) -> str:
res=[]
#切片
word_list=[list(word) for word in s.split()]
for word in word_list:
word.reverse()
res.append("".join(word))
return " ".join(res)
11、Leetcode 917:仅仅反转字母
解题思路
感觉自己的代码写的真的很繁琐。。。。
- 1、把S中纯字母的部分拿出来,列表化为char_list,翻转
- 2、遍历列表化的S,对于为字母的位置,添加char_list得元素,对于为符号的,移动i指针
- 3、join返回
代码实现
class Solution:
def reverseOnlyLetters(self, S: str) -> str:
#先把S中的纯字母倒叙拿出
char_list=[char for char in S if char.isalpha()]
#翻转一下
char_list.reverse()
#遍历S,把char为纯字母的地方插入char_list
i,j=0,0
pre_list=list(S)
while i < len(S):
if S[i].isalpha():
pre_list[i]=char_list[j]
i+=1
j+=1
else:
i+=1
return "".join(pre_list)
参考了题解,直接用栈取存储需要反转的字母,这样不需要要反转只要每次pop就可以,真的妙极了!!!!!!!!!
class Solution(object):
def reverseOnlyLetters(self, S):
letters = [c for c in S if c.isalpha()]
ans = []
for c in S:
if c.isalpha():
ans.append(letters.pop())
else:
ans.append(c)
return "".join(ans)
12、Leetcode 242:有效的字母异位词重写
解题思路
- 排序
- 哈希表
代码实现
class Solution:
def isAnagram(self, s: str, t: str) -> bool:
#排序
li1=list(s)
li2=list(t)
li1.sort()
li2.sort()
return li1==li2
13、Leetcode 49:字母异位词分组:
写过好多次了,不解释了,哈希表用起来,返回list of list
class Solution:
def groupAnagrams(self, strs: List[str]) -> List[List[str]]:
#建立字典
dic=collections.defaultdict(list)
#遍历单词
for word in strs:
key="".join(sorted(word))
dic[key].append(word)
return [ v for k,v in dic.items()]
14、Leetcode 438:找到字符串中的所有字母异位词
解题思路
规定两个个p和s得长度为26得列表存储它们对应的词,第一次先查看s得前m个字符(m为p的长度),判断一下他们是否相同,然后在遍历s的过程中不算的对s_cnt进行加减,新位置的字母对应的位置相加,原来位置的字母在s_cnt得位置减掉,当s_cnt和p_cnt相等时,代表当前为字母异位词,添加当前位置的第一个索引i-(m-1)到res中。
代码实现
class Solution:
def findAnagrams(self, s: str, p: str) -> List[int]:
n, m, res = len(s), len(p), []
if n < m: return res
p_cnt = [0] * 26
s_cnt = [0] * 26
for i in range(m):
p_cnt[ord(p[i]) - ord('a')] += 1
s_cnt[ord(s[i]) - ord('a')] += 1
if s_cnt == p_cnt:
res.append(0)
for i in range(m, n):
s_cnt[ord(s[i - m]) - ord('a')] -= 1
s_cnt[ord(s[i]) - ord('a')] += 1
if s_cnt == p_cnt:
res.append(i - m + 1)
return res
15、Leetcode 1143:最长公共子序列重写
代码实现
class Solution:
def longestCommonSubsequence(self, text1: str, text2: str) -> int:
#特殊条件:text1或者text2有一个不存在
if not text1 or not text2:
return 0
m,n=len(text1),len(text2)
#建立dp
dp=[[0]*(n+1) for _ in range(m+1)]
#开始遍历
for i in range(1,m+1):
for j in range(1,n+1):
#如果当前字符相同
if text1[i-1]==text2[j-1]:
dp[i][j]=1+dp[i-1][j-1]
#如果不同,对比i,j-1和i-1,j得更大的
else:
dp[i][j]=max(dp[i-1][j],dp[i][j-1])
return dp[-1][-1]
16、Leetcode 125:验证回文串
解题思路
也可以直接把第二步变成压栈的形式然后pop
代码实现
class Solution:
def isPalindrome(self, s: str) -> bool:
n=len(s)
#先把数字和字母添加到列表中
word_list=[c.lower() for c in s if c.isdigit() or c.isalpha()]
#定义双指针起始位置
i,j=0,len(word_list)-1
while i < j:
if word_list[i]==word_list[j]:
i+=1
j-=1
else:
return False
return True
17、Leetcode 680:验证回文字符串ii
解题思路
一开始的做法是因为只删除一次,所以先返回所有的结果,再判断这些结果是否有一个是回文串,但时间复杂度太高了。下面的做法是,因为只允许删除一次,所以当左右指针移动的过程中遇到不相等的时候,删除low或者high的其中一个,然后用一层递归,去判断删除后的是不是。
代码实现
class Solution:
def validPalindrome(self, s: str) -> bool:
def valids(left,right):
while left<right:
if s[left]==s[right]:
left+=1
right-=1
else:
return False
return True
#定位左右指针
low,high=0,len(s)-1
#循环
while low<high:
if s[low]==s[high]:
#直接移动左右指针
low+=1
high-=1
else:
#删除当前low或者high
return valids(low+1,high) or valids(low,high-1)
#如果遍历完都是相同得
return True
18、Leetcode 5:最长回文子串
解题思路
中心扩展法或者动态规划均可
代码实现
class Solution:
def expandAroundCenter(self, s, left, right):
while left >= 0 and right < len(s) and s[left] == s[right]:
left -= 1
right += 1
return left + 1, right - 1
def longestPalindrome(self, s: str) -> str:
start, end = 0, 0
for i in range(len(s)):
left1, right1 = self.expandAroundCenter(s, i, i)
left2, right2 = self.expandAroundCenter(s, i, i + 1)
if right1 - left1 > end - start:
start, end = left1, right1
if right2 - left2 > end - start:
start, end = left2, right2
return s[start: end + 1]
class Solution:
def longestPalindrome(self, s: str) -> str:
n = len(s)
dp = [[False] * n for _ in range(n)]
ans = ""
# 枚举子串的长度 l+1
for l in range(n):
# 枚举子串的起始位置 i,这样可以通过 j=i+l 得到子串的结束位置
for i in range(n):
j = i + l
if j >= len(s):
break
if l == 0:
dp[i][j] = True
elif l == 1:
dp[i][j] = (s[i] == s[j])
else:
dp[i][j] = (dp[i + 1][j - 1] and s[i] == s[j])
if dp[i][j] and l + 1 > len(ans):
ans = s[i:j+1]
return ans
19、Leetcode 72:编辑距离重写
写过好多遍了,滚瓜烂熟,直接上代码
class Solution:
def minDistance(self, word1: str, word2: str) -> int:
m,n=len(word1),len(word2)
#建立dp
dp=[[0]*(n+1) for _ in range(m+1)]
#当word1为空时
for i in range(n+1):
dp[0][i]=i
#当word2为空时,
for j in range(m+1):
dp[j][0]=j
#开始遍历
for i in range(1,m+1):
for j in range(1,n+1):
#如果当前相同
if word1[i-1]==word2[j-1]:
dp[i][j]=dp[i-1][j-1]
else:
dp[i][j]=min(dp[i-1][j-1],
dp[i-1][j],
dp[i][j-1])+1
return dp[-1][-1]
20、Leetcode 10:正则表达式匹配
解题思路
对于当前不是 “ * ” 的就只匹配当前对应位置的i和j,如果是 “ * ”,就匹配i和j-2,因为j-1可以选择不匹配。如果是.就直接返回true即可,不需要对比。
代码实现
class Solution:
def isMatch(self, s: str, p: str) -> bool:
m, n = len(s), len(p)
def matches(i: int, j: int) -> bool:
if i == 0:
return False
if p[j - 1] == '.':
return True
return s[i - 1] == p[j - 1]
f = [[False] * (n + 1) for _ in range(m + 1)]
f[0][0] = True
for i in range(m + 1):
for j in range(1, n + 1):
if p[j - 1] == '*':
f[i][j] |= f[i][j - 2]
if matches(i, j - 1):
f[i][j] |= f[i - 1][j]
else:
if matches(i, j):
f[i][j] |= f[i - 1][j - 1]
return f[m][n]
21、Leetcode 44:通配符匹配
代码实现
class Solution:
def isMatch(self, s: str, p: str) -> bool:
m,n=len(s),len(p)
#建立dp,当p为空时一定是false
dp=[[False]*(n+1) for _ in range(m+1)]
dp[0][0]=True
#当s为空,p不为空时,要看p对应的*
for i in range(1,n+1):
if p[i-1]=="*":
dp[0][i]=True
else:
break
#开始循环
for i in range(1,m+1):
for j in range(1,n+1):
#当j为*号时
if p[j-1]=="*":
dp[i][j]=dp[i][j-1]|dp[i-1][j]
elif p[j-1]=="?" or s[i-1]==p[j-1]:
dp[i][j]=dp[i-1][j-1]
return dp[-1][-1]
22、Leetcode 115:不同的子序列重写
再写的时候觉得比较需要思考的是即使当si和tj想同时,可以匹配也可以不匹配,因为没准i后面的还可以匹配到j,所以是两种情况加和的关系。
代码实现
class Solution:
def numDistinct(self, s: str, t: str) -> int:
#统计两个字符串的长度
m,n=len(s),len(t)
#以t为子串,如果t比s长,不符合题意
if m<n:
return 0
#建立储存的状态矩阵
dp=[[0]*(n+1) for _ in range(m+1)]
#初始化,如果n=0,那么它可以使s的任何子串
for i in range(m+1):
dp[i][n]=1
#如果m=0,没有字串
#开始遍历
for i in range(m-1,-1,-1):
for j in range(n-1,-1,-1):
#如果当前字母匹配
if s[i]==t[j]:
#那么有可能是从s+1,j+1转移,也可能是s+1,j转移
dp[i][j]=dp[i+1][j+1]+dp[i+1][j]
else:
#如果不相等,只能考虑s+1,j
dp[i][j]=dp[i+1][j]
return dp[0][0]
23、Leetcode 387:字符串中的第一个唯一字符
题目描述
解题思路
使用哈希表,key存储字符,value存储对应下标。
代码实现
class Solution:
def firstUniqChar(self, s: str) -> int:
#建立哈希表
dic=collections.defaultdict(list)
for i in range(len(s)):
dic[s[i]].append(i)
#遍历哈希表找到第一个次数为1的
for k,v in dic.items():
if len(v)==1:
return int(v[-1])
return -1
24、Leetcode 8:字符串转换整数重写
class Solution:
def myAtoi(self, s: str) -> int:
#对字符串左边的空格进行处理
slices=list(s.strip())
#如果为空,返回0
if len(slices)==0:
return 0
#先判断正负号
signal = -1 if slices[0]=="-" else 1
#将正负号删除
if slices[0] in ["-","+"]: del slices[0]
res,i=0,0
#开始循环
while i < len(slices) and slices[i].isdigit():
res=res*10+ord(slices[i])-ord("0")
i+=1
return max(min(2**31-1,res*signal),-2**31)
25、Leetcode 541:反转字符串II重写
class Solution:
def reverseStr(self, s: str, k: int) -> str:
n=len(s)
li=list(s)
for i in range(0,n,k*2):
li[i:i+k]=li[i:i+k][::-1]
return "".join(li)
26、Leetcode 151:翻转字符串里的单词重写
class Solution:
def reverseWords(self, s: str) -> str:
#切片
word_list=s.split()
word_list.reverse()
return " ".join(word_list)
27、Leetcode 537:反转字符串中的单词iii重写
class Solution:
def reverseWords(self, s: str) -> str:
n=len(s)
#切片
word_list=[list(word) for word in s.split()]
#遍历
res=[]
for word in word_list:
word.reverse()
res.append("".join(word))
return " ".join(res)
28、Leetcode 917:仅反转字母重写
class Solution:
def reverseOnlyLetters(self, S: str) -> str:
#将输入中纯字母的压栈
stack=[char for char in S if char.isalpha()]
#开始修改原始字符串
li=list(S)
for i in range(len(li)):
if S[i].isalpha():
new_char=stack.pop()
li[i]=new_char
else:
continue
return "".join(li)
29、Leetcode 438:找到字符串中所有字母异位词重写
class Solution:
def findAnagrams(self, s: str, p: str) -> List[int]:
#长度
m,n=len(s),len(p)
res=[]
#特殊条件
if m<n:
return []
#建立一个26位列表的映射
p_save=[0]*26
s_save=[0]*26
#对于s中的前n个数字进行添加
for i in range(n):
p_save[ord(p[i])-ord("a")]+=1
s_save[ord(s[i])-ord("a")]+=1
#判断
if p_save==s_save:
res.append(0)
#开始从下标为n开始遍历
for j in range(n,m):
#新添加的
s_save[ord(s[j])-ord("a")]+=1
#去除的
s_save[ord(s[j-n])-ord("a")]-=1
#判断
if s_save==p_save:
res.append(j-(n-1))
return res
30、Leetcode 5:最长回文串重写
class Solution:
def expand_valid(self,s,left,right):
while left>=0 and right<len(s) and s[left]==s[right]:
left-=1
right+=1
return left+1,right-1
def longestPalindrome(self, s: str) -> str:
start,end=0,0
for i in range(len(s)):
l1,r1=self.expand_valid(s,i,i)
l2,r2=self.expand_valid(s,i,i+1)
#判断
if r1-l1>end-start:
start,end=l1,r1
if r2-l2>end-start:
start,end=l2,r2
return s[start:end+1]
31、Leetcode 205:同构字符串
解题思路
两个字典存储s和t每个单词出现的对应得下标位置,如果同构,他们的字典中的下标位置的存储一定相同,很简单。
代码实现
class Solution:
def isIsomorphic(self, s: str, t: str) -> bool:
n=len(s)
dic_s=collections.defaultdict(list)
dic_t=collections.defaultdict(list)
for i in range(n):
dic_s[s[i]].append(i)
dic_t[t[i]].append(i)
li1=[v for k,v in dic_s.items()]
li2=[v for k,v in dic_t.items()]
return li1==li2
32、Leetcode 680:验证回文字符串II重写
class Solution:
def valid_str(self,s,left,right):
while left<right:
if s[left]==s[right]:
left+=1
right-=1
else:
return False
return True
def validPalindrome(self, s: str) -> bool:
low,high=0,len(s)-1
while low<high:
if s[low]==s[high]:
low+=1
high-=1
else:
return self.valid_str(s,low+1,high) or self.valid_str(s,low<