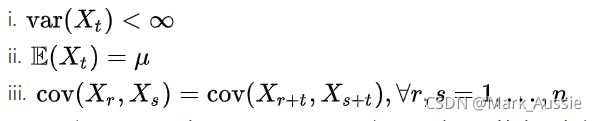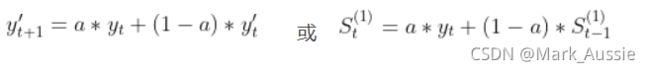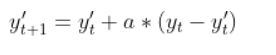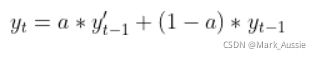时间序列平滑预测法
时间序列:统计指标的数值按照时间顺序排列的数列
时间序列分析预测法:将预测目标历史数据按时间顺序排列,按时间变化趋势外推预测目标未来值
时间序列有长期趋势、季节变动、循环变动、不规则变动。
平稳序列:Xt 为观测值集合,t 为观测时间,满足下列条件则序列(弱)平稳(弱平稳性的"弱"指在时间序列在全局上是平稳的,,即时间序列局部波动,整体上是平稳的,或随时间的变样本均值收敛)
平稳序列的期望, 方差, 协方差不随时间变化. 例如, Xt 服从同一个分布则是平稳的.
判断样本平稳性:
from statsmodels.tsa.stattools import adfuller
def test_stationarity(data, alpha=0.05, print_detail=True):
""" Test stationarity of time series data.
:param data: time series data, formatted as list
:param alpha: significance level.
:param print_detail: if True print additional information.
"""
result = adfuller(data)
is_stationary = True if result[1] <= alpha else False
if print_detail:
print('ADF statistic: %f' % result[0])
print('p-value: %f' % result[1])
print('critical values:')
for key, value in result[4].items():
print('\t%s: %.3f' % (key, value))
return is_stationary全期平均法:简单的全期平均法是对时间数列的过去数据一个不漏地全部加以同等利用;
移动平均法:移动平均法不考虑较远期数据,在加权移动平均法中给予近期资料更大的权重;
指数平滑法:指数平滑法兼容了全期平均和移动平均所长,不舍弃过去的数据,但仅给予逐渐减弱的影响程度,即随着数据的远离,赋予逐渐收敛为零的权数。
移动平均法:
T 期移动平均数:
Mt = (y(t) + y(t-1) + ... + y(t - n + 1)) / N
M(t - 1) = (y(t - 1) + y(t - 2) + ... + y(t - n)) / N
Mt = M(t - 1) + (y(t) - y(t - n)) / N --> Mt = ^y(t + 1)
移动平均法在时间序列在有明显趋势变化时会出现滞后下偏差。
可使用二次移动平均解决:
一次移动平均:Mt(1) = (yt + y(t - 1) + ... + y(t - n + 1)) / N
二次移动平均:Mt2 = (Mt(1) + Mt-1(1) + ... + Mt - n + 1(1)) / n
Mt(2) = Mt - 1(2) + (Mt(1) - Mt-n(1)) / n
指数平滑法:特殊的移动平均法,属于加权移动平均,特点是权重按照几何数级递减,越老的数据权重越小。在移动平均法基础上发展起来的一种时间序列分析预测法,通过计算指数平滑值,配合一定的时间序列预测模型对现象的未来进行预测,原理是任一期的指数平滑值都是本期实际观察值与前一期指数平滑值的加权平均。利用修匀技术,削弱短期随机波动对序列的影响,使序列平滑化,从而显示出长期趋势变化的规律。用序列过去值的加权均值来预测将来的值,序列中近期的数据被赋以较大的权重,远期的数据被赋以较小的权重。
指数平滑法可用于中短期经济发展趋势预测。
时间序列被认为由两部分组成:有规律的时间序列(即有依赖关系)+噪声(无规律,无依赖),最简单的过滤噪声的方法是:取平均。
简单滑动平均:窗口取得越长,噪声被去除的就越多,得到的信号越平稳;但信号的有用部分丢失原有特性的可能性就越大,希望发现的规律丢失的可能性就越大。
缺点:要等到至少获得T个信号才能进行平均,得到的新的信号要比原始信号短;在得到S_t的时候,只有距离 t 最近的T个原始信号。但在原始信号中,可能的信号间的相互依赖关系会跨越非常长的时间长度,如X_1可能会对X_100会产生影响,而滑动平均就会削弱甚至隐藏这种依赖关系。
指数平均 ,S_t与之前产生的所有信号有关,并且距离越近的信号所占权重越大。
一次指数平滑法:当时间数列无明显的趋势变化,可用一次指数平滑预测。
一阶指数平滑实际就是对历史数据的加权平均,可用于任何没有明显函数规律但确实存在某种前后关联的时间序列的短期预测。预测公式为:任一期的指数平滑值都是本期实际观察值与前一期指数平滑值的加权平均:下期预测值是本期预测值与以a为折扣的本期实际值与预测值误差之和。
优点:方法非常简单,甚至只要样本末期的平滑值,就可以得到预测结果;能够跟踪数据变化,预测过程中添加最新的样本数据后,新数据应取代老数据的地位,老数据会逐渐居于次要的地位,直至被淘汰。预测值总是反映最新的数据结构。
局限性:预测值不能反映趋势变动、季节波动等有规律的变动;多适用于短期预测,而不适合作中长期的预测;由于预测值是历史数据的均值,因此与实际序列的变化相比有滞后现象。
平滑系数:指数平滑预测是否理想,很大程度上取决于平滑系数。指数平滑法对实际序列具有平滑作用,平滑系数a 越小,平滑作用越强,但对实际数据的变动反应较迟缓。
两种确定指数平滑系数的方法:自动给定和人工确定。
选择自动给定,系统将按照预测误差平方和最小原则自动确定系数。如果系数接近1,说明该序列近似纯随机序列,这时最新的观测值就是最理想的预测值。
人工给定,如果序列变化比较平缓,平滑系数值应该比较小,比如小于0.1;如果序列变化比较剧烈,平滑系数值可以取得大一些,如0.3~0.5;若平滑系数值大于0.5才能跟上序列的变化,表明序列有很强的趋势,不能采用一次指数平滑进行预测。
时间序列 y1, y2, y3, ..., yt
Mt = (y(t) + y(t-1) + ... + y(t - n + 1)) / N
M(t - 1) = (y(t - 1) + y(t - 2) + ... + y(t - n)) / N
Mt = M(t - 1) + (y(t) - y(t - n)) / N
令 M(t-1) = y(t - n),Mt = yt / N + (1 - 1/N) * Mt-1
令 S(t - 1)(1) = Mt, 1/N = α --》St(1) = α * yt + (1 - α) * S(t - 1)(1)
^y(t + 1) = St(1),^y(t + 1) = α * yt + (1 - α) * ^yt
α 越大修均的作用越大,如果时间序列波动不大,α可取0.1 ~ 0.3,如波动较大可使用0.6 ~ 0.8。
上期实际值与预测值的加权平均(公式1)或下期的预测是在上期预测的基础上,根据误差做出一定的调整(公式2)。两种表述,区别只是形式上的,而实质内容是一样的。
Ft+1=αXt + (1-α) Ft (公式1)
Ft+1= Ft+ α (Xt - Ft) (公式2)
0 ≤ α ≤ 1
对移动平均法来说,移动几期平均,就得保留多少期的需求历史;
对简单指数平滑法,只需要保留两个数值:上次实际值、上次预测值。
以 [32, 35, 37, 39, 36, 37, 37, 36, 36, 39] 为时间序列上的数字,预测之后的数字,去α=0.6
使用Python 包的结果
Mydata = [32, 35, 37, 39, 36, 37, 37, 36, 36, 39] MyInput = pd.Series(Mydata, range(1, 11)) MyFirstInput = MyInput[:3].values.mean() est1 = SimpleExpSmoothing(MyInput, initialization_method='known', initial_level=MyFirstInput) r1 = est1.fit(smoothing_level=0.6, optimized=False) pred1 = r1.predict() pred2 = r1.forecast() print(pred1) # result 为37.860954
二次指数平滑:对一次指数平滑的再平滑,同时考虑历史平均和变化趋势,
适用于有线性趋势的时间数列。
二次指数平滑是直线方程,其截距为:(2yt’ - yt),斜率为:(yt’-yt) * a / (1-a),自变量为预测天数。
在一次指数平滑的基础上得二次指数平滑 的计算公式:
二次指数平滑法是对一次指数平滑值作再一次指数平滑的方法,不能单独地进行预测,必须与一次指数平滑法配合,建立预测的数学模型,运用数学模型确定预测值。
三次指数平滑:增加季节性因素。平均模型考虑的季节性效应在股票或者期货价格中都会比较常见,比如在过年前A股市场通常会交易比较频繁,在小麦成熟的时候小麦期货价格也会有比较明显的波动。但模型本身的复杂度也增加了,需要一定的经验才能比较合理地设置其中复杂的参数。
三次指数平滑预测是二次平滑基础上的再平滑,
yt+m = (3 * yt’ - 3 * yt + yt) + [(6 - 5 * a) * yt’ - (10 - 8 * a) * yt + (4 - 3 * a) * yt ] * am/2 * (1 - a)2 + (yt’ - 2yt + yt’) * a2m2/2(1 - a)2,其中, yt = a * yt-1 + (1 - a) * yt-1
参考:
时间序列平滑预测法 - 百度文库 (baidu.com)
时间序列的预测:指数平滑法 - 知乎 (zhihu.com)
使用python中SimpleExpSmoothing一阶指数平滑结果与Excel计算不同-Python-CSDN问答
时间序列预测之一:指数平滑法(一)理论_满腹的小不甘-CSDN博客_时间序列指数平滑预测法
时间序列模型简介 - 简书 (jianshu.com)