【深度学习-吴恩达】L1-4 深层神经网络
L1 深度学习概论
4 深层神经网络
课程时长共64min31s
4.1 深层神经网络
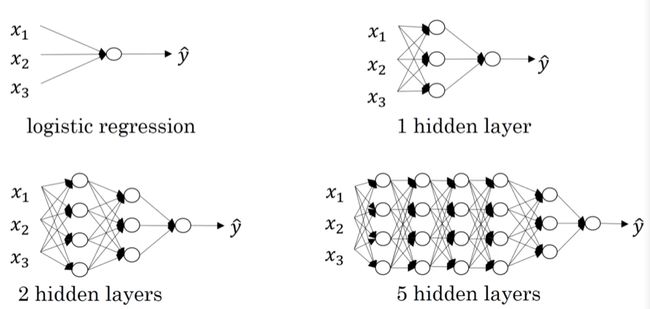
什么是深层神经网络?
对于如下一个四层神经网络
- L表示神经网络层数
- 使用n[1]表示第一层的单元数量
- n[4]=n[L]=1
- n[0]=nx=3
- a[l]第l层的激活值
- a[l]=g[l](z[l]) 第l层的激活函数
4.2 深层网络中的前向传播
对于单个输入的正向传播计算公式:
z [ l ] = W [ l ] a [ l − 1 ] + b [ l ] a [ l ] = g [ l ] ( z [ l ] ) z^{[l]}=W^{[l]}a^{[l-1]}+b^{[l]}\\ a^{[l]} = g^{[l]}(z^{[l]}) z[l]=W[l]a[l−1]+b[l]a[l]=g[l](z[l])
向量化正向传播计算公式:
Z [ l ] = W [ l ] A [ l − 1 ] + b [ l ] A [ l ] = g [ l ] ( Z [ l ] ) Z^{[l]}=W^{[l]}A^{[l-1]}+b^{[l]}\\ A^{[l]} = g^{[l]}(Z^{[l]}) Z[l]=W[l]A[l−1]+b[l]A[l]=g[l](Z[l])
- 此处需要使用for循环,没有其他更好的方法
4.3 核对矩阵的维数
对于单个输入,以下参数的维度:
z [ l ] , a [ l ] , d z [ l ] , d a [ l ] : ( n [ l ] , 1 ) W [ l ] , d W [ l ] : ( n [ l ] , n [ l − 1 ] ) b [ l ] , d b [ l ] : ( n [ l ] , 1 ) z^{[l]},a^{[l]},dz^{[l]},da^{[l]}:(n^{[l]}, 1)\\ W^{[l]}, dW^{[l]}:(n^{[l]}, n^{[l-1]})\\ b^{[l]},db^{[l]}:(n^{[l]}, 1) z[l],a[l],dz[l],da[l]:(n[l],1)W[l],dW[l]:(n[l],n[l−1])b[l],db[l]:(n[l],1)
对于m个输入,以下参数的维度:
Z [ l ] , A [ l ] , d Z [ l ] , d A [ l ] : ( n [ l ] , m ) W [ l ] , d W [ l ] : ( n [ l ] , n [ l − 1 ] ) b [ l ] , d b [ l ] : ( n [ l ] , m ) Z^{[l]},A^{[l]},dZ^{[l]},dA^{[l]}:(n^{[l]}, m)\\ W^{[l]}, dW^{[l]}:(n^{[l]}, n^{[l-1]})\\ b^{[l]},db^{[l]}:(n^{[l]}, m) Z[l],A[l],dZ[l],dA[l]:(n[l],m)W[l],dW[l]:(n[l],n[l−1])b[l],db[l]:(n[l],m)
- 在Python中Numpy使用广播机制,因此以下维度情况也可行: b [ l ] , d b [ l ] : ( n [ l ] , m ) b^{[l]},db^{[l]}:(n^{[l]}, m) b[l],db[l]:(n[l],m)
4.4 为什么使用深层表示
先学习简单特征,深层结合特征,探测更加复杂的东西
另一个,电路理论的解释
- 浅层需要使用更多门
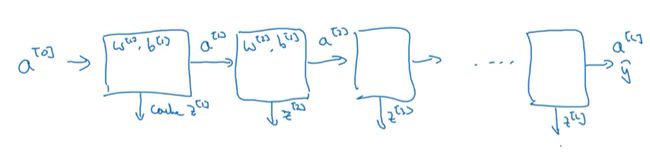
4.6 搭建深层神经网络块
正向传播过程:
- 通过输入x得到 y ^ \hat{y} y^
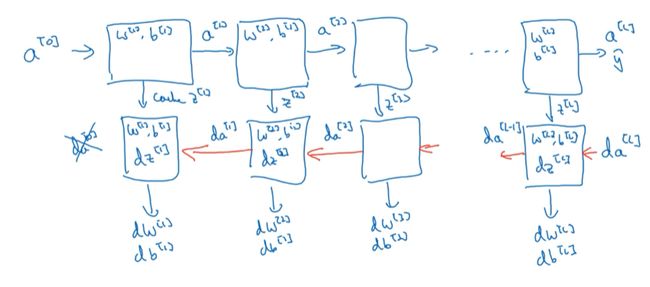
反向传播过程:
更新 W [ l ] , b [ l ] W^{[l]},b^{[l]} W[l],b[l]:
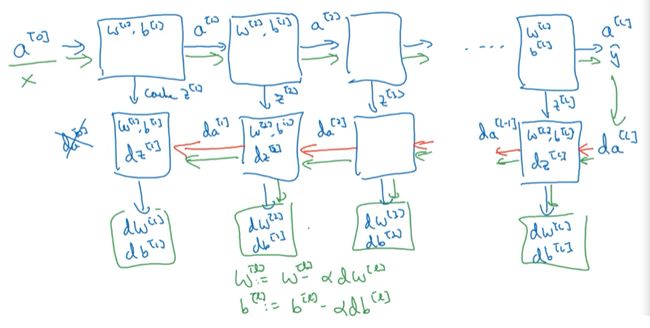
4.7 前向和反向传播
对于第 l l l层:
-
正向传播
-
输入 a [ l − 1 ] a^{[l-1]} a[l−1]
-
输出 a [ l ] , c a c h e ( z [ l ] , w [ l ] , b [ l ] ) a^{[l]},cache(z^{[l]},w^{[l]},b^{[l]}) a[l],cache(z[l],w[l],b[l])
-
首个输入数据 a [ 0 ] = x a^{[0]}=x a[0]=x
-
-
反向传播
-
输入 d a [ l ] , z [ l ] da^{[l]},z^{[l]} da[l],z[l]
-
输出 d a [ l − a ] , d W [ l ] , d b [ l ] da^{[l-a]},dW^{[l]},db^{[l]} da[l−a],dW[l],db[l]
-
首个输入数据 d a [ L ] = − y a [ L ] + 1 − y 1 − a [ L ] da^{[L]}=-\frac {y}{a^{[L]}}+\frac{1-y}{1-a^{[L]}} da[L]=−a[L]y+1−a[L]1−y
-
向量化首个输入数据 d A [ L ] = ∑ i = 1 m ( − y ( i ) a [ L ] ( i ) + 1 − y ( i ) 1 − a [ L ] ( i ) ) dA^{[L]}=\sum_{i=1}^m(-\frac {y^{(i)}}{a^{[L](i)}}+\frac{1-y^{(i)}}{1-a^{[L](i)}}) dA[L]=∑i=1m(−a[L](i)y(i)+1−a[L](i)1−y(i))
- 为什么是累加?
-
4.8 参数 VS 超参数
参数 parameter
- W [ 1 ] , W [ 2 ] , … W^{[1]},W^{[2]},\dots W[1],W[2],…
- b [ 1 ] , b [ 2 ] , … b^{[1]},b^{[2]},\dots b[1],b[2],…
超参数 hyper parameter
- 学习率α
- 梯度下降法循环数量iteration
- 隐藏层数量L
- 隐藏单元数量 n [ 1 ] , n [ 2 ] , … n^{[1]},n^{[2]},\dots n[1],n[2],…
- 激活函数的选择 g [ l ] ( z [ l ] ) g^{[l]}(z^{[l]}) g[l](z[l])
- momentum
- mini batch大小
- 不同的正则化参数