深度学习图像分类(五): ResNet
深度学习图像分类(五): ResNet
文章目录
- 深度学习图像分类(五): ResNet
- 前言
- 一、深度学习网络退化问题
- 二、残差连接
- 三、ResNet的网络结构
- 四、残差的变体
- 五、代码的实现
- 总结
前言
深度残差网络(Deep residual network, ResNet)的提出是CNN图像史上的一件里程碑事件,ResNet在2015年发表当年取得了图像分类,检测等等5项大赛第一,并又一次刷新了CNN模型在ImageNet上的历史记录。知道今天,各种最先进的模型中依然处处可见残差连接的身影,其paper引用量是cv领域第一名。ResNet的作者何恺明也因此摘得CVPR2016最佳论文奖,当然何博士的成就远不止于此,感兴趣的可以去搜一下他后来的辉煌战绩。
一、深度学习网络退化问题
从经验来看,网络的深度对模型的性能至关重要,当增加网络层数后,网络可以进行更加复杂的特征模式的提取,所以当模型更深时理论上可以取得更好的结果,从Vgg网络也可以看出网络越深而效果越好的一个实践证据。但是更深的网络其性能一定会更好吗?
实验发现深度网络出现了退化问题(Degradation problem):网络深度增加时,网络准确度出现饱和,甚至出现下降。下图节选自ResNet原论文,不管是训练阶段还是验证阶段,56层的网络比20层网络错误率还高,效果还要差。究竟是什么原因导致的这一问题?
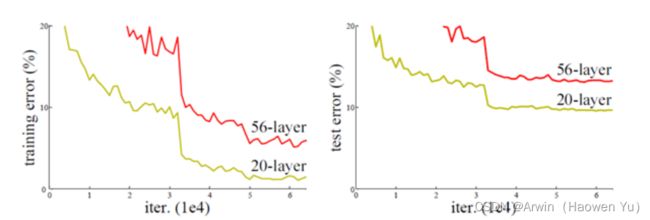
首先印入脑海的就是神经网络的常见问题:过拟合问题
但是,过拟合的一般表现为训练阶段效果很好,测试阶段效果差。这与上图明显是不相符的。
除此之外,最受人认可的原因就是梯度爆炸/弥散了。为了理解什么是梯度弥散,首先回顾一下反向传播的知识。
反向传播结果的数值大小不止取决于求导的式子,很大程度上也取决于输入的模值。当计算图每次输入的模值都大于1,那么经过很多层回传,梯度将不可避免地呈几何倍数增长,直到Nan。这就是梯度爆炸现象。当然反过来,如果我们每个阶段输入的模恒小于1,那么梯度也将不可避免地呈几何倍数下降,直到0。这就是梯度消失现象。值得一提的是,由于人为的参数设置,梯度更倾向于消失而不是爆炸。由于至今神经网络都以反向传播为参数更新的基础,所以梯度消失问题听起来很有道理。
然而,事实也并非如此,至少不止如此。我们现在无论用Pytorch还是Tensorflow,都会自然而然地加上Bacth Normalization(简称BN,在GoogLeNetV2中被提出),而BN的作用本质上也是控制每层输入的模值,因此梯度的爆炸/消失现象理应在很早就被解决了(至少解决了大半)。
不是过拟合,也不是梯度消失,这就很尴尬了……CNN没有遇到我们熟知的两个老大难问题,却还是随着模型的加深而导致效果退化。无需任何数学论证,我们都会觉得这不符合常理。
为什么说模型退化不符合常理?按理说,当我们堆叠一个模型时,理所当然的会认为效果会越堆越好。因为,假设一个比较浅的网络已经可以达到不错的效果,那么即使之后堆上去的网络什么也不做,模型的效果也不会变差。然而事实上,这却是问题所在。什么都不做”恰好是当前神经网络最难做到的东西之一。MobileNet V2的论文[2]也提到过类似的现象,由于非线性激活函数Relu的存在,每次输入到输出的过程都几乎是不可逆的(信息损失)。我们很难从输出反推回完整的输入。
也许赋予神经网络无限可能性的“非线性”让神经网络模型走得太远,使得特征随着层层前向传播得到完整保留(什么也不做)的可能性都微乎其微。用学术点的话说,这种神经网络丢失的“不忘初心”/“什么都不做”的品质叫做恒等映射(identity mapping)。因此,可以认为Residual Learning的初衷,其实是让模型的内部结构至少有恒等映射的能力。以保证在堆叠网络的过程中,网络至少不会因为继续堆叠而产生退化!
二、残差连接
刚刚讲了模型在层级结构太多的情况下退化的问题以及残差连接,那么,到底什么是残差连接?最简单的残差长下面这个样子:
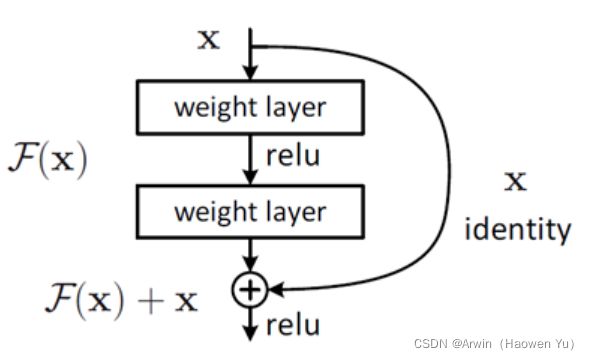
前面分析得出,如果深层网络后面的层都是是恒等映射,那么模型就可以转化为一个浅层网络。那现在的问题就是如何得到恒等映射了。事实上,已有的神经网络很难拟合潜在的恒等映射函数H(x) = x。但如果把网络设计为H(x) = F(x) + x,即直接把恒等映射作为网络的一部分。就可以把问题转化为学习一个残差函数F(x) = H(x) - x.
对于普通的神经网络,其学习到的是输入到输出的映射,即,当输入为x时, 其学习到的特征记为H(x),现在我们希望其可以学习到残差F(x) = H(x) - x ,即,当输入是x时,寻找输入x到输出H(x)减输入x的映射。这有点类似与电路中的“短路”,所以是一种短路连接。
图中右侧的曲线叫做跳接(shortcut connection),通过跳接在激活函数前,将上一层(或几层)之前的输出与本层计算的输出相加,将求和的结果输入到激活函数中做为本层的输出。
顺带一提,这里一个Block中必须至少含有两个层,否则几乎没用。
三、ResNet的网络结构
ResNet网络是参考了VGG19网络,在其基础上进行了修改,并通过短路机制加入了上图所示的残差单元。变化主要体现在ResNet直接使用stride=2的卷积做下采样(取代了VGG中的池化),并且用global average pool层替换了全连接层(这样可以接收不同尺寸的输入图像),另外模型层次明显变深。相似之处是两者都是通过堆叠3X3的卷积进行特征提取。
ResNet的一个重要设计原则是:当feature map大小降低一半时,feature map的数量增加一倍,这一定程度上减少了减少特征图尺寸时带来的信息损失。
从下图中可以看到,ResNet相比普通网络每两层间增加了短路机制,这就形成了残差学习,其中虚线表示feature map数量发生了改变。
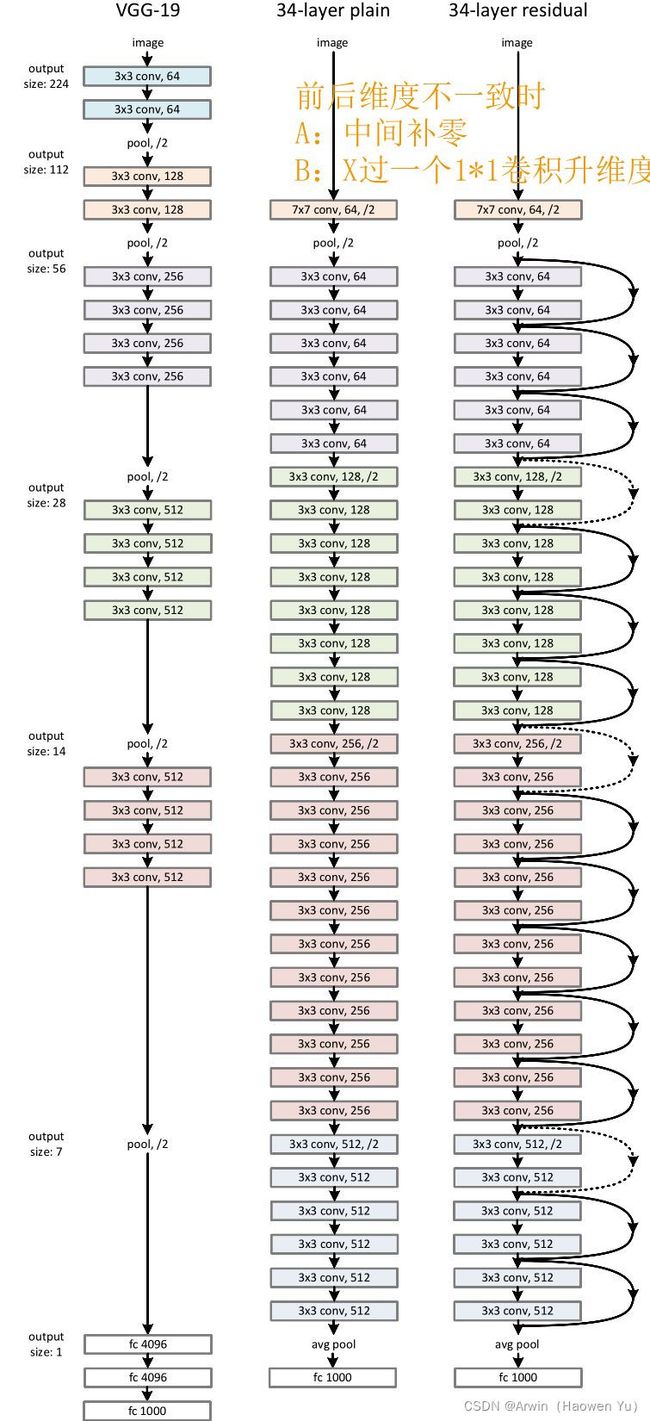
在ResNet原论文中,作者给出了五个不同层次的模型结构,分别是18层,34层,50层,101层,152层。上图所示的是34层的模型结构。下图给出所有模型的结构参数:
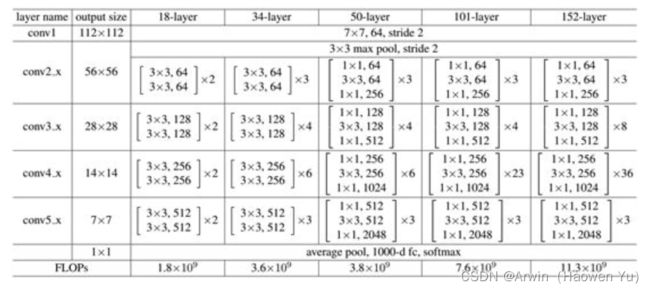
值得注意的是: 50层,101层和152层使用的残差模块与之前介绍的不同。主要原因是深层次的网络中参数量太大,为了减少参数,在3X3卷积前先通过1X1卷积对channel维度进行降维(个人感觉,其灵感来自于GoogLeNetV3中提出了网络设计准则,不了解的同学可以看我上一个博文)
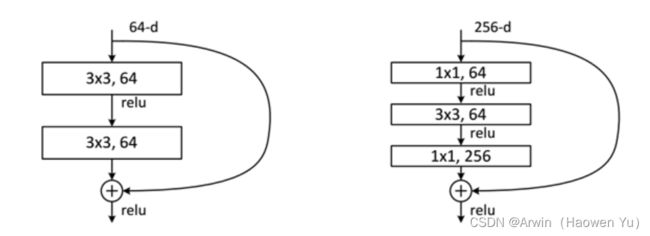
如上图所示:左图是浅层模型用的残差结构;右图是深层模型用的残差结构。
注意:对于短路连接,当输入和输出维度一致时,可以直接将输入加到输出上。但是当维度不一致时(对应的是维度增加一倍),这就不能直接相加。这时可以采用新的映射(projection shortcut),比如一般采用1x1的卷积对shortcut进行一个升维。
四、残差的变体
其实短路连接有多种调整方式,比如激活函数的位置?BN的位置?连接跨越的卷积数量?等等都是可以调整的地方。因此有文献对这些变体残差做了研究并实验。最后根据实验结果提出了一个效果最好的残差方式如下图:改进前后一个明显的变化是采用pre-activation,BN和ReLU都提前了。而且作者推荐短路连接采用恒等变换,这样保证短路连接不会有阻碍。
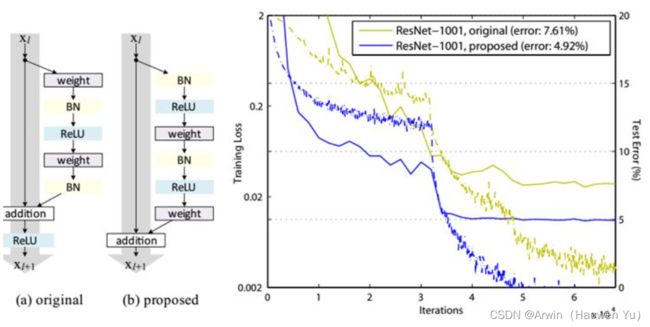
五、代码的实现
这里给出模型搭建的python代码(基于pytorch实现)。完整的代码是基于图像分类问题的(包括训练和推理脚本,自定义层等)详见我的GitHub: 完整代码连接
import torch
import torch.nn as nn
from torch.nn import functional as F
from custom_layers.CustomLayers import ConvActivation, ConvBNActivation, ConvBatchNormalization
class SmallResidual(nn.Module):
expansion = 1
def __init__(self, input_channels, output_channels, stride=1, downsample=None, **kwargs):
super().__init__()
self.conv1 = ConvBNActivation(input_channels, output_channels, kernel_size=3, stride=stride, padding=1, bias=False)
self.conv2 = ConvBatchNormalization(output_channels, output_channels, kernel_size=3, stride=1, padding=1, bias=False)
self.downsample= downsample
def forward(self, x):
indentity = x
if self.downsample is not None:
indentity = self.downsample(x)
# F.ReLU()是函数调用,一般使用在foreward函数里。而nn.ReLU()是模块调用,一般在定义网络层的时候使用。
out = self.conv1(x)
out = self.conv2(out)
out += indentity
out = F.relu(out, True)
return out
class BigResidual(nn.Module):
expansion = 4
# groups是组卷积; 用于实现ResNeXt
def __init__(self, input_channels, output_channels, stride=1, downsample=None, groups=1, width_per_group=64, **kwargs):
super().__init__()
width = int(output_channels*(width_per_group/64))*groups
self.conv1 = ConvBNActivation(input_channels=input_channels, output_channels=width, kernel_size=1, stride=1, padding=0)
self.conv2 = ConvBNActivation(input_channels=width, output_channels=width, kernel_size=3, stride=stride, padding=1, groups=groups)
self.conv3 = ConvBatchNormalization(input_channels=width, output_channels=output_channels*self.expansion, kernel_size=1, stride=1, padding=0)
self.downsample = downsample
def forward(self, x):
indentity = x
if self.downsample is not None:
indentity = self.downsample(x)
out = self.conv1(x)
out = self.conv2(out)
out = self.conv3(out)
out = out + indentity
out = F.relu(out, True)
return out
class ResNet(nn.Module):
def __init__(self, which_residual, num_blocks, num_classes=None, include_top=None, groups=1, width_per_groups=64):
super().__init__()
self.include_top = include_top
self.in_nc = 64
self.groups=groups
self.width_per_groups = width_per_groups
self.conv1 = nn.Conv2d(3, self.in_nc, kernel_size=7, stride=2, padding=3, bias=False)
self.bn1 = nn.BatchNorm2d(self.in_nc)
self.relu = nn.ReLU(True)
self.maxpool = nn.MaxPool2d(kernel_size=3, stride=2, padding=1)
self.Block1 = self._make_Block(which_residual, 64, num_blocks[0])
self.Block2 = self._make_Block(which_residual, 128, num_blocks[1], stride=2)
self.Block3 = self._make_Block(which_residual, 256, num_blocks[2], stride=2)
self.Block4 = self._make_Block(which_residual, 512, num_blocks[3], stride=2)
if self.include_top:
self.avgpool = nn.AdaptiveAvgPool2d((1,1))
self.fc = nn.Linear(512*which_residual.expansion, num_classes)
for m in self.modules():
if isinstance(m, nn.Conv2d):
nn.init.kaiming_normal_(m.weight, mode='fan_out', nonlinearity='relu')
def forward(self, x):
x = self.conv1(x)
x = self.bn1(x)
x = self.relu(x)
x = self.maxpool(x)
x = self.Block1(x)
x = self.Block2(x)
x = self.Block3(x)
x = self.Block4(x)
if self.include_top:
x = self.avgpool(x)
x = torch.flatten(x,start_dim=1)
x = self.fc(x)
return x
def _make_Block(self, which_residual, channel, num_block, stride=1):
downsample = None
if stride != 1 or self.in_nc != channel * which_residual.expansion:
downsample = nn.Sequential(
nn.Conv2d(self.in_nc, channel * which_residual.expansion, kernel_size=1, stride=stride, bias=False),
nn.BatchNorm2d(channel * which_residual.expansion))
Block = []
Block.append(which_residual(self.in_nc,
channel,
downsample=downsample,
stride=stride,
groups = self.groups,
width_per_group=self.width_per_groups))
self.in_nc = channel * which_residual.expansion
for _ in range(1, num_block):
Block.append(which_residual(self.in_nc, channel, groups=self.groups, width_per_group=self.width_per_groups))
return nn.Sequential(*Block)
def resnet34(num_classes=1000, include_top=True):
# https://download.pytorch.org/models/resnet34-333f7ec4.pth
return ResNet(SmallResidual, [3, 4, 6, 3], num_classes=num_classes, include_top=include_top)
def resnet50(num_classes=1000, include_top=True):
# https://download.pytorch.org/models/resnet50-19c8e357.pth
return ResNet(BigResidual, [3, 4, 6, 3], num_classes=num_classes, include_top=include_top)
def resnet101(num_classes=1000, include_top=True):
# https://download.pytorch.org/models/resnet101-5d3b4d8f.pth
return ResNet(BigResidual, [3, 4, 23, 3], num_classes=num_classes, include_top=include_top)
def resnext50_32x4d(num_classes=1000, include_top=True):
# https://download.pytorch.org/models/resnext50_32x4d-7cdf4587.pth
groups = 32
width_per_group = 4
return ResNet(BigResidual, [3, 4, 6, 3],
num_classes=num_classes,
include_top=include_top,
groups=groups,
width_per_group=width_per_group)
def resnext101_32x8d(num_classes=1000, include_top=True):
# https://download.pytorch.org/models/resnext101_32x8d-8ba56ff5.pth
groups = 32
width_per_group = 8
return ResNet(BigResidual, [3, 4, 23, 3],
num_classes=num_classes,
include_top=include_top,
groups=groups,
width_per_group=width_per_group)
总结
就一句话:残差真的太牛*了! 大家在阅读之后的paper会发现,之后的经典网络结构中都有残差的身影。像这种思想"简单",实现容易,效果拔群的模型创新才是学术界甚至工业界的学者们共同追求的目标,最后再次赞美一下何凯明大神:牛!