SWUST OJ#541 排列的字典序问题
目录
题目
思路
引入
本题思路
解决第一小问:求解字典序值
解决第二小问:求解字典序下一个排列
代码
题目
题目描述
n个元素{1,2,..., n }有n!个不同的排列。将这n!个排列按字典序排列,并编号为0,1,…,n!-1。每个排列的编号为其字典序值。例如,当n=3时,6 个不同排列的字典序值如下:
0 1 2 3 4 5
123 132 213 231 312 321
任务:给定n 以及n 个元素{1,2,..., n }的一个排列,计算出这个排列的字典序值,以及按字典序排列的下一个排列。
输入
第1 行是元素个数n(n < 15)。接下来的1 行是n个元素{1,2,..., n }的一个排列。
输出
第一行是字典序值,第2行是按字典序排列的下一个排列。
样例输入
8 2 6 4 5 8 1 7 3样例输出
8227 2 6 4 5 8 3 1 7
思路
引入
先来一个例子引入:这里有几个数,要求我们找出有多少个逆序对(前者大于后者)。
5 3 7 4 9 6
不难发现,逆序对有:2+0+2+0+1+0=5个
现在我们把所有数都减去2
3 1 5 2 7 4
可以发现逆序对数还是和刚才一样。
那是因为两个数,虽然值变小了,但是相对大小却是没变的。同理,如果我们让倒数第二个数"7" 再减去1。
3 1 5 2 6 4
同样的,在这种情况下逆序对数还是5,因为相对大小还是没有发生变化。
所以,我们就把这样的算法称为向内离散化,当然还有以扩大的方式:向外离散化。
离散化例题:洛谷P1496 火烧赤壁
本题思路
解决第一小问:求解字典序值
解决本题的思路就是采用离散化算法,我们不关注具体大小,只关注相对关系。
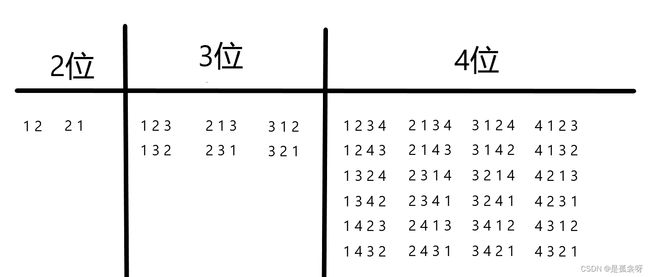
题目有8位数,然而8227也不是一眼就能推出来的,我们还是从2位,3位,4位层层往后推理。
先对每一位的数,以首数字为基准进行分类。
按照上图的分类,如果说我们知道第一个数是多少,那么我们很容易知道它是哪一个梯度的。
例如:3 4 1 2
我们很容易知道3 4 1 2是第三梯度,也就是说在第12~18之间(注意,区间都是前开后闭)
那么接下来第一个3就不用再看了,因为我们已经知道,它是属于第三梯度。
剩下的就是 4 1 2 。然后现在我们离散化处理一下,4 1 2实际上等价于3 1 2
在三位数中,我们很容易发现,它是处于第三梯度的,也就是4~6之间,和之前的相加起来,因此 3 4 1 2就存在于16~18之间。
再把第二个数抛掉,剩下的是1 2。很显然是第一梯度,所以定位:2*6+2*2+1*1 也就是第17位。
同理,再举一个例子:2 3 4 1
第一步:首数字为2,那么属于第二梯度,也就是6~12之间。
第二步:离散化后三个数为:2 3 1。首数字为2,那么属于第二梯度 也就是2~4之间。加起来也就是8~10之间。
第三步:离散化剩下两个为:2 1。首数字为2,那么也还是属于第二梯度。所以可得知为第10位。
那么题目中8位数的例子:2 6 4 5 8 1 7 3
首先第一步:首数字为2,那么属于第二梯度,也就是5040~10080之间(8位数,那么就是7的阶乘:1*7!~ 2*7!)
第二步:离散化处理剩下的为:5 3 4 7 1 6 2 。首数字为5,那么属于第五梯度,所以就是2880~3600之间(7位数,那么就说6的阶乘:4*6!~ 5*6!)加起来就是7920~8640之间。
第三步同理,处理剩下的为:3 4 6 1 5 2。首数字为3,那么属于第三梯度,所以就是240~360之间(6位数,那么就是5的阶乘:2*5!~ 3*5!)加起来就是8160~8280之间。
第四步还是一样,处理剩下的为:3 5 1 4 2。首数字为3,那么属于第三梯度,所以就是48~72之间(5位数,那么就是4的阶乘:2*4!~ 3*4!)加起来就是8208~8232之间。
第五步还是一样,处理剩下的为: 4 1 3 2。首数字为4,那么属于第四梯度,所以就是18~24之间(4位数,那么就是3的阶乘:3*3!~ 4*3!)加起来就是8226~8232之间。
第六步还是一样,处理剩下的为:1 3 2。首数字为1,那么属于第一梯度,所以就是0~2之间(3位数,那么就是2的阶乘:0*2!~ 1*2!)加起来就是8226~8228之间。
最后一步:最后两位离散化为:2 1,首数字为2,那么属于第二梯度,所以可以定位该数为第8228位。
这里注意一下,题目是从0开始的,所以要减去1,也就是第8227,那么第一问就解决了
综上所述
这问的核心思想就是离散化数组,找出首数字,一步步的缩小范围,最后定位得出。
那么代码思路(伪)就是:
ll sum=0;
for(int i=1;i<=n;i++) {
sum+=a[i]* ((n-i)!)
} //a[i]代表离散化首数字,!代表阶乘阶乘我们可以新建一个数组b,前缀积预处理一下,不至于每次都调用函数。
int b[20]={1,1};
for(int i=2;i<=20;i++) b[i]=b[i-1]*i;那么现在的问题就是离散化首数了,如果说,每次都现用现离散的话,大致估一下复杂度则会是O(n²),因为要循环判断,合起来计算最初的循环,那么就是O(n³),这样时间复杂度太高了。
所以,我们为啥不先预处理,先就离散了,再来进行计算,求是第几个数。
我们把刚刚每次离散化下来的首数整理一下为:2 5 3 3 4 1 2 1
再对比下原数组 :2 6 4 5 8 1 7 3
可以发现离散化的数组实际上就是:该数减去 前面 比他小的数的个数。例如:第5个数"8",前面4个都比他小,所以离散化下来就是4
这么一来,离散预处理就可以降低到O(n²)的复杂度了:
for(int i=1;i<=n;i++) {
for(int j=1;ja[j]) a[i]--;
}
} 解决第二小问:求解字典序下一个排列
根据之前离散化的逻辑,我们每次根据首数字找梯度,并对下一组离散化,那么无论如何,最后一个数都是可以离散化成1的,也就是说,最后一个数永远都是第一梯度。
那万一是2呢?是第二梯度呢?
那就定位结果加2呗。
由此可见我们在最后一个离散化数加上1,也就自然而然的变成了下一个数了。
a[n]++;这时候离散化数组变成:2 5 3 3 4 1 2 2
很显然,这是一个"虚假"的离散化数组。
我们还是以4位数举例:
易求得 3 1 4 2的离散化数组为:3 1 2 1
而3 1 4 2下一位是 3 2 1 4
易求得 3 2 1 4 的离散化数组为:3 2 1 1
可是,按照上述逻辑3 1 2 1的下一位离散数组也可以是3 1 2 2
之前离散化数组的求法是看前面比他小的数有多少个,那么由此可以得知在4位数的情况下,离散化每个位置最大的数为4 3 2 1依次递减。
同理,n位数每个位置最大则为:n n-1 n-2 ... ... 3 2 1
很显然这个"虚假"的数组 3 1 2 2 违背了这个规定。
所以,我们要对这个"虚假"的离散化数组进行还原。
还原方式很简单,就像上述规则一样,超过了就前一位加一,该位回归最初。
因此我们是可以推出:3 1 2 2 等价于 3 1 3 1 等价于 3 2 1 1
for(int i=n;i>=1;i--) {
if(a[i]>n-i+1) {
a[i-1]++;
a[i]=1;
}
}最后再将还原的离散化数组,再次还原为排列的数组。
根据之前离散化预处理代码,逆向操作就行了,看前面有多少数比他大,然后加回来。
for(int i=n;i>=2;i--) {
for(int j=i-1;j>=1;j--) {
if(a[i]>=a[j]) a[i]++;
}
}代码
根据上述思路,即可写出完整代码。
#include
#include
#include
#include
#define endl '\n'
#define N 5000005
typedef long long ll;
using namespace std;
ll a[20],b[20];
int main() {
ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
int n;cin>>n;
for(int i=1;i<=n;i++) cin>>a[i];
//第一问
//离散化首数
for(int i=2;i<=n;i++) {
for(int j=1;ja[j]) a[i]--;
}
}
//预处理阶乘
b[0]=b[1]=1;
for(int i=2;i<=20;i++) b[i]=b[i-1]*i;
//计算
ll sum=0; //防位数过多爆范围,虽然题目最大15,15倒不会爆
for(int i=1;i<=n;i++) {
sum+=(a[i]-1)*b[n-i];
}
cout<=2;i--) {
if(a[i]>n-i+1) {
a[i-1]++;
a[i]=1;
}
}
//还原离散化
for(int i=n;i>=2;i--) {
for(int j=i-1;j>=1;j--) {
if(a[i]>=a[j]) a[i]++;
}
}
for(int i=1;i<=n;i++) cout<