01.朴素贝叶斯介绍

【数学基础】

1. 概率

• 条件概率：
  事件A在事件B发生的前提下发生的概率，表示为：P(A|B)，读作A在B发生的条件下发生的概率。
• 联合概率：
  两个事件共同发生的概率，比如事件A和B的联合概率表示为：P(AB)或者P(A,B)。
• 边缘概率：
  是对某个事件发生的概率，而与其他事件无关，比如事件A的边缘概率表示为P(A)，同样事件B的边缘概率表示为P(B)。
• 条件概率的链式法则：
  P(A,B) = P(A) * P(B|A)
  如果A事件和B事件是互相独立，那么P(B|A)=P(B)，其对应联合概率：
  P(A,B) = P(A) * P(B)

2. 贝叶斯公式

P(A|B) = P(B|A) * P(A) / P(B)
推导：
=> P(A,B) = P(A) * P(B|A)
=> P(B,A) = P(B) * P(A|B)
=> P(A,B) = P(B,A)
=> P(A) * P(B|A) = P(B) * P(A|B)
=> P(A|B) = P(B|A) * P(A) / P(B)
简单应用：比如有10个西瓜，西瓜有很多特征[圆/椭圆，平滑/粗糙]，根据特征训练并判断分类标签[好瓜/坏瓜]。
P(标签|特征) = P(特征|标签) * P(标签) / P(特征)

朴素贝叶斯有一个很重要的假设：条件独立性，即特征之间是独立的，这也是贝叶斯“朴素”的原因，它将问题简化了。实际生活中很多特征之间大多都是有关系的。

3. 先验概率与后验概率

先验概率：标签的概率，比如上面西瓜分类中，好瓜标签的概率。
后验概率：在特征已知的情况下发生的概率，比如特征为圆且平滑的西瓜，它是好瓜的概率。

【贝叶斯分类器基本原理】

• 贝叶斯决策论通过相关概率已知的情况下，利用误判损失来选择最优的类别分类。
  假设有N种可能的分类标记，记为Y = {c1, c2, c3, …, cN}，那对于样本x，它属于哪一类呢？计算步骤如下：
  step1：算出样本x属于第i个类别的概率，即P(ci|x)；
  step2：通过比较所有的P(ci|x)，得到样本x所属的最佳类别；
  step3：将类别ci和样本x代入贝叶斯公式中，得到：
  P(ci|x) = P(x|ci) * P(ci) / P(x)
  其中，P(ci)为先验概率，P(x|ci)为条件概率，我们需要求的就是P(x|ci)条件概率。

• 假设样本x包含d个属性，即x = {x1, x2, x3, …, xd}，那么：
  P(x|ci) = P(x1, x2, x3, …, xd|ci)
  这个联合概率难以从有限训练样本中直接计算得到。朴素贝叶斯采用“属性条件独立性假设”，即假设所有的属性是相互独立的，那么：
  P(x|ci) = P(x1, x2, x3, …, xd|ci) = P(xj|ci)的乘积

• 最终只需要对条件概率P(xj|ci)求解，即对各自特征属性的条件概率求解，按照条件概率公式，采用统计的方式求解：
  P(xj|ci) = P(xj, ci) / P(ci) = num(xj, ci) / num(ci)
  其中，num(xj, ci)表示训练样本中xj, ci同时出现的次数。

【实战案例】

西瓜训练集数据：https://download.csdn.net/download/LWY_Xing/13209988

对下面的测试数据进行分类：

计算过程：

1. 计算标签的先验概率P(ci)：
   P(好瓜=是) = 8 / 17 = 0.471
   P(好瓜=否) = 9 / 17 = 0.529
2. 计算每个特征属性的条件概率：
   青绿|是 = （色泽=青绿|好瓜=是）= 3/8 = 0.375
   青绿|否 = （色泽=青绿|好瓜=否）= 3/9 ≈ 0.333
   蜷缩|是 = （根蒂=蜷缩|好瓜=是）= 5/8 = 0.625
   蜷缩|否 = （根蒂=蜷缩|好瓜=否）= 3/9 = 0.333
   浊响|是 = （敲声=浊响|好瓜=是）= 6/8 = 0.750
   浊响|否 = （敲声=浊响|好瓜=否）= 4/9 ≈ 0.444
   清晰|是 = （纹理=清晰|好瓜=是）= 7/8 = 0.875
   清晰|否 = （纹理=清晰|好瓜=否）= 2/9 ≈ 0.222
   凹陷|是 = （脐部=凹陷|好瓜=是）= 6/8 = 0.750
   凹陷|否 = （脐部=凹陷|好瓜=否）= 2/9 ≈ 0.222
   硬滑|是 = （触感=硬滑|好瓜=是）= 6/8 = 0.750
   硬滑|否 = （触感=硬滑|好瓜=否）= 6/9 ≈ 0.667
   对于特征是连续的数据，假设他们服从正态分布，根据密度概率函数公式计算：
   ​
3. 根据以上计算结果可以看出，P(好瓜=是)=0.063 > P(好瓜=否)=6.8*10^(-5)，因此，朴素贝叶斯分类器预测的测试样本数据为“好瓜”。

【代码实现】

import math
import pandas as pd

watermelon_frame = pd.read_csv('./xigua.csv', sep=' ')
print(watermelon_frame.shape)

good_melon_num = watermelon_frame.loc[watermelon_frame['好瓜'] == '是'].shape[0]
bad_melon_num = watermelon_frame.loc[watermelon_frame['好瓜'] == '否'].shape[0]
total_num = watermelon_frame.shape[0]

prob_good_melon = round(good_melon_num / total_num, 3)
prob_bad_melon = round(bad_melon_num / total_num, 3)
print('P(好瓜 = 是) = %.3f' %(prob_good_melon))
print('P(好瓜 = 否) = %.3f' %(prob_bad_melon))

green_yes_num = watermelon_frame.loc[(watermelon_frame['色泽'] == '青绿') & (watermelon_frame['好瓜'] == '是')].shape[0]
prob_green_yes = round(green_yes_num / good_melon_num, 3)
print('P(青绿|是) = %.3f' %(prob_green_yes))
green_no_num = watermelon_frame.loc[(watermelon_frame['色泽'] == '青绿') & (watermelon_frame['好瓜'] == '否')].shape[0]
prob_green_no = round(green_no_num / bad_melon_num, 3)
print('P(青绿|否) = %.3f' %(prob_green_no))

rollup_yes_num = watermelon_frame.loc[(watermelon_frame['根蒂'] == '蜷缩') & (watermelon_frame['好瓜'] == '是')].shape[0]
prob_rollup_yes = round(rollup_yes_num / good_melon_num, 3)
print('P(蜷缩|是) = %.3f' %(prob_rollup_yes))
rollup_no_num = watermelon_frame.loc[(watermelon_frame['根蒂'] == '蜷缩') & (watermelon_frame['好瓜'] == '否')].shape[0]
prob_rollup_no = round(rollup_no_num / bad_melon_num, 3)
print('P(蜷缩|否) = %.3f' %(prob_rollup_no))

voicedsound_yes_num = watermelon_frame.loc[(watermelon_frame['敲声'] == '浊响') & (watermelon_frame['好瓜'] == '是')].shape[0]
prob_voicedsound_yes = round(voicedsound_yes_num / good_melon_num, 3)
print('P(浊响|是) = %.3f' %(prob_voicedsound_yes))
voicedsound_no_num = watermelon_frame.loc[(watermelon_frame['敲声'] == '浊响') & (watermelon_frame['好瓜'] == '否')].shape[0]
prob_voicedsound_no = round(voicedsound_no_num / bad_melon_num, 3)
print('P(浊响|否) = %.3f' %(prob_voicedsound_no))

clear_yes_num = watermelon_frame.loc[(watermelon_frame['纹理'] == '清晰') & (watermelon_frame['好瓜'] == '是')].shape[0]
prob_clear_yes = round(clear_yes_num / good_melon_num, 3)
print('P(清晰|是) = %.3f' %(prob_clear_yes))
clear_no_num = watermelon_frame.loc[(watermelon_frame['纹理'] == '清晰') & (watermelon_frame['好瓜'] == '否')].shape[0]
prob_clear_no = round(clear_no_num / bad_melon_num, 3)
print('P(清晰|否) = %.3f' %(prob_clear_no))

sunken_yes_num = watermelon_frame.loc[(watermelon_frame['脐部'] == '凹陷') & (watermelon_frame['好瓜'] == '是')].shape[0]
prob_sunken_yes = round(sunken_yes_num / good_melon_num, 3)
print('P(凹陷|是) = %.3f' %(prob_sunken_yes))
sunken_no_num = watermelon_frame.loc[(watermelon_frame['脐部'] == '凹陷') & (watermelon_frame['好瓜'] == '否')].shape[0]
prob_sunken_no = round(sunken_no_num / bad_melon_num, 3)
print('P(凹陷|否) = %.3f' %(prob_sunken_no))

hardslippery_yes_num = watermelon_frame.loc[(watermelon_frame['触感'] == '硬滑') & (watermelon_frame['好瓜'] == '是')].shape[0]
prob_hardslippery_yes = round(hardslippery_yes_num / good_melon_num, 3)
print('P(硬滑|是) = %.3f' %(prob_hardslippery_yes))
hardslippery_no_num = watermelon_frame.loc[(watermelon_frame['触感'] == '硬滑') & (watermelon_frame['好瓜'] == '否')].shape[0]
prob_hardslippery_no = round(hardslippery_no_num / bad_melon_num, 3)
print('P(硬滑|否) = %.3f' %(prob_hardslippery_no))


def prop_density_fun(x, mean, var):
    return round(math.e**(-(x - mean)**2 / (2 * var)) / math.sqrt(2 * math.pi * var), 3)

density_yes_frame = watermelon_frame.loc[watermelon_frame['好瓜'] == '是']
print(density_yes_frame)
density_yes_frame = density_yes_frame.loc[:, '密度']
density_yes_mean = round(density_yes_frame.mean(), 3)
density_yes_var = round(density_yes_frame.var(), 3)
print('density and good melon mean = %0.3f' %(density_yes_mean))
print('density and good melon var = %0.3f' %(density_yes_var))
prop_density_yes = prop_density_fun(0.697, density_yes_mean, density_yes_var)
print('P(密度=0.697|是) = %0.3f' %(prop_density_yes))

density_no_frame = watermelon_frame.loc[watermelon_frame['好瓜'] == '否']
print(density_no_frame)
density_no_frame = density_no_frame.loc[:, '密度']
density_no_mean = round(density_no_frame.mean(), 3)
density_no_var = round(density_no_frame.var(), 3)
print('density and bad melon mean = %0.3f' %(density_no_mean))
print('density and bad melon var = %0.3f' %(density_no_var))
prop_density_no = prop_density_fun(0.697, density_no_mean, density_no_var)
print('P(密度=0.697|否) = %0.3f' %(prop_density_no))

sugary_yes_frame = watermelon_frame.loc[watermelon_frame['好瓜'] == '是']
print(sugary_yes_frame)
sugary_yes_frame = sugary_yes_frame.loc[:, '含糖率']
sugary_yes_mean = round(sugary_yes_frame.mean(), 3)
sugary_yes_var = round(sugary_yes_frame.var(), 3)
print('sugary and good melon mean = %0.3f' %(sugary_yes_mean))
print('sugary and good melon var = %0.3f' %(sugary_yes_var))
prop_sugary_yes = prop_density_fun(0.460, sugary_yes_mean, sugary_yes_var)
print('P(含糖率=0.460|是) = %0.3f' %(prop_sugary_yes))

sugary_no_frame = watermelon_frame.loc[watermelon_frame['好瓜'] == '否']
print(sugary_no_frame)
sugary_no_frame = sugary_no_frame.loc[:, '含糖率']
sugary_no_mean = round(sugary_no_frame.mean(), 3)
sugary_no_var = round(sugary_no_frame.var(), 3)
print('sugary and bad melon mean = %0.3f' %(sugary_no_mean))
print('sugary and bad melon var = %0.3f' %(sugary_no_var))
prop_sugary_no = prop_density_fun(0.460, sugary_no_mean, sugary_no_var)
print('P(含糖率=0.460|否) = %0.3f' %(prop_sugary_no))


prop_good_melon_test = round(prob_green_yes * prob_rollup_yes * prob_voicedsound_yes * prob_clear_yes * prob_sunken_yes * prob_hardslippery_yes * prop_density_yes * prop_sugary_yes, 6)
prop_bad_melon_test = round(prob_green_no * prob_rollup_no * prob_voicedsound_no * prob_clear_no * prob_sunken_no * prob_hardslippery_no * prop_density_no * prop_sugary_no, 6)
print('prop good melon test = %0.6f' %(prop_good_melon_test))
print('prop bad melon test = %0.6f' %(prop_bad_melon_test))
if prop_good_melon_test > prop_bad_melon_test:
    print('test data is good melon!')
else:
    print('test data is bad melon!')

(base) k8s-master@k8s-master:~/Desktop/python/nlp_learning/class1$ python xigua_classification_by_Naive_Bayes.py
(17, 10)
P(好瓜 = 是) = 0.471
P(好瓜 = 否) = 0.529
P(青绿|是) = 0.375
P(青绿|否) = 0.333
P(蜷缩|是) = 0.625
P(蜷缩|否) = 0.333
P(浊响|是) = 0.750
P(浊响|否) = 0.444
P(清晰|是) = 0.875
P(清晰|否) = 0.222
P(凹陷|是) = 0.625
P(凹陷|否) = 0.222
P(硬滑|是) = 0.750
P(硬滑|否) = 0.667
density and good melon mean = 0.574
density and good melon var = 0.017
P(密度=0.697|是) = 1.961
density and bad melon mean = 0.496
density and bad melon var = 0.038
P(密度=0.697|否) = 1.203
sugary and good melon mean = 0.279
sugary and good melon var = 0.010
P(含糖率=0.460|是) = 0.775
sugary and bad melon mean = 0.154
sugary and bad melon var = 0.012
P(含糖率=0.460|否) = 0.074
prop good melon test = 0.109572
prop bad melon test = 0.000144
test data is good melon!

【朴素贝叶斯优缺点】

• 优点：

1. 时空开销都非常小；
2. 训练预测的时间开销都小；

• 缺点：

1. 简化的假设；

• 对样本的适配性质：

1. 大样本更好；

【总结】后验概率最大化

1. 比较P(label=1|特征)和P(label=0|特征)，谁大选择谁；
2. 使用朴素贝叶斯公式，反求：
   P(特征|label=1) * P(label=1) / P(特征)
   P(特征|label=0) * P(label=0) / P(特征)
3. 根据条件独立性假设，拆分特征的联合概率计算方式：
   假设有3个特征，根据联合概率公式：
   P(特征) = P(特征1) * P(特征2|特征1) * P(特征3|特征1, 特征2)
   根据条件独立性假设化简：
   P(特征) = P(特征1) * P(特征2) * P(特征3)
4. 训练预测阶段做什么?
   训练：生成统计概率值
   预测：直接带入公式计算

【相关面试问题】

1. 训练和预测阶段都做了什么？
   训练：生成统计概率值；
   预测：直接带入公式计算；
2. 朴素贝叶斯中“朴素”的含义是什么？
   条件独立性的假设。
3. 针对朴素贝叶斯公式，为什么不需要计算分母P(特征)？
   因为分母是一个常量。
4. 如果特征是连续值，还能用吗？如果可以使用什么方式？
   a. 采用分桶离散化：等距分桶，等频分桶，至于怎么选择需要看实验结果；
   b. 采用正态分布-高斯分布估计，比如上面计算西瓜含糖率的概率：
   
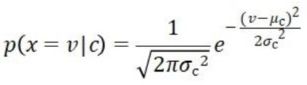
   概率密度函数的输入是连续型的随机变量，输出是对应的概率。
5. 概率的拉普拉斯平滑
   防止0概率的连乘法效应。
6. 朴素贝叶斯有哪些模型？
   a. GaussianNB：先验为高斯分布的朴素贝叶斯；
   b. MultinomialNB：先验为多项式分布的朴素贝叶斯；
   c. BernoulliNB：先验为伯努利分布的朴素贝叶斯；
   这三个类适用的分类场景各不相同：
   a. 一般来说，如果样本特征的分布大部分是连续值，使用GaussianNB会比较好；
   b. 如果如果样本特征的分大部分是多元离散值，使用MultinomialNB比较合适；
   c. 如果样本特征是二元离散值或者很稀疏的多元离散值，应该使用BernoulliNB；