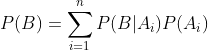机器学习实战——朴素贝叶斯

目录

一、朴素贝叶斯理论

1.概述

2.朴素贝叶斯特点

3.贝叶斯决策理论

4.条件概率与全概率公式

5.贝叶斯推断

二、朴素贝叶斯分类器应用

拉普拉斯修正

三、垃圾邮件分类

---

一、朴素贝叶斯理论

1.概述

        朴素贝叶斯算法是有监督的学习算法，解决的是分类问题。其分类原理就是利用贝叶斯公式根据某特征的先验概率计算出其后验概率，然后选择具有最大后验概率的类作为该特征所属的类。之所以称之为”朴素”，是因为贝叶斯分类只做最原始、最简单的假设：所有的特征之间是统计独立的。但由于该算法以自变量之间的独立（条件特征独立）性和连续变量的正态性假设为前提，就会导致算法精度在某种程度上受影响。

2.朴素贝叶斯特点

优点：

1. 对小规模的数据表现很好，能个处理多分类任务，适合增量式训练(即可以实时的对新增的样本进行训练)
2. 朴素贝叶斯模型发源于古典数学理论，有稳定的分类效率
3. 朴素贝叶斯算法的健壮性比较好，对于不同类型的数据集不会呈现出太大的差异性

缺点：

1. 由于是通过先验概率和数据来决定后验的概率从而决定分类，所以分类决策存在一定的错误率
2. 对输入数据的表达形式较敏感
3. 数据集属性的独立性在很多情况下是很难满足的，因为数据集的属性之间往往都存在着相互关联，在属性个数比较多或者属性之间相关性较大时，分类效果不好

3.贝叶斯决策理论

        朴素贝叶斯是贝叶斯决策理论的一部分，所以有必要了解一下贝叶斯决策理论。假设有一个数据集，它由两类数据组成，如下图：

我们现在用p1(x,y)表示数据点(x,y)属于类别1(图中红色圆点表示的类别)的概率，用p2(x,y)表示数据点(x,y)属于类别2(图中蓝色三角形表示的类别)的概率，那么对于一个新数据点(x,y)，可以用下面的规则来判断它的类别：

• 如果p1(x,y) > p2(x,y)，那么类别为1
• 如果p1(x,y) < p2(x,y)，那么类别为2

也就是说，我们会选择高概率对应的类别。这就是贝叶斯决策理论的核心思想，即选择具有最高概率的决策。

4.条件概率与全概率公式

        条件概率，就是指在事件B发生的情况下，事件A发生的概率，用P(A|B)来表示。若只有两个事件A， B， 那么：

那么：

---

        全概率公式，指若事件{A1，A2，…，An}构成一个完备事件组且都有正概率，则对任意一个事件B都有：

则有：

5.贝叶斯推断

        对条件概率公式进行变形，可以得到如下形式：

把P(A)称为先验概率(Prior probability)，即在B事件发生之前，我们对A事件概率的一个判断。

P(A|B)称为后验概率(Posterior probability)，即在B事件发生之后，我们对A事件概率的重新评估。

P(B|A)/P(B)称为可能性函数(Likelyhood)，这是一个调整因子，使得预估概率更接近真实概率。

所以条件概率可以理解为：后验概率 = 先验概率 × 调整因子

如果"可能性函数">1，意味着先验概率被增强，事件A的发生的可能性变大；
如果"可能性函数"=1，意味着B事件无助于判断事件A的可能性；
如果"可能性函数"<1，意味着"先验概率"被削弱，事件A的可能性变小。

二、朴素贝叶斯分类器应用

        用西瓜数据集训练一个朴素贝叶斯分类器，对如下测试例进行分类。

下图是17颗西瓜的数据：

 可以求出：

P(好瓜)=8/17=0.471，P(坏瓜)=9/17=0.529

P(色=青|好)=3/8=0.375，P(色=青|坏)=3/9=0.333

P(根=卷|好)=5/8=0.625，P(根=卷|坏)=3/9=0.333

P(敲=浊|好)=6/8=0.75，P(敲=浊|坏)=4/9=0.444

P(纹=清|好)=7/8=0.875，P(纹=清|坏)=2/9=0.222

P(脐=凹|好)=5/8=0.625，P(脐=凹|坏)=2/9=0.222

P(触=硬|好)=6/8=0.75，P(触=硬|坏)=6/9=0.667

P(密度=0.697|好瓜)=1.959，P(密度=0.697|坏瓜)=1.203

P(糖度=0.46|好瓜)=0.788，P(糖度=0.46|坏瓜)=0.066

P(好瓜|色=青，根=卷，敲=浊，纹=清，脐=凹，触=硬，密度=0.697，糖度=0.46)=

P(坏瓜|色=青，根=卷，敲=浊，纹=清，脐=凹，触=硬，密度=0.697，糖度=0.46)=

最终结论为：好瓜

---

拉普拉斯修正

        若某个属性值在训练集中没有与某个类同时出现过，则训练后的模型会出现over-fitting现象。比如“敲声=清脆”测试例，训练集中没有该样例，因此连乘式计算的概率值为0，无论其他属性上明显像好瓜，分类结果都是“好瓜=否”，这显然不合理。为了避免其他属性携带的信息，被训练集中未出现的属性值“抹去”，在估计概率值时通常要进行拉普拉斯修正。

令n表示训练集中出现的类别数，表示第i个属性值可能类别数，则贝叶斯公式可修正为：

三、垃圾邮件分类

使用朴素贝叶斯对电子邮件进行分类的步骤：

• 收集数据：提供文本文件。
• 准备数据：将文本文件解析成词条向量。
• 分析数据：检查词条确保解析的正确性。
• 训练算法：使用我们之前建立的trainNB0()函数。
• 测试算法：使用classifyNB()，并构建一个新的测试函数来计算文档集的错误率。
• 使用算法：构建一个完整的程序对一组文档进行分类，将错分的文档输出到屏幕上。

 数据集中有两个文件夹ham和spam，spam文件下的txt文件为垃圾邮件。

---

对于英文文本，我们可以以非字母、非数字作为符号进行切分，使用split函数即可。编写代码如下：

# -*- coding: UTF-8 -*-
import re

#函数说明:接收一个大字符串并将其解析为字符串列表
def textParse(bigString):                                                   #将字符串转换为字符列表
    listOfTokens = re.split(r'\W', bigString)                              #将特殊符号作为切分标志进行字符串切分，即非字母、非数字
    return [tok.lower() for tok in listOfTokens if len(tok) > 2]            #除了单个字母，例如大写的I，其它单词变成小写


#函数说明:将切分的实验样本词条整理成不重复的词条列表，也就是词汇表
def createVocabList(dataSet):
    vocabSet = set([])                      #创建一个空的不重复列表
    for document in dataSet:               
        vocabSet = vocabSet | set(document) #取并集
    return list(vocabSet)

if __name__ == '__main__':
    docList = []; classList = []
    for i in range(1, 26):                                                  #遍历25个txt文件
        wordList = textParse(open('email/spam/%d.txt' % i, 'r').read())     #读取每个垃圾邮件，并字符串转换成字符串列表
        docList.append(wordList)
        classList.append(1)                                                 #标记垃圾邮件，1表示垃圾文件
        wordList = textParse(open('email/ham/%d.txt' % i, 'r').read())      #读取每个非垃圾邮件，并字符串转换成字符串列表
        docList.append(wordList)
        classList.append(0)                                                 #标记非垃圾邮件，1表示垃圾文件   
    vocabList = createVocabList(docList)                                    #创建词汇表，不重复
    print(vocabList)

得到词汇表，如下图：

根据词汇表，我们就可以将每个文本向量化。我们将数据集分为训练集和测试集，使用交叉验证的方式测试朴素贝叶斯分类器的准确性。编写代码如下：

# -*- coding: UTF-8 -*-
import numpy as np
import random
import re

#函数说明:将切分的实验样本词条整理成不重复的词条列表，也就是词汇表
def createVocabList(dataSet):
    vocabSet = set([])                      #创建一个空的不重复列表
    for document in dataSet:
        vocabSet = vocabSet | set(document) #取并集
    return list(vocabSet)


#函数说明:根据vocabList词汇表，将inputSet向量化，向量的每个元素为1或0
def setOfWords2Vec(vocabList, inputSet):
    returnVec = [0] * len(vocabList)                                    #创建一个其中所含元素都为0的向量
    for word in inputSet:                                                #遍历每个词条
        if word in vocabList:                                            #如果词条存在于词汇表中，则置1
            returnVec[vocabList.index(word)] = 1
        else: print("the word: %s is not in my Vocabulary!" % word)
    return returnVec                                                    #返回文档向量



#函数说明:根据vocabList词汇表，构建词袋模型
def bagOfWords2VecMN(vocabList, inputSet):
    returnVec = [0]*len(vocabList)                                        #创建一个其中所含元素都为0的向量
    for word in inputSet:                                                #遍历每个词条
        if word in vocabList:                                            #如果词条存在于词汇表中，则计数加一
            returnVec[vocabList.index(word)] += 1
    return returnVec                                                    #返回词袋模型


#函数说明:朴素贝叶斯分类器训练函数
def trainNB0(trainMatrix,trainCategory):
    numTrainDocs = len(trainMatrix)                            #计算训练的文档数目
    numWords = len(trainMatrix[0])                            #计算每篇文档的词条数
    pAbusive = sum(trainCategory)/float(numTrainDocs)        #文档属于侮辱类的概率
    p0Num = np.ones(numWords); p1Num = np.ones(numWords)    #创建numpy.ones数组,词条出现数初始化为1，拉普拉斯平滑
    p0Denom = 2.0; p1Denom = 2.0                            #分母初始化为2,拉普拉斯平滑
    for i in range(numTrainDocs):
        if trainCategory[i] == 1:                            #统计属于侮辱类的条件概率所需的数据，即P(w0|1),P(w1|1),P(w2|1)···
            p1Num += trainMatrix[i]
            p1Denom += sum(trainMatrix[i])
        else:                                                #统计属于非侮辱类的条件概率所需的数据，即P(w0|0),P(w1|0),P(w2|0)···
            p0Num += trainMatrix[i]
            p0Denom += sum(trainMatrix[i])
    p1Vect = np.log(p1Num/p1Denom)                            #取对数，防止下溢出
    p0Vect = np.log(p0Num/p0Denom)
    return p0Vect,p1Vect,pAbusive                            #返回属于侮辱类的条件概率数组，属于非侮辱类的条件概率数组，文档属于侮辱类的概率


#函数说明:朴素贝叶斯分类器分类函数
def classifyNB(vec2Classify, p0Vec, p1Vec, pClass1):
    p1 = sum(vec2Classify * p1Vec) + np.log(pClass1)        #对应元素相乘。logA * B = logA + logB，所以这里加上log(pClass1)
    p0 = sum(vec2Classify * p0Vec) + np.log(1.0 - pClass1)
    if p1 > p0:
        return 1
    else:
        return 0


#函数说明:朴素贝叶斯分类器训练函数
def trainNB0(trainMatrix,trainCategory):
    numTrainDocs = len(trainMatrix)                            #计算训练的文档数目
    numWords = len(trainMatrix[0])                            #计算每篇文档的词条数
    pAbusive = sum(trainCategory)/float(numTrainDocs)        #文档属于侮辱类的概率
    p0Num = np.ones(numWords); p1Num = np.ones(numWords)    #创建numpy.ones数组,词条出现数初始化为1，拉普拉斯平滑
    p0Denom = 2.0; p1Denom = 2.0                            #分母初始化为2,拉普拉斯平滑
    for i in range(numTrainDocs):
        if trainCategory[i] == 1:                            #统计属于侮辱类的条件概率所需的数据，即P(w0|1),P(w1|1),P(w2|1)···
            p1Num += trainMatrix[i]
            p1Denom += sum(trainMatrix[i])
        else:                                                #统计属于非侮辱类的条件概率所需的数据，即P(w0|0),P(w1|0),P(w2|0)···
            p0Num += trainMatrix[i]
            p0Denom += sum(trainMatrix[i])
    p1Vect = np.log(p1Num/p1Denom)                            #取对数，防止下溢出
    p0Vect = np.log(p0Num/p0Denom)
    return p0Vect,p1Vect,pAbusive                            #返回属于侮辱类的条件概率数组，属于非侮辱类的条件概率数组，文档属于侮辱类的概率

#函数说明:接收一个大字符串并将其解析为字符串列表
def textParse(bigString):                                                   #将字符串转换为字符列表
    listOfTokens = re.split(r'\W', bigString)                              #将特殊符号作为切分标志进行字符串切分，即非字母、非数字
    return [tok.lower() for tok in listOfTokens if len(tok) > 2]            #除了单个字母，例如大写的I，其它单词变成小写

#函数说明:测试朴素贝叶斯分类器
def spamTest():
    docList = []; classList = []; fullText = []
    for i in range(1, 26):                                                  #遍历25个txt文件
        wordList = textParse(open('email/spam/%d.txt' % i, 'r').read())     #读取每个垃圾邮件，并字符串转换成字符串列表
        docList.append(wordList)
        fullText.append(wordList)
        classList.append(1)                                                 #标记垃圾邮件，1表示垃圾文件
        wordList = textParse(open('email/ham/%d.txt' % i, 'r').read())      #读取每个非垃圾邮件，并字符串转换成字符串列表
        docList.append(wordList)
        fullText.append(wordList)
        classList.append(0)                                                 #标记非垃圾邮件，1表示垃圾文件
    vocabList = createVocabList(docList)                                    #创建词汇表，不重复
    trainingSet = list(range(50)); testSet = []                             #创建存储训练集的索引值的列表和测试集的索引值的列表
    for i in range(10):                                                     #从50个邮件中，随机挑选出40个作为训练集,10个做测试集
        randIndex = int(random.uniform(0, len(trainingSet)))                #随机选取索索引值
        testSet.append(trainingSet[randIndex])                              #添加测试集的索引值
        del(trainingSet[randIndex])                                         #在训练集列表中删除添加到测试集的索引值
    trainMat = []; trainClasses = []                                        #创建训练集矩阵和训练集类别标签系向量
    for docIndex in trainingSet:                                            #遍历训练集
        trainMat.append(setOfWords2Vec(vocabList, docList[docIndex]))       #将生成的词集模型添加到训练矩阵中
        trainClasses.append(classList[docIndex])                            #将类别添加到训练集类别标签系向量中
    p0V, p1V, pSpam = trainNB0(np.array(trainMat), np.array(trainClasses))  #训练朴素贝叶斯模型
    errorCount = 0                                                          #错误分类计数
    for docIndex in testSet:                                                #遍历测试集
        wordVector = setOfWords2Vec(vocabList, docList[docIndex])           #测试集的词集模型
        if classifyNB(np.array(wordVector), p0V, p1V, pSpam) != classList[docIndex]:    #如果分类错误
            errorCount += 1                                                 #错误计数加1
            print("分类错误的测试集：",docList[docIndex])
    print('错误率：%.2f%%' % (float(errorCount) / len(testSet) * 100))

if __name__ == '__main__':
    spamTest()

运行结果： 

        函数spamTest()会输出在10封随机选择的电子邮件上的分类错误概率。既然这些电子邮件是随机选择的，所以每次的输出结果可能有些差别。如果发现错误的话，函数会输出错误的文档的此表，这样就可以了解到底是哪篇文档发生了错误。如果想要更好地估计错误率，那么就应该将上述过程重复多次，比如说10次，然后求平均值。相比之下，将垃圾邮件误判为正常邮件要比将正常邮件归为垃圾邮件好。