从0开始，搞懂SVM支持向量机！

SVM支持向量机：

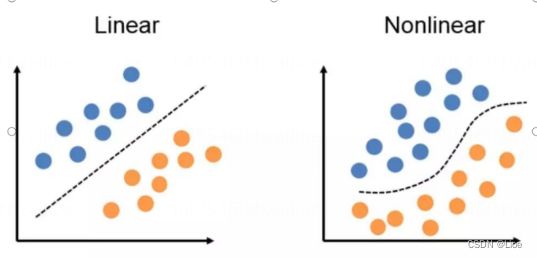
支持向量机(Support Vecor. Machine, SVM)本身是一个二元分类算法，是对感知器算法模型的一种扩展，现在的SVM算法支持线性分类和非线性分类的分类应用，并且也能够直接将SVM应用于回归应用中，同时通过OvR,或者OvO的方式我们也可以将SVM应用在多元分类领域中。在不考虑集成学习算法，不考虑特定的数据集的时候，在分类算法中SVM可以说是特别优秀的。

感知机（SVM支持向量机基础）：

在任意空间中，感知机模型寻找的就是一个超平面，能够把所有的二元类别分割开。感知机模型的前提是：数据是线性可分的。

对应m个样本，每个样本n维特征以及一个二元类别输出y,如下：
$$[(x_1^{(1)},x_2^{(1)},...,x_n^{(1)}),(x_1^{(2)},x_2^{(2)},...,x_n^{(2)}),...,(x_1^{(m)},x_2^{(m)},...,x_n^{(m)})]$$
目的是找到一个超平面
$$w_0+w_1{x}_1+...+w_n{x}_n=0\to wX=0$$
让一个类别的样本满足：$wx>0$ ；另外一个类别的满足：$wx<0$ (这里就是带一个样本数据进入平面中，根据得到的值进行分类)

因此，感知机模型为**(把正1作为正例，负1作为负例)**：
$$y=sign(wx)=\{\begin{array}{ll}1& \text{ if }wx>0\\ -1& \text{ if }wx<0\end{array}$$
感知机分类的损失函数：

期望使分类错误的所有样本到超平面的距离之和最小。

逻辑回归的几何意义，又何尝不是向量空间找到一个超平面，超平面一侧的点计算分数结果为负，另一侧结果分数为正，只不过最后不直接看sign符合，而是根据sigmoid,函数将分数映射到0-1之间通过最大似然来赋予概率意义。

补充一下点到空间的距离公式**(空间距离公式，($x_0,y_0$) )：
$$\begin{gathered} d(w{x}_0)=\frac{|w^T{x}_0+b|}{||w||} \\ 其中，||w||=\sqrt{w^{T}w} \end{gathered}$$
在感知机模型中，对于那些正确分类的点**，$y_0$ 必然与 $|w^T{x}_0+b|$ 同号，所以我们可以定义一个距离：几何距离
$$\gamma =\frac{y_0(w^T{x}_0+b)}{||w||}$$
那么当一个空间固定时，$||w||$就已经固定了，我们用一个相对距离来表示点到空间的距离：函数距离
$${\gamma }^{{}^{\prime }}=y_0(w^T{x}_0+b)$$
回到上文：期望使分类错误的所有样本到超平面的距离之和最小

那么,我们利用SGD来求解损失函数的过程为：
$$\begin{gathered} MSE:L=-\sum _{i=1}^m{y}^{(i)}{w}^T{x}^{(i)} \\ \frac{\delta L(w)}{\delta w}=-\sum _{i=1}^m{y}^{(i)}{x}^{(i)} \\ {w}^{k+1}=w^k+\alpha y^{(i)}{x}^{(i)} \end{gathered}$$

---

SVM算法思想：

与感知机相同的地方：

SVM也是通过寻找超平面，用于解决二分类问题的分类算法。超平面一侧的点计算分数结果为负是负例，另一侧结果分数为正是正例。与感知机相同，通过sign给出预测标签，正例为+1，负例为-1，模型判别式同样：
$$y=sign(wx)=\{\begin{array}{ll}1& \text{ if }wx>0\\ -1& \text{ if }wx<0\end{array}$$
不同的地方：

损失函数与感知机和逻辑回归都不同。

感知机是通过判错点找超平面，逻辑回归是通过最大似然寻找超平面，SVM是通过支持向量寻找超平面。

高级的地方：

明显是中间这条分界更好，如何找到这条分界线，这便是SVM要解决的问题。

在感知器模型中，我们可以找到多个可以分类的超平面将数据分开，并且优化时希望所有的点都离超平面尽可能的远，但是实际上离超平面足够远的点基本上都是被正确分类的，所以这个是没有意义的; 反而比较关心那些离超平面很近的点，这些点比较容易分错。

所以SVM企图找到一个边界（超平面）。在支持向量机中，距离超平面最近的且满足一定条件的几个训练样本点被称为支持向量。SVM最终目的就是这些离超平面的点越远越好。

---

SVM支持向量机分类：

间隔：数据点到分割超平面的距离称为间隔。

支持向量：离分割超平面最近的那些点叫做支持向量

1.线性可分支持向量机：

损失函数：

线性可分：在数据集中，如果可以找出一个超平面，将两组数据分开，那么这个数据集叫做线性可分数据。

硬间隔最大化：

需要找到一个超平面

1.能够完美分类正负例

2.距离最近的点越远越好

超平面怎么确定

1.$\hat{y}=sign(w^{T}x+b)$

2.$w^{T}x+b=0$表示的就是分割超平面

3.只要确认了$w$和$b$，就确定了我们的分割超平面

目标：

能正确分类的平面中，距离越近的点越远越好，即：找到一组最好的w和b固定一个超平面，使这个超平面在能完美区分正负例的基础上，距离最近的点间隔最大

转换为有约束的函数最优化问题就是:
$$\begin{gathered} ma{x}_{w,b}{\gamma }_{min}=\frac{y_{min}(w{x}_{min+b})}{||w||} \\ s.t{y}_i(w^T{x}_i+b)={\gamma }^{(i)}⩾{\gamma }^{min} \end{gathered}$$

简化目标：

我们设定一个阈值：令${\gamma }^{min}=1$,那么最优化问题就简述成：
$$\begin{gathered} max\frac{1}{||w|{|}_2} \\ s.t{y}_i(w^T{x}_i+b)={\gamma }^{(i)}⩾1 \end{gathered}$$

等价于：
$$\begin{gathered} max\frac{1}{2}||w|{|}_2 \\ s.t{y}_i(w^T{x}_i+b)={\gamma }^{(i)}⩾1 \end{gathered}$$
可以简化的原因：一组$w,b$只能固定一个超平面，一个超平面对应无数个$w,b$。那么我们只需要找到一个$w$，就可以找到这个超平面，因此我们选择最好求的，${\gamma }^{{}^{\prime }}=1$

因此损失函数为：
$$\begin{gathered} min\frac{1}{2}||w|{|}_2 \\ s.t{y}_i(w^T{x}_i+b)=1 \end{gathered}$$

---

SVM训练原理：

SVM的训练原理其实就是对损失函数进行最优化求解（最值求解）的过程。

我们的求解目标就是求得一个分割超平面，也就是求解一组$w,b$

---

下面先讲述一下最优化的数学基础：

带约束条件的最优化问题泛化表示方法：
$$\begin{gathered} \underset{x\in R}{\min }f(x) \\ s.t.c_i\le 0,i=1,2,...,k \\ {h}_j(x)=0,j=1,2,...,l \end{gathered}$$
可以将约束条件表述成k个不等式约束条件，和L个等式约束条件，我们将其命名为原始最优化问题。

拉格朗日函数：

定义某原始最优化问题的拉格朗日函数为：
$$L(x,\alpha ,\beta )=f(x)+\sum _{i=1}^k{\alpha }_i{c}_i(x)+\sum _{i=1}^l{\beta }_j{h}_j(x)$$
其中$c_i$是第i个不等式约束函数，$b_j$是第j个等式约束函数。

${\alpha }_i$和${\beta }_i$是拉格朗日乘子

拉格朗日函数的特性：

令${\theta }_P(x)$
$$=\underset{\alpha ,\beta ;{\alpha }_i\ge 0}{\max }L(x,\alpha ,\beta )$$
若x不满足在原始最优化问题中的条件：
$${\theta }_P(x)=\underset{\alpha ,\beta ;{\alpha }_i\ge 0}{\max }[f(x)+\sum _{i=1}^k{\alpha }_i{c}_i(x)+\sum _{j=1}^l{\beta }_j{h}_j(x)]=+\infty$$
若x满足在原始最优化问题中的条件：
$${\theta }_P(x)=f(x)$$
其实也是可以理解的，如果满足约束条件，那么$h_j(x)=0$。又因为$c_i\le 0,{\alpha }_i\ge 0$,所以${\sum }_{i=1}^k{\alpha }_i{c}_i(x)$肯定为负。

因此$\underset{\alpha ,\beta ;{\alpha }_i\ge 0}{\max }L(x,\alpha ,\beta )$时，${\sum }_{i=1}^k{\alpha }_i{c}_i(x)=0$,所以${\theta }_P(x)=f(x)$

那么回到我们的最优化问题中来：
$$\begin{gathered} \underset{x\in R}{\min }f(x) \\ s.t.c_i\le 0,i=1,2,...,k \\ {h}_j(x)=0,j=1,2,...,l \end{gathered}$$
在x满足条件的情况下
$$minf(x)=min{\theta }_P(x)=\underset{x}{\min }\underset{\alpha ,\beta ;{\alpha }_i\ge 0}{\max }L(x,\alpha ,\beta )$$
以上三个拥有同样的解！因此我们定义原始问题的最优解为$p^{\ast }=\underset{x}{\min }{\theta }_P(x)$

对偶问题：

当$f(x)$和$c_i$函数均为凸函数，$h_j$函数为仿射函数时，有可以使用拉格朗日的对偶形式：
$$\underset{x}{\min }\underset{\alpha ,\beta ;{\alpha }_i\ge 0}{\max }L(x,\alpha ,\beta )=\underset{\alpha ,\beta ;{\alpha }_i\ge 0}{\max }\underset{x}{\min }L(x,\alpha ,\beta )$$
设 $\underset{\alpha ,\beta ;{\alpha }_i\ge 0}{\max }\underset{x}{\min }L(x,\alpha ,\beta )$ 的解为 $x^{\ast },{\alpha }^{\ast },{\beta }^{\ast }$则：
$$p^{\ast }=(x^{\ast },{\alpha }^{\ast },{\beta }^{\ast })$$
KKT条件：
$$\begin{gathered} a_i^{\ast }{c}_i^{\ast }=0,i=1,2,...,k \\ {c}_i(x^{\ast })\le 0,i=1,2,...,k \\ {\alpha }_i^{\ast }\ge 0,i=1,2,...,k \\ {h}_j(x^{\ast })=0,j=1,2,...,l \end{gathered}$$

$$\begin{gathered} {\nabla }_a对a求梯度(偏导) \\ {\nabla }_{x}L(x^{\ast },{\alpha }^{\ast },{\beta }^{\ast })=0 \\ {\nabla }_{\alpha }L(x^{\ast },{\alpha }^{\ast },{\beta }^{\ast })=0 \\ {\nabla }_{\beta }L(x^{\ast },{\alpha }^{\ast },{\beta }^{\ast })=0 \end{gathered}$$

先做一个小总结，我们上面讲述了

1.拉格朗日函数

2.对偶问题

3.KKT条件

这三个部分都是我们对SVM的损失函数进行最优化的基础

---

对于我们的SVM中的原始问题：有约束的最优化问题
$$\begin{gathered} min\frac{1}{2}||w|{|}_2 \\ s.t{y}_i(w^T{x}_i+b)=1 \end{gathered}$$
构建拉格朗日函数**(我们假设一共有m条样本，每个样本有n个特征)**：
$$\begin{gathered} L(w,b,\alpha )=\frac{1}{2}||w|{|}_2^2-\sum _{i=1}^m{\alpha }_i[y_i(w^T{x}_i+b)-1],{\alpha }_i\ge 0 \\ 我们假设L(w,b,\alpha )的解为(w^{\ast },b^{\ast },{\alpha }^{\ast }) \end{gathered}$$
可将原始的有约束的最优化问题，转换成对拉格朗日函数进行无约束的最优化问题（也叫二次规划问题）

---

首先我们必须明白我们要求解的分割超平面为什么：
$$W^{\ast T}x+b^{\ast }=0$$
那么拉格朗日函数到底能求解出什么：$w^{\ast },b^{\ast },{\alpha }^{\ast }$

那么这三者之间有没有什么关系呢？

$w^{\ast }$和${\alpha }^{\ast }$:

对$L(w^{\ast },b^{\ast },{\alpha }^{\ast })$求$w^{\ast }$偏导,得
$$w^{\ast }=\sum _{i=1}^m{a}_i^{\ast }{y}_i{x}_i$$
$b^{\ast }$和${\alpha }^{\ast }$:

对于任意支持向量$(x_s,y_s)$，有：
$$y_s(w^T{x}_s+b)=y_s(\sum _{i=1}^m{a}_i{y}_i{x}_i^T{x}_s+b)=1$$
如何找到支持向量？根据KKT条件$a_i^{\ast }{c}_i^{\ast }=0$有：
$$a_i^{\ast }(y_i(w^T{x}_i+b)-1)=0,a_i^{\ast }\ge 0$$
那么当${\alpha }^{\ast }>0$时，后面一项需要$=0$，也就是
$$y_i(w^T{x}_i+b)=1$$
上面的式子意味着第i条样本$x_i$恰好在分割超平面的边上，因此$x_i$就是支持向量。

因此，我们只需要寻找${\alpha }_i^{\ast }>0$对应的样本即可，这些样本就是支持向量。

求b的过程：求出${\alpha }^{\ast }$,通过${\alpha }^{\ast }$找到所有个支持向量带进去求出所有的$b$,然后求平均，得到$b^{\ast }$

因此，我们仅需要求出${\alpha }^{\ast }$即可！

---

对于原始函数：

$x=(w,b)$,$\alpha$存在，$\beta$不存在，因此$L(x,\alpha ,\beta )$ 就写为$L(w,\alpha ,\beta )$
$$min\frac{1}{2}||w|{|}_2=min{\theta }_P(x)=\underset{w,b}{\min }\underset{\alpha ;{\alpha }_i\ge 0}{\max }L(w,\alpha ,\beta )$$
那么对偶函数为：
$$\underset{\alpha \ge 0}{\max }\underset{w,b}{\min }L(w,b,\alpha )$$
因此我们先对$L$求极小，在求极大。

求极小：
$$\begin{gathered} L(w,b,\alpha )=\frac{1}{2}||w|{|}_2^2-\sum _{i=1}^m{\alpha }_i[y_i(w^T{x}_i+b)-1],{\alpha }_i\ge 0 \\ \frac{\partial L}{\partial w}=0\to w=\sum _{i=1}^m{a}_i{y}_i{x}_i\frac{\partial L}{\partial b}=0\to \sum _{i=1}^m{a}_i{y}_i=0 \end{gathered}$$
可以看出：我们已经求出了$w$和$\alpha$的关系，下一步将$w$反代回原来的拉格朗日函数中就可以进行第二步求关于$\alpha$的极大了。
$$\begin{gathered} =\frac{1}{2}||w|{|}_2^2-\sum _{i=1}^m{\alpha }_i[y_i(w^T{x}_i+b)-1] \\ =\frac{1}{2}{w}^{T}w-\sum _{i=1}^m{\alpha }_i{y}_i{w}^T{x}_i-\sum _{i=1}^m{\alpha }_i{y}_{i}b+\sum _{i=1}^m{\alpha }_i \\ =\frac{1}{2}{w}^T\sum _{i=1}^m{\alpha }_i{y}_i{x}_i-\sum _{i=1}^m{\alpha }_i{y}_i{w}^T{x}_i-\sum _{i=1}^m{\alpha }_i{y}_{i}b+\sum _{i=1}^m{\alpha }_i \\ =-\frac{1}{2}{w}^T\sum _{i=1}^m{\alpha }_i{y}_i{x}_i-\sum _{i=1}^m{\alpha }_i{y}_{i}b+\sum _{i=1}^m{\alpha }_i \\ =-\frac{1}{2}{w}^T\sum _{i=1}^m{\alpha }_i{y}_i{x}_i-b\sum _{i=1}^m{\alpha }_i{y}_i+\sum _{i=1}^m{\alpha }_i \\ =-\frac{1}{2}(\sum _{i=1}^m{\alpha }_i{y}_i{x}_i{)}^T\sum _{i=1}^m{\alpha }_i{y}_i{x}_i-b\sum _{i=1}^m{\alpha }_i{y}_i+\sum _{i=1}^m{\alpha }_i \\ 因为{\alpha }_i,y_i是一个数，并且{\alpha }_i{y}_i=0,所以 \\ =-\frac{1}{2}\sum _{i=1}^m{\alpha }_i{y}_i{x}_i^T\sum _{i=1}^m{\alpha }_i{y}_i{x}_i+\sum _{i=1}^m{\alpha }_i \\ =-\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{y}_i{x}_i^T{\alpha }_j{y}_j{x}_j+\sum _{i=1}^m{\alpha }_i \end{gathered}$$
通过数学求解，最后得到的求极大形式为：
$$\begin{gathered} \underset{a}{\max }-\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j(x_i\cdot x_j)+\sum _{i=1}^m{\alpha }_i \\ s.t.\sum _{i=1}^m{a}_i{y}_i=0 \\ {a}_i\ge 0i=1,2,...,m \end{gathered}$$
将求极大形式“去掉负号“转换成求极小问题：
$$\begin{gathered} \underset{a}{\max }\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j(x_i\cdot x_j)-\sum _{i=1}^m{\alpha }_i \\ s.t.\sum _{i=1}^m{a}_i{y}_i=0 \\ {a}_i\ge 0i=1,2,...,m \end{gathered}$$
只要解决了上述这个问题，SVM的训练问题就完成了！$x_i,x_j,y_i,y_j$均为已知。我们通常使用SMO算法进行求解，可以求得一组${\alpha }^{\ast }$使得函数最优化。

训练流程总结：

1.原始目标：求一组$w,b$使得分隔最大

2.转换目标：利用拉格朗日函数构建目标函数，并分析得到${\alpha }^{\ast }和b^{\ast }和w^{\ast }$之间的关系。
$$\begin{gathered} \underset{a}{\max }\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j(x_i\cdot x_j)-\sum _{i=1}^m{\alpha }_i \\ s.t.\sum _{i=1}^m{a}_i{y}_i=0 \\ {a}_i\ge 0i=1,2,...,m \end{gathered}$$
3.利用SMO算法求得m个$a^{\ast }$

4.利用求得的$a^{\ast }$得到$w^{\ast }$和$b^{\ast }$
$$\begin{gathered} w^{\ast }=\sum _{i=1}^m{a}_i^{\ast }{y}_i{x}_i \\ {b}_s^{\ast }=y_s-\sum _{i=1}^m{a}_i^{\ast }{y}_i{x}_i^T{x}_s \\ {b}^{\ast }=\frac{1}{S}\sum _{i=1}^S{b}_s^{\ast } \end{gathered}$$

2.线性支持向量机：

**线性不可分：**在数据集中，没法找出一个超平面，能够将两组数据分开，那么这个数据集就叫做线性不可分数据。分割超平面:将数据集分割开来的直线/平面叫做分割超平面。

对于上面的”线性不可分”的情况，往往是由噪声点造成的。

软间隔最大化：

对于之前讲述的“线性可分SVM”，可通过构造超平面令硬间隔最大化，从而求得最好的分隔超平面。

但当存在噪声点，硬间隔不可分的情况，就不能够使用上面的“线性可分SVM”

因此我们提出一个松弛变量${\epsilon }_i>0$(每个数据点自己有一个${\epsilon }_i$)

我们将约束条件放松为：
$$y_i(w\cdot x_i+b)\ge 1-{\epsilon }_i$$
这样就至少肯定有足够的$w,b$满足条件，但是这也相当于我们没有了约束条件，只要$\epsilon$无穷大，那么所有的$w,b$都满足条件。

$\epsilon$表示异常点嵌入间隔面的深度。因此，我们需要在能选出符合约束条件的最好的$w,b$的同时，让嵌入间隔面的总深度越少越好。

损失函数以及最值优化（流程和硬间隔类似）：

损失函数：
$$\begin{gathered} min\frac{1}{2}||w|{|}_2^2+C\sum _{i=1}^m{\epsilon }_i \\ s.t.y_i(w^T{x}_i+b)\ge 1-{\epsilon }_i(i=1,2,...,m) \\ {\epsilon }_i\ge 0(i=1,2,...,m) \\ C为自定义超参数 \end{gathered}$$
通过拉格朗日函数构造目标函数：
$$L(w,b,\epsilon ,\alpha ,\mu )=\frac{1}{2}||w|{|}_2^2+C\sum _{i=1}^m{\epsilon }_i-\sum _{i=1}^m{a}_i[y_i(w^T{x}_i+b)-1+{\epsilon }_i]-\sum _{i=1}^m{\mu }_i{\epsilon }_i$$
其中${\alpha }_i\ge 0;{\mu }_i\ge 0$

优化原始问题
$$\underset{w,b,\epsilon }{\min }\underset{{\alpha }_i\ge 0;{\mu }_i\ge 0}{\max }L(w,b,\epsilon ,\alpha ,\mu )$$
对偶问题
$$\underset{{\alpha }_i\ge 0;{\mu }_i\ge 0}{\max }\underset{w,b,\epsilon }{\min }L(w,b,\epsilon ,\alpha ,\mu )$$
依旧是先求极小，再求极大。
$$\begin{gathered} \frac{\partial L}{\partial w}=0\to w=\sum _{i=1}^m{a}_i{x}_i{y}_i \\ \frac{\partial L}{\partial b}=0\to \sum _{i=1}^m{a}_i{y}_i=0 \\ \frac{\partial L}{\partial \epsilon }=0\to C-{\alpha }_i-{\mu }_i=0\to C={\alpha }_i+{\mu }_i \end{gathered}$$
带回拉格朗日函数
$$\begin{gathered} =\frac{1}{2}||w|{|}_2^2+C\sum _{i=1}^m{\epsilon }_i-\sum _{i=1}^m{\alpha }_i[y_i(w^T{x}_i+b)-1+{\epsilon }_i]-\sum _{i=1}^m{\mu }_i{\epsilon }_i \\ =\frac{1}{2}||w|{|}_2^2-\sum _{i=1}^m{\alpha }_i[y_i(w^T{x}_i+b)-1+{\epsilon }_i]+\sum _{i=1}^m{\alpha }_i{\epsilon }_i \\ =\frac{1}{2}||w|{|}_2^2-\sum _{i=1}^m{\alpha }_i[y_i(w^T{x}_i+b)-1] \\ 和硬间隔的形式一致! \\ =-\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{y}_i{x}_i^T{\alpha }_j{y}_j{x}_j+\sum _{i=1}^m{\alpha }_i \end{gathered}$$
通过数学求解，最后得到的求极大形式为：
$$\begin{gathered} \underset{a}{\max }-\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j(x_i\cdot x_j)+\sum _{i=1}^m{\alpha }_i \\ s.t.\sum _{i=1}^m{a}_i{y}_i=0 \\ {a}_i\ge 0;{\mu }_i\ge 0i=1,2,...,m \\ C={\alpha }_i+{\mu }_i \end{gathered}$$
虽然形式一样吗，但是限制条件是不同的！

我们对限制条件再进行优化得到
$$\begin{gathered} \underset{a}{\min }\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j(x_i\cdot x_j)-\sum _{i=1}^m{\alpha }_i \\ s.t.\sum _{i=1}^m{a}_i{y}_i=0 \\ 0\le a_i\le C; \end{gathered}$$
与之前相比，只是多了一个约束条件，仍然可以使用SMO进行求解。

结论：
$$\begin{gathered} {\alpha }_i=0\to 该点为分类正确的点 \\ 0<{\alpha }_i<C\to 该点为软边界上的点 \\ {\alpha }_i=C\to 该点嵌入了软边界内: \\ 如果此时\epsilon <1,该点被分类正确 \\ 如果此时\epsilon =1,该点刚好落在超平面上 \\ 如果此时\epsilon >1,该点被分类错误 \end{gathered}$$

训练流程总结：

1.原始目标：求一组$w,b$使得分隔最大

2.转换目标：利用拉格朗日函数构建目标函数，并分析得到${\alpha }^{\ast }和b^{\ast }和w^{\ast }$之间的关系。
$$\begin{gathered} \underset{a}{\min }\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j(x_i\cdot x_j)-\sum _{i=1}^m{\alpha }_i \\ s.t.\sum _{i=1}^m{a}_i{y}_i=0 \\ 0\le a_i\le C; \end{gathered}$$
3.利用SMO算法求得m个$a^{\ast }$

4.利用求得的$a^{\ast }$得到$w^{\ast }$和$b^{\ast }$
$$\begin{gathered} w^{\ast }=\sum _{i=1}^m{a}_i^{\ast }{y}_i{x}_i \\ {b}_s^{\ast }=y_s-\sum _{i=1}^m{a}_i^{\ast }{y}_i{x}_i^T{x}_s \\ {b}^{\ast }=\frac{1}{S}\sum _{i=1}^S{b}_s^{\ast } \end{gathered}$$

3.非线性支持向量机：

判别函数的另一种表现形式

对于线性SVM来说，判别函数为$y=(w^{\ast T}x+b^{\ast })$

由于$w^{\ast }={\sum }_{i=1}^m{a}_i^{\ast }{y}_i{x}_i$,所有也有下面这种判别函数的形式：
$$y=(\sum _{i=1}^m{a}_i^{\ast }{y}_i(x_i\cdot x))+b^{\ast }$$

如何处理线性不可分问题

升维是一种处理线性不可分问题的方式，我们通过把原始的X映射到高维空间$\phi (x)$上，比如多项式回归：

可以将2元特征（x1,x2）映射为5元特征$x_1,x_2,x_1\ast x_2,x_1^2,x_2^2$这样在五元空间中有些二元空间里线性不可分的问题就变得线性可分了

将这个思想引入SVM，可以处理线性不可分的问题

但是看似这样的升维方式已经完美解决了线性不可分问题，但是带来了一个新问题，假设就使用多项式回归的方式进行升维：对于二维$x_1,x_2$升维后的结果是：$x_1,x_2,x_1\ast x_2,x_1^2,x_2^2$

假如是三维数据，思维数据等更高维呢?$x_1,x_2,...,x_n$

这样会产生维度爆炸的问题。

因此在SVM中引入核函数解决这一问题

升维（核函数）：

在SVM学习过程中
$$\begin{gathered} \underset{a}{\min }\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j(\varphi (x_i)\cdot \varphi (x_j))-\sum _{i=1}^m{\alpha }_i \\ s.t.\sum _{i=1}^m{a}_i{y}_i=0 \\ 0\le a_i\le C; \end{gathered}$$
我们只需要求得$\varphi (x_i)\cdot \varphi (x_j)$的结果，并不需要知道具体的$\varphi (x)$是什么。于是决定跳过$\varphi (x)$直接定义$\varphi (x_i)\cdot \varphi (x_j)$的结果，这样既可以达到升维ied效果，又可以避免维度爆炸的问题。

因此定义核函数：
$$K(x,z)=\varphi (x)\cdot \varphi (z)$$
此时，目标函数就变为：
$$\begin{gathered} \underset{a}{\min }\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_{j}K(x_i,x_j)-\sum _{i=1}^m{\alpha }_i \\ s.t.\sum _{i=1}^m{a}_i{y}_i=0 \\ 0\le a_i\le C; \end{gathered}$$
判别函数就为：
$$y=(\sum _{i=1}^m{a}_i^{\ast }{y}_{i}K(x_i,x))+b^{\ast }$$

常用的核函数：

1.线性核函数
$$K(x,z)=x\cdot z$$
2.多项式核函数
$$K(x,z)=(\gamma x\cdot z+r{)}^d$$
3.高斯核函数
$$K(x,z)=exp(-\gamma ||x-z|{|}^2)$$
4.Sigmoid核函数
$$K(x,z)=tanh(\gamma x\cdot z+r)$$

SVM算法流程总结

1.选择某个核函数以及其对应的超参数

2.选择惩罚系数C

3.利用拉格朗日函数构造最优化问题

4.利用SMO算法求解出一组${\alpha }^{\ast }$

5.根据${\alpha }^{\ast }$计算$w^{\ast }$

6.根据${\alpha }^{\ast }$找出全部支持向量，计算每个支持向量对应的$b_s^{\ast }$

7.对$b_s^{\ast }$求均值得到最后的$b^{\ast }$

8.学习得到超平面为：
$$\sum _{i=1}^m{a}_i^{\ast }{y}_{i}K(x_i,x)+b^{\ast }=0$$
9.最终的判别函数为：
$$f(x)=sign(\sum _{i=1}^m{a}_i^{\ast }{y}_{i}K(x_i,x)+b^{\ast })$$

Sklearn中使用SVM

最基本用法：

from sklearn import svm
#训练
clf = svm.SVC()
clf.fit(X, y)
#预测
clf.predict([[2., 2.]])
#获得支持向量
clf.support_vectors_
#支持向量的索引
clf.support_
#获取每个类中支持向量的个数
clf.n_support_

其他用法使用时查就可以了

1.4 支持向量机-scikit-learn中文社区