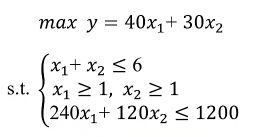数学建模准备知识
比赛时间一般为每年9月,提交的材料MD5生成之后,就不要再碰了,不要打开。
看视频建议:
- 学习算法的过程,只要明白算法的优缺点,适用范围,知道每种算法到底可以干什么就可以了,以及如何实现。
- 看优秀论文,了解解题思路,看到某题就可以马上想到用那种方法
1 百度技巧
- 加双引号”“,进行完全匹配
- 标题必含关键词:查询前加上intitle
- 搜索文档:查询词后 空格 再输入filetype:文件格式(doc/pdf/xls等等)
- 去掉不想要的:查询词后面加空格后加减号与关键字
例如:线性规划 filetype:pdf -百度文库
2 知网查询技巧
先看知网的硕博论文,按照”被引“排序,看背景介绍,利用好高级检索。
对于数模国赛,没必要查外文文献
3 去那找数据
- 优先在知网、谷歌学术等平台搜索
- 国家统计局:最全面,月度季度年度,各地区各部门各行业
国家数据 (stats.gov.cn)![]() https://data.stats.gov.cn/
https://data.stats.gov.cn/
- EPSDATA平台:具有丰富的数据资源和大量分析处理过的数据结果,是收费的,不过可以申请7天的试用 EPSDATA官网 (epsnet.com.cn)
 https://www.epsnet.com.cn/index.html#/Index
https://www.epsnet.com.cn/index.html#/Index
3.1 数据预处理
缺失值
- 比赛提供的数据,发现有些单元格是NULL或空的
- 缺失太多,例如调查人口信息,发现”年龄“这一项缺失了40%。就直接把该项指标删除
- 最简单的处理:取均值进行代替,采用众数插补
- Newton插值法
- 根据固定公式,构造近似函数,补上缺失值,普遍适用性强
- 缺点:区间边缘处的不稳定震荡,即龙格现象,不使用对导师有要求的题目。
- 适用赛题:热力学温度、地形测量、定位等只追求函数值精准而不关心变化的数据
- 样条插值法
- 用分段光滑的曲线去插值,光滑意味着曲线不仅连续,还要有连续的曲率
- 适用赛题:零件加工,水库水流量,图像”基线漂移“,机器人轨迹等精度要求高、没有突变的数据
异常值
- 样本中明显和其他数值差异很大的数据,例如一群人的升高数据中有个3米2的
- 正态分布3σ原则
- 求解步骤:1.计算均值u和标准差σ;2.判断每个数据值是否在(u-3σ,u+3σ)内,不在则为异常值。
- 适用题目:总体符合正态分布,例如人口数据、测量误差、生产加工质量、考试成绩
- 不使用的题目:总体符合其他分布,例如公交站人数排队,符合泊松分布
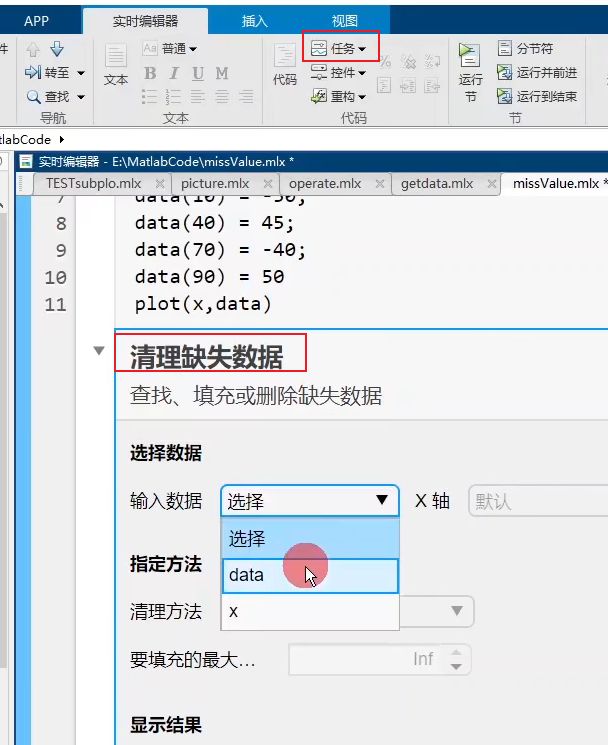
MATLAB异常值处理方法:
创建****.mlx 实时代码文件,高版本才有这个选项
4 建模全过程
- 一篇完整的数模论文
- 包括摘要(最重要),问题重述、模型假设和符号说明、模型建立与求解(内容最多)、模型的优缺点与改进方法、参考文献和附录。
- 摘要:论文研究的问题、用了什么方法、求得了什么结果,以及每一部分得大致步骤。
- 问题重述
- 将题目简述一遍即可,并不重要。注意不要复制粘贴,避免查重。
- 模型假设和符号说明
- 好的假设可以事半功倍
- 符号说明:将论文中定义得重要符号列出表格说明即可。
模型得建立:
- 一组公式,对公式中每个变量得解释,就是一个模型
- 先查阅资料,看着资料,用自己得话复述一个简单的模型,再根据题目中的约束条件去一步步修改模型,把题目中的变量代入模型中。
- 模型求解
- 并不是针对题目的每一个问题都要建立一个模型
- 模型的优缺点与改进方法:这一部分不是必须的,可以简单分析下前文模型的优缺点,若没有改进的方法也可不屑
- 结合查到的文献,分析正文中模型常用在那种问题,又与本文所求解的问题有何区别
附录:正文中求解时用到的代码,注意把查到的代码里变量名换一换,避免被查重
5 论文排版注意事项
各级标题与正文层次分明,不要出现大片空白,一般标题级别不超过3级,正文中文字为宋体,英文Times New Roman,表格采用标准的三线表。
6 标题怎么写
读完标题,就能知道本文建的是什么模型。简明扼要、符合规范、便于检索,尽量使用大家都知道的词语。
基于***模型/算法的***问题研究
- ***模型就是正文里的核心模型
- ***问题就是赛题的中心词
- 不要使用过多的修饰词
7 摘要如何写
让评阅老师读完摘要后,就知道本文解决的问题、建立的模型和求解结果。控制在3/4~1页。字数800~1100。
开头段模板:本文主要研究了***问题。根据***,利用***模型/方法,求解出****。
- 第一句:说明研究的问题
- 第二句:说清全文采用的模型/算法、采取的操作
- 开头段不要写详细的求解结果。
中间段模板:针对问题一,考虑/根据***,...,建立***模型/利用****方法,....求解出****。一定要写清楚结果。
- 优化类、预测类和物理类的题目,要明确写清数值。
- 要求提供建议或评价的题目,明确写清结论和数据依据,但不要有表格,数据过多可说明数据见附录。
总结段:如果写完后摘要超过一页了,可以不写,不要累赘重复前面写过的内容,写一些本文的特色、自夸的语句。
关键词:一般为4~6个,使用的模型和算法,大家都知道的专业名称,问题的关键词,中间以空格分开
8 参考文献
引用文献或公开资料都必须按规范列出参考文献并在正文对应处标注。
9 作图技巧
注意排版,无首行缩进,居中对齐。
常见作图软件:AxGlyph、MATLAB,万能神器EChartsApache ECharts![]() https://echarts.apache.org/zh/index.html
https://echarts.apache.org/zh/index.html
10 巧用分页符
摘要单独占一页,摘要后插一个分页符。注意分页符和分节符的区别,一般用不到分节符,主要用分页符。
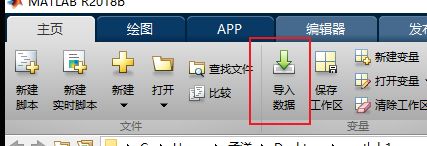
11 MATLAB如何导入数据
第一中方法:利用CTRL键选择需要导入的数据。以表的方式导出
第二种方法:
horse_data = xlsread('E:\文件位置\new_data.xlsx','sheet1'); % 导入表格数据
horse_1 = horse_data(1,:); % 导入第一行数据12 线性规划
线性规划:所有变量都是一次方。
适用赛题:
- 题目中提到 如何分配/安排 尽量多(少) 最多(少) 利润最大 最合理 等词。
- 生产安排:原材料、设备有限制,总利润最大
- 投资收益:资产配置、收益率、损失率、组合投资、总收益最大
- 销售运输:产地、销地、产量、销量、运费、总运费最省
- 车辆安排:路线、起点终点、承载量、时间点、车次安排最合理
有限的条件下,最大的收益,s.t.表示约束条件,设置的参数x1 x2 即为决策变量,max为目标函数
MATLAB实现:Linprog函数
- 把模型化为matlab标准型:目标函数最小值、约束条件<=或=
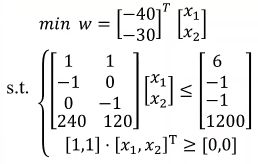
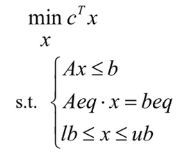
- [x, fval] = linprog(c, A, b, Aeq, beq, lb, ub)
c 目标函数系数的列向量 a, b 不等式约束条件的变量系数矩阵和参数项矩阵 aeq, beq 等式约束条件的系数矩阵和常数项矩阵 lb, ub 决策变量的最小取值和最大取值
x 返回最优解的变量取值
fval 返回目标函数的最优值
- 若不存在不等式约束,用 [] 代替A和b [x, fval] = linprog(c, [], [], Aeq, beq, lb, ub)
- 若不存在等式约束,用 [] 代替Aeq, beq [x, fval] = linprog(c, A, b,[], [], lb, ub)
- 没有等式约束和最小、最大取值的约束时,可以不写Aeq, beq, lb, ub [x, fval] = linprog(c, A, b)
- 若题目求最大值:目标函数等号两端加负号转为求最小值,求解后目标值再取负。
c = [-40; -30]; % 注意写成列向量
a = [1 1; -1 0; 0 -1; 240 120];
b = [6; -1; -1; 1200];
% 因为在约束条件a中,已经写了x1 x2 的范围,所以没必要再写lb,ub了
[x, y] = linprog(c, a, b);
y = -y;13 非线性规划
有限的条件下,求最大的收益
非线性规划:至少一个变量不是一次方,涉及到三角函数的
适合赛题:例如角度调整,飞行管理避免相撞,影院最佳视角。
14 多目标规划问题
既要****,又要*****
- 例如,目标1是“不超过”,也就是尽量≤;目标2是 充分利用,也就是尽量 = ,目标3是不少于,也就是≥
- 需要衡量每个目标的完成情况,并主观上区分三个目标的重要性,使得整体的完成情况尽量好。
- 绝对约束:模型中自带的约束条件,必须满足,否则是不可行解
- 目标约束:模型中对不等式右端追求的值允许有偏差
- 优先因子:确定目标的重要性
求解方法:搜索MATLAB的fgoalattain函数,或序贯算法,或用Lingo求解
15 最短路径问题
最短路径:从图中的某个点出发,到达另外一个顶点的所经过的边的权重之和最小的一条路径。
图:边和节点组成的结构,分为有向图和无向图
权重:道路的长度
MATLAB求解最短路径:Dijkstra算法,或MATLAB的graphshortestpath函数
第一步:生成邻接矩阵
W = [10,5,2,1,4,6,7,3,9,2]; % 每条边的权值
% sparse生成稀疏矩阵,也就是除了注明的几个元素外,其余都是0
% sparse里第一个和第二个矩阵相同位置的元素值就是 从*到*的方向,对应W里的权值
DG = sparse([],[],W) % DG为生成的邻接矩阵第二步,生成图对象,求解最短路径
% dist是最短路径的值,path是最短路径的节点顺序
% pred是到每一个节点的最短路径的终点前一个节点,一般用不到
% 1 代表起始节点,3 代表目标节点,即1到3的最短路径
[dist,path,pred] = graphshortestpath(DG,1,3);
% biograph生成图对象,view显示该图
point_name = ["节点1","节点2","节点3","节点4"];
h = view(biograph(DG,point_name,'ShowWeights','on')) % 后两个参数为显示路径长度% 将最短路径的节点和边缘标记为红色并增加线宽
% getedgesbynodeid得到图h的指定边的句柄
% 第一个参数为图,第二个是边的出点,第三个是边的入点
% 句柄确保能找到对应的东西
% get查询图的属性,h.Nodes(path),'ID'得到图h中最短路径的边
% set设置图形属性
edges = getedgesbyodeid(h,get(h.Nodes(path),'ID'));
set(edges,'LineColor',[1 0 0]); % R G B
set(edges,'LineWidth',2);注:节点标签和字体大小也可以进行修改,通过getedgesbyodeid函数获取相关信息,再进行set
16 最小生成树
连通所有顶点且总路径最小。
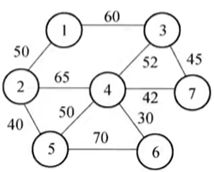
例:修建连通7个城市的铁路网,可修建的路线和对应造价如图所示,如何修建能使得总费用最少。
问题分析:
- 连通7个城市:生成的图中,从任意顶点起步,沿着边一定可以到达所有的其他顶点,这种图叫做连通图。
- 可修建的路线和对应造价:图的边,及其权值
- 总费用最少:权值之和最少
- 和最短路径的区别:最短路径是针对某一顶点作为起点而言的,最小生成树是所有顶点连通且总路径最小。
% 前两个矩阵对应节点,主要无向图写的时候避免重复,技巧第2个矩阵写比第一个矩阵大的节点
s = [1 1 2 2 3 3 4 4 4 5];
t = [2 3 4 5 4 7 5 6 7 6];
wights = [50,60,65,40,52,45,50,30,42,70];
% 生成无向图,wights是对应的权值
G = graph(s,t,weights);
% 求出最小生成树,得到的T包含最小生成树的节点和对应边的权值
T = minspantree(G);
% p = plot(G)就能把图片展现出来,后面是为了美观设置字体
p = plot(G,'EdgeLabel',G.Edges.Weight,'MarkerSize',8,'NodeFontSize',16,'EdgeFont',4)
% 突出显示绘制的图中的节点和边
highlight(p,T,'EdgeColor','red','LineWidth',3) 最小生成树的求解
1.利用MATLAB的minspantree函数求解最小生成树,见上面的程序
2.Kruskal算法:适合点多边少的图
3.Prim算法:适合边多点少的图
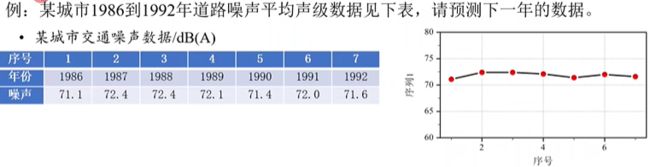
17 灰色预测GM(1,1)模型
GM(1,1)模型:1阶微分方程,1个变量
特点:数据少,看不出明显规律,适合用灰色预测
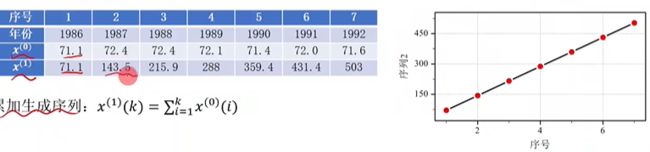
看不出规律,采用累加的方法制造规律。
生成的新序列,一般看起来像一个指数曲线(直线)
- 可以用一个指数曲线乃至一条直线的表达式来逼近这个新序列
- 构建一阶常微分方程来求解拟合曲线的函数表达式
优点:数据少且无明显规律时可用,利用微分方程挖掘数据本质规律
缺点:灰色预测只适合短期预测、指数增长的预测