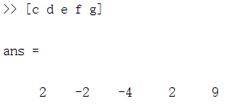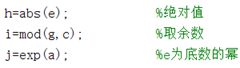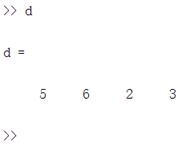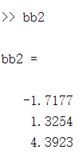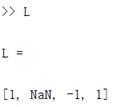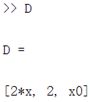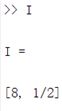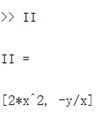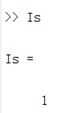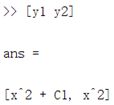MATLAB入门实战版
写在前面
众所周知,MATLAB是理工科不可不知的利器,其功能之广、之强可谓万金油。其在科研、数模竞赛、课设等当中有着广泛的用途,甚至也有地方专门开了MATLAB的相关课程。学习MATLAB,对于非计算机专业的理工科选手而言还是很有用的。
MATLAB的学习,也并不是过于复杂的,尤其是对于有编程基础的人而言。这里,我从多个方面入手,用一些比较基础的例子,来讲解MATLAB的m语言编程和simulink仿真中的多个问题。不过这里讲的比较浅,深入的建议参考一些相关的好书,如《MATLAB从入门到精通》等等。
当然,MATLAB的学习,仅靠看是不够的,最好的方法是一边看着资料,另一边也打开MATLAB进行实际操作,毕竟MATLAB是一种工具——只有自己动手去使用才能真正学会。此外MATLAB也博大精深、易学难精,入坑以后,慢慢探索吧。
此外,由于本人水平有限,以及该资料主要针对新手,如有觉得过于简单者,请不要介意。
目录
上篇 M语言编程
PART I 基础算术
PART II 程序设计
PART III 矩阵运算
PART IV 基础画图
PART V 图像处理
PART VI 高等数学
下篇 Simulink仿真
PART I 信号仿真
PART II 纯电路仿真
PART III 综合仿真
上篇 M语言编程
PART I 基础算术
MATLAB里的算术类似于很多常见编程语言,但是语法结构较简单一些,并存在一些内置函数,这里简单举例说明。
(1)首先是简单的清理和赋值,其中赋值只需要直接“a=1”,无需类型。语句需要分号结束(这里用python的注意一下)。
图1
(2)接下来是简单的加减乘除四则运算和乘方运算,乘方处的例子涉及到“()”的使用。
图2
图3
(3)当然MATLAB里还有其他一些算术方面的内置函数,这里以绝对值(模)、余数、自然对数为例。这些仅仅是一小部分,如需更深入了解,可参考《MATLAB》从入门到精通。
图4
图5
脚本代码
clc,clear %命令行窗口、工作界面清除功能
a=1;b=1; %数据定义
c=a+b; %算术加
d=a-3; %算术减
e=c*d; %算术乘
f=e/(-c); %算术除
g=(c+b)^2; %算术乘方
h=abs(e); %绝对值
i=mod(g,c); %取余数
j=exp(a); %e为底数的幂PART II 程序设计
MATLAB中,程序设计部分内容较多,也类似于我们学过的编程课中所提到的,包括定义函数、条件结构、循环结构等内容。当然,这里只涉及其中一小部分典型的方法。
(1)函数定义,只需从左上角的加号新建函数即可。用function定义函数,n为自变量,a为因变量,Fac为函数名(多个变量要用逗号隔开),这里定义一个阶乘函数。其内容为n如何得到a即可,末尾要有end(完整性)。另外我这里的辅助变量L,是一种在有些情况比较好用的一种思路,即用变量对应值对应条件的一种情况,对该思路有兴趣的可以适当了解。
图1
(2)函数内部,这里是if条件结构和for循环结构。If条件结构又可分为仅有if的结构和if&else结构,一个结构只需一个end(if和elseif/else共用一个end),以此筛选掉不适用的数,并计算0!=1。下面的for循环中,i=1:n则为i从1开始逐次加1加到n,用此逐次计算阶乘即可。
图2
(3)然后可以设置各种运行结果,这里以设置错误、警告情况为例。对之前筛选出的情况,我们直接用error生成错误结果。此外,一定条件我们也可以用warning进行警告,当然此时是可以运行的。
图3
(4)新建脚本,代入函数,a分别设为4(对应图6)、6(对应图7)、1.5(对应图8)、-3(对应图8)、0(对应图9)、1(对应图10、图11),观察结果。
![]()
图5
图6
图7
图8
图9
图10
图11
脚本代码
clc,clear
a=4;
b=Fac(a); %调用函数函数代码
function [a] = Fac(n) %函数定义
L=0; %可以设一个辅助变量表示一种情况
%此处为函数如何实现
if mod(n,1)==0 %if结构
L=1;
if n<0 %if&else结构
L=0;
elseif n==0
a=1;
else
a=L;
for i=1:n %for循环
a=a*i;
end
end
end
if L==0
error('输入不规范'); %出错
elseif n==1
warning('太简单我看不起');%警告
end
endPART III 矩阵运算
MATLAB中m语言的核心,实为通过分析矩阵解决问题。这些矩阵中,向量(一行或一列的矩阵)既基础又重要。这里则简要地讲讲向量和其他矩阵的定义和运算。
(1)向量定义中,先讲行向量,有三种典型的定义方法,如图所示即可,a1为最基本的列举法。当然,后两者a2、a3向量的定义仅限于向量的元素为等差数列的情况,但这也是很常用的情况,在后续的画图中有重要作用。b为列向量,“;”用于将行隔开。
图1
图2
![]()
图3
(2)向量的运算,首先是基本的——向量可与常数进行四则运算,以加法为例得c1。元素个数相同的行、列向量可以直接相乘,如c2,结果为《线性代数》中矩阵乘法的结果。然后c3为矩阵元素的使用案例,直接a1[i]这种格式即可,如果要元素替换也是类似的这种方法。当然这个c3案例实为m语言中“点乘”定义的代码形式,即两个向量/矩阵每个对应元素相乘所得向量/矩阵,当然在实际工程中只需用c4的“.*”即可,类似的还有“./”(右除)、“.\”(左除)、“.^”(点乘方)等。最后提一下,求转置只需“d=b’”即可。
图4
图5
图6
图7
(3)其他非向量矩阵的定义,简单的可以像A这样列举,或者像B这样(“[]”内的“[]”不算错误)。当然,也可以列举已有的向量来定义矩阵。
图8
图9
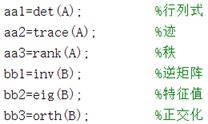
(4)矩阵的运算(线性代数运算)在MATLAB中有很多内置函数,这里举了六个简单的实例。当然这只是冰山一角,还有很多感兴趣可以深入了解。
图10
图11
图12
图13
图14
脚本代码1
clc,clear
a1=[1 3 6 7]; %列举法
a2=1:2:7; %等差数列(首项、公差、末项)
a3=linspace(1,7,4); %等差数列(首项、末项、个数)
b=[5;6;2;3]; %列向量的定义(行由分号隔开)
c1=a1+6; %向量/矩阵与常数的四则运算
c2=a1*b; %向量/矩阵乘法
for i=1:4
c3(i)=a1(i)*a2(i); %向量/矩阵元素的引用
end
c4=a1.*a2; %向量/矩阵点乘
d=b'; %转置脚本代码2
clc,clear
A=[1 0 0;0 2 0;0 0 3];
B=[[1 0 3];[0 2 1];[1 6 1]];
aa1=det(A); %行列式
aa2=trace(A); %迹
aa3=rank(A); %秩
bb1=inv(B); %逆矩阵
bb2=eig(B); %特征值
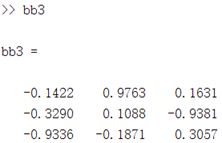
bb3=orth(B); %正交化PART IV 基础画图
MATLAB的画图功能,因其常用性是一个重点。画图有很多种,有二维或三维,具体有线条图形、统计图形、矢量图形、曲面等等。此外,MATLAB画的图,也有各种各样的标注功能。以下,将以多个不同的例子具体介绍。
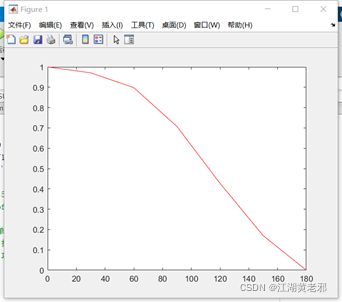
(1)首先定义一个自变量矩阵,这里的自变量为控制角——a;再来一个因变量,为功率因数——pf。有了这之后,直接plot(自变量,因变量,其他)即可画图(单因变量),其他可以注明颜色、形状。当然,“其他”部分的常见情况在三表中列出,同时表示颜色和形状可用‘.c’等格式。
图1
图2
表1
| 颜色 |
红 |
黄 |
绿 |
青 |
蓝 |
紫 |
黑 |
白 |
| 表示 |
r |
y |
g |
c |
b |
m |
k |
w |
表2
| 线型 |
实线 |
虚线 |
点线 |
点画线 |
| 表示 |
- |
-- |
: |
-. |
表3
| 点型 |
加号 |
圆圈 |
星号 |
实点 |
叉 |
菱形 |
正方形 |
| 表示 |
+ |
O |
* |
. |
x |
d |
s |
| 点型 |
五角星 |
六角星 |
向上三角 |
向下三角 |
向左三角 |
向右三角 |
|
| 表示 |
p |
H |
^ |
v |
> |
< |
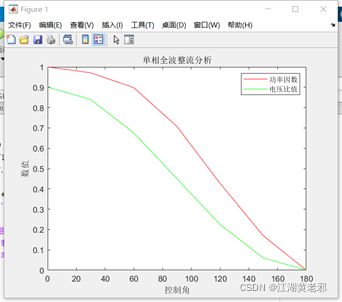
(2)此时由单因变量到多因变量,只需plot(自变量1,因变量1,其他1,自变量2,因变量2,其他2)即可,这里的因变量2为电压比值——vv。
图3
![]()
图4
(3)完成之后可以简单给图加上标注,标题为title(‘标题内容’),坐标为xlabel(‘横坐标内容’)、ylabel(‘纵坐标内容’),多变量时用legend(‘变量1’,‘变量2’)区分变量即可。
图5
图6
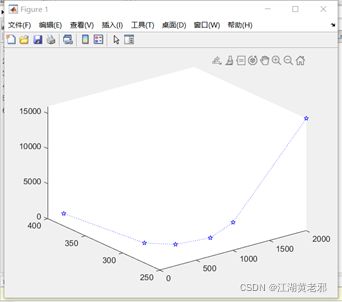
(4)以上为二维折/曲线图现在延伸到三维折/曲线图,只需定义三个向量a1、a2、a3,再使用plot3函数即可,和plot基本类似,为plot3(x,y,z,其他)。当然,如需多线条、标注操作,则类似于(2)(3)的操作在三维方面适当调整即可。
图7
图8
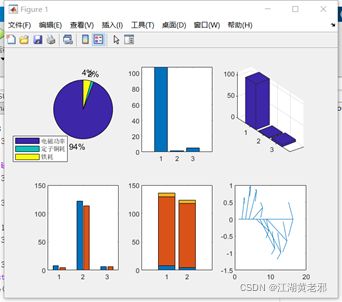
(5)接下来的内容为多图和特殊图形,多图的函数为subplot(行数,列数,第几个),特殊图形中有饼状图、柱状图、矢量图等,各有其对应的函数,如图中所示,直接使用即可。
图9
图10
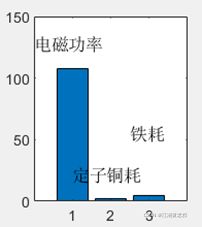
(6)给图加标注的补充内容。坐标限制,用axis([xmin xmax ymin ymax])即可;文字标注,用text(x坐标,y坐标,‘文字内容’)即可。
图11
图12
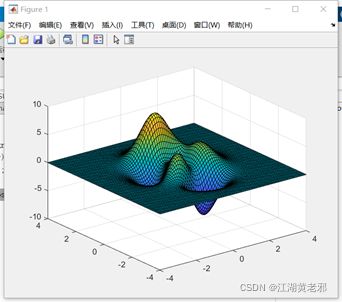
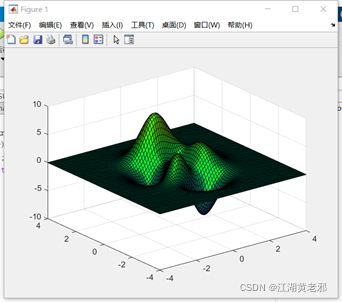
(7)三维曲面图,以山峰为例,先用meshgrid(min:分度:max)定义一个曲面网格,再定义曲面函数(二元),最后使用surf函数画图即可。
![]()
图13
图14
(8)可以再加上灯光,用light函数,里面可以多种设定,如(‘position’,位置坐标)确定灯光方向、(‘color’,颜色)确定灯光颜色等等。
![]()
图15
图16
脚本代码1
clc,clear
a=[0 30 60 90 120 150 180]; %控制角数据
pf=[1 0.971 0.898 0.707 0.427 0.17 0]; %功率因数
%plot(a,pf,'r'); %画图(单线)
vv=(2^0.5)*(1+cos(a*pi/180))/pi; %电压比值
plot(a,pf,'r',a,vv,'g'); %画图(多线)
title('单相全波整流分析'); %标题
xlabel('控制角');ylabel('数值'); %坐标
legend('功率因数','电压比值'); %图例脚本代码2
clc,clear
a=[220 330 500 750 1000 2000]; %x坐标
b=[400 303 278 256 250 250]; %y坐标
c=[121 360 900 2200 4000 16000]; %z坐标
plot3(a,b,c,'b:p'); %三维plot函数脚本代码3
clc,clear
EM=[107.98 1.8 5];
subplot(2,3,1); %多图函数(行数,列数,第几个)
pie(EM); %饼状图
legend('电磁功率','定子铜耗','铁耗');
subplot(2,3,2);
bar(EM); %柱状图
axis([0 4 0 150]); %坐标限制
text(0,127.98,'电磁功率'); %文字标注
text(1,21.8,'定子铜耗');
text(2.5,55,'铁耗');
subplot(2,3,3);
bar3(EM); %三维柱状图
ES=[7.825 122.015 6.493;4.579 113.189 6.023]';
subplot(2,3,4);
bar(ES); %多变量柱状图(横)
subplot(2,3,5);
bar(ES','stack'); %多变量柱状图(竖)
x=linspace(0,2*pi,10);
y=sin(x);
subplot(2,3,6);
feather(x,y); %羽毛图(矢量)脚本代码4
clc,clear
[x,y]=meshgrid(-4:0.1:4); %网格定义
z=peaks(x,y); %曲面函数
surf(x,y,z); %画曲面图
light('position',[-1,-1,1],'color','g'); %调节灯光PART V 图像处理
除了画图,MATLAB也有进行图像处理的能力。对于已有的图像文件,MATLAB可以进行读图、显示、转换成灰度图、拼接、读取图片信息等操作。当然,这些操作与之前不同的是,这回需要现有的图片文件。
(1)这一部分从读图开始,MATLAB可识别的图像文件格式有bmp、jpg、png、pgm等多种格式。先准备一个名为‘eastlake1’的文件,在代码中用‘文件名.文件格式’表示图像文件。用imread(文件)函数读取文件成为矩阵形式,imwrite(矩阵,文件)生成新文件,这一功能可用于改变文件格式等等。
图1
图2
图3
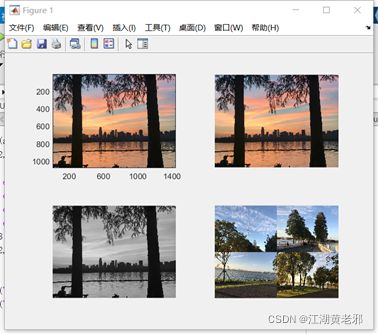
(2)当然图片也可以用于显示于MATLAB的plot结果中(当然不是用plot函数)。用image(矩阵)函数将图片置于坐标系,如不需要坐标系则用imshow(矩阵)。另外,用如果rgb2gray(矩阵)可生成灰度图(黑白灰)。此外,对于矩阵结构相同的图片,可以用矩阵拼接的方法拼图。
图4
图5
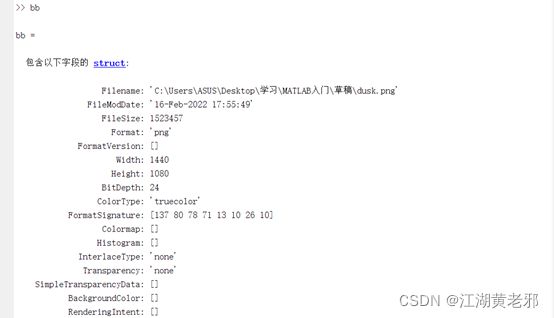
(3)当然,用imfinfo(文件)可以读取文件信息。
图6
图7
图8
图9
脚本代码
clc,clear
a=imread('eastlake1.jpg'); %读取图片文件(矩阵)
imwrite(a,'dusk.png'); %按指定格式生成新的图片文件
subplot(2,2,1);
image(a); %将矩阵以图像形式显示于坐标系
subplot(2,2,2);
imshow(a); %显示图片
b=rgb2gray(a); %生成灰度图
subplot(2,2,3);
imshow(b);
a1=imread('eastlake2.jpg');
a2=imread('eastlake3.jpg');
a3=imread('eastlake4.jpg');
a4=imread('eastlake5.jpg');
A=[a1 a2;a3 a4]; %图片拼接
subplot(2,2,4);
imshow(A);
aa=imfinfo('eastlake1.jpg'); %读取图片信息
bb=imfinfo('dusk.png');PART VI 高等数学
作为一个强大的数学软件,MATLAB自然可以解决很多高等数学中的问题,如极限、求导、积分等。这一应用,也是MATLAB的一个重点,在工程计算和数学建模中较为常见。这里我们举了一些典型的极限、导数、积分、微分方程、级数问题。当然这块内容博大精深,其涉及面之广之深并非可以一时讲清的,建议感兴趣的可以更深入了解。
(1)首先定义一个函数变量x,这种定义需要在前面加上“syms”,有了这之后可以按y=f(x)格式直接定义函数,如这里的f1、f2、f3,或是f4=f(x,x0)。对于求极限,可以用limit(f(x),x,x所趋于的值)求极限。如果用limit(f(x),x,x所趋于的值,‘left’)或limit(f(x),x,x所趋于的值,‘right’)则可求左、右极限。对于求导,可以用diff(f(x),x)直接求一阶导或用diff(f(x),x,n)求n阶导,求偏导亦然。此外,MATLAB中的一些基本数学符号如表中所示。
图1
图2
图3
表1
| 数学概念 |
正无穷 |
负无穷 |
无意义 |
| 表示 |
Inf |
- Inf |
NaN |
(2)当然,MATLAB也可以输入指定函数求各种积分,对于一元积分主要用int函数。定积分和反常积分,直接int(被积函数,下限,上限)即可。要求不定积分时,可以int(被积函数)或int(被积函数,积分变量),后者可用于多元函数。若需要求简单的二重积分,可以按标准格式先定义一个函数名柄,再将其代入integral2(被积函数,x下限,x上限,y下限,y上限)。
图4
图5
图6
图7
(3)微分方程是解决很多数学建模问题的重中之重,MATLAB也是解微分方程的利器。其中,这里以最常见的常微分方程为例介绍。首先定义自变量x和待解函数y(x),对于微分方程f(y(x))=0,列方程的代码格式为:方程名= f(y(x))==0。求解常微分方程的函数为dsolve,求通解只需y1=dsolve(方程名,‘自变量’)即可。若要根据初始得出特解,则需要用y2=dsolve(方程名,‘初始条件’,‘自变量’)。
图8
图9
(4)高等数学还有一个很重要的内容——级数。对于数列前n项和以及无穷级数求和,用函数symsum(通项,自变量(n),1,末项)即可。级数的展开,分为泰勒展开和傅里叶展开。泰勒展开用taylor函数,有多种用法:taylor(f(x))在x=0处展开成六阶,taylor(f(x),‘order’,n)在x=0处展开成n阶,taylor(f(x),x,a,‘order’,n)在x=a处展开成n阶。傅里叶展开我们定义一个Fou函数(这里以区间[0,2π]为例),代入f(x)求出定义即得。
图10
图11
图12
图13
图14
(5)再来讲一讲一个大重点积分变换。傅里叶变换F[f(x)]=F(w)用fourier(f(x))函数求,其逆变换则用函数fourier(F(w))即可;拉普拉斯变换L[f(t)]=F(s)用fourier(f(t))函数求,其逆变换则用函数fourier(F(s))即可。
![]()
图15
图16
脚本代码1
clc,clear
syms x x0; %自变量x的定义
f1=sin(x)/x; %函数定义
L1=limit(f1,x,0); %求极限
f2=abs(x)/x;
L2=limit(f2,x,0);
L3=limit(f2,x,0,'left'); %求左极限
L4=limit(f2,x,0,'right'); %求右极限
f3=x^2;
f4=x*x0;
D1=diff(f3,x); %求导
D2=diff(f3,x,2); %高阶求导
D3=diff(f4,x); %求偏导
L=[L1 L2 L3 L4];
D=[D1 D2 D3];脚本代码2
clc,clear
syms x y;
f1=4*x;
f2=x^(-2);
I1=int(f1,0,2); %求定积分
I2=int(f2,2,inf); %求反常积分
I=[I1 I2];
II1=int(f1); %求不定积分
II2=int(f2*y,x); %对x求不定积分
II=[II1 II2];
f3=@(x,y)(x+y); %定义函数名柄(求二重积分用)
Is=integral2(f3,0,1,0,1); %求二重积分脚本代码3
clc,clear
syms x y(x); %定义x和y(x)
eq=diff(y,x)-2*x==0; %常微分方程
y1=dsolve(eq,'x'); %求通解
y2=dsolve(eq,'y(0)=0','x'); %代条件求特解
脚本代码4
clc,clear
syms n x;
a1=1/n; %数列/级数定义
a2=a1/(n+1);
s1=symsum(a1,n,1,3); %数列求前n项和
s2=symsum(a1,n,1,inf); %无穷级数求和
s3=symsum(a2,n,1,inf);
s=[s1 s2 s3];
g=exp(x);
t1=taylor(g); %x=0处泰勒展开
t2=taylor(g,'order',3); %x=0处控制阶数泰勒展开
t3=taylor(g,x,2,'order',3); %x≠0处控制阶数泰勒展开
h=x^2;
[a0,an,bn]=Fou(h); %展开成傅里叶级数脚本代码5
clc,clear
syms x w t s;
fx1=exp(-x^2);
Fw1=fourier(fx1); %求傅里叶变换
Fw2=exp(-w^2/4);
fx2=ifourier(Fw2); %求傅里叶逆变换
lt1=exp(-2*t);
Ls1=laplace(lt1); %求拉普拉斯变换
Ls2=(s+1)/(s^2+1);
lt2=ilaplace(Ls2); %求拉普拉斯逆变换展开成傅里叶级数函数代码f
unction [a0,an,bn] = Fou(fff)
%在[0,2*pi]展开成傅里叶级数
syms x n;
a0=int(fff,0,2*pi)/pi;
an=int(fff*cos(n*x),0,2*pi)/pi;
bn=int(fff*sin(n*x),0,2*pi)/pi;
end下篇 Simulink仿真
PART I 信号仿真
SIMULINK里的功能为仿真,其基础为信号仿真,需要足够的实践来理解。这里举一个简单的负反馈自动控制系统数学模型仿真全过程的例子,以简要说明其仿真的大致步骤和常用功能。
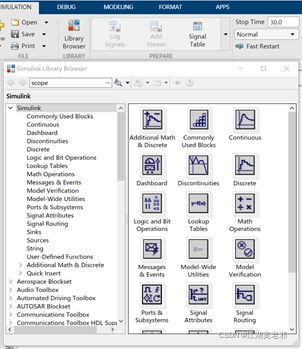
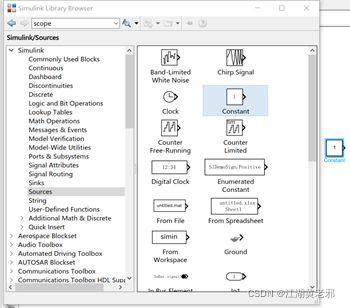
(1)首先要点击library browser(左上角)以打开元件库,里面有各路仿真元件。将第一个simulink栏展开,此处为信号仿真相关元件。
图1
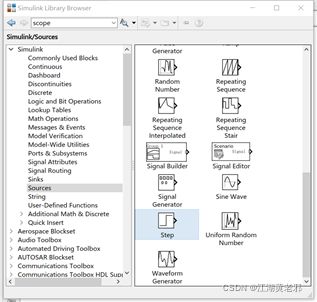
(2)最先放置的为信号源,只需从source栏里挑选即可,如这里所挑选的是单位阶跃信号源。选定后,移至放置区域即可。
图2
(3)接下来放置一些简单的信号处理元件,这里是以continuous里的元件为例,放置两个连续时间信号处理元件。
![]()
图3
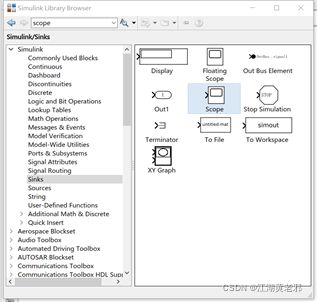
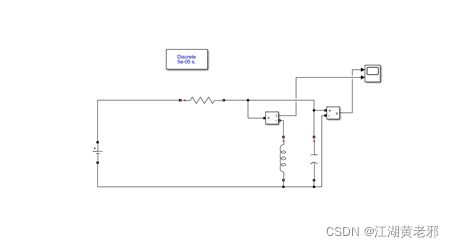
(4)再者从sinks里找出scope即示波器,可以(但不仅限于)用于检测输出信号,一样的放置。放置好后,直接简单用鼠标连接即可,可得到一个用于开环控制的简单的信号处理系统,其传递函数为G1(s)=1/(s(s+1))。
图4
图5
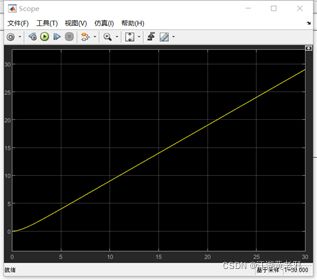
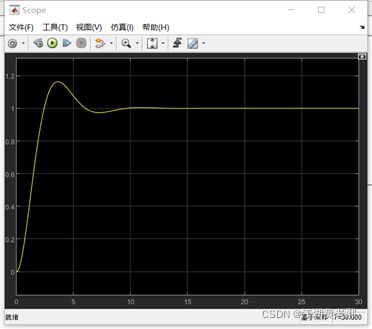
(5)点击绿色run按钮仿真即可,当然刚打开时第一次仿真则需要等待较长时间(尤其如果仿真模型较为复杂的情况)。如果运行成功,则可以直接双击示波器打开以观察波形,其开环传递函数的单位阶跃响应如图所示。
图6
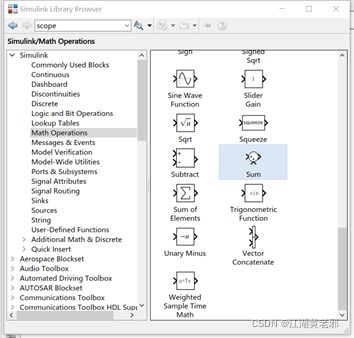
(6)根据《自动控制原理》,为使输出稳定,可以加上负反馈信号。只需打开库中的数学计算元件栏,选择求和元件即可,按图示方式连接起来。当然,这个时候的系统只能算是正反馈控制系统,还尚不能达到输出稳定的效果。
图7
图8
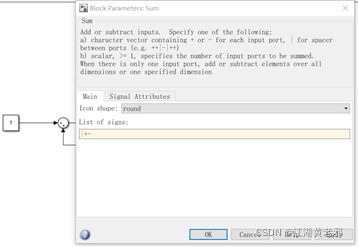
(7)对此,通过调节元件本身性质的方法便可以将正反馈变为负反馈。双击求和元件,将“++”改为“+-”,即得到负反馈效果。此时再运行,得到的信号则为负反馈控制系统的输出信号。(其他各路元件的调整也是双击即可)
图9
图10
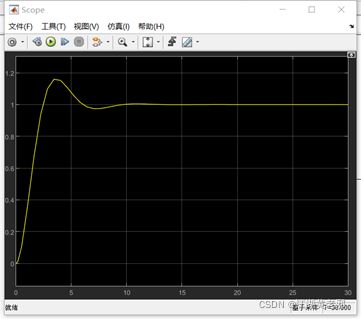
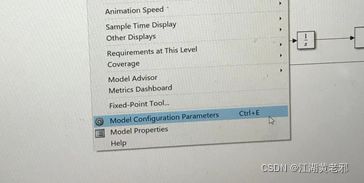
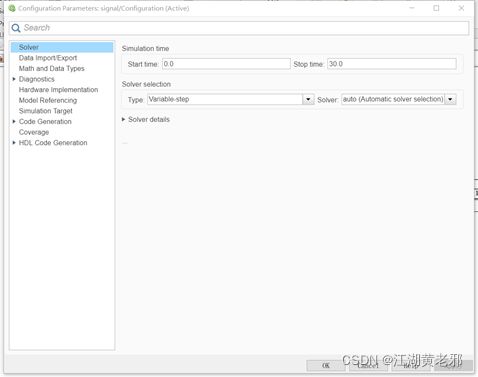
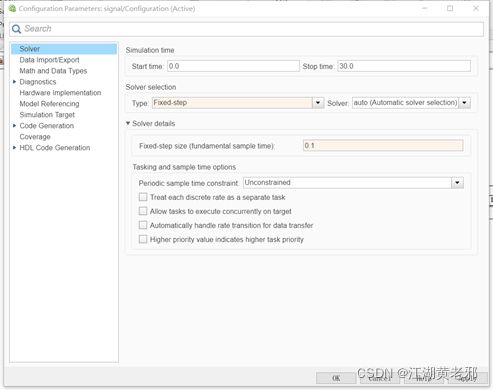
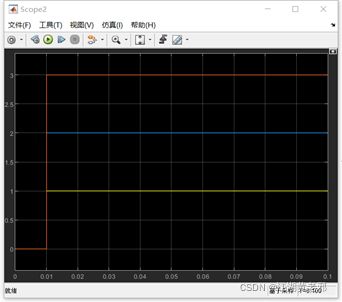
(8)输出信号虽然正确,却不完美,看得出明显的线段,这和采样频率较低是有关的。此时在空白处右键然后点图示按钮,弹出全局设置界面后,于solver处即可调整。其最上面为运行时间,可自行根据需要设置。而我们现在需要的,是把selection改为fixed-step,在details中调整采样时间即可,最终调整后运行结果如图所示,此时图像可谓完美。
图11
图12
图13
图14
PART II 纯电路仿真
SIMULINK也有电路仿真的功能,可以与multisim、psim等其他电路仿真软件进行对比。个人认为,SIMULINK有着较好的电路与信号结合能力以及结合m语言编程的能力,当然这一切的基础除了m语言和信号仿真外,还有纯电路仿真。Simulink有很多电路元件库,本人比较建议按本节步骤使用,随意选择比较容易碰到“黑蓝互斥”这样的情况,这是一个比较麻烦又容易出现的问题。
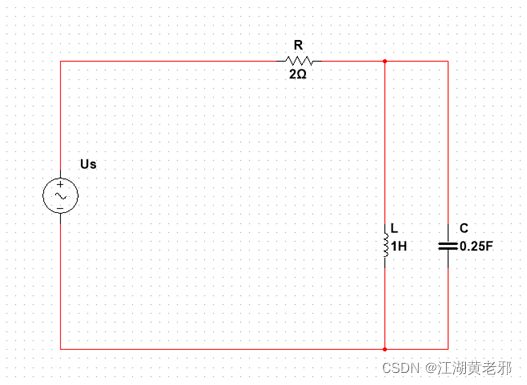
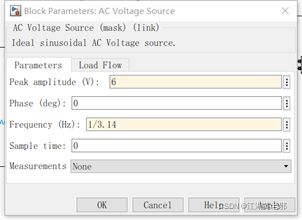
(1)首先我们先设计一个如图所示的电路作为此次仿真的例子(图为用multisim所作)。这里的Us可以为直流和交流电源(考虑图片数量只放一个交流电源的图),给L、C并联再串上一个R的电路,数值如图所示。分别在直流、交流谐振、交流非谐振的情况下测量L上的电流和L、C并联支路上的电压。
图1
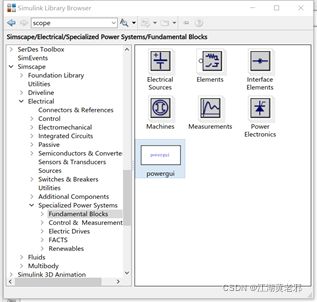
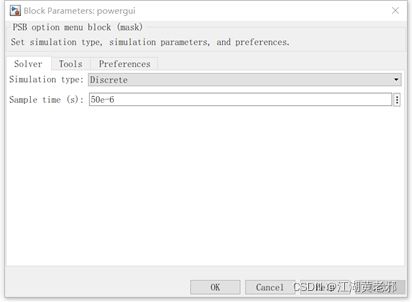
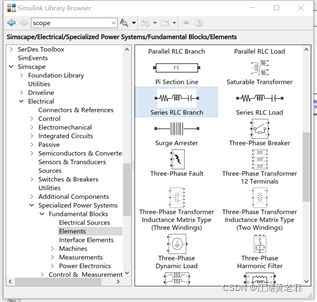
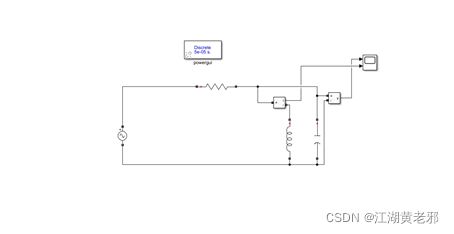
(2)打开元件库,从simscape-electrical-specialized power systems中选取各种电路元件。最先放置的为powergui,放置好后可双击,调成“discrete”(离散)模式(常用),如有需要也可以调整采样时间。
图2
图3
图4
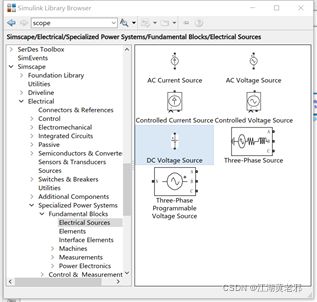
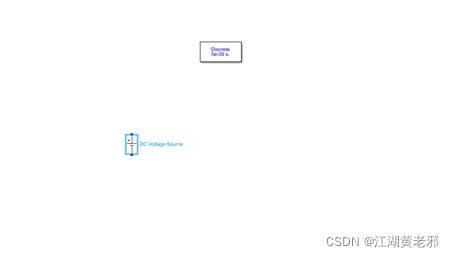
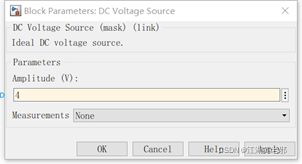
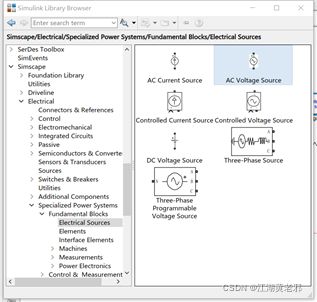
(3)其次为电源,只需从electrical source栏里挑选即可,这里有直流、交流等多种电源。我们先选一个直流电源,然后只需双击设置其电压值即可,这里为4V。
图5
图6
图7
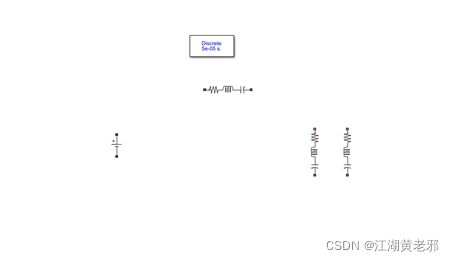
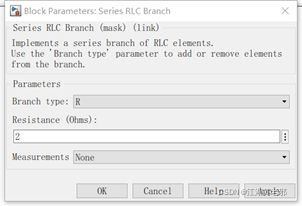
(4)接下来放置一些简单的电路元件——电阻、电容电感,我们直接去elements中取RLC元件来用即可。置于相应位置后,双击打开,根据需要,可设置元件为R、L、C、RL等多种,这里分别为R、L、C,并标上对应的值即可。设置好后,直接连接,便得到了我们需要的电路的拓扑结构。
图8
图9
图10
图11
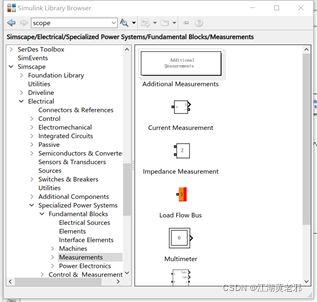
(5)该设置测量部分了,从measurements中取电压、电流测量工具置于相应位置并合理连接即可。其输出端,应当连于示波器scope上。
图12
图13
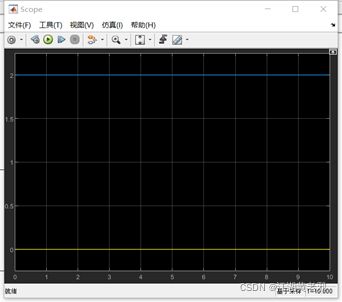
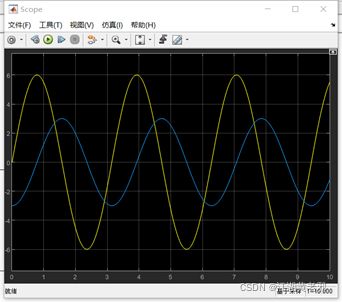
(6)仿真,稳定后打开示波器,此时电压、电流波形如图所示。
图14
(7)我们将直流电源换成交流电压源,调整参数(此时为谐振频率),再次运行,可观察如图所示谐振时的电压、电流波形。
图15
图16
图17
图18
(8)我们还可以调整频率至非谐振状态,再度观察其波形。
图19
图20
PART III 综合仿真
在实际工程中,根据具体情况,SIMULINK的仿真经常要将信号、电路、m语言综合起来。这种综合,既是SIMULINK的一个重要优势,又是SIMULINK学习的一大难点。在本人看来,学习了如何将这些综合起来仿真,才算是学到了MATLAB的精髓。
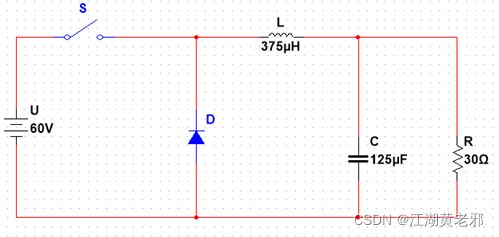
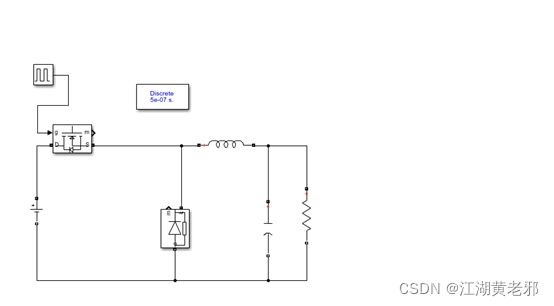
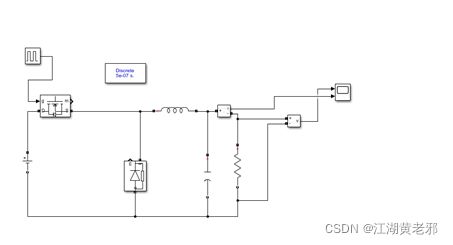
(1)此次仿真的例子以一个开环Buck电路(图为用multisim所作)为基础展开,电路的拓扑结构和参数如图所示。该电路的基本原理为:设电源电压为U,通过占空比为D的PWM波来控制开关S的开合,并结合二极管的续流作用和LC滤波器的滤波作用,使负载R上生成Uo=DU的输出直流电压,实现直流降压功能。该例我们取负载R上的电压、电流为基本测量量。
图1
图2
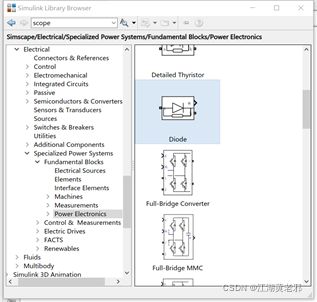
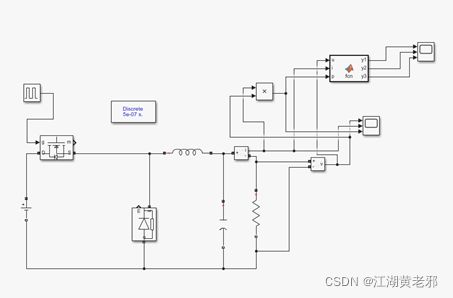
(2)打开元件库,从simscape-electrical-specialized power systems中选取各种电路元件来放置Buck电路的拓扑结构,按以上要求设置元件参数。注意开关管和二极管在power electronics中,常用的开关管可以用mosfet或igbt,这里我们选用mosfet。
图3
图4
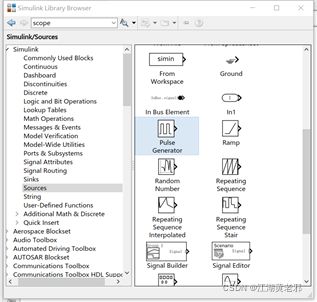
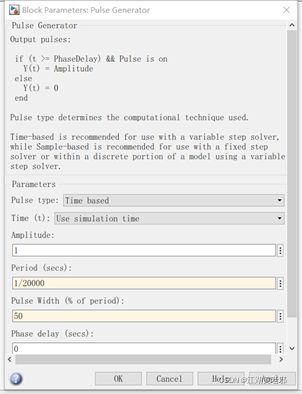
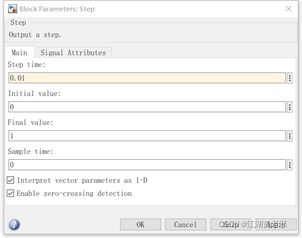
(3)从信号源库中选取方波源给开关管提供PWM,这里将周期调成1/20000s,即频率20kHz。占空比调成50%。
图5
图6
图7
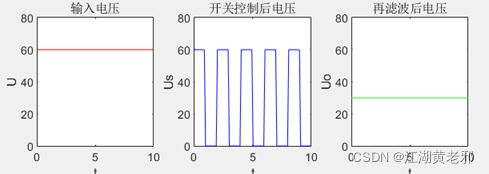
(4)可以设置基本测量部分了,老样子取电压、电流测量工具置于相应位置并合理连接即可,其输出端仍连于示波器scope上。运行,观察波形。考虑到这个例子到后面仿真结构较大,上面的stop time可以从默认的10s调到0.1s(毕竟Buck电路到稳态的时间是很短的)。
图8
图9
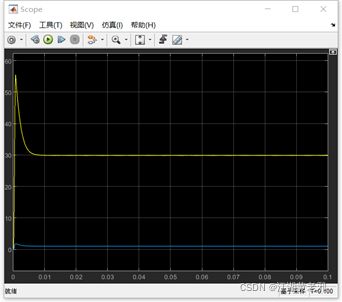
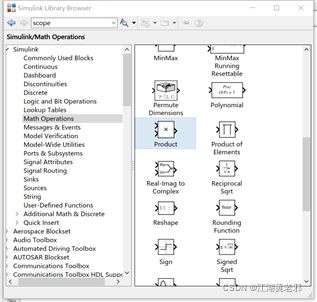
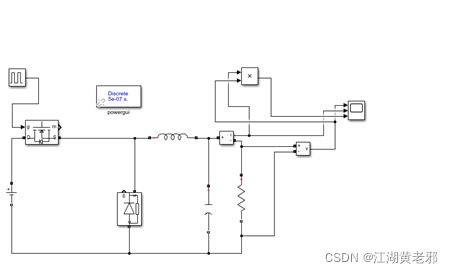
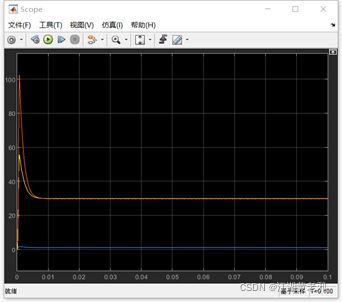
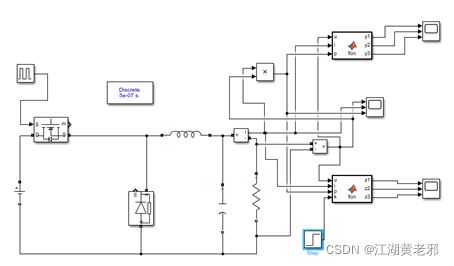
(5)增加测功率部分。取simulink-math operations库中的信号相乘元件,将电压信号和电流信号相乘起来,接至示波器,此时得到负载瞬时功率信号。再仿真,稳定后打开示波器,此时电压、电流、功率波形如图所示。
图10
图11
图12
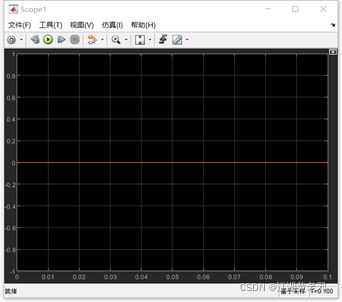
(6)现实中,Buck电路少不了保护措施。对此,我们还可以设置简单的过电压、过电流、过热(功率)保护措施。而保护在瞬时(超调)和稳态中也有不同的要求。先设置瞬时保护,假定瞬时保护临界值分别为60V、2A、120W。我们的方法为:将所测量是否超标转化为易观测的信号,如不超标为零超标则不然,当然这里的三个信号必须区分开来。从simulink-defined functions中选取MATLAB函数放置,双击进入m语言编程,输入为u、i、p,输出为y1、y2、y3。此后,将u、i、p连至电压、电流、功率信号,将y1、y2、y3连于新的示波器。仿真,观察y1、y2、y3信号,正常时为零。此时皆为零,说明安全。
图13
图14
图15
图16
图17
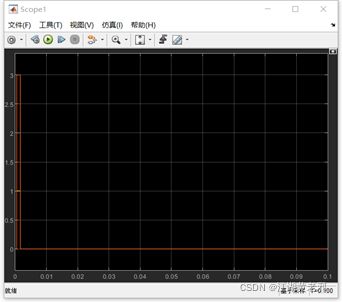
(7)可以把输入电压调至80V再观察该函数的输出值,有一小段时间y1、y2、y3不为零,这便是瞬时保护函数在异常时发出的相应信号。
图18
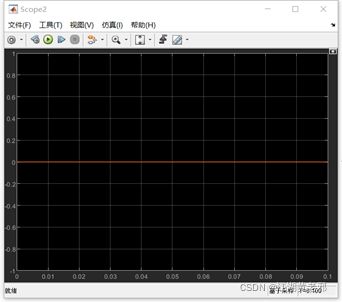
(8)我们还可以加一个稳态保护,假定稳态保护临界值分别为40V、1.2A、50W。先把输入电压U调回60V,再重复刚才的步骤,建立另一个MATLAB函数。为了确保在稳态之后再开始测u、i、p,我在这设了个单位延时阶跃信号源,设置其阶跃时间为0.01s(根据前面的u、i、p的图像可得0.01s后已达稳态),作为除u、i、p外的另一个该函数的输入,并于代码中增加“*k”。此时再运行,观察稳态保护函数对应的示波器上的波形。此时皆为零,说明安全。
图19
图20
图21
![]()
图22
图23
(9)调节输入电压分别为90V,观察该示波器波形。当0.01s后z1、z2、z3持续不为零时,这便是稳态保护函数在对应测量值异常时发出的相应信号。
图24
瞬时保护函数代码
function [y1,y2,y3] = fcn(u,i,p)
y1=0;y2=0;y3=0;
if u>60
y1=1;
end
if i>2
y2=2;
end
if p>120
y3=3;
end稳态保护函数代码
function [z1,z2,z3] = fcn(u,i,p,k)
z1=0;z2=0;z3=0;
if u*k>40
z1=1;
end
if i*k>1.2
z2=2;
end
if p*k>50
z3=3;
end